基于限流电抗器两侧特定频段暂态能量比的MTDC电网单端量保护方案
2024-01-28刘晓军金小东刘迎迎赵冠雄刘亚东
刘晓军,金小东,刘迎迎,赵冠雄,刘亚东
(1.现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林吉林 132012;2.国网潍坊市供电公司,山东潍坊 261100;3.国网长春供电公司,吉林长春 130000;4.国网吉林电力科学研究院,吉林长春 130000)
0 引言
我国于2020 年提出“双碳战略”,未来大量分布式能源会接入电网,清洁能源的不确定性给电网带来了巨大的挑战,采用模块化多电平换流器(Modular Multilevel Converter,MMC)的高压直流(MMC-HVDC)输电技术凭借传输容量大、电能质量高、扩展性强等优势具有广阔的应用前景[1-2],它被越来越多地用于构建大规模多端柔性直流电网[3-4]。
由于柔直线路故障电流上升速度更快,对保护也提出了更高的要求。因此直流线路故障的快速、可靠识别成为柔性直流输电系统发展亟待解决的问题[5-7]。目前,多端柔直线路的保护主要还是以借鉴传统直流保护方法为主。微分欠压过电流保护由于选择性较差,难以满足工程需要。纵联保护可靠性比较高,但由于通信延迟的原因无法满足速动性的要求常被用作后备保护[8]。行波保护受过渡电阻影响较大,但为了限制故障后电流的上升,MTDC 电网中的边界元件已成为不可或缺的部分。
对于直流电网保护,国内外已有大量学者作了相关研究。文献[9]基于Marti 模型,提出行波差动保护方案,但为满足速动性,需严格控制数据窗长度且满足抗干扰能力要求;文献[10]基于VMD 提出纵联保护方案,但需考虑两端通信;文献[11]提出一种基于电流行波的保护方法,通过判断沿线布置相邻电流互感器差值判别区内外故障,该方案投资需投资大量电流互感器,经济性较差;文献[12]基于边界对行波高频分量的衰减作用,使用小波变换的方法提取高频分量识别区内外故障,但理论分析时并未考虑相邻线路边界作用;文献[13]对故障电流的传输路径进行分析,但需加装方向元件且电流行波受过渡电阻影响大;文献[14]构建区内外识别判据和选极判据,但时间窗内数据较短,容易受异常情况干扰。
针对在柔直电网保护中所存在的问题,本文基于现有对多端系统直流线路保护的方案[15],通过对故障电压行波研究。利用不同故障情况下的贝瑞隆等效电路[16],推导出发生区内故障、正向区外故障、反向区外故障时的限流电抗器两侧电压行波特点并定义特定频段暂态能量比。再利用发生区内外故障时限流电抗器两侧特定频段暂态能量比差异性构造保护判据识别故障区域,同时根据不同故障极发生故障时正负极限流电抗器的幅值差进行故障选极。最后利用PSCAD/EMTDC 仿真软件搭建四端直流电网模型,通过仿真验证了所提方法的有效性。
1 基于故障首行波柔性直流电网故障分析
1.1 柔性直流电网拓扑结构
本文基于张北直流电网搭建了±500 kV 的四端柔性直流(柔直)电网,采用对称双极接线方式,主要元件包括交流电源(S1-S4)、换流站(A-D)、限流电抗器(LAB,LBA,LAC,LCA,LCD,LDC,LBD,LDB)、断路器(CB1-CB8)、量测装置(RAB,RBA,RAC,RCA,RBA,RCD,RDC,RBD,RDB)和传输线路(L1-L4),换流站为半桥型MMC,换流站A,B,C 采用定有功功率控制,换流站D 采用定直流电压控制,限流电抗器均配置在换流站出口处,电抗值均设置为150 mH,图1 中F1-F11分别为设置的不同位置的故障点。
1.2 故障特性分析
1.2.1 正向故障
基于本文研究的四端柔直电网拓扑结构,通过Karrenbauer 变换将其解耦并在线模网络中分析求解,线路区内故障与区内末端故障的等效电路如图2(a)和(b)所示。正向区外故障等效电路如图2(c)所示。图2 中的Uf1(jω)为故障等效电源,Rf为故障等效过渡电阻,BAB1,BfA1,BfB1为贝瑞隆模型等效电源,IR1(jω),If1(jω)分别为频域内断路器位置电流与故障位置等效电流,ZmA,ZmB分别为换流器A 与B 的等效阻抗,ZC1为线路等效阻抗,Ub1(jω)与UL1(jω)分别为限流电抗器母线侧与线路侧的电压。
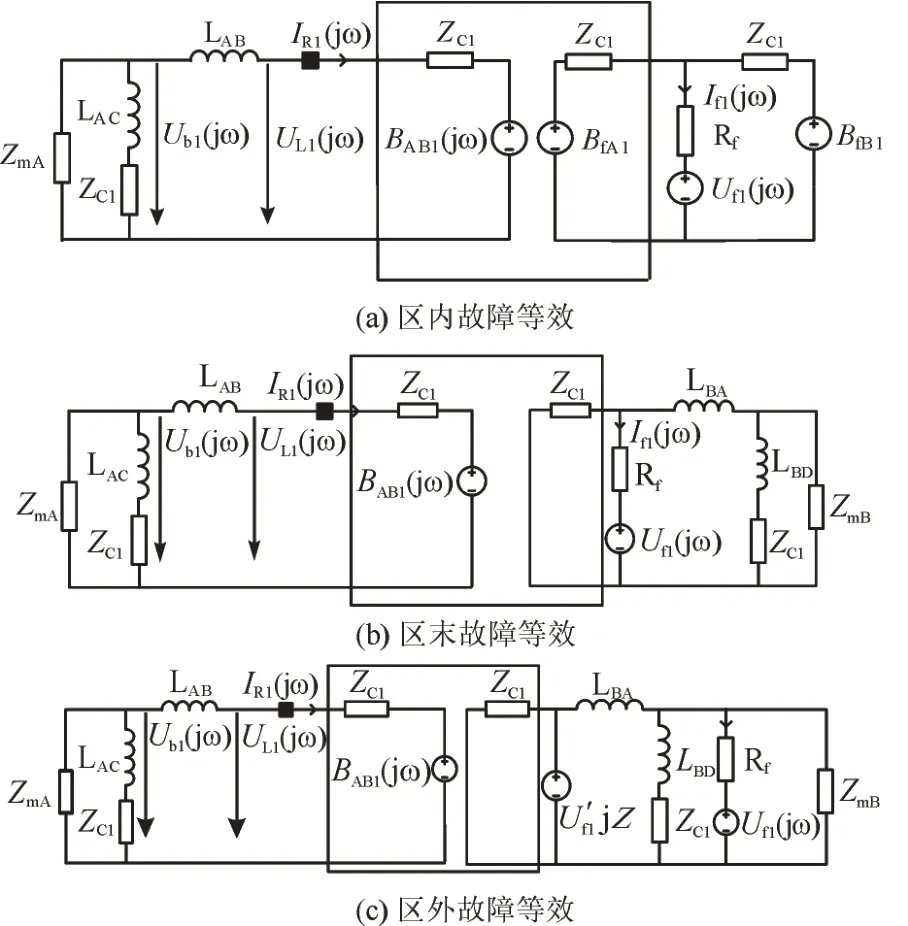
图2 区内外故障等效电路Fig.2 Equivalent circuit for faults inside and outside area
图2 中故障等效线模电压Uf1(jω)为:
式中:Uf(jω) 为故障等效电压的频域表达式;ZC0为零模等效阻抗。
根据贝瑞隆等效电源关系[10]可以得出:
式中:γ(jω)为故障行波的传播常数;l 为故障与线路首端距离。
所以在发生正向故障时,限流电抗器的线路侧与母线侧的电压满足关系式为:
1.2.2 反向区外故障
发生反向区外故障时,故障等效电源作用在换流站A 与限流电抗器之间,等效电路图见图3。
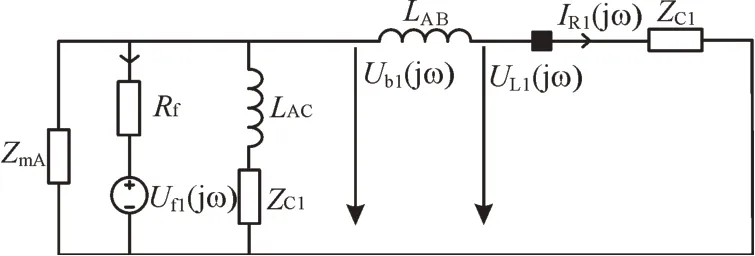
图3 反向区外故障等效电路Fig.3 Equivalent circuit for reverse faults outside area
与文中1.2.1 节分析过程类似,可以得到限流电抗器两侧的电压比为:
1.3 区内外故障差异性分析
故障等效电路以RAB处为研究对象,分别在发生区内外故障情况下对RAB侧限流电抗器两侧电压进行分析并计算出两侧电压比,从式(3)及式(4)中可以得出在发生正向故障与反向故障时差异较为明显,且在高频段时这种差异会更加明显[17]。这种差异性体现在发生正向故障时线路侧高频暂态电压大于母线侧,在发生反向故障时线路高频暂态量小于母线侧,而在发生区内故障、区内末端故障与正向区外故障时LAB两侧电压比值表达式相同。
2 故障电压特定频段暂态能量比特征分析
2.1 区内外特定频段暂态能量比
本研究采取广义S 变换对行波线模信号进行处理[18],提取出频域内的故障信息。采样频率选取为50 kHz,定义电压行波信号某一频段的暂态能量为:
式中:K为S 变换后矩阵某一行元素,即代表信号在某一频段的元素;EK为某一频段暂态能量;uK(t)为变换后时频矩阵内的元素;N为采样点数。
则可以得出频率为K时,限流电抗器的两侧暂态能量比G(无量纲)为:
式中:EKL与EKb分别为限流电抗器线路侧与母线侧的暂态能量;uKL与uKb分别代表频率为K时限流电抗器的线路侧电压与母线侧电压。
本文1.2 节详细推导了发生区内外故障时,换流站A 侧限流电抗器两侧电压比的表达式,并得出了限流电抗器两侧电压表达式以及两侧电压比值。当反向故障发生时,两侧比值小于1;而在发生区内或正向区外故障时,比值表达式相同且均大于1。通过研究区内与正向区外故障的行波传输路径图可得出在发生区外故障时,行波传输路径需要经过更多的限流电抗器[19]。由于限流电抗器具有高频阻滞作用,会对电压行波的高频信号产生削弱作用[20]。并且,当发生区内和正向区外故障时,限流电抗器两侧的频域表达式相同。因此,在发生正向区内故障时[21],特定频段的暂态能量比大于发生正向区外故障时。通过广义S 变换,可以提取出保护RAB侧限流电抗器两侧特定频段的暂态能量,并依据定义的暂态能量比公式,得出特有频段内的G为:
式中:K1,K2为选取的特定频段[22],通过提取出两侧高频暂态能量并计算其比值,依据比值大小准确判断其故障区域。
2.2 暂态能量比频段选取
为了更好地确定保护所需频段,采用广义S 变换提取出0~25 kHz 频段内在发生区内故障与反向区外故障时电压行波数据,并计算出不同频段的暂态能量比值,其中发生区内故障与反向故障时暂态能量比值对比如图4 所示。从图4 中可以看出在大于2.5 kHz的频段时发生区内故障,限流电抗器两侧暂态能量比开始大于发生反向区外故障时,在大于5 kHz 频段2 个暂态能量比曲线关系趋于平稳,区内与正向区外对比如图5 所示,区内故障的暂态能量比也是在大于2.5 kHz的频段时开始大于正向区外故障并在5 kHz 时的趋势逐渐平稳。综合考虑保护方案的抗噪声干扰能力,在保证保护动作准确动作基础上选取较低频段,本文选取频段5~10 kHz 进行区内外故障判别。
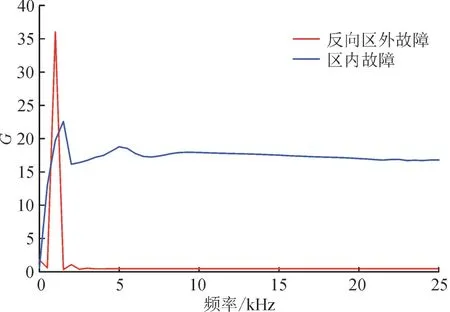
图4 区内故障与反向区外故障暂态能量比值频域对比Fig.4 Frequency domain comparison of transient energy ratio between faults inside area and reverse faults outside area
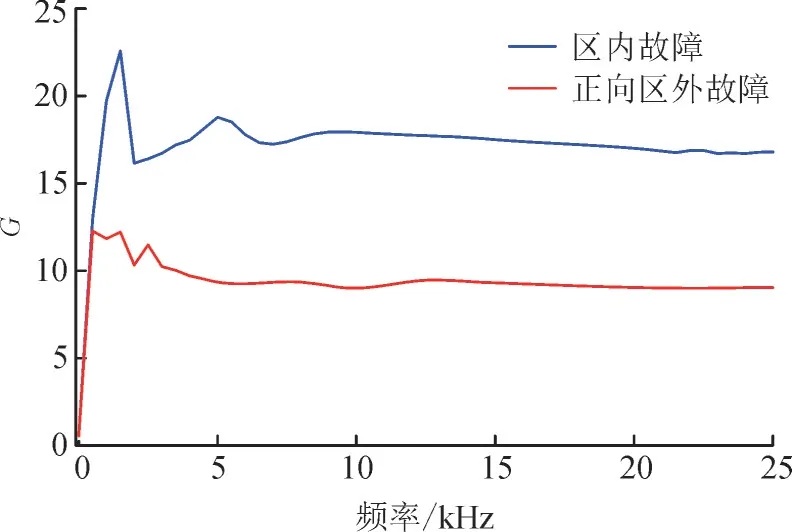
图5 区内故障与正向区外故障暂态能量比值频域对比Fig.5 Frequency domain comparison of transient energy ratio between faults inside area and forward faults outside area
3 基于限流电抗器两侧特定频段暂态能量比的保护方案
3.1 启动判据
启动判据是整个保护方案快速、准确动作的前提,本文采取电压变化率作为启动判据,公式为:
式中:u为故障线路电压;Δuset为整定门槛值,设置为500 kV/ms。
3.2 区内外识别判据
设定暂态能量比阈值分别为Gset1与Gset2,当暂态能量比小于Gset1时,判断出为反向故障;当大于Gset1并且小于Gset2时,判断出为正向区外故障;当大于Gset2时,判断为解数区内故障。将整定值Gset1整定为1,Gset2的整定可按照区内末端发生故障与最不利的正向区外故障测量值进行整定,可靠系数Krel设为1.2。将KrelGset1与KrelGset2分别表示成Kset1与Kset2,判据公式为:
3.3 故障选极判据
由于柔直线路为双极结构,因此发生故障时需要可靠的选极判据,正极与负极线路电抗器的电压表达式为:
式中:VL为限流电抗器电压;L为限流电抗器的电抗值;i 为故障电流值。
在发生单极故障时故障极的电流会在短时间内迅速上升,故障极限流电抗器电压发生显著变化,根据这个特征构造保护判据为:
式中:ΔuL为正极与负极限流电抗器电压幅值差;uL+和uL-分别为正极与负极限流电抗器的电压值。
依据发生不同故障时ΔuL的变化幅度不同,得出保护判据如下:
式中:ΔuLset为整定值。
在发生双极短路时,正负极故障电流变化幅度基本相同,整定值需按照有利于对单极故障进行整定。通过大量仿真分析可以得出,双极短路时ΔuL的最大值不超过5 kV。鉴于可能存在干扰等影响因素,综合考虑选取ΔuLset为8 kV 作为整定值,可靠系数Krel为1.2。
3.4 方案流程
设计的保护方案如图6 所示,通过实时采集电压信号,计算出电压变化率判断是否发生故障。若发生故障,则保护方案启动,选取数据时间窗为故障启动前后各1 ms 数据,计算出限流电抗器线路侧与母线侧该频段暂态能量比判别故障区域。取故障启动后1 ms 时间窗数据,通过判别正负极限流电抗器电压变化幅度差值进行故障选极。
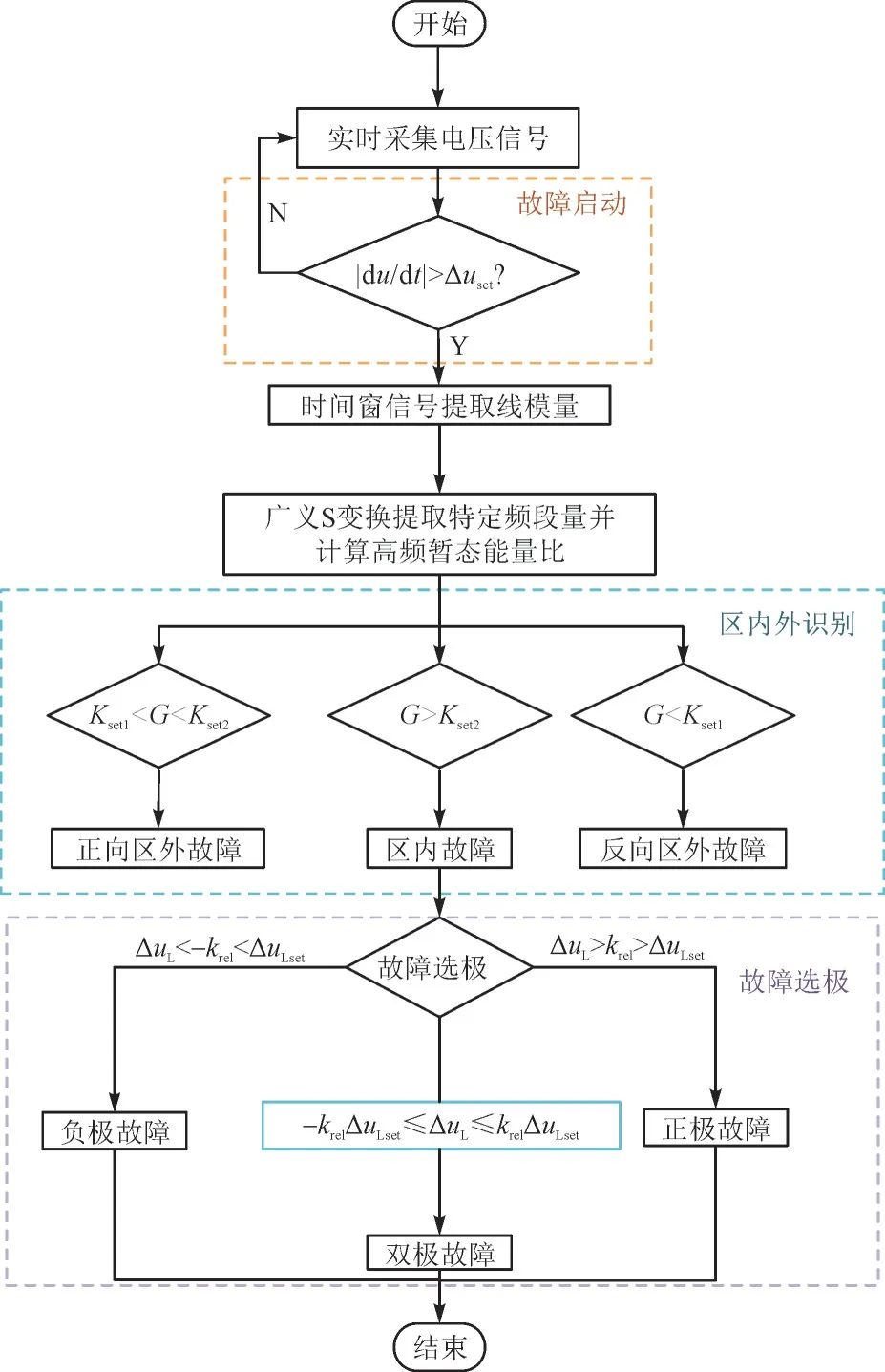
图6 保护流程Fig.6 Protection process
4 仿真分析
4.1 限流电抗器两侧高频暂态能量比整定值选取
本文在PSCAD 仿真平台搭建四端仿真模型,设置的故障位置见表1。
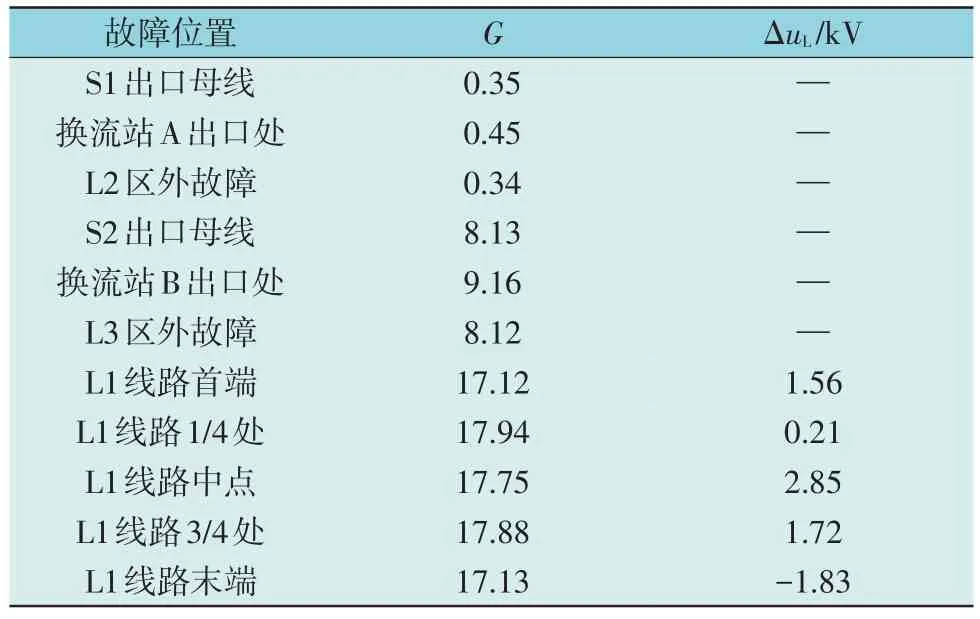
表1 不同故障位置G与ΔuL测量值(双极短路)Table 1 Measurement value at different fault location G and ΔuL(bipolar short-circuit)
发生双极故障时测得G值及ΔuL为如表1 所示。在同样的故障位置上设置单极短路并测量出G值和ΔuL,结果如表2 所示。

表2 不同故障位置G与ΔuL测量值(单极短路)Table 2 Measurement value at different fault location G and ΔuL(single-pole short-circuit)
从表1 和表2 的测量数据中可以得出,发生单极短路和双极短路的暂态能量比差别不是很大。因此,可以按照躲过正向区外故障时的最大值来整定Gset2值,以便准确判别区内故障。在发生正向区外故障时,F6 为正向区外最不利于判别的正向区外故障,此时测得的G值为正向区外故障的最大值。可以得出区外故障时G值最大不超过10,综合考虑将Gset2设定为10 并考虑一定裕度,有利于更精确地判断区内故障。
4.2 区内故障仿真验证
以图1 中L1 线路发生区内故障为例,过渡电阻为0.01 Ω,故障时间设置为1 s,图7 为采集到的故障线路电压变化率。从图7 中可以看到当检测到电压变化率的绝对值大于500 kV/ms 时保护启动,故障发生后0.34 ms 检测到电压变化率大于整定阈值,保护启动并计算特定频暂态能量比,通常固态断路器动作时间为50 μs,则可在故障后1.39 ms 完成保护动作,所以本文所提保护方案在1~2 ms 内完成保护,满足主保护动作要求。
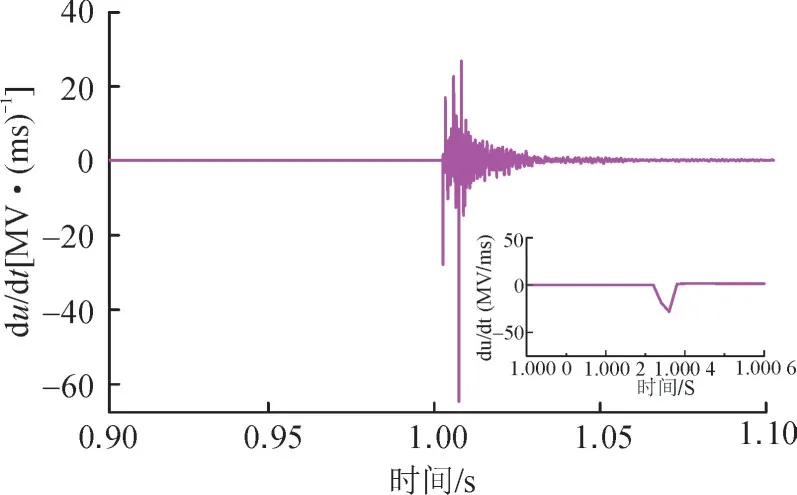
图7 故障电压变化率Fig.7 Change rate of fault voltage
图8 为区内不同故障位置双极短路时ΔuL变化情况,可以看出在不同故障位置发生双极短路ΔuL值均变化不大且接近于零,满足双极短路判定条件,可判定为区内双极短路故障。
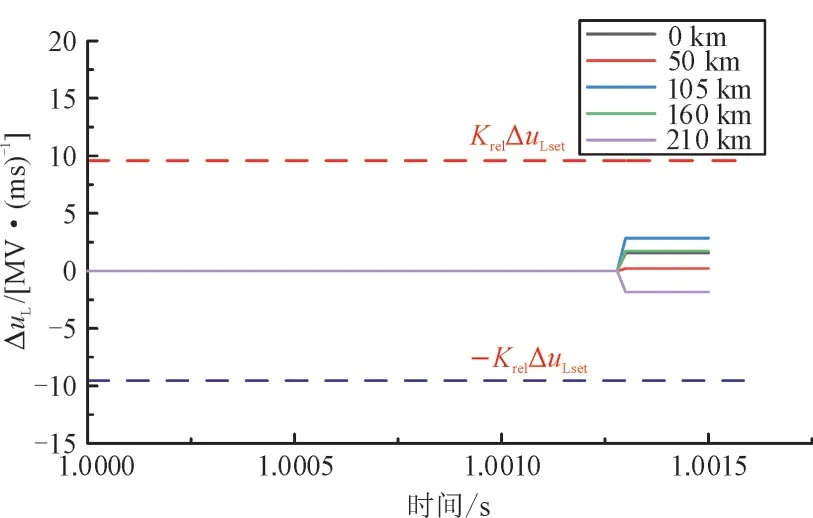
图8 不同故障位置双极短路ΔuL变化Fig.8 Change in ΔuL with different fault location when bipolar short-circuit fault occurs
图9 为区内发生单极接地及双极短路时不同故障位置的暂态能量比,可以看出不同故障位置暂态能量比值均大于Kset2,且G值几乎不受故障类型影响。

图9 区内故障验证Fig.9 Fault verification inside area
4.3 区外故障验证
当发生正向区外和反向区外故障时,以图1 中最不利于保护动作的F6 和F7 故障为例,仿真结果如图10 所示。
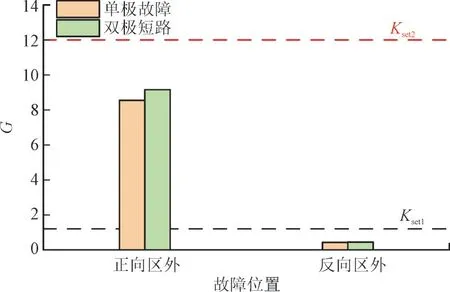
图10 区外故障验证Fig.10 Fault verification outside area
从图10 中可以看出暂态能量比值位于Kset1和Kset2之间,可以判断出为正向区外故障。而发生反向区外故障时,测得故障暂态能量比小于整定值Kset1,判断出为反向区外故障,发生单极接地和双极短路时G值差别不大,且均符合区外故障判据,可正确判断为区外故障。
4.4 不同过渡电阻对保护判据影响
故障位置如图1 所示F1-F7 处,过渡电阻分别设置为0.01 Ω,100 Ω和300 Ω,在不同位置时不同过渡电阻的仿真结果如表3 所示。
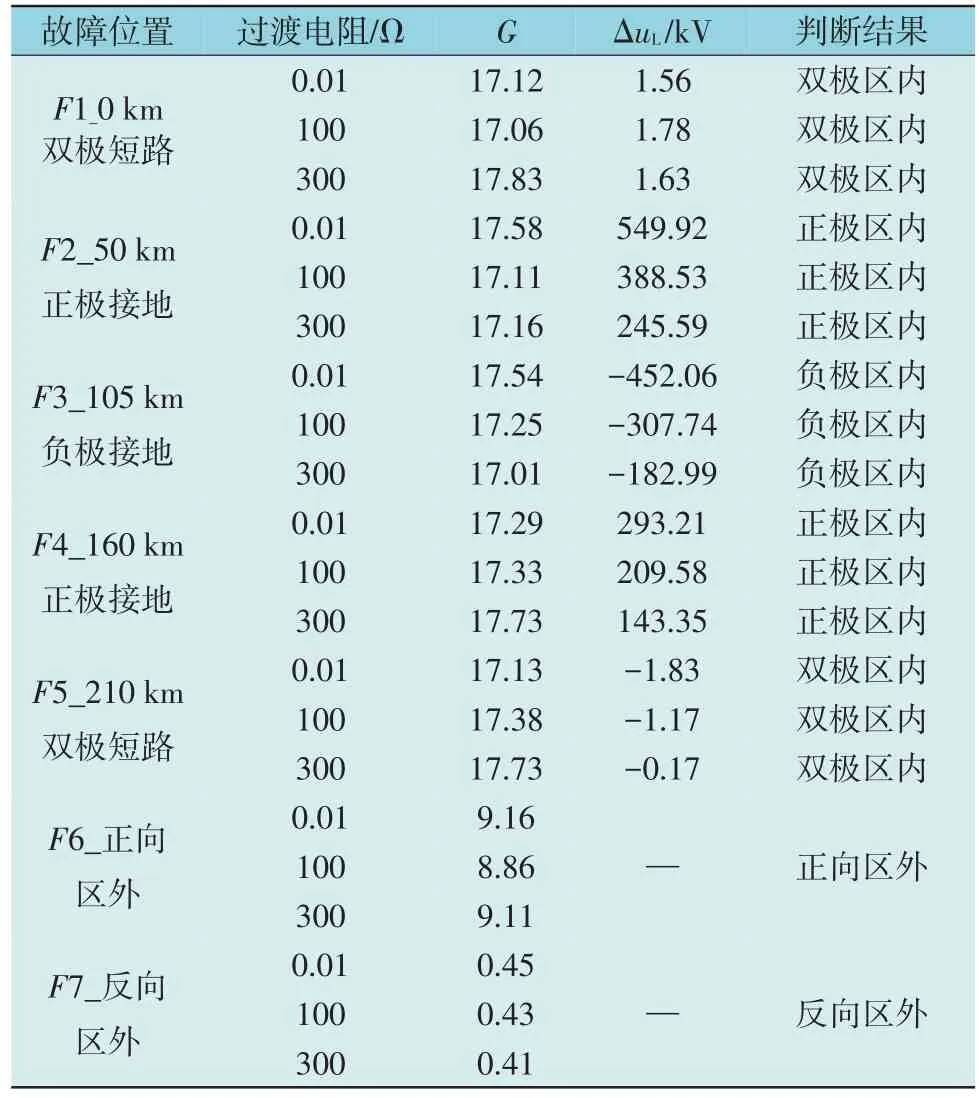
表3 不同过渡电阻时保护判别结果Table 3 Distinguishing results of protection under conditions of different transition resistances
通过式(3)可知过渡电阻不会影响暂态能量比,通过仿真也验证了理论分析结果。从表3 中的G值与ΔuL值变化可知对于不同类型的高阻故障,能够正确识别区域并完成故障选极。
4.5 噪声影响
由于保护的收信与发信以信号的形式传播,较容易受到噪声干扰。由于目前的测量装置所受噪声的干扰信噪比大于等于30 db[23],所以本研究以图1中区内故障F3,正向区外故障F6,反向区外故障F7发故障为例。图11 为F3 双极故障时采集到的电压信号混入30db 噪声时与未混入噪声时的电压频谱图对比,得出混入30 db 噪声时与未混入噪声时的电压频谱图相差不大,故噪声对于暂态能量影响不大。
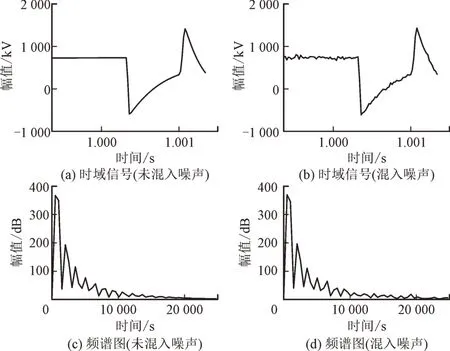
图11 采集电压信号噪声频谱图对比Fig.11 Comparison of noise spectra among collected voltage signals
在向保护RAB侧混入30 db 的噪声后,计算出F3,F6,F7 处发生双极故障时暂态能量比值分别如图12 所示,仿真结果显示暂态能量比会受噪声干扰的微弱影响,但并不影响对结果的判别,本保护方案具有一定的抗噪声干扰能力。
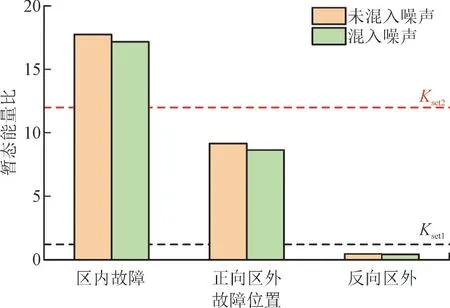
图12 双极短路故障噪声干扰验证Fig.12 Noise interference verification with bipolar short-circuit fault
5 结论
本文基于限流电抗器的高频阻滞作用,构造特定频段电压暂态能量比实现区内外故障识别,利用双极限流电抗器电压幅度差进行故障选极。本文所提保护方法具有如下特点:
1)该保护方案仅需利用单端电压量就能准确区分区内、外故障,在区内末端限流电抗器两侧电压暂态能力比差异性明显,能够准确识别区内末端故障;并且对于区内故障能够准确完成故障选极。
2)所提判据经过理论分析证明不受过渡电阻影响,仿真验证在经不同电阻接地时,过渡电阻几乎不改变暂态能量比值,保护判据具有较强的抗过电阻能力。另外,动作判据抗噪声干扰能力强,可靠性高。
