基于电流误差加权转速自适应律的异步电机无速度传感器设计方法
2024-01-28李琰琰郭磊磊靳雪妍楚之乐
李琰琰,王 帅,郭磊磊,靳雪妍,楚之乐,金 楠
(郑州轻工业大学电气信息工程学院,河南郑州 450002)
0 引言
异步电机因其对恶劣环境适应性强、易维护以及成本低等优点而被广泛应用[1-5]。现有传感器因其精度高、使用便利等优点也被广泛使用[6],然而传感器因工作环境恶劣易被损坏。因此为提高异步电机运行的可靠性,无速度传感器控制策略被广泛研究[7-8]。
目前对于无速度传感器的研究大致分为2 大类,一类基于信号注入法[9-10],旨在通过信号注入使电机低速下实现稳定运行;另一类基于理想模型法[11],通过基于异步电机的基本模型建立观测器的数学模型,包括模型参考自适应算法[12-14]、滑模观测器算法[15-17]、扩展卡尔曼滤波型观测器算法[18-19]以及自适应全阶观测器算法[20-25]等。自适应全阶观测器算法由于其系统更加简单可靠、观测精度更高[20-25],在无速度传感器控制算法中更具优势。然而,在自适应全阶观测器算法中,异步电机在低速范围内运行时稳定性能较差[22],因此需要对其进行改进。文献[22]提出一种双辨识参数的自适应全阶观测器算法,可有效降低低速时定子电阻变化对转速估计精度的影响。文献[23]根据李雅普诺夫稳定性理论,对误差矩阵进行了深入研究,得到了能够实现电机全速范围的稳定运行的反馈矩阵。文献[24]在同步旋转坐标系中设计了一种基于李雅普诺夫方法的速度估计方法,提高了速度观测的精度,但未讨论系统处于低速运行状态的情况。文献[25]将估计的转子磁链误差引入自适应全阶观测器的速度估计算法中,减少了由电机参数偏差引起的估计速度误差,提高了速度估计精度,但未提及如何选择权重系数。
综上所述,本文针对异步电机无速度传感器低速运行不稳定的问题,提出一种基于电流误差加权转速自适应律的设计方法。研究的创新之处在于:采用励磁电流误差对转子磁链误差进行补偿,提高了系统低速带载运行的稳定性。实验分析表明,所提方法能够实现低速带额定负载稳定运行,且比常规方法具有更强的抗负载扰动能力和更快的转速调节能力。
1 异步电机及全阶观测器模型
在两相静止参考坐标系下,选择电机定子电流和转子磁链作为状态变量,异步电机的状态方程为:
式中:isα,isβ分别为α,β轴定子电流;ψrα,ψrβ分别为α,β轴转子磁链;Rs,Rr分别为定子和转子电阻;Ls,Lr,m分别为定子、转子电感和互感;σ为漏感系数;δ为漏感系数与电感间的关系式;λr为转子时间常数;ωr为转子角速度;t为时间;usα,usβ分别为α,β轴定子电压。
根据异步电机的状态方程可推导得到全阶观测器的数学模型为:
根据李雅普诺夫稳定性理论,由观测器误差方程可推导出静止坐标系下的转速自适应律为:
式中:Eisα,Eisβ分别为α,β轴定子电流误差;,分别为α,β轴转子磁链误差;kP,kI为比例积分(Proportional Integral,PI)调节器的比例和积分系数;为积分项。
2 自适应全阶观测器的设计
自适应全阶观测器的设计主要是对自适应全阶观测器中的转速自适应律进行改进。核心设计思路是:首先,基于小信号线性化模型对转速自适应律进行改进;然后,对加权系数进行选择;最后,将改进后的转速自适应律的极点与常规方法的对比,证明所提设计方法具有更好的稳定性。
2.1 基于小信号线性化模型的转速自适应律改进
传统转速自适应律忽略了转子磁链误差项,导致转速观测值误差较大、稳定性较差[26]。为解决该问题,本文提出利用励磁电流误差补偿转子磁链误差来改进转速自适应律的设计方法,以提高电机低速无速度传感器运行稳定性。
当电机稳定运行时,认为ψrd=misd,ψrq=0。其中,ψrq为q轴转子磁链,isd为d轴定子电流,为q轴转子磁链的观测值。因此将式(5)中的转子磁链误差项变换到旋转坐标系dq上,可得转子磁链误差为:
由于模型参数不匹配等因素的影响,转子磁链的观测值会产生一个较小的转子磁链角度误差,此时,对电机稳态时参数在旋转坐标系中的分量进行线性化处理,可得定子电流与转子磁链在实际和估计的d,q轴的分布如图1 所示。
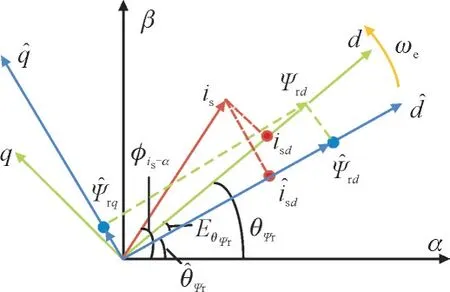
图1 定子电流和转子磁链在实际和估计的d,q轴的分布Fig.1 Distribution of stator current and rotor flux on actual and estimated dq axis
图1 中,,轴为旋转坐标系dq的估计值,is为定子电流,ϕis-α为is与α轴之间的夹角,θψr为转子磁链角度,为转子磁链角度的观测值,为d轴定子电流的观测值,ψrd为d轴上的转子磁链,为d轴上的转子磁链观测值,ωe为同步角速度。
由图1 可得以下关系为:
式中:ϕis-d为is与d轴间的夹角;为is与轴间的夹角;isq为q轴定子电流;为q轴定子电流的观测值。
将式(7)代入式(6)中可得转子磁链误差为:
由式(8)可知,与成正比。然而,由于θ的实际值未知,因此也很难直接得到。
考虑到异步电机的ψr与isd直接相关,且常规的转速自适应律忽略后仅与isq有关[22]。本文尝试分析与d轴定子电流误差之间的关系,在传统的转速自适应律中增加,从而补偿提高电机低速运行稳定性。
由于稳态时很小,可令cos≈1。因此,由式(7)可得最简化的d轴电流误差表达式为:
将式(9)代入式(8)中,对式(6)进行化简,然后代入式(5)并变换到同步旋转坐标系上。此外,考虑到稳态时为1 个常数量,所以可将其乘入PI增益中,最终可得本文所提的改进转速自适应律模型为:
式中:kP1,kI1为本文所提的PI 调节器的比例和积分系数,调整kP1,kI1的值即可实现转速的估计;N为加权系数。
由式(10)可知,本文提出的改进转速自适应律包含q轴定子电流误差和。当和收敛于0 时,即可得到。该方法由于未忽略Eψr,而是采用对进行补偿,从而有助于提高无速度传感器控制精度。本文中kP1,kI1通过试凑法得到[27-29],N通过使用MATLAB 软件进行稳定性分析来确定,具体理论分析过程如2.2 节所示。因此,实际在设计参数kP1,kI1,N时,并未使用。
2.2 加权系数N的选择
由式(10)可知,N与电流、磁链等多个变量有关。当N=0 时,即可得到常规的转速自适应律;当N≠0 时,可通过合理选择N的取值,提高异步电机无速度传感器控制精度。对全阶观测器进行推导,可得转子角速度误差到d轴电流误差的开环传递函数Gd,Eωr到q轴电流误差的开环传递函数Gq,其表达式分别为:
式中:p为微分项;ωf为转差角速度;F,H分别为ωe和p的系数。
根据式(10)—式(14)可得改进的速度观测算法框图如图2 所示。
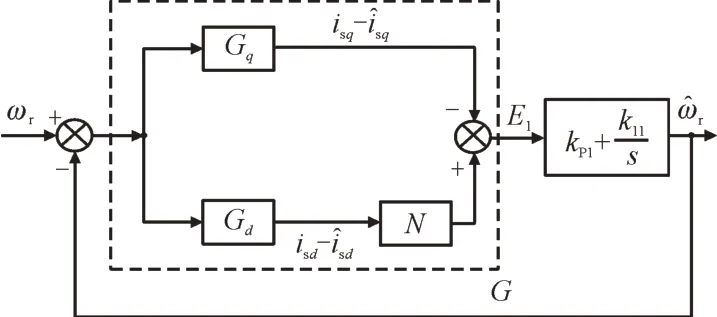
图2 改进的速度观测算法框图Fig.2 Block diagram of improved speed observation algorithm
根据式(10)以及图2 可得Eωr到改进的转速自适应误差E1的开环传递函数G为:
式中:z为ωe与p和的关系式。
由于文献[23]中的反馈矩阵不仅实现了电机全速范围的稳定运行,而且实现了低速稳定运行。因此,本文使用该反馈矩阵,其表达式为:
式中:l为可调参数。
将式(12)、式(13)及式(16)代入式(15)中,可得具体的开环传递函数表达式为:
式中:b3,b2,b1分别为p3,p2,p的系数;a0为常数项。
根据劳斯稳定性判据,对式(17)所示的开环传递函数进行分析,可得满足全速范围系统稳定运行的条件为:
由于根据式(17)不易直接计算出N的取值范围,因此本文使用MATLAB 软件,根据式(17)和式(19)画出N与ωe稳定性的关系,如图3 所示。其中,N位于蓝色区域时会导致系统失稳,而N位于白色区域时系统能够稳定运行。
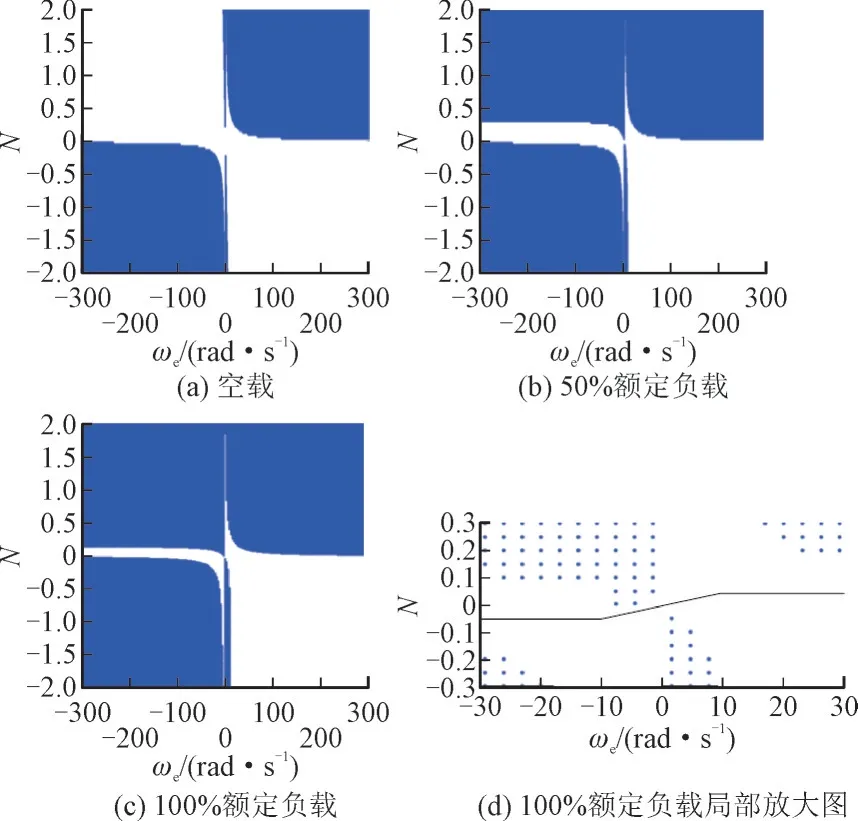
图3 N与ωe 稳定性的关系Fig.3 Relationship between N and stability of ωe
由图3 可知,随着负载的增大,白色区域逐渐减小,表明N的取值范围逐渐减小。由图3(d)可知,ωe为0 Hz 时稳定区域很窄,而其他频率下稳定区域较宽,说明电机在低速运行时,负载越大越不稳定,与实际情况相符合。
当定子频率为0 时,N需要穿过1 个较窄的缝隙。定子频率为0 时的加权系数N0可根据a0=0 计算得出,其表达式为:
结合图3 可知,在100%额定负载下确定的N值亦可满足其他负载下电机的运行稳定。因此确定N的取值为3 种情况:当ωe≥10 时,N=0.035;当ωe≤-10 时,N=-0.05;当-10<ωe<10 时,N=0.004 25ωe+N0。0.004 25 为穿过100%额定负载0 Hz 时的斜率。
2.3 极点分布对比分析
在低速(ωe为0~10π rad/s)额定负载(χ=14 Nm)条件下可得2 种观测器开环传递函数的极点分布,如图4 所示。其中,在含有本文所提改进转速自适应律的系统中加入式(16)所示的反馈矩阵后的改进观测器极点分布情况如图4(a)所示。传统观测器所对应的系统极点分布如图4(b)所示。图中的极点分布是由开环传递函数的分母为0 得到,实轴表示开环传递函数的分母中复数的实部,虚轴表示复数的虚部,所以虚轴和实轴并无单位。
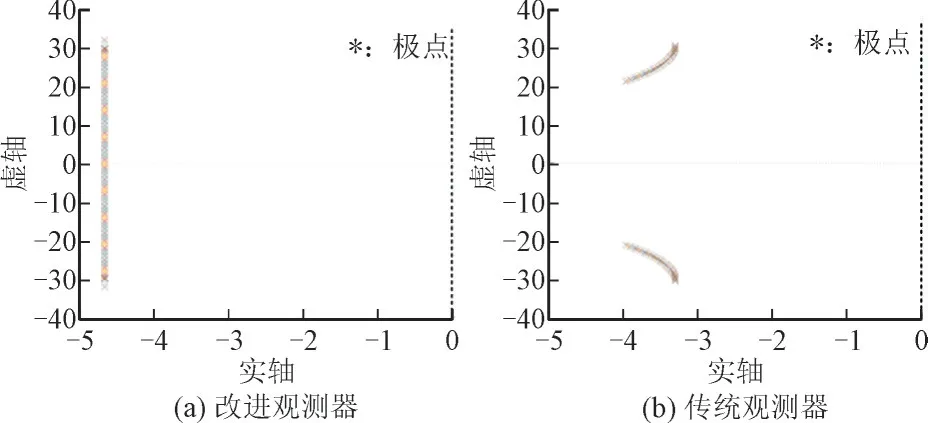
图4 两种观测器开环传递函数的极点分布Fig.4 Poles distribution of open-loop transfer function for two observers
由图4(a)可知,极点全部位于虚轴的左半平面,说明本文所提方法满足系统在低速范围内运行的稳定性条件。由图4(b)可知,与图4(a)相比图4(b)的极点更接近0 轴,这将导致系统稳定性能变差。
3 实验分析
3.1 实验平台及参数设置
为验证本文所提方法的有效性,建立了基于YXSPACE-SP2000 的2.2 kW 异步电机实验平台,并对所提方法进行实验研究。本文采用的异步电机无速度传感器矢量控制系统框图如图5 所示。其中,为转子角速度的参考值,,分别为d,q轴定子电流参考值,usd,usq分别为d,q轴定子电压,iA,iB,iC分别为A,B,C 相电流。
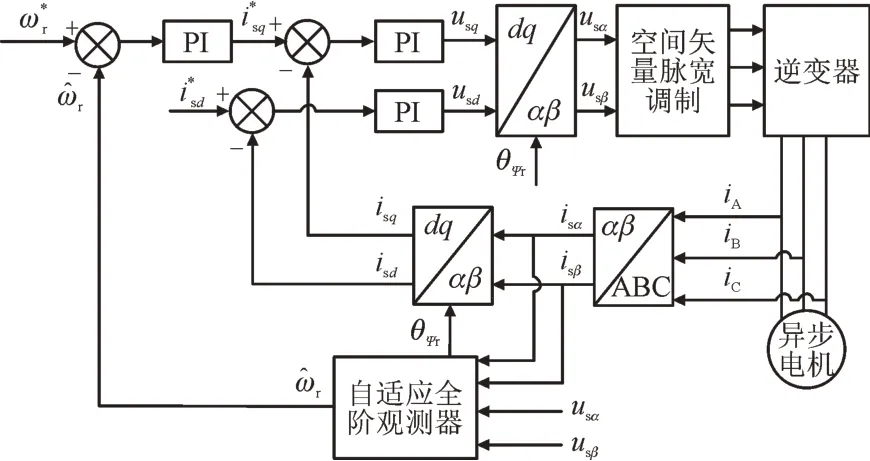
图5 异步电机无速度传感器矢量控制系统框图Fig.5 Block diagram of speed sensorless vector control system for induction motor
由于图5 中的θψr可由得到,因此ωf的表达式可转化为:
异步电机参数如表1 所示。

表1 异步电机参数Table 1 Parameters of induction motor
本文所搭建实验平台如图6 所示。

图6 实验平台Fig.6 Experimental platform
3.2 动态运行实验
根据本文所提方法进行的动态运行实验如图7 所示。其中,设电机参考转速为100 r/min,60 r/min,20 r/min 时的空载减速实验波形如图7(a)所示。设电机参考转速为30 r/min,50 r/min,70 r/min 时的满载(额定负载χ=14 Nm)加速实验波形如图7(b)所示。其中,nref为参考转速,为转速观测值,n为实际转速。
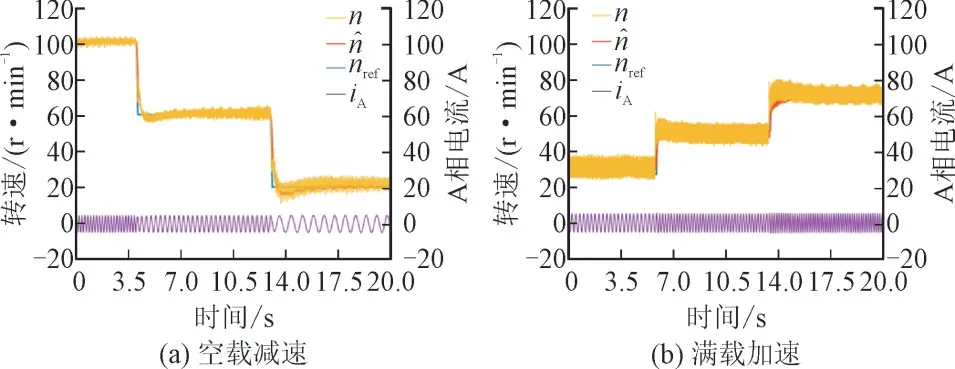
图7 动态运行实验Fig.7 Dynamic operation experiment
3.3 负载突变实验
设电机参考转速为60 r/min、负载转矩由额定负载χ=14 Nm 突减为0 时的突减额定负载实验如图8 所示。
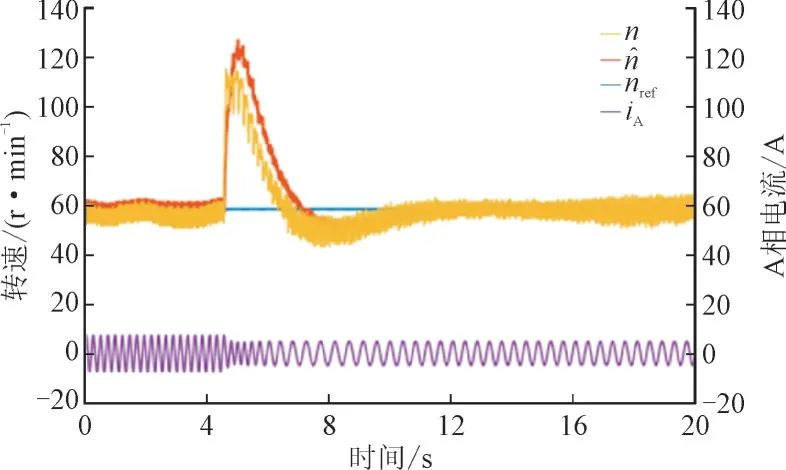
图8 突减额定负载实验Fig.8 Experiment of sudden reduction in rated load
由图8 可知,电机在突减负载过程中可以稳定运行,动态过程中误差仍然较小。这表明本文所提方法具有较强的抗负载扰动能力。
3.4 对比实验
为了进一步证明本文所提方法的优越性,对比研究了所提方法与传统的方法的抗扰性能和转速动态响应性能。
3.4.1 抗扰性能对比
设电机参考转速为50 r/min,突加额定负载时传统方法和本文所提方法的抗扰性能对比如图9所示。
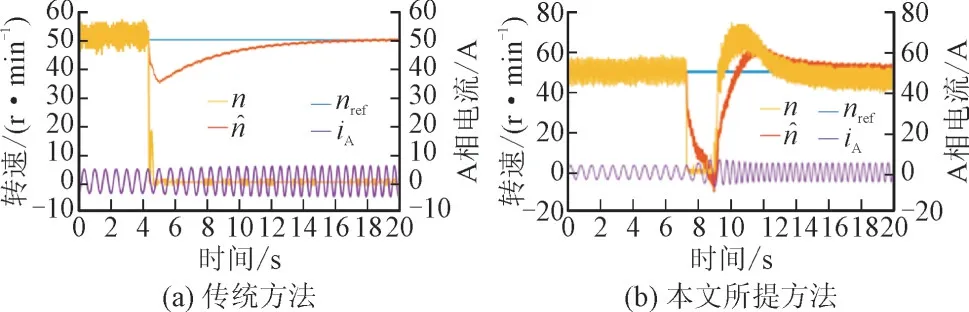
图9 抗扰性能对比Fig.9 Comparison of anti-interference performance
由图9(a)可知,在低速突加额定负载时,传统方法下电机的n为0,无法实现转速跟踪和无静差控制。由图9(b)可知,本文所提方法在低速突加额定负载时仍能实现稳定运行。说明本文所提方法在电机低速突加负载运行时具有更强的抗负载扰动能力。
3.4.2 转速动态响应性能对比
设电机参考转速为50 r/min,空载时传统方法和本文所提方法的转速动态响应性能对比如图10 所示。
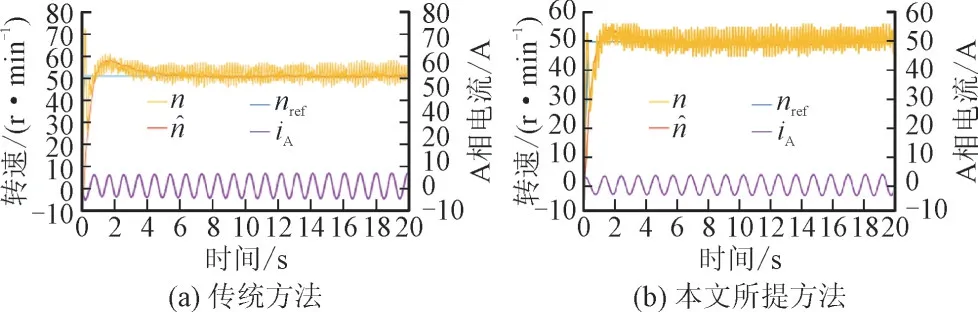
图10 转速动态响应性能对比Fig.10 Comparison of speed dynamic response performance
由图10(a)可知,当采用传统方法时,异步电机在0.2 s 时产生了1 个70 r/min 的尖峰,且在1.5 s时出现9 r/min 的转速超调。由图10(b)可知,采用本文所提方法时,异步电机产生的转速尖峰明显减小,转速超调也减小为4 r/min。说明本文所提方法具有更好的动态转速控制性能。
4 结语
针对异步电机无速度传感器低速运行不稳定的问题,提出一种基于电流误差加权转速自适应律的设计方法。在传统转速自适应律的基础上引入d轴电流误差项,补偿常被忽略的转子磁链误差项,提高了电机的低速带载无速度传感器控制的运行稳定性。从理论上详细介绍了所提方法的原理,给出了加权系数的设计原则,并与常规方法进行对比,分析了系统的稳定性,证明了所提方法的有效性。最后,通过不同工况下的对比实验研究验证了所提方法的可行性和优越性。
