考虑需求侧响应的配电网无功补偿装置协调优化
2024-01-28任彦辉宋景龙王文清武建铭
任彦辉,宋景龙,余 瑞,王文清,邢 波,武建铭
(1.国网酒泉供电公司,甘肃酒泉 735099;2.兰州交通大学自动化与电气工程学院,甘肃兰州 730070)
0 引言
在“双碳”目标和全球能源革命的背景下,新能源产业迎来了高质量、跨越式的发展[1]。大量以光伏(Photovoltaic,PV)为代表的大规模新能源接入使得配电网结构变得更加复杂,新能源出力的不确定性给配电网的无功平衡和电压稳定等方面带来了新的问题[2]。在配电网适当位置安装电容器组(Capacitor Bank,CB)或静止无功补偿器(Static Var Compensator,SVC)等无功补偿设备,对其进行控制和调度可改善电压分布和减少功率损失[3]。但仅仅按规定方式对配电网进行静态固定容量无功补偿配置,则可能无法使得配电网的安全性、稳定性和经济性同时达到最优。因此,针对配电网无功补偿装置协调优化问题的相关研究很有必要。
配电网无功优化属于多目标多约束条件的非线性优化问题[4]。目前针对配电网无功优化问题基本采用算法求解,线性规划法、非线性规划法和混合整数规划法等传统算法的理论完善,复杂度小,但在处理离散变量和全局最优方面存在一定的不足[5]。随着人工智能算法的快速发展,以遗传算法(Genetic Algorithm,GA)、粒子群(Particle Swarm Optimization,PSO)等为代表的启发式搜索算法为解决配电网无功优化问题提供了新的思路[6]。文献[7]提出一种以电力系统有功网损最小为目标函数的配电网无功优化模型,通过选用改进的蜉蝣算法(Mayfly Algorithm,MA)对配电网无功优化模型进行求解。文献[8]以含新能源的地区配电网为研究对象,提出一种基于Attention-LSTM 算法的配电网在线无功优化方法。文献[9]以配电网经济运行和系统电压质量最优为目标函数,建立动态网络重构与无功电压调整协同优化双层模型,并采用改进鲸鱼优化算法(Whale Optimization Algorithm,WOA)和内点法相结合的混合策略对模型进行求解。虽然文献[8-9]能够实现无功补偿装置位置与容量的优化配置,但其设计的目标函数较为单一,对关键节点的优选考虑不足,优化求解方法容易陷入局部最优。
随着电力市场改革,将需求侧响应(Demand Response,DR)引入到电力系统的调控范围内,对减少电网的运行成本、降低电网供电压力及维持电网稳定运行具有重要意义[10]。文献[11]提出一种基于DR 的优化调度模型来提高综合能源系统对新能源的消纳能力。文献[12]以DR 作为出发点,提出一种基于DR 的新能源消纳优化模型,并通过直接非劣解法对模型进行求解。但是引入DR 后,针对含PV的配电网如何充分发挥各无功补偿设备和DR 技术的协同优化问题具有重要研究价值。
基于此,本文在已有研究的基础上建立基于DR 的配电网无功补偿优化双层模型;针对模型特征,上层模型采用猎人猎物优化算法(Hunter-Prey Optimizer,HPO)进行求解,下层模型通过采用改进的快速非支配排序的遗传算法(Non-dominated Sorting Genetic Algorithm-Ⅱ,NSGA-Ⅱ)进行求解;最后在IEEE-33 节点系统中的算例验证了所提方法的有效性和性能优势。
1 无功补偿装置优化配置双层模型
1.1 双层优化模型
双层优化问题是一种具有双层递进结构的系统优化问题,上下层模型相互影响,相互制约[13]。双层优化模型为:
式中:F和f分别为上、下层模型的目标函数;G,g和H,h分别为上、下层模型不等式约束条件和等式约束条件;w为上层模型的目标值;xup和xl0分别为上、下层模型的决策变量。
本文所建立的基于DR 的配电网无功补偿装置优化模型如图1 所示。
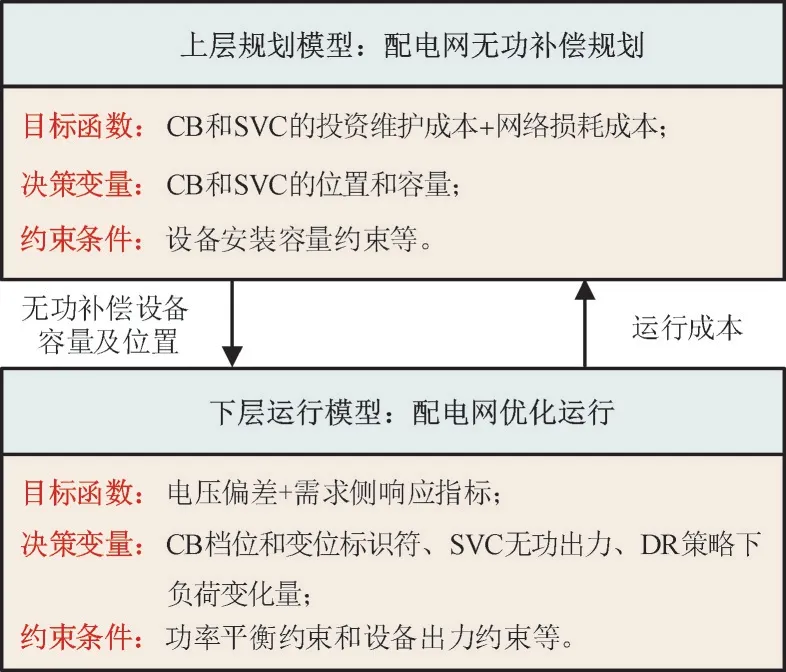
图1 配电网无功补偿双层优化模型Fig.1 Bi-level optimization model for reactive power compensation in distribute network
1.2 上层规划模型
上层模型以配电网经济运行为目标,考虑CB和SVC 投资运行成本和配电网的有功网损,但配电网有功网损属于系统运行的技术指标,将其转化为经济指标有功网损成本,建立无功优化上层模型,且各项经济指标均已转折算到以年为单位[14]。
1.2.1 上层模型目标函数
配电网网络年损耗成本fploss如式(4)所示:
式中:Pn,t和Qn,t为n节点t时刻有功功率和无功功率;Vn,t为n节点t时刻电压;κ为网损电价;Rn为第n条支路的电阻。
上层模型目标函数Fup为:
1.2.2 上层模型约束条件
1)CB 容量约束
2)SVC 容量约束
3)总无功补偿装置容量小于无功负荷的75%,即:
式中:Qc,h为第h台无功补偿装置的容量;Qn,load分别为节点n负荷的无功功率;K为无功补偿装置总安装组数。
1.3 下层运行模型
以配电网运行过程中以及电压偏移度最小为目标,结合在价格激励下负荷的灵活性,建立考虑DR 的配电网无功优化下层运行模型。
1.3.1 基于电价的DR
DR 主要包括基于电价的DR 和基于激励的DR2 种模式。本文主要考虑基于电价的DR,该模式下,用户的可转移负荷部分可根据电价信号进行调整,其约束条件为:
满足式(9)约束的情况下引入用户舒适度和经济性函数来表征考虑DR 后用户的舒适性和经济性,舒适度fcom函数[1]如式(10)所示,其值越大,表明用户舒适度越高。
经济性函数feco的表达式如式(11)所示,其值越大,表明用户考虑DR 后用电成本变化越大,经济性越好。
1.3.2 下层模型目标函数
电压偏移度fvol为:
定义下层模型的目标函数Flo如式(13)所示。
式中:η1和η2分别为目标函数的权重,且η1+η2=1,η1和η2的计算可通过层次分析法求得[15]。
1.3.3 下层模型约束条件
1)DR 约束满足式(9)[16]。
2)功率约束:系统有功和无功功率需要满足式(14)的约束。
式中:Ps和Qs分别为系统有功和无功功率;Pm,lineloss和Qm,lineloss分别为支路m的有功和无功损耗;Pn,load为节点n负荷的有功功率;Mb为支路总数。
3)不等式约束
下层模型的不等式约束主要有PV 出力约束、无功补偿容量约束、CB 投切次数约束和节点电压约束。
PV 出力约束满足式(15):
节点电压约束满足式(16):
式中:Vn,t,min和Vn,t,max分别为n节点t时刻电压的最小值和最大值。
节点安装的无功补偿装置容量满足式(17)。
式中:Qcmin和Qcmax分别为无功补偿装置容量的最小值和最大值。
CB 投切次数也有一定的限制,其投切次数需满足如式(18)所示的约束条件:
2 无功补偿装置优化配置模型求解算法
2.1 基于HPO优化算法的上层模型求解
HPO 优化算法是一种基于群体的启发式全局智能搜索优化算法[17]。
种群初始化:根据式(19)初始化种群x={x1,x2,...,xn},可得:
式中:xi为猎人或猎物的位置;u和l为问题变量的上下限;d为问题变量的数量。
设置算法相关参数:HPO 算法的猎人的搜索机制如式(20)所示:
式中:xi(t)和xi(t+1)分别为第i个猎人或者猎物当前的位置和下一次迭代的位置;Ppos(j)为猎物的第j维的位置;C为平衡参数,其计算如式(21)所示;Z为自适应参数,其计算如式(22)所示;μ为所有搜索位置的均值,计算如式(23)。
式中:it和it,max分别为当前迭代次数和最大迭代次数。
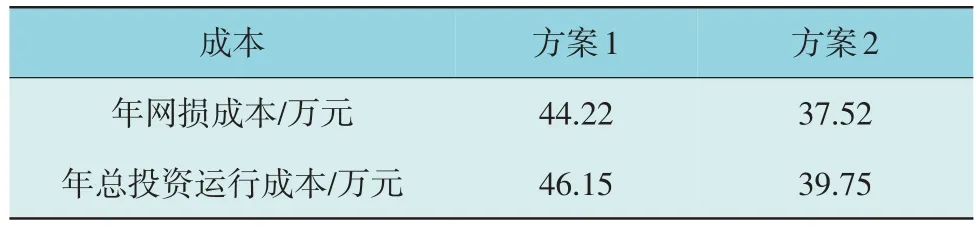
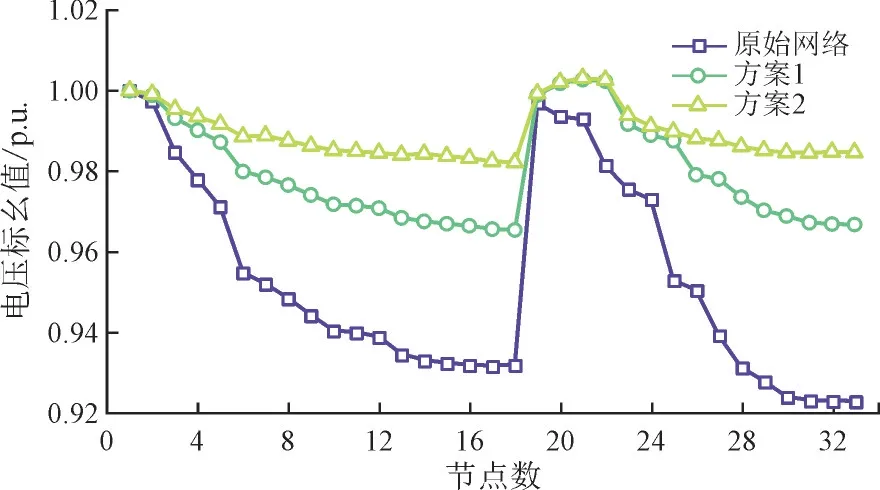
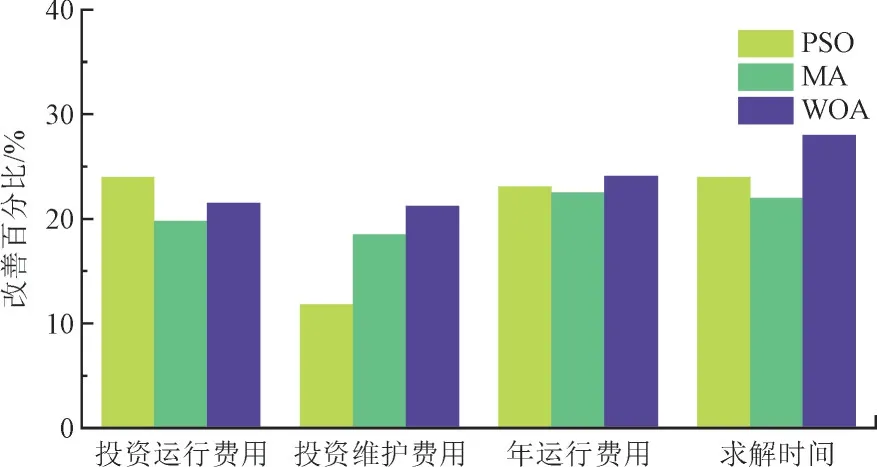
式中:R1和R3为随机向量,且R1,R3∈[0,1];R2为随机数;P为R3 式中:n为猎物种群数。 HPO 算法的猎物的搜索机制为: 式中:Tpos为全局最优位置;β为调节参数,本文取值为0.1;R4为[-1,1]范围内的随机数。 由于HPO 算法能够模拟猎人和猎物的竞争与逃避策略,可以全局搜索函数最优解,并通过观察猎物的运动状态,猎人可以快速地调整自己的位置,具有较高的收敛速度。与PSO 算法以及其他智能算法相比,HPO 算法具有更好的寻优性能。本文建立的双层规划模型要求收敛精度高,收敛速度快,上层模型选用HPO 算法可以更有效地收敛到全局最优解。 NSGA-Ⅱ算法采用了快速非支配排序算法,降低了计算的复杂度,在解决一些极凸或极凹问题时可以保留较多的边界解。具体的NSGA-Ⅱ算法步骤见文献[18]。由于下层模型的目标函数维数为2,因此采用NSGA-II 算法能够同时做到对收敛性和多样性的保证。基于NSGA-Ⅱ算法对下层模型进行求解,得到符合条件的帕累托最优前沿解集,需要从这个解集中找到一个最优折衷解并返回到上层模型中。 本文采用模糊隶属度函数[19]来分别表示每个帕累托解集中各个目标函数对应的满意度,模糊隶属度函数如式(25)所示,当Hi=1 时表示对某个目标函数值完全满意。 式中:ui为第i个目标函数值;uimax和uimin分别为目标函数的上、下限。 通过式(26)求解其标准化满意度值,其中满意度值最大的解即为最优折衷解。 式中:h为待优化目标函数的数目。 通过采用HPO+NGSA-II 优化算法对基于DR的配电网无功优化模型进行求解,得到符合约束条件的配电网运行方案。具体流程如图2 所示。 图2 配电网无功优化模型求解流程Fig.2 Solving procedure for reactive power optimization model of distribute network 本文基于IEEE33 节点系统进行算例分析,系统负荷SL=3 715+j2 300 kVA。CB 单组容量为20 kvar,无功补偿单价50 元/kvar,单点无功安装成本为1 万元,LT=10,折现率r=8%。SVC 安装容量上限为1 000 kvar,系统其它参数的取值见文献[1],系统拓扑如图3 所示。 图3 IEEE 33 节点系统拓扑Fig.3 Topology of IEEE 33-bus system 在系统的17 节点和21 节点处安装光伏电源,容量分别设置为250 kW 和750 kW,针对光伏电源和负荷的出力采用季节典型场景,4 个季节典型日光伏电源和负荷出力分别如图4 和图5 所示,DR分时定价参数设置如图6 所示[20]。 图4 光伏典型日出力曲线Fig.4 Curves for typical daily photovoltaic output 图5 典型日负荷曲线Fig.5 Curves for typical daily load 图6 分时电价Fig.6 Time-of-use price 下层目标函数中权重值η1和η2通过利用层次分析法计算得到分别为0.542 和0.458。通过采用灵敏度分析法[21-22]求解得到配电网无功补偿装置候选节点为[32,30,3,2,8,9,14]。 上层HPO 算法参数:种群规模为100,迭代次数为200;下层NSGA-II 算法参数:种群规模为100,迭代次数为100。 3.2.1 不同模型计算结果分析 为了分析本文所提模型与配电网单层模型(固定配置模型)对配电网无功补偿设备投资运行成本、有功网损成本和电压偏移度的影响,分别采用本文选用的HPO 算法对2 种不同配置模型进行计算,所得结果如表1 所示。 表1 不同配置模型计算结果Table 1 Calculation results of different configuration models 由表1 可知,本文模型无功补偿设备配置容量低于确定性模型,因此,本文模型在有功网损和总投资成本方面均低于固定配置模型,这表明本文所建模型具有良好的经济性。 3.2.2 不同策略对比分析 为了对比分析提出的用户侧DR 对配电网经济运行的影响,方案设置如:1)未考虑DR 的无功优化方法;2)考虑DR 的无功优化方法。 采用HPO+NGSA-II 算法进行求解,分别给出2种方案下,配电网无功补偿配置结果以及年均网损成本和年投资成本。2 种方案下的配电网无功优化结果如表2 所示。 表2 不同策略下的无功配置结果Table 2 Reactive power configuration results under different strategies 由表3 可知,相较于方案1,方案2 在年网损成本和年投资运行成本分别减少了15.15%和13.88%。由此可以得出,在考虑DR 后能够有效降低配电网的网损成本,促进配电网经济稳定运行。这是因为引入DR 后,在电价高峰时段,将可转移负荷转移到电价非高峰时段,导致系统日负荷有功和无功功率发生了变化。相较于电价高峰时段,非高峰时段的配电网网损成本下降,从而提高了配电网运行的经济性。 表3 不同策略下的优化结果Table 3 Objective results under different strategies 选取夏季典型日负荷和光伏出力数据进行计算,求得IEEE 33 节点系统在无功优化前后节点电压的分布如图7 所示。 图7 典型场景下无功优化前后节点电压Fig.7 Node voltage before and after reactive power optimization in typical scenarios 如图7 所示,系统原始网络部分节点的电压低于0.95;在经过无功优化后,方案1 和方案2 各个节点电压均能够维持在0.96 以上。相较于方案1,方案2 的各节点电压分布更加均衡,保持在0.98 以上。因此,考虑DR 的配电网无功优化方法不仅能够使得配电网经济运行,而且能够改善配电网节点电压。 3.2.3 不同算法对比分析 为了分析不同算法对本文所建模型求解精度和速度的影响,分别采取PSO,MA 和WOA 算法与本文优化算法进行对比。以本文算法为基准,不同算法对模型指标的改善如图8 所示。 图8 HPO 算法较其他算法各指标改善的百分比Fig.8 Percentage of improvement in indicators of HPO algorithm over other algorithms 如图8 所示,全为正数表明了本文所用算法对各个指标进行了改善。与PSO,MA,WOA 算法相比,本文所采用算法在求解精度和求解速度上具有明显优势,这是因为HPO 算法能够进行全局搜索解空间,不易陷入局部最优解,并且能够快速收敛,在单峰函数寻优方面具有较好的优势。 本文建立考虑DR 的配电网无功补偿装置优化配置双层模型,通过HPO 算法和NGSA-II 算法对双层模型进行求解,实现无功补偿装置优化配置。算例结果验证了模型的有效性和合理性。结果表明: 1)相较于单层无功优化配置方案,双层优化配置模型能够有效降低配电网网损,改善电压质量,提高配电网电压的平稳性和鲁棒性,同时兼顾配电网的经济效益。 2)建立的考虑DR 的配电网无功双层优化模型,能够有效考虑电力市场下用户可转移负荷的影响,引导用户改变用电习惯,从而有效地平抑负荷波动、减小调峰难度、改善配电网节点电压、提高配电网无功优化的经济性。 3)与PSO,MA,WOA 等算法相比,本文混合优化算法中上层采用HPO 算法求解设备优化配置问题,下层采用NSGA-II 算法保证求解精度,具有一定的优势。2.2 基于NSGA-Ⅱ算法的下层模型求解
2.3 配电网无功优化双层模型求解流程
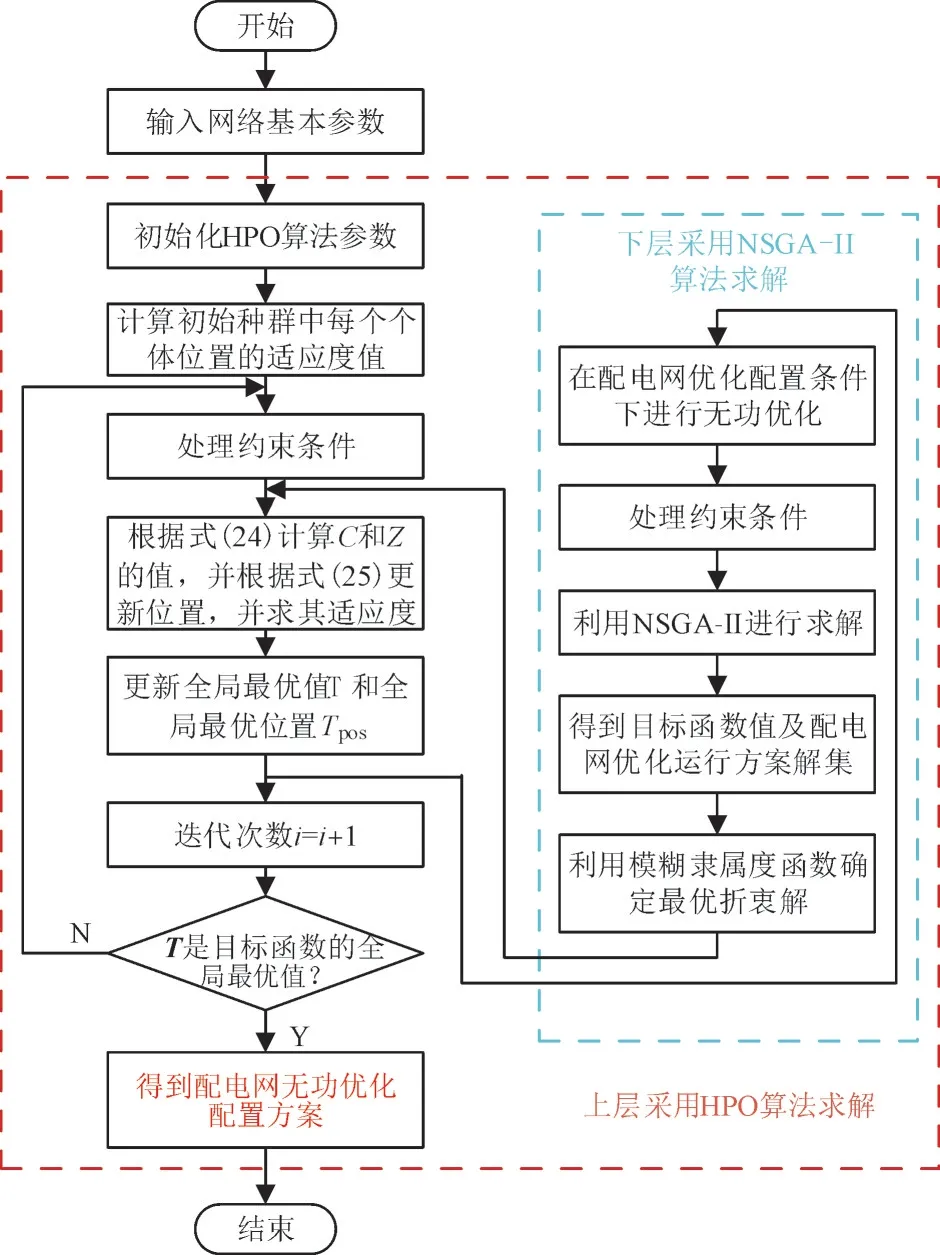
3 算例分析
3.1 算例数据
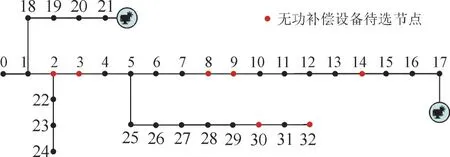
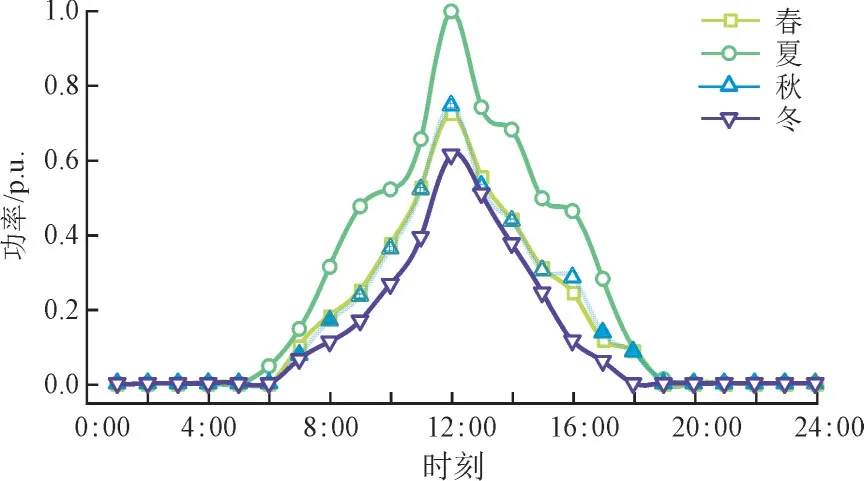
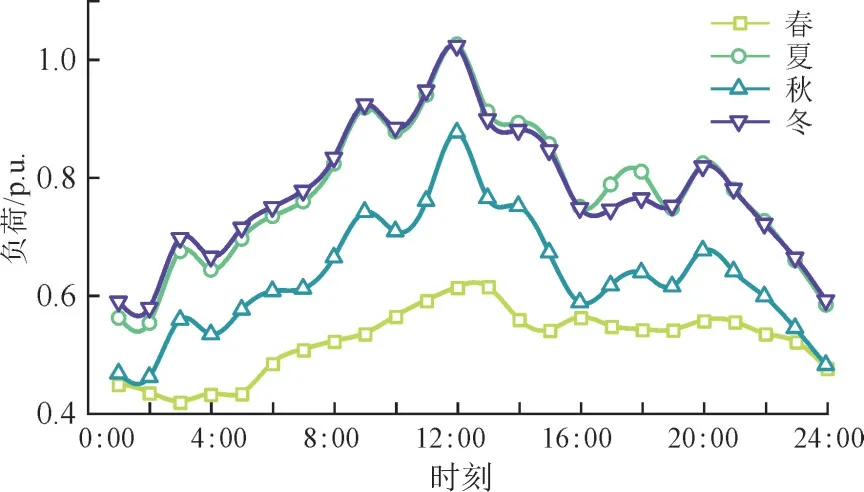
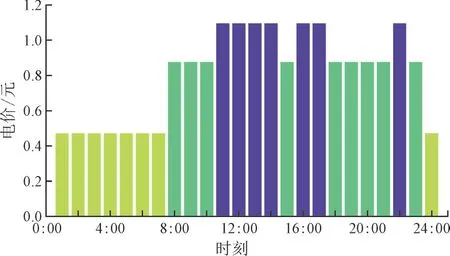
3.2 仿真结果及分析
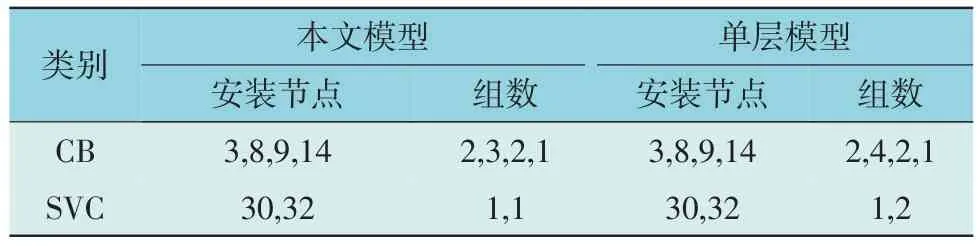
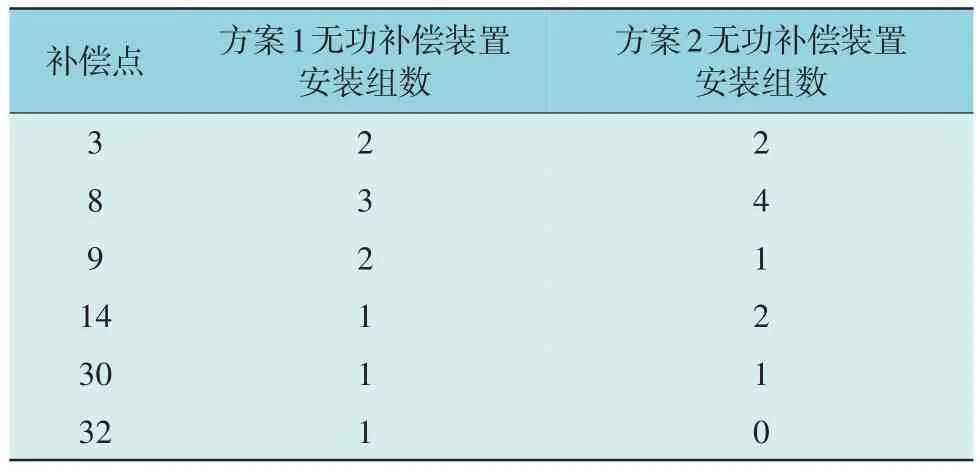
4 结论
