基于全寿命周期成本和综合故障率的油浸式变压器经济寿命评估

胡雪莹，李 琳

（新能源电力系统全国重点实验室（华北电力大学），北京 102206）

0 引言

电力变压器是电力系统一次侧主要设备，承担着电能转换的任务。变压器寿命通常分为物理寿命、技术寿命和经济寿命，物理寿命和技术寿命分别侧重于变压器内部绝缘状态和人为规定，经济寿命是根据变压器运行情况，从经济学角度预测其退运时间。电力变压器经济寿命预测可以给电力公司提供有效的更新决策，具有重要的工程实用价值。目前行业内尚没有关于变压器经济寿命的统一定义，而且传统的设备运行管理方式以一次投入成本大小为主要依据，存在片面性，不能满足资产管理要求。全寿命周期成本管理在上世纪八十年代引入我国，2000 年初在电网企业逐渐开始应用，将产品生命周期内发生的所有成本纳入计算，以发展的眼光看成本核算问题，能全面反映设备的长期投资成本，为后续经济决策提供数据支持[1]。

近年来，国内外学者开展了电气设备相关的全寿命周期成本（Life Cycle Cost，LCC）分类研究工作。文献[2]将LCC 成本模型分为静态成本和动态成本两大类，文献[3-6]对LCC 成本模型的分类几近相同，可概括为初始投资成本、运行成本、维护成本、故障成本、处置成本。针对电力变压器全寿命周期成本，在上述成本分类基础上，文献[7-8]提及了环境成本概念，文献[9-11]从检修角度分析了故障率对各类成本的影响，文献[12]则是利用存有设备历史信息的生存状态变量预测故障率以优化成本计算。

综上所述，变压器经济寿命评估主要分析了LCC 成本分类，但对环境成本的量化不够精确。此外，大部分文献中的LCC 成本模型难以兼顾长期投运过程中故障率的动态变化，仅有少部分文献在计算全寿命周期成本时单一考虑了设备运行历史信息或检修导致的故障率变化，缺乏对二者的有效结合。

本文在总结文献[1-12]研究的基础上，构建油浸式电力变压器全寿命周期成本管理体系，融入环境成本概念，同时结合2021 年全国首笔碳交易排放价格核算环境成本，更加完善地建立了油浸式电力变压器全寿命周期成本的组成成分，以考虑资金时间价值的全寿命周期成本等年值（Equivalent Annual Cost，EAC）最低为退运依据，建立油浸式变压器经济寿命模型。考虑油浸式变压器长期投运是一个动态过程，给出各类成本计算方法，描述了计及负载率、设备状态以及大修后役龄回退现象的综合故障率曲线，以有效利用设备历史信息和大修行为的综合故障率曲线作为经济寿命影响因素，帮助电力公司做出油浸式变压器更新决策。结合实际算例，得到3 次大修计划下最佳大修时间和相应的最低成本等年值，与2 次大修计划下结果对比，确定经济寿命，并分析各类成本在全寿命周期成本中的作用及其对经济寿命的影响。

1 油浸式电力变压器经济寿命模型

全寿命周期管理应遵循全系统、全费用、全过程三大原则，本文将设备从投入到退运的全部费用纳入全寿命周期成本，包括初始投资成本、运行成本、可靠性成本、处置成本四大类，具体如图1 所示。

1.1 全寿命周期成本的组成成分

1.1.1 初始投资成本

初始投资成本指变压器投运前的全部费用。工程造价一般取6.2%购置费作为安装调试费，取11.8%购置费作为其他费用，由此得到初始投资成本见式（1）：

1.1.2 运行成本

运行成本指变压器在役期间正常运行过程中以及为了维持变压器正常运行但不改变设备故障率产生的年度费用。即：

式中：t为投运年限，是设备当前投入运行的年龄，也被称为名义役龄；C2（t）为投运第t年的运行成本；C21（t），C22（t）和C23（t）分别为第t年的能耗成本、环境成本和维护成本。

能耗成本是变压器年电量损耗与上网电价的乘积，计算变压器年电量损耗时，认为无功充足，仅考虑有功损耗可表达为：

式中：q为年电量损耗；q0和qK分别为空载损耗、额定负载损耗；lf为平均负载系数；THPY为年运行小时，取8 760；P1是上网电价。

环境成本源于发电过程中化石燃料燃烧产生的温室气体。首先利用公式（5），明确发电每千瓦时以CO2为主的温室气体排放量及其排放价格，再从变压器超出损耗标准值[13]所对应的多余气体排放量入手，计算环境成本。即：

式中：Gfuel为按燃料比折合的发电每千瓦时温室气体等效CO2排放量；i为不同发电方式；θi，ηfuel,i，JT-D,i分别为不同发电方式下燃料比、能量转换效率、电网传输损耗；GCO2,i，GCH4,i，GN2O,i分别为不同发电方式下CO2，CH4，N2O的发电排放因子。

由于我国绝大部分电力由火力发电、水力发电供应，因此考虑以此2 种发电方式为代表，将表1 中数据代入式（5）得等效CO2排放量为7.4×10-4t/kWh[8]。

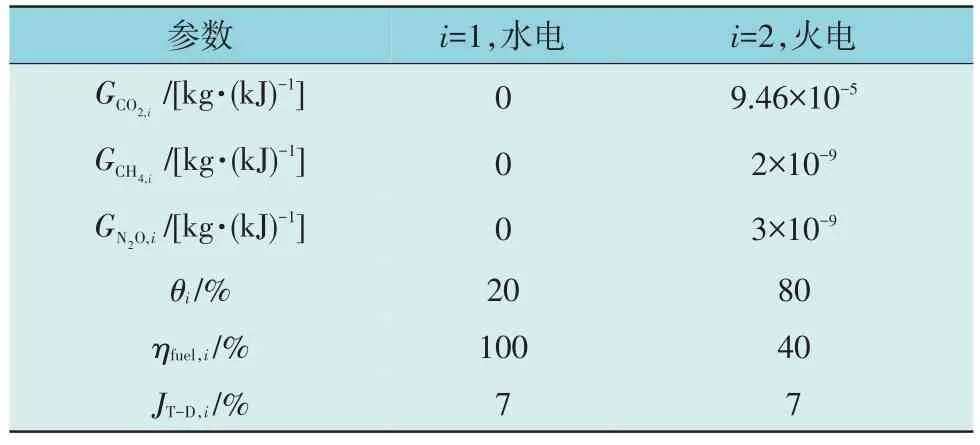
表1 等效CO2排放量计算参数Table 1 Calculation parameters for equivalent CO2 emissions

参考2021 年全国首笔碳交易价格52.78 元/t，得到CO2排放价格为0.039 元/kWh。由此，环境成本可表达为：

式中：qbz为变压器损耗标准值，qbz0和qbzK分别为同类型或同容量一级能效标准油浸式变压器的空载损耗和额定负载损耗；PCO2为CO2排放价格。

维护成本因设备维护而产生，是变压器小修、例行检查与维护的成本总和，其工作内容包括对变压器箱体及部件的检查和周期性污秽清扫、易损件更换等[14]。变压器小修、例行检查与维护每年一次，不改变设备故障率，维护成本可表达为：

式中：Kxx为基本小修成本，取购置费的1.5%；Klx为基本例行检查与维护成本；S（t）为设备等效役龄，与设备该时刻的性能相关，与投运年限一般不相符。

1.1.3 可靠性成本

可靠性成本指变压器在役期间为了降低设备故障率以提高其可靠性以及因设备故障、可靠性丢失需支出的费用。即：

式中：C3（t）为投运第t年的可靠性成本；C31（t）和C32（t）分别为第t年的大修成本和故障成本。

变压器大修是根据设备工况以及一定大修原则进行的解体方式检修，可以降低设备故障率，并非每年都要大修。其工作内容包括对设备内部铁芯与绕组的检修，对油箱及冷却系统的检查及器身外壳的清理工作等。在大修年份，大修成本可表达为：

式中：Kdx为基本大修成本，取购置费的6%；大修并不是每年进行，在无大修的年份取0。

故障成本是涉及故障率与故障后果的风险计算，对电力公司来说，停电会造成供电收入损失和额外的维修费用支出；对社会用户来说，停电会影响人们正常的生产生活，其负面社会影响是电价的数十倍。故障成本可表达为：

式中：λ[μHI,lf,S(t)]为综合故障率，其中μHI为归一化健康指数，从1 到0 代表设备性能由健康转为极不健康状态；a，b分别为考虑了变压器地区经济情况的单位时间可变维修成本和固定维修成本；tt为停机持续时间；S为变压器额定容量；cosφ为功率因数；P2为销售电价；Kd为电价折算倍数，代表停电的社会损失。

1.1.4 处置成本

处置成本指变压器退运时为了清理、销毁设备需支付的人工、设备费用。即：

式中：C4（L）为投运第L年时退运的处置成本；C41（L）和C42（L）分别为第L年的报废成本和剩余价值。

报废成本一般取安装调试费的32%，可表达为：

剩余价值采用直线折旧法计算[15]，可表达为：

式中：Z（L）为第L年时退运的剩余价值占比。

1.2 考虑资金时间价值的全寿命周期成本等年值

经济分析模式分为不考虑资金时间价值的静态模式和考虑资金时间价值的动态模式2 种[16-18]。全寿命周期成本是从投入到退运整个生命周期的总费用，由于资金时间价值的客观存在性，动态模式更适合于长期成本计算。本文选取退运年份作为基准时间，将各类成本按费用产生时间折算到退运年份，以成本等年值最低为目标建立经济寿命模型，即：

式中：CEA（L）为变压器投运第L年时退运的全寿命周期成本等年值；i为折现率，体现资金的时间价值，与通货膨胀等因素有关，取6%。

2 经济寿命模型的影响因素

2.1 计及负载率和设备状态的故障率曲线

变压器在额定负载条件、理想状态下运行的故障率曲线为基准故障率曲线。对于1 台实际变压器，并不能保持在理想工况下运行，随着投运年限的增长，设备内部的瑕疵或缺陷会逐渐显现[19-20]，且负载累计热效应也会对绝缘材料造成一定程度的损耗，使得其故障率不同于该时刻的基准故障率，即在一定负载系数、设备状态下的故障率曲线为实际故障率曲线，如图2 所示。

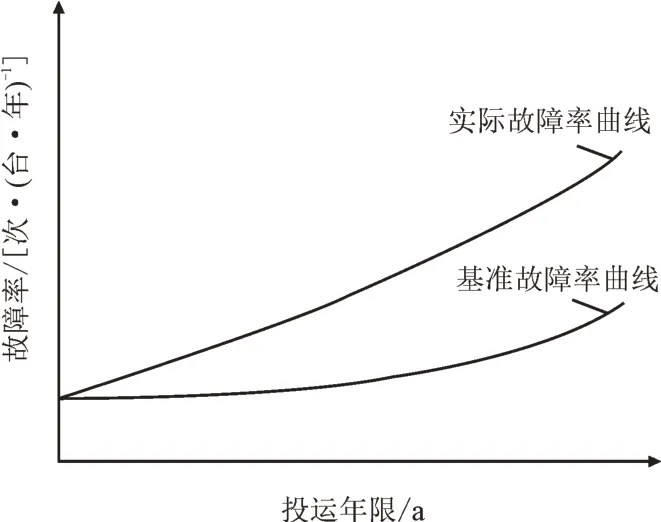
图2 实际故障率曲线与基准故障率曲线示意图Fig.2 Curves for actual failure rate and baseline failure rate

健康指数是定量描述变压器性能状态的参数，将其作为参量引入到温升老化失效模型，以负载率和设备状态为输入，可以在基准故障率曲线的基础上，得到存有设备历史信息的实际故障率曲线，由Arrhenius-Weibull-HI 模型[21-22]（后简称AWH 模型）表达，如式（17）所示。AWH 模型用威布尔分布表征故障率规律，既可以响应热老化造成的不可逆损耗，也可以响应可修复故障带来的故障率降低、寿命延长的效果。

式中：λ(μHI,lf,t)为实际故障率；β和L0分别为威布尔分布的形状参数和尺度参数，可根据变压器故障率历史数据进行拟合；m代表健康指数体系与设备期望寿命关系，本文中取为-3.677 1[22]；θHS,R为额定热点温度；FEQA（lf）为将服役时长划分成若干个区间Δths,i，由该区间内负载率lf决定、经热路模型下热点温度θhs,i(lf)折合得到的老化加速因子，是设备历史运行条件的体现[23-24]。

将式（18）代入式（17），即得投运年限为t时，以负载率曲线和设备健康状态为输入的故障率值。当FEQA（lf）=1、μHI=1 时，λ0（t）=β/L0（t/L0）β-1即为基准故障率曲线。

2.2 大修作用下的役龄回退现象

维护和小修能保证变压器正常运行，但不能降低设备故障率；大修能改善设备性能，降低设备故障率。大修后故障率仍遵循与之前相同的发展过程，单次大修作用下表现如图3 所示。

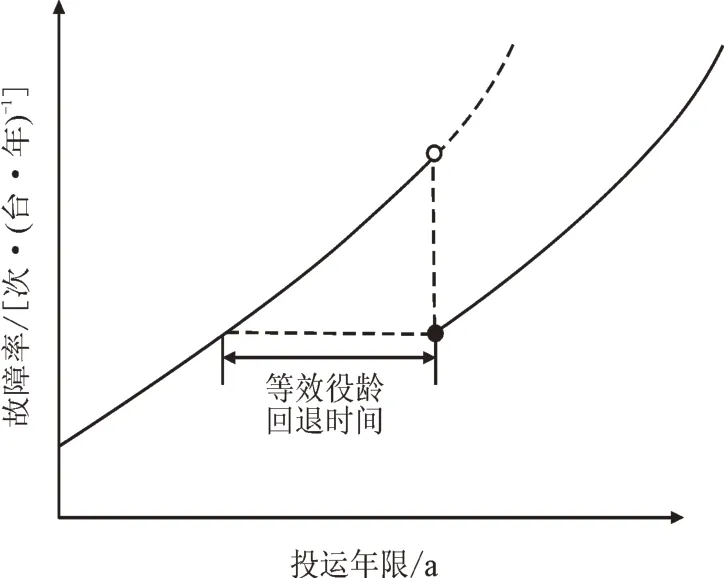
图3 单次大修作用下的故障率曲线示意图Fig.3 Curve for failure rate with a single overhaul

动态役龄回退因子可定量描述多次大修对设备性能的修复效果，且随着大修次数的增加，大修效果逐渐下降。大修导致的役龄回退和多次大修后等效役龄关系如式（19）和式（20）所示[10]：

式中：α为动态役龄回退因子；Δti为第i次大修后役龄回退时间；t1，t2，t3分别为3 次大修时间。

变压器在不同负载率及设备状态下工作时，故障率曲线由基准故障率曲线转为当前实际故障率曲线；而大修则能改善设备性能，使变压器等效役龄代替投运年限，故障率曲线在实际故障率曲线的基础上又有所下降，转为大修后的综合故障率曲线，如图4 所示。

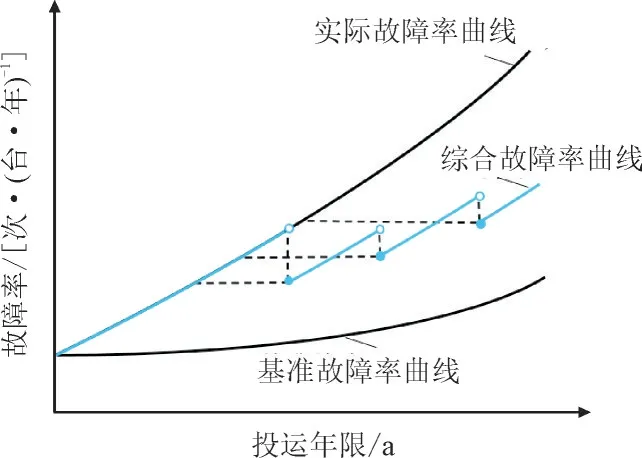
图4 综合故障率曲线示意图Fig.4 Curves for comprehensive failure rate

图5 经济寿命评估流程Fig.5 Evaluation process for economic life

综合故障率曲线可表达为：

3 基于粒子群算法的大修决策优化

3.1 粒子群算法

粒子群算法由Eberhart 和Kennedy 于1995 年首次提出，是一种模拟自然生物群体行为的优化技术，具有思想直观、简单、收敛速度快等特点[25]。其基本概念来源于对鸟群觅食行为的研究，当一群鸟在随机搜寻食物时，找到食物的最简单有效策略就是每只鸟不断搜索自己周围区域的食物并将信息共享，进而使得群体找到最多食物的区域[26]。鸟就是粒子群算法中的粒子，每只鸟即每个粒子都有自己的位置和速度，还有一个关于目标函数的适应度，通过比较粒子适应度的个体最优值和群体最优值，获取粒子最优位置。

若种群由n个粒子组成，当i=1，2…n，和分别为第i个粒子第k次迭代时的位置和速度，pi为第i个粒子的历史最优位置，pg为群体中所有粒子的当前最优位置，粒子速度和位置迭代过程表示为：

式中：c1和c2分别为个体和群体学习因子；r1和r2为[0，1]范围内的随机数；ωmax和ωmin分别为惯性权重的最大值和最小值；D为最大迭代次数。

ωmax-（ωmax-ωmin）k/D代表第k次迭代时惯性系数的更新，线性递减的参数设置方法利于粒子群在全局和局部搜索之间取得平衡[27]。

3.2 大修决策优化

多次大修时间不是随意决定的，大修不仅会使等效役龄小于投运年限，还会进一步影响变压器综合故障率。粒子群算法可以从大修决策的随机解出发，取1.2 节中全寿命周期成本等年值函数值为适应度，在迭代寻优确定大修时间的同时，得到最低全寿命周期成本等年值，完成变压器经济寿命评估。

4 实例分析

4.1 基本信息

以1 台油浸式电力变压器为例，结合本文模型对变压器经济寿命进行评估。变压器相关参数见表2。

由于当前变压器故障率统计数据较为匮乏，历史负载记录和设备状态难以回溯，根据已有运行经验，取变压器的基准故障率为式（23）[28]，μHI在偶然故障期为1，在损耗故障期为多台变压器健康指数的加权值0.935 4[22]。根据实际运行环境温度与1.1 倍负载条件，该变压器四季热点温度曲线如图6 所示，并经式（18）计算四季老化加速因子，进而得到年老化加速因子FEQA（lf）=1.423 4，考虑大修后的等效役龄，变压器综合故障率曲线见式（24）：

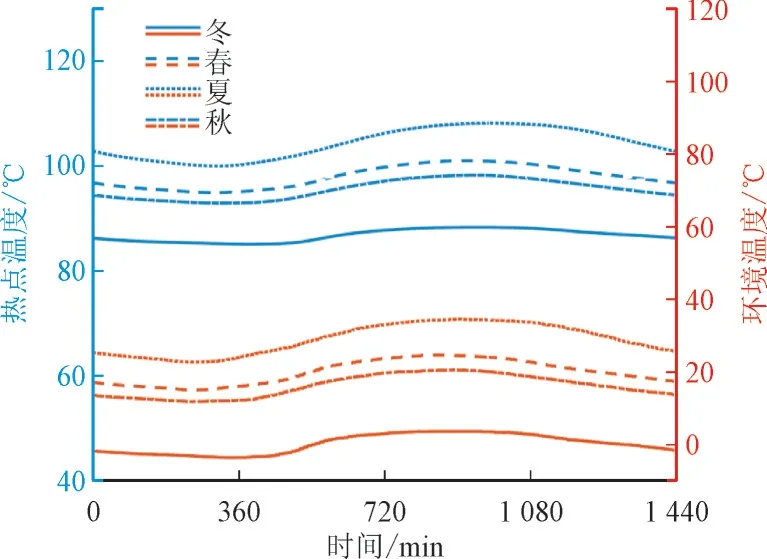
图6 变压器温度曲线Fig.6 Temperature curves for transformer

将表2 中数据代入式（1）—式（16），经粒子群算法对大修决策优化，可得在投运第L年时退运的最低变压器全寿命周期成本等年值，完成经济寿命评估。2 次、3 次大修计划下最佳大修时间和相应的最低成本等年值结果如表3 所示。其中，粒子群算法的参数为：粒子群规模30，迭代次数100，自我学习因子和群体学习因子均取1.4，惯性权重在迭代过程中从0.9 线性减小到0.4，粒子群优化过程如图7 所示。

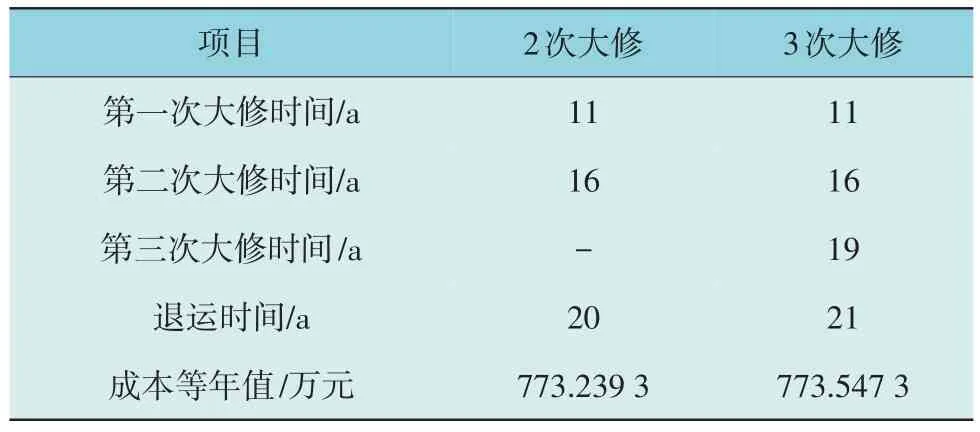
表3 变压器经济寿命评估结果Table 3 Economic life evaluation results of transformer

图7 粒子群优化过程Fig.7 Optimization process by PSO

4.2 结果分析

4.2.1 大修决策优化及故障率曲线

由表3 和图8 可见，该变压器在投运第11 年、16 年、19 年的3 次大修决策下，于21 年末退运，最低成本等年值为773.547 3 万元。若该变压器投运21 年后持续运行，其成本等年值会迅速增加，经济效益会持续降低。

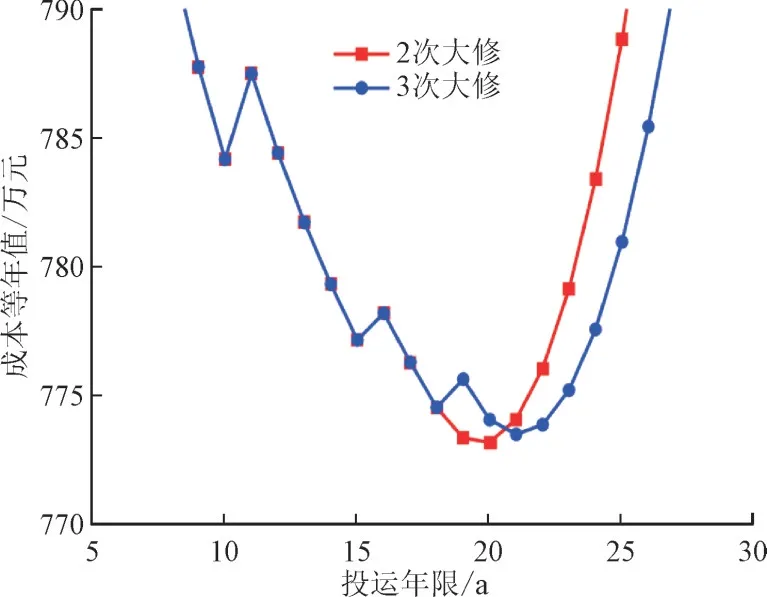
图8 成本等年值随投运年限变化曲线Fig.8 Curves for change in EAC with operation years

此外，不得不提的是该变压器在投运第11 年、16 年的2 次大修决策下，于20 年末退运，最低成本等年值为773.239 3 万元。2 次大修决策下最低成本等年值约等于甚至低于3 次大修决策下最低成本等年值，宜采用2 次大修。图9 为各类故障率曲线，由图9 可知，随着大修次数的增加，大修效果逐渐下降，大修导致的故障率降低在投运后期不明显，对应的故障成本减少不能抵消单次大修成本的增加。由此可见，适量次数的大修经决策优化确定时，可以提升变压器经济效益，当大修次数过多时反而会降低经济效益。

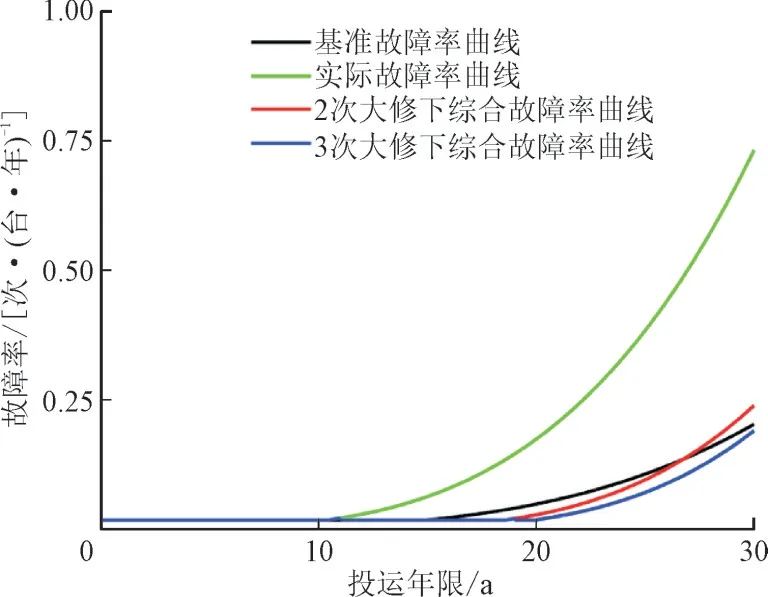
图9 各类故障率曲线Fig.9 Curves for various failure rate

4.2.2 各类成本对成本等年值的影响

在大修年份时，对于可靠性成本，大修成本支出使得其数额增加；对于运行成本，大修后设备性能改善，役龄回退、故障率降低，使得其下一年数额减少。由此，大修成本支出及其役龄回退现象造成了图8 中3 次大修时变压器投运第11 年、16 年、19年的成本等年值波动。

除了大修年份时成本等年值的局部波动，成本等年值整体趋势先减小后增大。这主要是因为投运前期初始投资成本在成本等年值计算中占据了主导地位，随着投运年限增加，初始投资成本分摊到各年的数值变小，使其变小；在投运后期，运行成本和可靠性成本在成本等年值计算中占据了主导地位，随着投运年限增加，大修次数变多，运行成本和可靠性成本分摊到各年的数值变大，使其变大。

5 结语

电力变压器是电网中的重要设备，对其进行寿命分析十分必要，经济寿命评估可以帮助电力企业完成精益化管理。本文依托于全寿命周期成本管理，阐述了变压器从投入到退运所需计算的各类成本及其表达式，以成本等年值最小为目标建立了经济寿命模型，并进行了模型算例求解。此外，在油浸式变压器经济寿命模型的计算过程中，本文分析了影响经济寿命的故障率曲线，并以粒子群迭代优化大修决策为手段，确定设备经济寿命、给出该经济寿命下的设备最低成本等年值及相应大修时间，对变压器更新决策有一定指导作用。