基于VPP碳流计算的多目标多时间尺度优化调度
2024-01-28于东民王晓鹏孙钦斐杨晓辉刘华南
于东民,王晓鹏,孙钦斐,杨晓辉,刘华南
(1.南昌大学信息工程学院,江西南昌 330031;2.国网北京市电力公司,北京 100041)
0 引言
在当今社会,能源消费结构的转型、新型能源的开发利用以及能源利用的低碳化等问题已经成为了广泛关注的热点话题[1-2]。面对日益严峻的能源和环境问题,分布式能源以其高效、清洁等优势而受到重视。在此背景下,虚拟电厂(Virtual Power Plant,VPP)作为一种整合型分布式电力系统,通过将不同类型的分布式能源整合起来,利用多能互补促进新能源消纳,突破了分布式能源数量差异化、位置分散化、发电间歇性等限制[3-4],提高了其参与市场竞争的能力。
目前,VPP 低碳经济运行的研究已取得了一些进展。文献[5]引入“碳交易-绿证”交易模型,以最小化运行成本和源侧碳排放构造多目标优化模型,并采用“参照点法”进行求解。文献[6]应用电转气和碳捕集耦合模型,从源侧出发应对VPP 碳排放问题,并提出了协助新能源消纳的VPP 优化调度策略。然而,文献[7-8]指出,在多能互补系统中,碳排放计量不应仅针对源侧,而应从“碳视角”审视整个能源流动过程,使系统受众对碳排放承担相应责任,并据此原则提出了碳排放流计算模型。同样,文献[9]也指出,利用碳排放流计算模型引导用户改变其用能行为,是一种以碳为主导的能源系统优化运行方式。然而,目前对VPP 碳排放流的研究还存在以下问题:首先,现有文献很少直接研究VPP 碳排放流计算模型,而在多能互补系统中常以输入侧碳排放因子和能源分配比为基础,结合能源枢纽模型进行碳排放计算[10-11]。而对于VPP 内部的储能设备、碳捕集等影响单时段碳流守恒的设备却没有建立准确的模型,导致在计算输入碳流的精度时存在误差,从而降低了VPP 低碳化运行效益。其次,建立碳流计算模型时引入碳流密度将使模型呈现出强非线性特征,模型求解存在一定的难度。
此外,可再生能源和负荷等不确定性因素对VPP 优化运行的影响也是一个重要的问题[12-13]。近年来,多时间尺度优化调度方法已被广泛应用于电力系统不确定性因素的处理。文献[14]提出了一种基于日前-日内的多时间尺度优化调度模型,指导VPP 集群进行市场交易和能流管控。文献[15]基于“多级调度、逐级细化”的原则,提出了一种日前优化、日内滚动的VPP 多时间尺度优化调度策略。文献[16]提出了一种基于鲁棒随机优化的VPP 多时间尺度优化调度策略,修正日前调度计划,以应对不确定性的影响。
综上所述,现有研究较少综合考虑多时间尺度、碳排放流计算和VPP 低碳经济运行,以提升VPP 综合运行效益。为此,本研究提出了一种基于VPP 碳流计算的多目标多时间尺度优化调度策略。在日前调度阶段,建立VPP 能流、碳流计算模型,并基于此提出VPP 低碳经济运行策略,利用归一化法向约束(Normalized Normal Constraint,NNC)法求解该非线性多目标规划模型;在日内调度阶段,利用动态矩阵控制(Dynamic Matrix Control,DMC)算法的原理,通过跟踪日前调度计划,建立状态空间矩阵进行求解,再执行反馈校正形成闭环控制。
1 虚拟电厂结构
VPP 结构如图1 所示,由风机(Wind Turbine,WT)、光伏(Photovoltaic,PV)、电储能系统(Electricity Storage Systems,ESS)、碳捕集系统(Carbon Capture System,CCS)、热电联产(Combined Heating and Power,CHP)、燃气锅炉(Gas Boilers,GB)和电锅炉(Electric Boiler,EB)组成。
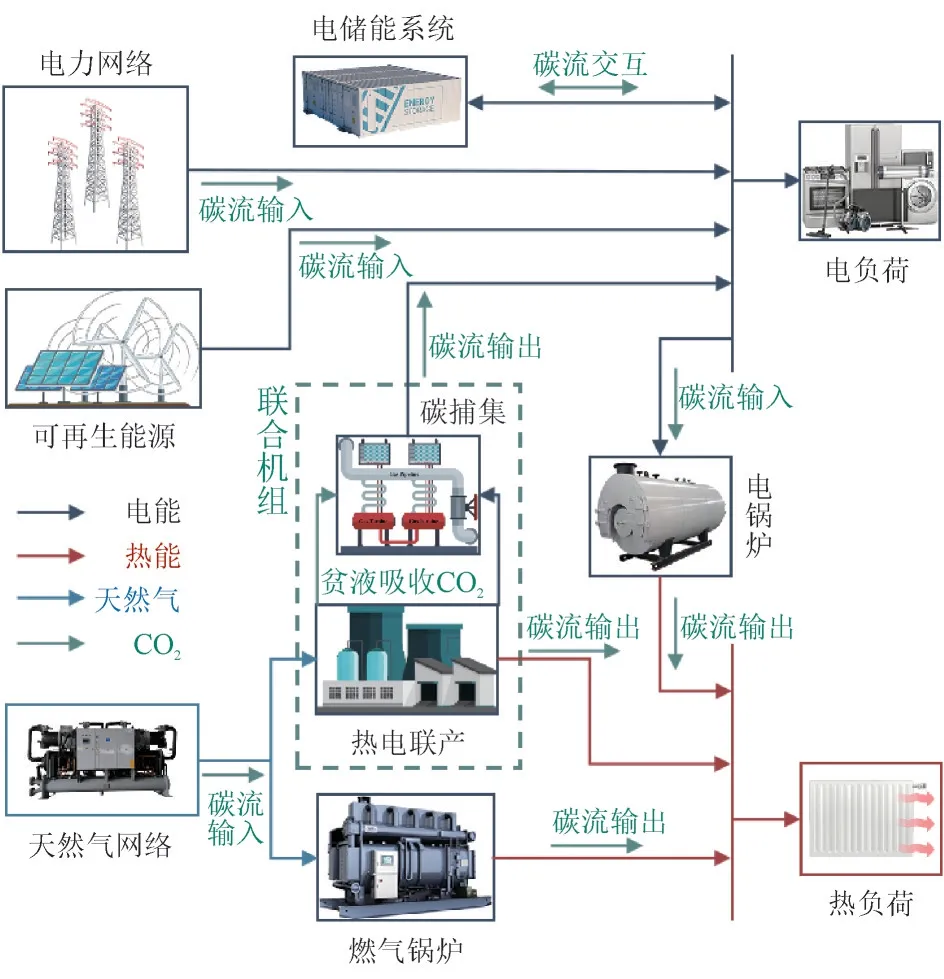
图1 虚拟电厂结构Fig.1 Structure of virtual power plant
1.1 虚拟电厂能流模型
为了建立VPP 能流模型,首先对VPP 设备建模。按照能量转换关系将VPP 内部设备分为双向耦合设备(如ESS)、输入端设备(如PV,WT)、单输入单输出设备(如GB,EB)和单输入多输出设备(如CHP)。为了便于碳流计算,将依附于CHP 的CCS归为CHP 中组成联合机组,并将其归为单输入多输出设备。
1)双向耦合设备
ESS 的能流运行方式为:
2)输入端设备
可再生能源系统的能流运行方式为:
3)单输入单输出设备
单输入单输出设备的能流运行方式为:
4)单输入多输出设备
对于CHP,其工作方式为:
而对于CCS,本文采用溶剂存储方式对CCS 进行建模,通过富液、贫液存储罐,将碳捕集和碳分离2 个过程进行解耦[17]。CCS 满足以下运行方式:
VPP 在安装CCS 后,CHP 将为CCS 供能,而CCS 吸收CHP 在供能过程中所产生的CO2,二者由此组成联合机组,其运行方式为:
式中:Ptn 为t时刻下联合机组的净出力;ρgas为天然气网络向VPP 输送天然气支路的碳流密度;分别为碳捕集水平的上、下限;γCCS为烟气分流比。
根据VPP 设备模型,可以建立能流模型以描述VPP 内部能源耦合关系,并便于辨识VPP 内附于能流的碳流走向。VPP 能流模型具体为:
1.2 虚拟电厂碳流模型
在电力系统中,碳流计算需要根据能流计算结果展开,通过设定碳排放流将VPP 的碳排放引入至负荷侧,以定位和追踪碳排放的流向[18]。根据前人所提碳流计算理论[19],结合VPP 内部结构,建立VPP 碳流计算模型,具体为:
1)单输入单输出模型
2)单输入多输出模型
联合机组的碳排放流向如图1 所示,根据碳排放量守恒原则,则有
由于支路碳流密度与其效率成反比[20],即:
结合式(19)和(20),则有:
由于CHP 还需为CCS 供电,根据碳排放量守恒原则,得到联合机组发电支路的输出碳流率为:
式中:为t时刻下联合机组发电支路的碳流密度。
3)双向耦合设备
ESS 充电相当于负荷,吸收部分CO2;而放电充当电源,此时ESS 外排碳流取自于自身所储能量。为此,引入“碳荷率”的概念,表示ESS 内碳排放量与其对应的储电量之间的比值,即每度电可等效产生多少碳排放量。ESS 充放电的碳流计算方式为:
由VPP 设备碳流计算方式,并依据文献[21]中描述的节点碳势与支路碳流密度关系,可以建立VPP 碳流计算模型,具体如式(28)所示:
式中:和为t时刻下电负荷和热负荷侧的支路碳流密度;ρres和ρgrid分别为可再生能源系统发电支路和上级电网输送电能支路的碳流密度。
2 日前多目标优化模型
基于所建立的能流、碳流模型,就日前调度阶段提出了VPP 多目标优化模型。设定运行周期为24 h,时间间隔为1 h,优化目标为最小化运行成本和碳排放量,并采用NNC 法求解该非线性多目标规划问题。
2.1 VPP经济性评价函数
VPP 的综合运行成本F1为:
式中:和分别为t时刻的燃料成本和维护成本。
1)设备维护成本
式中:RPV,RWT,RCHP,REB,RGB,RESS和RCCS分别为PV,WT,CHP,EB,GB,ESS 和CCS 的单位运行维护成本。
2)燃料成本
2.2 VPP环保性评价函数
以碳流计算为基础,从负荷侧入手制定VPP 低碳运行准则,即设置最小化负荷侧碳流量为第二个目标函数F2:
2.3 归一化法向约束法
NNC 法在求解非线性多目标优化问题的效率较高、收敛性较好[22],求解其步骤为:
1)锚点:针对2 个目标函数Z1,Z2分别执行单目标优化,获得各目标函数的最优解和相对的另一个目标的函数值,即得到解,这2 组解构成帕累托前沿解空间的2个极端点。
2)规格化:以2 个目标函数为坐标轴,分别按照式(33)的方法,对帕累托前沿解空间进行规格化,其过程的示意图如图2 所示。

图2 解空间规格化Fig.2 Solution space regularization
式中:和分别为2 个目标函数规格化后的值。
3)定义交点:定义乌托邦线上的向量为,并将乌托邦线NZ等分,得到乌托邦线上出现NZ+1 个等距分割点Ai,i∈{1,…,NZ} 。在第i个分割点处做垂直于乌托邦线的垂线,并规定其向量为,此垂线与帕累托前沿的交点为Bi。
4)添加约束条件:定义原点指向点Ai和点Bi的向量分别为和。此时以Z2为主要目标函数,添加为约束条件,构造单目标优化问题,即可求得此时帕累托前沿对应的最优解Bi。该单目标优化问题的解空间为图2 中所划分的完整解空间的上半部分。
5)反复求解:i=i+1,然后重复步骤4,将每个等距分割点求解,最终得到完整的帕累托前沿。
3 日内动态优化模型
在日内动态优化阶段,设定控制时域为45 min,时间间隔为15 min,以日内超短期预测数据为输入,通过跟踪日前优化结果,并采用基于DMC 算法的有限时域优化策略进行日内调度和实时决策。
基于DMC 算法的有限时域优化策略是一种含有反馈校正环节的闭环调度模式[23],可以更好地应对不确定性。基于DMC 算法的有限时域优化如图3所示,其步骤为:(1)当t=t1,基于t时刻的实时反馈值求解日内优化调度模型,得到控制变量在控制时域内的控制序列(如图3 中浅色阴影),并下发t+Δt时刻的值;(2)时间向前推进Δt,即t=t2=t1+Δt,此时完成实时决策,并根据实际运行情况执行实时反馈校正(如图3 中深色阴影),更新t时刻的实时运行参数并作为反馈值用于下一步优化;(3)令t=t2,重复步骤1,直到完成整个周期的优化调度。
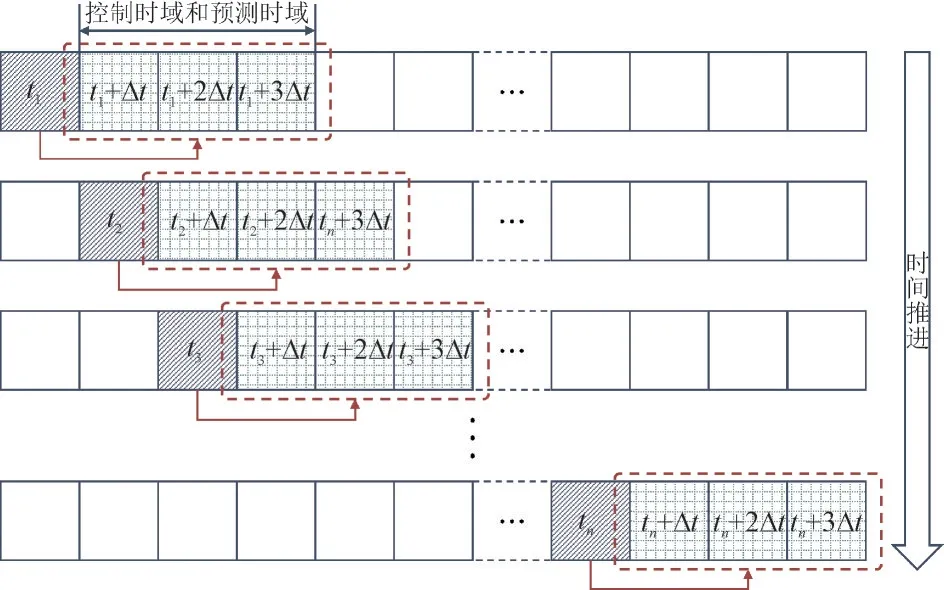
图3 基于DMC的有限时域优化Fig.3 Finite-time-domain optimization based on DMC
3.1 DMC有限时域优化模型
本文基于DMC 算法建立的日内有限时域优化空间状态模型为:
3.2 实时决策和实时反馈校正
由于实时数据与超短期预测数据之间仍存在较小的偏差,当下发控制序列的第一个值后,需要执行实时决策[24]。该环节通过VPP 与上级电网的交互行为维持VPP 实时运行的能源供需平衡。采用DMC 算法的日内优化需要前一时刻的实时运行值为基础值,以前一时刻的值影响后一时刻,从而形成闭环优化,避免放大日前预测偏差[25],其具体方法为:
4 算例仿真与分析
4.1 基础数据
本研究以华东地区某VPP 为研究对象,取冬季某典型日数据。系统运行相关参数如表1 所示。风光出力及负荷需求的日前预测信息,购电分时电价信息如图4 所示。本研究通过MATLAB 调用YALMIP工具箱构建模型,并采用Gurobi 求解器求解。

表1 VPP运行相关参数Table 1 Related parameters of VPP operation
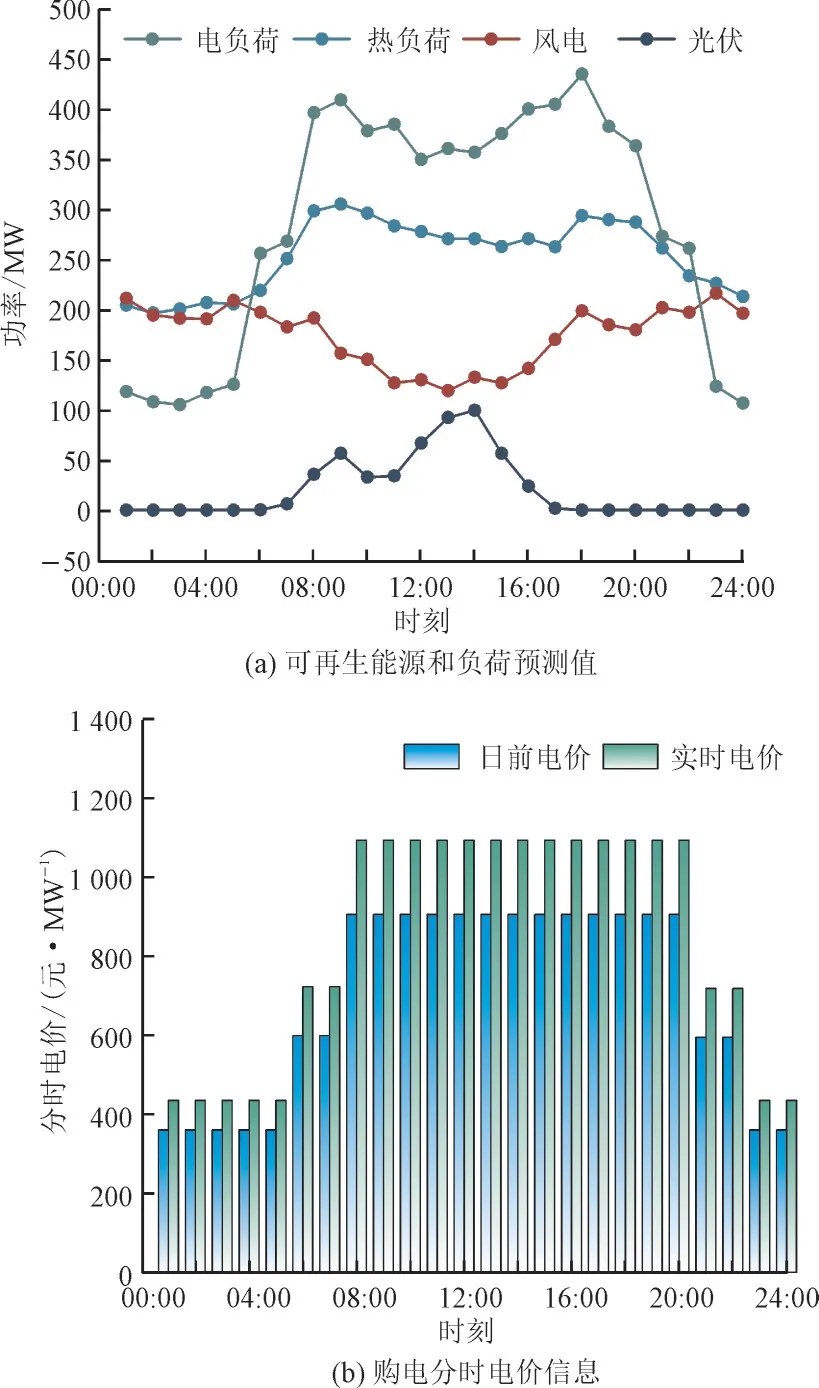
图4 日前预测值和购电电价Fig.4 Day-ahead forecasts and time-of-use tariffs
4.2 日前优化效益分析
4.2.1 NNC法求解效益
为凸显所提多目标模型求解算法的优势,将NNC 法与传统的NSGA-II 算法进行对比。2 种求解算法所形成的帕累托解集如图5 所示。可见,利用传统的启发式算法求解高维度非线性多目标问题时,虽然其非支配解拥有更广的决策分布,但是其分布不均匀且难以收敛至可行域的凸边界等缺点也一览无遗。此外,对比两者的优化性能可以发现,虽然NSGA-Ⅱ算法的最优解相比于NNC 法的最优解提升了经济运行效益,但却落后了环保运行效益。综上所述,验证了NNC 算法的有效性。
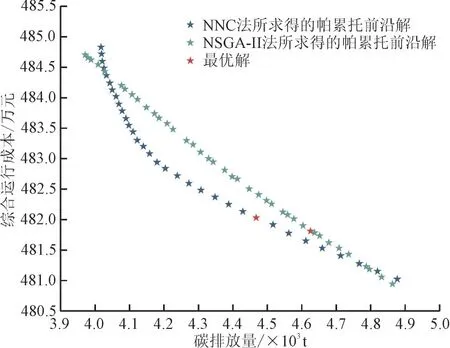
图5 帕累托前沿解Fig.5 Pareto solution set
4.2.2 多目标优化效益
本文基于VPP 能流和碳流模型设置了3 种不同的日前优化策略。其中,策略1 为所提多目标优化模型,策略2 为仅考虑经济性的单目标优化对比模型,策略3 为仅考虑环保性的单目标优化对比模型。
如表2 所示,利用熵权-TOPSIS 法,得到非支配解分布所反映的信息。其中,“综合运行成本”维度的信息熵值较低,意味着其变异程度较高,因此其信息效用值也呈现较高的水平,说明VPP 调度计划主要影响VPP 运行的经济效益。其次,经过熵权法的计算,发现碳排放量所占权重将近40%,说明VPP 调度计划对VPP 碳排放的影响也不容忽视,这突出了在制定VPP 调度计划中考虑多目标优化的重要性。

表2 非支配解分布所呈现的信息Table 2 Information presented by distribution of non-dominated solutions
另一方面,通过对比3 种策略的优化性能,同样突出了考虑多目标优化的重要性。如表3 所示,策略2 和策略3 在其所指定目标上的表现均较为突出。例如,策略2 的经济性最佳,而策略3 中CO2排放量和弃风弃光量相比于策略1 降低了10.09%和18.68%。然而,在其非指定目标上,单目标优化模型的表现效果极差。例如,策略2 的弃风弃光量高达203.92 MW,超过策略1 弃风弃光量的2 倍。相较而言,策略1 虽然在每项运行效益上达到次优水平,但这恰恰体现了决策时的均衡思想,以追求从整体上提升VPP 综合运行效益。
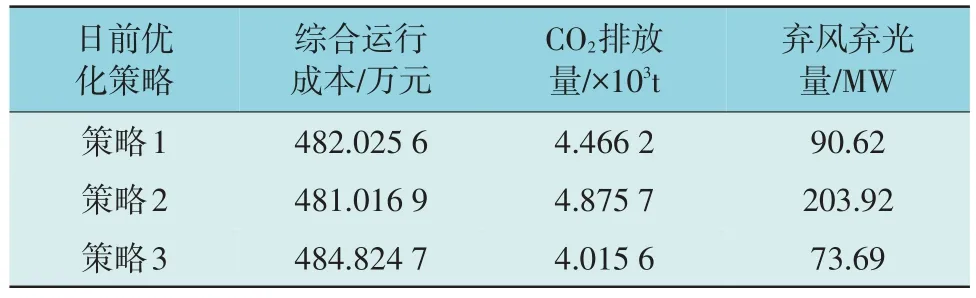
表3 3种日前优化策略的优化性能Table 3 Optimization performance of three day-ahead optimization strategies
4.2.3 日前碳流计算校验
为了展示VPP 碳流计算模型的有效性并验证碳流计算精度,图6 展示了策略1 下18:00(峰时段)和24:00(谷时段)2 个时段内VPP 碳流率分布情况。可见,在谷时段,联合机组碳流率较低,这是因为可再生能源的碳流密度较低,所以通过增发可再生能源出力,使CHP 增发对CCS 的供能,从而降低联合机组发电测输出碳流率。反观峰时段,VPP将优先满足负荷需求,加大了外来能源输入和增发分布式能源的出力,使得各支路碳流率显著增大。根据负荷侧碳流率从谷时段的10.763 5 t/h 增加到169.583 5 t/h 的变化情况,恰好对应于该分析结果。在实际应用中,这方便于调度员从负荷侧统计到VPP 的碳排放情况。

图6 VPP的碳流分布Fig.6 Carbon flow distribution in VPP
由图6 可以看出每个时段下VPP 的输入碳流与输出碳流之间显然不平衡,这是由于ESS 和CCS的存在使得VPP 不再满足单时段碳流守恒原则,而是变成周期内碳流守恒原则。通过计算,典型日周期内输入碳排放量和输出碳排放量均为4 466.2 t,碳流计算精度为99.99%。
4.3 日内优化效益分析
4.3.1 基于DMC算法的优化模型性能分析
为验证所提有限时域优化模型的有效性,对比了3 种日内预测精度下2 种日内优化模型的性能。假设VPP 的实时运行数据为日前预测数据的±12%,而3 种精度下日内超短期预测信息分别为日前预测数据的±3%,±6%和±9%,预测精度逐步提升。2 种日内优化模型分别为模型(a)传统开环动态优化;模型(b)基于DMC 的闭环动态优化。2 种模型采用的日前优化模型一致。2 种模型的运行效益对比如表4 所示。

表4 对比不同日内优化模型的性能Table 4 Comparison of performance between different intraday optimization models
如表4 可以看出,同一预测误差下,所提日内优化模型在实时运行性能上均优于对比模型,且随着日内预测精度的提升,所提模型的优势不减,这验证了所提模型的有效性。而在跟踪日前调度计划上,如图7 所示,虽然在线开环优化模型仅以日前调度计划为基础值,具有更符合日前全局最优解的优势,但相比之下所提模型的跟踪效果并未极大落后于在线开环优化模型,突出了所提在线优化模型具有更强的适应性。

图7 不同的在线优化模型的跟踪效果Fig.7 Tracking effect of different online optimization models
4.3.2 校验实时碳流计算
由于日前预测数据与实时运行数据之间存在预测误差,因此有必要检验碳流计算模型在预测误差的影响下是否能够保持稳定。如表5 所示,虽然碳流计算模型的实时精度会随着预测误差的增大而减小,但3 种预测误差情景下实时精度均超过95%,能达到要求,再次验证了碳流计算模型的有效性。
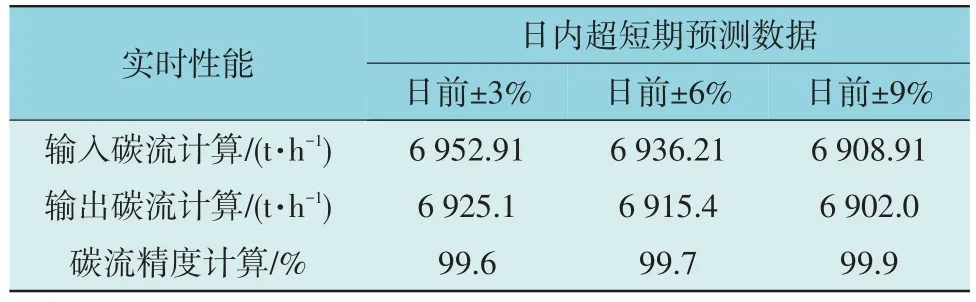
表5 不同预测误差情景下碳流计算模型的实时精度Table 5 Real-time accuracy of carbon flow calculation models in different prediction error scenarios
5 结论
本研究提出了一种基于VPP 碳流计算的多目标多时间尺度优化调度策略,以综合性提高VPP 运行的经济性、环保性和可再生能源消纳能力。通过仿真分析和对比实验,结果表明:
1)建立VPP 碳流计算模型,并基于此提出VPP低碳经济运行策略,经仿真结果检验,碳流精度均满足95%的基本要求,并验证了所提模型的有效性;
2)考虑VPP 运行的经济、环保效益,建立VPP日前非线性多目标优化模型,利用NNC 法和熵权TOPSIS 法进行求解,结果表明有效地从整体上提升VPP 综合运行效益;
3)针对不确定性因素,利用基于DMC 算法的动态日内优化策略,其结果在经济性、环保性等方面相比于传统日内优化模型具有一定优势,并实现对日前计划的有效跟踪,满足系统实时运行需求。
