Hadamard分数阶积分的Volterra-Fredholm型时滞积分不等式

韩晓月, 徐 润

(曲阜师范大学数学科学学院,273165,山东省曲阜市)

0 引 言

在过去的几十年里,分数阶微积分已经应用于许多研究领域. 关于分数阶积分不等式也得到了许多的研究成果,比如文献[1-12],其中关于Volterra-Fredholm型积分不等式是一个重要的课题.

1992年,文献[1]研究了以下最早的 Volterra-Fredholm 型积分不等式

2002年,文献[2]将上述不等式进行了推广,研究了如下不等式

2004年,文献[3]研究了具有两个自变量的线性 Volterra-Fredholm 积分不等式

2008年,文献[4]研究了非线性时滞 Volterra-Fredholm 积分不等式

随后的研究进一步推广了 Volterra-Fredholm 积分不等式及其应用[5-10], 其中,2018年,文献[8]研究了如下非线性 Volterra-Fredholm 型分数阶积分不等式

2022年,文献[10]研究了关于Riemann-Liouville分数阶积分的非线性 Volterra-Fredholm型积分不等式

受上述工作的启发,本文建立了关于Hadamard分数阶积分的含有单变量和双变量的非线性 Volterra-Fredholm 型积分不等式.

1 相关定义

定义1.1[13]一元函数f(t)的α阶左定、右定Hadamard 分数阶积分定义为

定义1.2[14]二元函数F(x,y)的 Hadamard 分数阶积分定义如下,

2 主要结果及其证明

2.1 含有 Hadamard 分数阶积分的一元函数不等式

在下面的讨论中,假设各函数满足以下条件:

(ⅰ)x(t),f(t),c(t),pi(t),si(t),hi(t),r(t)∈C([a,b],+) (a>0),并且r(t)≤t,i=1,2,…,k,k∈+;

(ⅲ)c(t),r(t),hi(t),i=1,2,…,k,k∈+是增函数,且hi(t)≥1;

1<α<2时,考虑以下2个积分不等式.

(1)

(2)

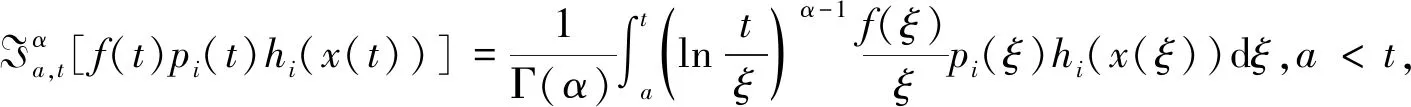
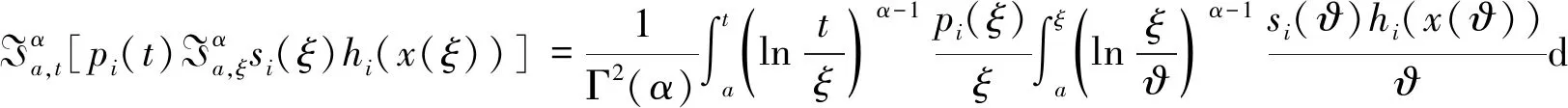
定理2.1如果x(t)满足式(1),则

(3)

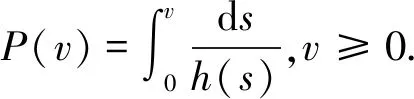
证明显然式(1)可写成

因此有

(4)

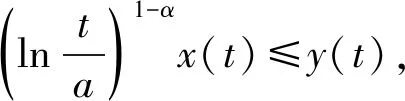
(5)

根据假设(ⅲ)可得h(t)单调递增,故

由此可得

(6)

令t=τ,式(6)两边对τ从a到t积分,由y(a)=0得

又因为P是单调递增的,并且y(a)=0,所以有

(7)

由式(5)和式(7)即可推出式(3)成立.

定理2.2如果x(t)满足式(2) ,则

(8)

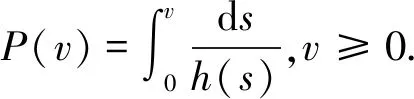
证明将式(2)写成如下形式

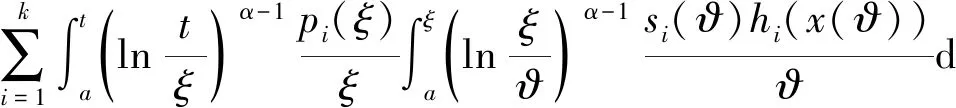
由此得

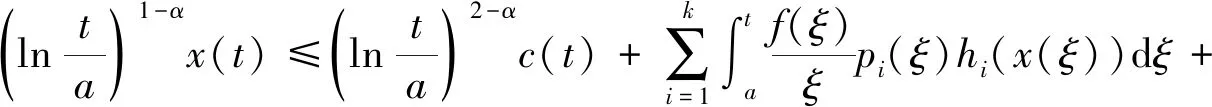
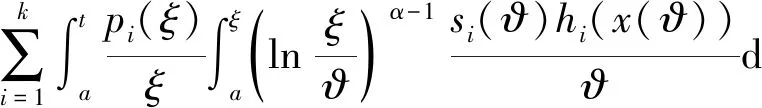
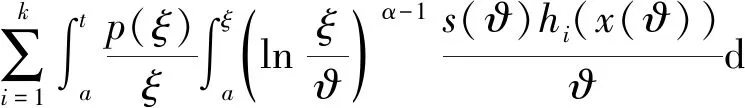
(9)

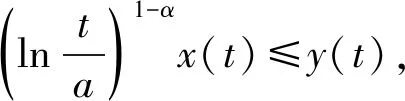
(10)

由假设(ⅲ)可知h(t)单调递增,故y′(t)(t∈[a,b])满足

因此

(11)

类似于定理2.1的证明,由y(a)=0可得

因为P是单调增函数,y(a)=0,所以

(12)

由式(10)和式(12)可得式(8).

下面研究关于Hadamard分数阶积分的Volterra-Fredholm型时滞积分不等式.

定理2.3设W(t)=P(2t+c(b)-2c(a))-P(t)是增函数. 如果x(t)满足

(13)

则

(14)

这里1<α<2.

证明根据式(13)可得

定义上式右端为一个新函数y(t),则y(t)单调递增,且x(t)≤y(t),y(b)=c(b)+2(y(a)-c(a)).由假设(ⅲ)可知h(t)单调递增,故

类似于定理2.1的证明可得

(15)

因为P是单调递增的,所以

(16)

把t=b代入式(15)即得

(17)

因为W(y(a))=P(2y(a)+c(b)-2c(a))-P(y(a))=P(y(b))-P(y(a)),所以由式(17)可得

又因为P和W均为增函数,所以

(18)

由式(16)、式(18)可得

(19)

由x(t)≤y(t)和式(19)可得式(14) .

注1. 若令上述定理中h(t)=t+1,并且c(t)满足c(b)≤2c(a)+1,根据函数P、W的定义,有P(v)=ln(v+1),W(t)=ln(2t+c(b)-2c(a)+1)-ln(t+1),P、W均为增函数.

2. 同样,若令上述定理中h(t)=et,且a,b满足1≤a,b≤ln 2+2c(a)-c(b),则P(v)=1-e-t,W(t)=e-t-e-2t-c(b)+2c(a),P、W均为增函数.

3. 可以类似地研究形如式(13)的多项和不等式.

设W(t)=P(2t+c(b)-2c(a))-P(t)是增函数. 如果x(t)满足

则

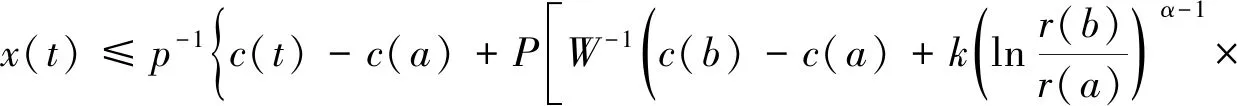
2.2 含有 Hadamard 分数阶积分的二元函数不等式

设i1=[u0,u1],i2=[v0,v1],其中u0≥0,v0≥0.假设

(ⅰ)x(u,v),f(u,v),c(u,v),gi(u,v),qi(u,v)∈C(i1×i2,+),i=1,2,…,k,k∈+,c(u,v)关于u、v均单调递增;

(ⅲ)hi(t)∈C(+,+)是增函数,且hi(t)≥1,i=1,2,…,k;

定理2.4假设当u∈i1,v∈i2时,

(20)

则

(21)

其中1<α,β<2,常数η定义为η=(lnu1-lnu0)α-1(lnv1-lnv0)β-1.

证明根据式(20)可知,当u∈[u0,u1],v∈[v0,v1],

x(u,v)≤(lnu-lnu0)(lnv-lnv0)c(u,v)+

(22)

定义

y(u,v)=(lnu-lnu0)2-α(lnv-lnv0)2-βc(u,v)+

其中u∈[u0,u1],v∈[v0,v1],则y(u,v)关于u,v均单调递增,且y(u0,v)=0.

由式(22)可得

(lnu-lnu0)1-α(lnv-lnv0)1-βx(u,v)≤y(u,v).

(23)

由假设(ⅲ)可知h(t)单调递增,故y(u,v)关于u求偏导可得

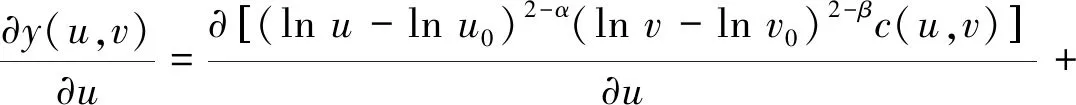
(24)

令η=(lnu1-lnu0)α-1(lnv1-lnv0)β-1, 式(24)变形为

(25)

令u=t,式(25) 两边对t从u0到u积分,由y(u0,v)=0得

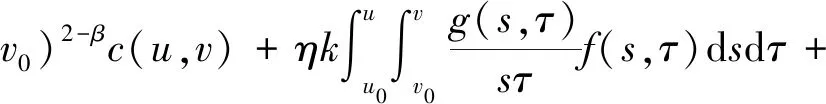
(26)

因为P是单调增函数,所以由式(23)和式(26) 可得式(21) 成立.

3 应 用

上述结论可用来研究相关分数阶积分方程解的性质.

例考虑下面分数阶积分方程连续解x(u,v)的有界性:

(27)

其中u∈[u0,u1],v∈[v0,v1],x(u,v),C(u,v),A(u,v),f(u,v),q(u,v)均为连续函数,1<α,β<2.

如果C(u,v)≤c(u,v)(lnu-lnu0)(lnv-lnv0),c(u,v)∈C([u0,u1]×[v0,v1],+),则上述方程的解x(u,v)满足

exp{[η(lnu-lnu0)2-α(lnv-lnv0)2-βc(u,v)+

(28)

η=(lnu1-lnu0)α-1(lnv1-lnv0)β-1.

证明由式(27)可得

|x(u,v)|≤c(u,v)(lnu-lnu0)(lnv-lnv0)+

令定理2.4中h(t)=t+1,t∈[a,b](a>0), 则有P(v)=ln(v+1),p-1(t)=exp (t)-1,且h(t)和P(v)均为增函数,η=(lnu1-lnu0)α-1(lnv1-lnv0)β-1.

根据定理2.4的结论即可得到方程(27)的解x(u,v)的估计式(28) .

4 结 论

本文建立了一个新的 Volterra-Fredholm 型分数阶积分不等式,推广了一些已知的不等式,比如

此外,它们还为求解分数阶常微分方程解的界提供了一种方便的工具. 本文不仅给出了关于单变量的Hadamard分数阶积分的Volterra-Fredholm型积分不等式,还给出了关于双变量的 Hadamard分数阶积分的积分不等式. 利用同样的方法可以研究关于广义比例 Hadamard 分数阶积分、Katugampola分数阶积分等对应的类似不等式.