正规三角矩阵余代数上的余导子

徐加成, 刘梦田, 王顶国, 鹿道伟

(①曲阜师范大学数学科学学院,273165,曲阜市;②淄博高新区统计中心,255035,淄博市;③济宁学院数学与计算机应用技术学院,273155,山东省曲阜市)

0 引 言

导子起源于分析理论,是代数学中一个非常重要的工具. 自20世纪50年代起,导子理论及其各种推广就被广泛研究并应用于构造各种代数系统[1-4]. 三角矩阵环是环和非交换代数经典理论中非常重要的结构和工具,其最著名的应用是Small巧妙地构造了一个右诺特但非左诺特的非交换环. 另外三角矩阵环在构造环论中的例子和反例时也被多次应用. 这其中用到的关键思想是双模能够阻断性质从一边转移到另一边. 具体可参考文献[5]、文献[6,p16-22] 和文献[7,p46-48,185,242,248,354-356]. 三角矩阵代数上的各种导子已被广泛研究[8-11].

1981年Doi Y[12]在研究余代数的上同调时引入了余导子,此概念在余代数理论中起着重要作用[13]. 2012 年Nakajima A[14]给出了余代数的广义余导子和内余导子的概念;2015年 Nakajima A[15]进一步做了推广,得到余环上三余导子的概念[16].

本文中,主要建立正规三角矩阵余代数的余导子与相关余代数和双余模上的余导子之间的关系.

论文安排如下:第1节回顾正规三角矩阵余代数和余导子的概念. 第2节给出正规三角矩阵余代数的余导子与相关余代数和双余模上余导子之间的关系.

本文中k是一个固定的域,chark≠2. 若无特别说明,所有的向量空间,张量积和态射均是k上的,⊗k简记为⊗. 应用 Sweedler符号表示余代数C的余乘法:Δ(c)=c1⊗c2,关于余代数和余模的更多内容考文献[17].

1 预备知识

设C、D为余代数,M为C-D-双余模,其中左、右余模结构分别为ρl:M→C⊗M和ρr:M→M⊗D.对任意m∈M,记

ρl(m)=m〈-1〉⊗m〈0〉,ρr(m)=m[0]⊗m[1].

令

回顾文献[18],T是一个余代数,余乘法和余单位如下,

任意的c∈C,d∈D,m∈M. 称T为正规三角矩阵余代数.

2 主要结果

本节将描述正规三角矩阵余代数T的余导子,并给出正规三角矩阵余代数的余导子与相关余代数和双余模上余导子之间的关系.

于是有

(1)

(2)

(3)

(4)

证明结论明显,证明从略.

则存在C的余导子δC和D的余导子δD,以及线性映射

ξ:M→C,τ:M→D,f:M→M,

满足:

(1)φ(c,m,d)=δC(c)+ξ(m),γ(c,m,d)=f(m),ψ(c,m,d)=δD(d)+τ(m).

(2)ξ是左C-余模同态,τ是右D-余模同态.

(3)ρl∘f=(δC⊗idM+idC⊗f)∘ρl,ρr∘f=(idM⊗δD+f⊗idD)∘ρr.

证明首先由δ是线性的可知

因此

φ(c,m,d)=φ(c,0,0)+φ(0,m,0)+φ(0,0,d),

γ(c,m,d)=γ(c,0,0)+γ(0,m,0)+γ(0,0,d),

ψ(c,m,d)=ψ(c,0,0)+ψ(0,m,0)+ψ(0,0,d).

对任意的c∈C,记δC(c)=φ(c,0,0),θ(c)=γ(c,0,0),ϑ(c)=ψ(c,0,0).因为δ是T的余导子,有

且

因此

δC(c1)⊗c2+c1⊗δC(c2)=ΔδC(c),

(5)

θ(c)〈-1〉⊗θ(c)〈0〉=c1⊗θ(c2),

(6)

θ(c)[0]⊗θ(c)[1]=0,

(7)

ϑ(c)1⊗ϑ(c)2=0.

(8)

于是θ=0,ϑ=0.

类似地,对任意的d∈D,记κ(d)=φ(0,0,d),υ(d)=γ(0,0,d),δD(d)=ψ(0,0,d). 可得δD是D的余导子,κ(d)=0,υ(d)=0.

另外有

φ(c,m,d)=δC(c)+φ(0,m,0),

(9)

γ(c,m,d)=γ(0,m,0),

(10)

ψ(c,m,d)=δD(d)+ψ(0,m,0).

(11)

最后对任意的m∈M,记ξ(m)=φ(0,m,0),f(m)=γ(0,m,0),τ(m)=ψ(0,m,0),有

且

因此

Δ(ξ(m))=m〈-1〉⊗ξ(m〈0〉),Δ(τ(m))=τ(m[0])⊗m[1],

f(m)〈-1〉⊗f(m)〈0〉=δC(m〈-1〉)⊗m〈0〉+m〈-1〉⊗f(m〈0〉),

f(m)[0]⊗f(m)[1]=m[0]⊗δD(m[1])+f(m[0])⊗m[1].

证毕.

对ξ和τ有如下关系.

命题2.3设δ如上定义. 对任意的m∈M,

(a)ξ(m)=εC(ξ(m〈0〉)m〈-1〉;

(b)τ(m)=εD(τ(m[0]))m[1];

(c)τ(m)+εC(ξ(m[0]))m[1]=0;

(d)ξ(m)+εD(τ(m〈0〉))m〈-1〉=0.

证明因为ξ是左C-余模同态,

ξ(m)=(idC⊗εC)Δξ(m)=(idC⊗εC)(idC⊗ξ)ρl(m)=εC(ξ(m〈0〉)m〈-1〉.

类似地有τ(m)=εD(τ(m[0]))m[1].一方面,由式(3),任意的c∈C,m∈M,

另一方面,因为δ是T的余导子,

可推出

τ(m)+εC(ξ(m[0]))m[1]=0.

类似计算可得(d). 证毕.

ξ:M→C,τ:M→D,f:M→M,

满足:

(a)ξ是左C-余模同态,τ是右D-余模同态;

(b)ρl∘f=(δC⊗idM+idC⊗f)∘ρl,ρr∘f=(idM⊗δD+f⊗idD)∘ρr;

(c)τ(m)+εC(ξ(m[0]))m[1]=0;

(d)ξ(m)+εD(τ(m〈0〉))m〈-1〉=0.

定义线性映射δ:T→T为

则δ是T的余导子.

证明一方面,

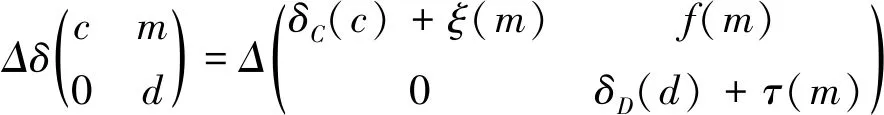
另一方面,

由条件(c)得

因为δC和δD分别为C和D的余导子,由条件(b)可得δ是T的余导子. 证毕.

根据命题2.2和命题2.4,得到下面主要结果.

其中δC和δD分别为C和D的余导子,且线性映射

ξ:M→C,τ:M→D,f:M→M,

满足:

(a)ξ是左C-余模同态,τ是右D-余模同态;

(b)ρl∘f=(δC⊗idM+idC⊗f)∘ρl,ρr∘f=(idM⊗δD+f⊗idD)∘ρr;

(c)τ(m)+εC(ξ(m[0]))m[1]=0;

(d)ξ(m)+εD(τ(m〈0〉))m〈-1〉=0.