覆冰导线振动数据降噪及状态识别∗

陶 慧，贺国帅，杨金显，艾朋伟

(河南理工大学电气工程与自动化学院，河南 焦作 454003)

由于自然条件的影响，输电线路会出现不同的运动形式，主要包括微风振动、次档距振动和覆冰舞动。其中覆冰舞动对输电线路的危害最大，低频大振幅的舞动会造成线路跳闸、金具磨损、停电、塔臂损坏等事故的发生，对输电线路覆冰舞动的识别及运动特征的提取可以为防舞装置设计提供依据[1－3]。李国倡通过监测输电导线舞动加速度信号，并进行姿态解算求舞动位移[4]。但导线的扭转使解算坐标系变化，解算的位移出现偏差。由三轴加速度计和三轴陀螺仪组成的微惯性测量组合(Micro Inertial Measurement Unit，MIMU)具有体积小、功耗低、抗振性能好和可靠性高等优点，已有学者将其用于输电线路运动监测[5－7]。黄新波等[8]设计基于MIMU 的导线舞动监测系统，解决了由于导线扭转使解算位移与实际位移存在偏差的问题。汪滔等[9]提出陀螺仪和加速度计进行互补滤波的改进算法，用于导线舞动轨迹还原。研究表明，使用MIMU 可以得到导线舞动位移，但陀螺漂移和加速度二次积分的累计误差，使得解算位移存在一定的偏差，要得到精确的位移，需要高精度的MIMU，成本昂贵。

因测量环境、传输路径和强噪声的干扰，采集的惯性数据中存在随机噪声，为精确识别覆冰导线运动状态，需对数据进行降噪处理。常用的振动信号降噪方法有小波阈值(Wavelet Threshold，WT)降噪[10]、经验模态分解[11](Empirical Mode Decomposition，EMD)和变分模态分解[12－13](Variational Mode Decomposition，VMD)。WT 降噪存在阈值、小波基函数和分解尺度等参数不能自适应选择的问题；EMD 存在分解时模态混叠和端点效应的问题；VMD有效克服了EMD 存在的问题，但参数不能自适应选择。唐贵基等[14]构建最小包络熵的适应度函数，利用粒子群算法优化VMD 参数组合，用于轴承故障诊断；陈鹏等[15]构建L－峭度与相关系数的自适应度函数，利用鱼群算法优化VMD 参数，实现振动信号的自适分解降噪。建立合理的目标函数，选择搜索能力强的优化算法，可实现VMD 参数的自适应选择。麻雀搜索算法(Sparrow Search Algorithm，SSA)是薛建凯等[16]受麻雀的觅食行为和反捕食行为的启发，提出的一种新型优化算法。SSA 具有全局搜索能力强、收敛速度快等优点，被广泛使用[17－18]。

输电导线运动状态变化会导致导线运动能量的变化，能量可以作为输电导线运动特征。MIMU 采集的不同运动状态的导线各维能量分布不同，KL 散度(Kullback Leibler Divergence)用来衡量两个分布之间的差异，李一鸣基于EEMD-KPCA 提取垮落煤岩的特征向量，利用KL 散度实现垮落煤岩的识别[19]。本文将不通过姿态解算，直接从振动信号能量分布入手，进行覆冰导线状态识别。使用SSA 优化VMD 参数，利用优化后的VMD 将真实振动信号与噪声分离，选取真实振动信号重构，完成振动信号降噪预处理。对降噪后的6 维信号计算能量分布，提出E-KL(Energy-Kullback Leibler Divergence)散度法，对覆冰导线的状态进行识别及幅频估计。

1 SSA-VMD 降噪算法

1.1 麻雀搜索算法(SSA)简介

SSA 将初始种群分为发现者和加入者，发现者负责为整个种群提供觅食区域和方向，加入者利用发现者来获取食物，当麻雀种群意识到危险时，警惕着会做出反捕食行为，警惕者的数量占种群的10%～20%，它们的初始位置在种群中随机产生[16]。SSA 的更新方式主要为发现者、加入者和警惕者的位置更新。

发现者的位置更新如下:

式中:t为当前迭代次数；itermax为最大迭代次数；Xi，j为第i个麻雀在第j维的位置信息；α为随机数，α∈[0，1]；R2为预警值，R2∈[0，1]；ST 为安全值，ST∈[0.5，1]；D为服从正态分布的随机数；L为1×d的矩阵，其中该矩阵内每个元素全部为1。

加入者的位置更新如下:

式中:Xp是目前发现者所占据的最优位置，Xworst则表示当前全局最差的位置。A表示一个1×d的矩阵，其中每个元素随机赋值为1 或－1，并且A＋＝AT(AAT)－1。

警惕者的位置更新如下:

式中:Xbest为当前的全局最优位置；β为步长且服从标准正态分布；C代表一个随机数，C∈[－1，1]；fi为当前麻雀个体的适应度值；fg为当前全局最佳适应度；fw为当前全局最差的适应度值；ε为常数，以避免分母出现0。

1.2 变分模态分解(VMD)原理

VMD 是一种完全非递归、自适应的信号处理方法，通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽，从而能够自适应地实现振动信号频域的有效分离[12]。VMD 把振动信号分解为K个本征模态函数(Intrinsic Mode Function，IMF)。每一个IMF 均被视为调幅－调频的信号uk(t):

式中:Ak(t)为幅值；φk(t)为相位。

具体分解步骤如下:

①对每一个模态分量信号uk(t)，利用Hilbert变换计算与之对应的解析信号，得到单边频[δ(t)＋j/πt]×uk(t)，其中δ(t)为脉冲函数。

②加入指数项e－jωkt，将每个模态的频谱转移至基带{[δ(t)＋j/πt]×uk(t)}e－jωkt，其中ωk为模态分量信号的中心频率。

③得到受约束的变分问题:

④引入二次惩罚因子α和拉格朗日乘子λ(t)构造扩展拉格朗日表达式Γ(uk，ωk，λ):

通过反复迭代，寻找扩展拉格朗日表达式的鞍点求解最小值，获得最优解。最优解为本征模态函数{uk}及各自的中心频率{ωk}。

VMD 分解层数K过小导致信号欠分解，K过大导致信号过分解；二次惩罚因子α过小，IMF 出现额外“噪声”信息，过大会丢失部分信息，合适的K和α是保证真实振动信号与噪声分离的前提。

1.3 适应度函数的选取

振动信号经VMD 分解为一系列IMF 后，通过相关系数、排列熵和包络熵结合区分真实振动信号和噪声。

相关系数[15]表示IMF 与原始信号之间的相关程度，IMF 与原始信号的相关系数越小，即含噪声越多；反之，包含真实振动信号越多。IMF 与原始信号之间的相关系数ri为:

式中:xi为IMF；为IMF 均值；y为原始信号；为原始信号均值；i＝1，2…K。

排列熵是一种检测动力学突变和时间序列随机性的方法，其大小表示时间序列的随机程度。熵值越小，时间序列越简单、规则；熵值越大，时间序列越复杂、随机。参考文献[20]，第i个IMF 的排列熵HPE(i)表达式为:

式中:Pj为IMF 相空间重构后第j种符号序列出现的概率大小。

包络熵表示振动信号的稀疏程度，输电线路振动呈周期性，由于随机噪声的干扰，使振动信号周期性降低，信号稀疏性较弱，熵值较大。参考文献[14]，第i个IMF 的包络熵Ep(i)表达式为:

式中:Qj是a(j)的归一化形式，a(j)是IMF 经Hilbert 解调后得到的包络信号。

相关系数保证信号不失真，排列熵保证信号的有序、规则，包络熵保证信号的周期性。构建相关系数的倒数、排列熵和包络熵三者叠加的适应度函数，能很好地将真实振动信号和噪声分离。适应度函数定义如下:

1.4 SSA-VMD 降噪算法具体步骤

SSA 算法的种群搜索空间为VMD 待优化的参数K、α的范围，Xi＝[Ki，αi]为麻雀i的位置。

算法具体步骤如下:

①参考文献[21]定义SSA 初始参数。最大迭代次数为10，麻雀种群数量为40，发现者比例为20%，警惕者比例为20%，安全值为0.7，设置K∈[2，10]，α∈[100，2 000]。

②初始化麻雀的位置。随机生成若干参数组合[K，α]作为麻雀种群的初始位置，计算每只麻雀的适应度值，获取初始种群中最优适应度fbest和最优位置Xbest。

③更新种群中的发现者、加入者和警惕者的位置。并计算其适应度值，更新最优适应度值和最优位置。

④满足最大迭代次数，停止迭代，输出最优参数组合，不满足转至步骤3。

⑤利用SSA 寻找到的最优参数组合对原始振动信号进行VMD 分解，得到一系列IMF 分量。

⑥选择合适的IMF 分量进行信号重构。

算法流程如图1 所示。

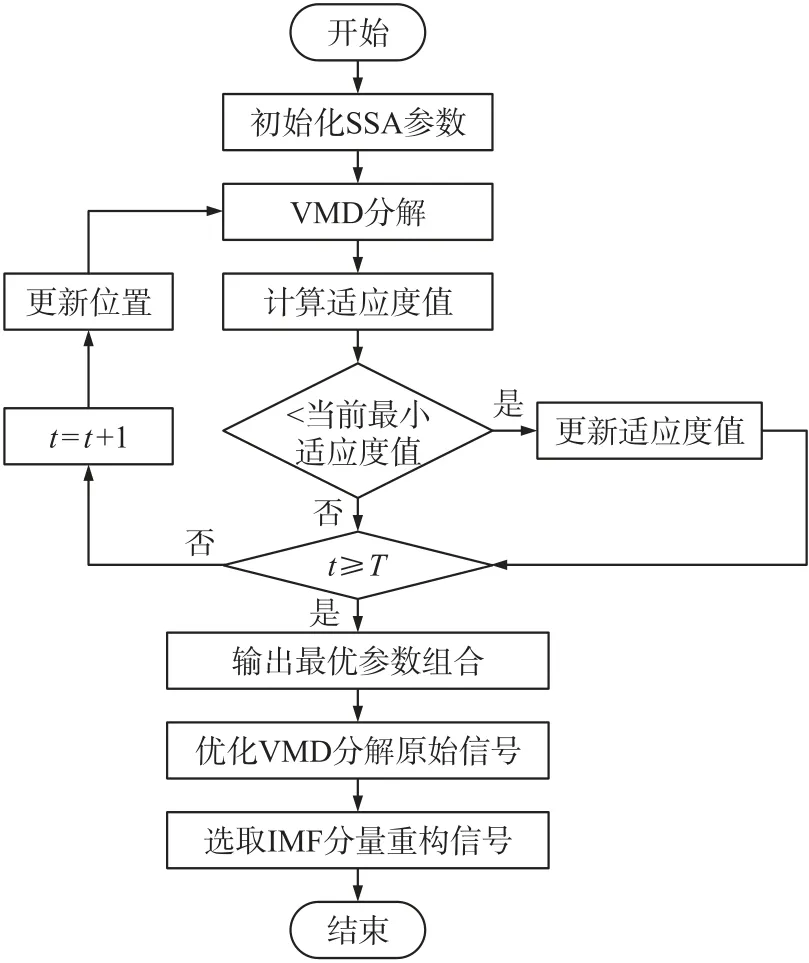
图1 降噪算法流程图

1.5 仿真信号降噪

1.5.1 仿真信号构建

输电线路做类似正弦的周期性振动，运动形式包括高频微幅的微风振动(频率为3 Hz～150 Hz，最大振幅不大于导线直径的2～3 倍)、中频中幅的次档距振动(频率范围在1 Hz～2 Hz，振幅在0.1 m～0.5 m)和低频大振幅的舞动(频率在0.1 Hz～3 Hz，振幅最高可达几十米)[22]。构造式(11)的仿真信号，模拟输电线路不同运动状态，验证降噪方法用于输电导线振动信号的可行性。z1(t)模拟覆冰舞动，z2(t)模拟次档距振动，z3(t)模拟微风振动，ηi(t)为[－2，2]的随机噪声。仿真信号采样频率为300 Hz，采样时间为10 s。

1.5.2 适应度函数选取的合理性

以z1(t) 为例，用信噪比(SNR)、均方误差(RMSE)、峰值信噪比(PSNR)和噪声抑制比(NNR)作为降噪效果评价标准[23－24]，验证适应度函数选取的合理性。采用SSA-VMD 降噪算法，选取不同适应度函数对z1(t)进行处理，得到的降噪结果如表1所示。

表1 不同适应度函数降噪效果对比

由表1 可以看出:以排列熵、包络熵和相关系数的倒数结合作为适应度函数时，仿真信号的SNR、PSNR 和NNR 最大，RMSE 最小，此时信号降噪效果最好。

1.5.3 不同优化算法过程对比

用式(10)构建的适应度函数，分别采用遗传算法和粒子群算法优化VMD 参数对z1(t)进行处理，和SSA 的优化过程比较，如图2 所示。

图2 不同算法优化过程

由图2 可以看出:SSA 寻找到的适应度值最小，且迭代次数最少，优于粒子群算法和遗传算法。

1.5.4 仿真信号处理

采用SSA-VMD 降噪方法对z1(t)、z2(t)和z3(t)进行处理，SSA 优化VMD 结果及式(10)计算的IMF适应度值如表2 所示。根据表2:z1(t)中IMF1 适应度值最小，且与其余IMF 分量相差较大，IMF1 为真实振动信号，其余IMF 为噪声分量，z1(t)选择IMF1重构信号；同样，z2(t)选择IMF1 重构信号；z3(t)中IMF8 和IMF9 适应度值较小，为真实振动信号，其余IMF 为噪声分量，z3(t)选择IMF8 和IMF9 重构信号。同时对比WT 降噪、EMD 降噪和VMD(固定VMD 参数为[4，2 000])降噪，四种降噪方法结果如表3 所示。

表2 SSA 优化VMD 结果及IMF 适应度值

表3 不同降噪方法结果对比

由表3 可以看出:使用SSA-VMD 方法降噪处理后，仿真信号的SNR、PSNR 和NNR 最大，RMSE 最小，降噪效果明显优于WT 降噪、EMD 降噪；相对于固定参数的VMD 降噪算法，降噪效果也有一定程度的改善。

1.6 实测信号降噪

设计输电线路覆冰实验，将MIMU 安装在覆冰导线悬挂点处，如图3 所示。采样频率为300 Hz，采样时间为20 s，采集覆冰舞动三轴加速度和三轴角速度数据，对数据进行降噪处理，覆冰舞动数据降噪结果如图4 所示。由图4 可以看出:覆冰舞动原始三轴加速度和三轴角速度数据经降噪处理后，滤除了随机噪声造成的异常数据点，没有尖峰毛刺等现象，降噪后振动信号波形更加平滑，周期性更加明显。

图3 覆冰导线测试系统

图4 覆冰舞动原始数据及降噪结果

对覆冰舞动数据使用WT 降噪、EMD 降噪、VMD(固定VMD 参数为[4，2000])降噪和SSAVMD 降噪方法处理。由于实际测试中无法得到不含噪声的真实振动信号，无法利用SNR、RMSE 和PSNR 评价降噪效果，这里只利用NNR 来评估实际测量数据的降噪效果[23－24]。以NNR 为评价标准，4种降噪方法噪声抑制结果如表4 所示。

表4 覆冰舞动NNR 对比

由表4 可以看出:SSA-VMD 降噪方法NNR 最大，噪声抑制效果最好。次档距振动和微风振动数据使用同样的方法处理，也能得到较好的效果，这里不再给出。

2 基于E-KL 散度的覆冰导线运动状态识别

物体运动状态的改变，会导致其能量变化，同理输电导线运动状态变化会改变导线运动幅值和运动频率，进而导致导线运动能量分布的变化。将降噪后数据6 维能量分布与KL 散度结合提出E-KL 散度，对覆冰导线运动状态进行识别。

2.1 E-KL 散度计算

采集输电导线三轴加速度和三轴角速度数据，降噪后表示为:

式中:ax，ay，az为降噪后三轴加速度，ωx，ωy，ωz为降噪后三轴角速度；记为X＝{x1，x2，…xi，…，x6}，xi＝{ai1，ai2，…，aij，…，aiN}T，N为序列长度。则xi的能量为:

对不同运动状态导线6 维能量分布SⅠ、SⅡ，使用E-KL 散度来度量这两个能量分布之间的相似程度[19]，E-KL 散度定义如下:

E-KL 散度值越小，则SⅠ与SⅡ的能量分布越接近，即运动状态越相似。

2.2 覆冰导线运动识别

相同运动状态的输电导线能量分布相似，即E-KL散度值较小，计算不同运动状态导线之间的E-KL散度值进行比较，对输电导线运动状态进行识别。

实验采集10 组覆冰舞动数据、10 组微风振动数据和10 组次档距振动数据，新采集一组“未知状态”导线运动数据。不对原始数据进行降噪处理，根据式(13)、式(14)计算不同运动状态导线6 维能量分布，根据式(15)计算新采集“未知状态”数据和已采集的数据(共30 组)之间的E-KL 散度值，结果如图5 所示。

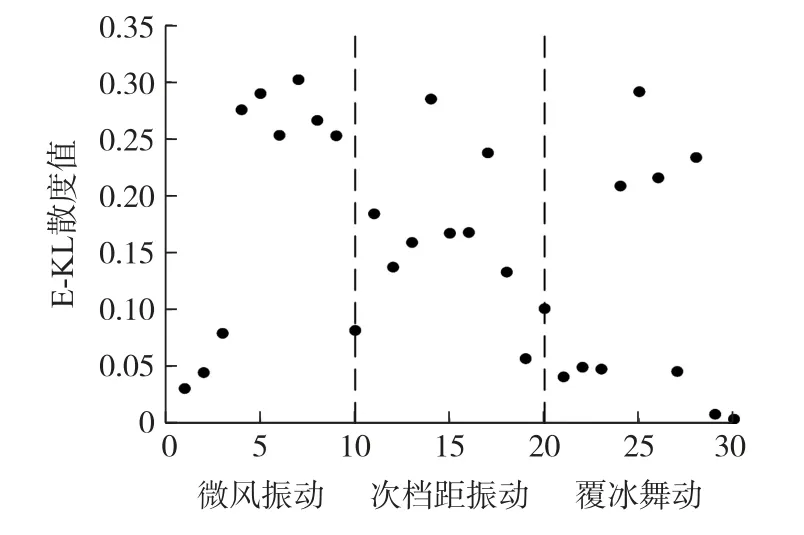
图5 原始数据E-KL 散度值

由图5 可以看出:数据不降噪时，“未知状态”导线运动状态难以识别。

对30 组已采集数据及“未知状态”数据采用SSA-VMD 方法降噪处理，降噪后数据E-KL 散度值如图6 所示。

图6 降噪后数据E-KL 散度值

由图6 可以看出:经过降噪处理后，新采集的“未知状态”数据与10 组微风振动数据的E-KL 散度值最大，与10 组次档距振动数据的E-KL 散度值次之，与覆冰舞动数据之间的E-KL 散度值最小。说明“未知状态”数据运动状态与覆冰舞动运动状态最相似，可以判定“未知状态”为覆冰舞动。次档距振动与微风振动识别方法与覆冰舞动类似，不再给出。

2.3 覆冰导线运动状态估计

导线运动状态改变使导线运动幅值及运动频率变化[25]。计算不同运动状态输电导线相同时间段数据之间的E-KL 散度值，度量导线运动幅值变异程度，不同运动状态导线之间的E-KL 散度值越小，说明运动状态越相似，即导线幅值变异程度越低。对于同种运动状态的输电导线，导线运动信号的变化频率就是导线运动频率，计算当前时间段与上一时间段数据之间的E-KL 散度值，度量导线运动频率变异程度，E-KL 散度值越小，说明当前时间段导线运动状态与上一时间段导线运动状态越相似，即导线运动频率变异速率越慢。

将输电导线静止时采集的数据作为初始状态。采集三种导线运动数据和初始状态数据并分段处理，每段采样点数为150，共分50 组。计算三种导线运动数据与初始状态在同一时间段的E-KL 散度值，度量导线运动幅值变异程度，三种导线运动幅值变异程度如图7 所示。

图7 三种运动形式幅值变异对比图

由图7 可以看出:覆冰运动为大振幅舞动，次档距振动为中幅运动，微风振动为低幅运动。

分别计算三种导线运动状态当前时间段与上一时间段之间的E-KL 散度值，估计导线运动频率变异程度，结果如图8(a)所示，为更直观对比频率变异程度，图8(a)纵轴范围0～0.1 如图8(b)所示。

图8 三种运动形式频率变异对比图

由图8 可以看出:微风振动为高频运动，次档距振动为中频运动，覆冰运动为低频舞动。

3 结论

利用MIMU 采集输电导线振动原始数据，不经过姿态解算，从原始数据出发，提出基于SSA-VMD和E-KL 散度的覆冰导线振动数据降噪及状态识别方法。利用构建的适应度函数，使用SSA 优化VMD参数将真实振动信号与噪声分离，选取真实振动信号重构完成降噪，仿真信号和实测信号表明降噪方法能有效实现对覆冰导线数据降噪。提出的SSAVMD 降噪方法可为其他振动信号的降噪提供参考。计算导线各维能量，构建E-KL 散度对覆冰导线状态识别，估计覆冰导线幅值和频率变异程度。基于E-KL 散度能有效识别覆冰导线状态并进行幅频估计，可为防舞装置的设计提供了依据。