一类2+1维群体平衡方程的尺度变换群分析及自相似解
2024-01-26林府标张千宏
林府标,王 骞,张千宏
(1.贵州财经大学 数学与统计学院,贵州 贵阳 550025;2.贵州师范大学附属中学,贵州 贵阳 550001)
0 引言
群体平衡方程[1-4]广泛用于固体物的破损过程、细胞种群的生长过程、聚合过程、 结晶和沉淀过程、基因调控过程、分散相系统、环境和工程学、农业工程学、生物医学工程学、血液学、制药工程学、生物化学、分子生物学、形态结晶学、细胞生物学等.
群体平衡模型在实体应用领域,关键是缺乏精确求解的技术和理论,而偏微分方程目前已提出多种解析研究途径[5-6],因此,研究方法常采用数值离散方案,如矩方法、蒙特卡罗方法等[1-4].既有聚合又有破损过程的群体平衡方程[1-2]可写成

(1)
式中:x为微粒的尺寸坐标;t为时间;f(x,t)刻画t时刻种群密度分布;v(x,t)描述尺寸为x的微粒在t时刻破损的平均数量;b(x,t)刻画微粒在t时刻破损的频率,代表单位时间内正在破损的部分;p(x|y)刻画尺寸为y、破损尺寸为x的微粒的粒度分布,满足

其值由实验观测或破损过程的实体模型决定.聚合核K(x,y)刻画尺寸为x和y的微粒对聚合的频率,满足
K(x,y)=K(y,x)≥0.
γ次齐次核[1-2]
K(λx,λy)=λγK(x,y),
(2)
广泛应用于实体科学工程领域,其中,γ,λ均为常数,γ是齐次的度.如数学上易处理的齐次核[1-4]为
(3)
式中,ki(i=0,…,4)为正常数.选取v(x,t)、p(x|y)和b(x,t)分别为
(4)
式中,ν,κ,p均为常数,κ>0,p≥0.若令y=xs,用式(2)可得
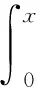
(5)
因此,用式(4)和式(5),方程(1)可写成

(6)
方程(6)的解析解法和精确解既重要又缺乏,经典李群方法[7-9]不能用于研究方程(6),需用改进的李群理论[10-11],但此方法最大困难和障碍是求解决定方程[12-14].受前人的工作[10-11]和文献[12-14]的启发,该文用尺度变换群方法研究方程(6)的群不变量、自相似解、精确解、约化方程.
1 尺度变换群
假设方程(6)接受的尺度变换群为
(7)
其中,a,λ1,λ2,μ均为常数,式(7)对应的无穷小李对称算子为
(8)
依据式(7)的假设,变换群式(7)将方程(6)的任一解f=f(x,t)变成同一方程
(9)
的解.因此,将式(7)代入方程(9),由式(2),得到
(10)
注意f=f(x,t)是方程(6)的任一解,由方程(10)推出
λ2=-λ1p,μ=(p-γ-1)λ1.
(11)
类似于式(7),可以验证方程(6)接受平移变换群
(12)

定理1方程(6)的不变群的部分生成元,构成一个2维的子李代数L2=span{X1,X2},并有下列一组基
(13)
定理2设用改进的李群分析法,获得方程(6)的不变群的全体生成元,构成的李代数为L,则有L2⊆L.
2 自相似解
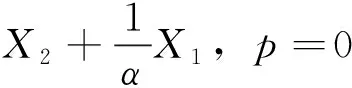
2.1 情形K(x,y)=k0
针对K(x,y)=k0,用式(2),得到γ=0.算子X1,p≥0对应的群不变量为J1=x,J2=f.因此,方程(6)的解可以写成
f(x,t)=φ(x),
其中,φ(x)满足约化方程
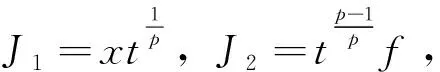
其中,φ(z)满足约化方程
可以验证
是方程(14)的解.因此,方程(6)的精确解为
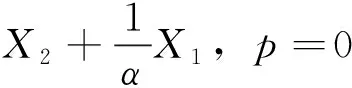
f(x,t)=exp(-α(t+τ0))φ(z),z=xexp(-α(t+τ0)),
其中,φ(z)满足约化方程
(15)
可以验证
是方程(15)的解.因此,方程(6)的精确解为
2.2 情形K(x,y)=k1(x+y)
针对K(x,y)=k1(x+y),用式(2),得γ=1.算子X1,p≥0对应的群不变量为J1=x,J2=f.因此,方程(6)的解可以写成
f(x,t)=φ(x),
其中,φ(x)满足约化方程
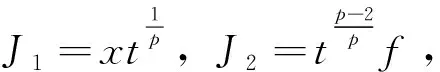
其中φ(z)满足约化方程
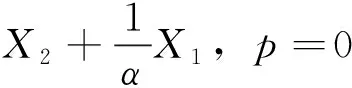
f(x,t)=exp(-2α(t+τ0))φ(z),z=xexp(-α(t+τ0)),
其中φ(z)满足约化方程
2.3 情形K(x,y)=k2xy
针对K(x,y)=k2xy,由式(2),可知γ=2.算子X1,p≥0对应的群不变量为J1=x,J2=f.因此,方程(6)的解可以写成
f(x,t)=φ(x),
其中,φ(x)满足约化方程
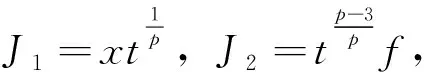
其中,φ(z)满足约化方程

(16)
可以验证
是方程(16)的解.因此,方程(6)的精确解为
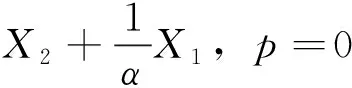
f(x,t)=exp(-3α(t+τ0))φ(z),z=xexp(-α(t+τ0)),
其中,φ(z)满足约化方程
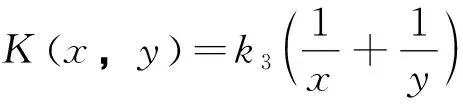
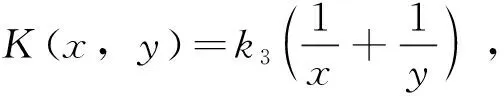
f(x,t)=φ(x),
其中,φ(x)满足约化方程

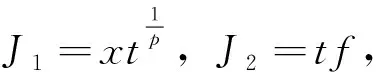
其中,φ(z)满足约化方程

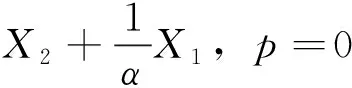
f(x,t)=φ(z),z=xexp(-α(t+τ0)),
其中,φ(z)满足约化方程


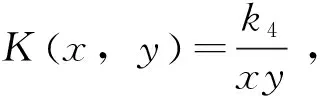
f(x,t)=φ(x),
其中,φ(x)满足约化方程
其中,φ(z)满足约化方程

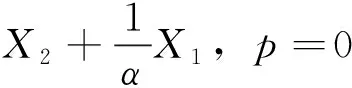
f(x,t)=exp(α(t+τ0))φ(z),z=xexp(-α(t+τ0)),
其中,φ(z)满足约化方程

3 结论
尺度变换群方法不但可以用于方程(6),而且获得了自相似解、精确解及约化方程.用此方法研究一个新的群体平衡方程,不需要很棘手地求解决定方程.若L=L2成立,则本文所有结果均为完全的,否则仅为非完全的.能否直接用改进的李群技术[11-14]研究方程(6)的全体生成元,判断L=L2正确与否,值得在今后的研究中思考.
