施工升降机吊笼结构动态特性仿真分析与拓扑优化

涂 宇，王 怡，罗建阳，胡自化，杨 丽，汤妙妙

(1.湖南交通工程学院，湖南 衡阳 421001；2.中南大学 土木工程学院，湖南 长沙 410075；3.湘潭大学 机械工程与力学学院，湖南 湘潭 411105)

0 引言

施工升降机作为施工现场常见机械，承担了运输物资的重要任务.通过施工升降机可以快速地将物料从底层运送到高层，极大地提升了高层建筑的施工效率.施工升降机主要由吊笼、导轨架、附墙架、安全装置和驱动机构组成.吊笼承载物料，其顶部常放有电机，其传动系统由齿轮齿条啮合组成.因此，吊笼容易受到电机和冲击载荷的影响，引发结构共振；其危害轻则导致吊笼本身的振动，重则导致吊笼结构的损坏[1-3]，因此，文中对吊笼进行模态分析，研究其与外界激振频率发生共振的可能性，并对其结构采用拓扑优化方法进一步改进，然后将优化前后的模态分析进行对比，分析优化吊笼结构的安全性，并对其进行谐响应分析，计算其共振频率区间.

模态分析通过研究模型的模态参数，可以得到模型在机械振动方面的数据，从而为模型的优化提供指导价值[4].邹伟东等[5]以大型升降平台的车架为研究对象，建立了车架的动力模型并对其进行了模态分析，得到了共振产生时的最大损伤位置，为车架添加加强筋提供了依据.陆崇义[6]以传动齿轮为例将模态分析应用到机械的故障诊断中，通过对比正常和故障齿轮的模态分析结果的差异，验证了将模态分析应用到机械故障诊断中的可行性.李飞伟[7]利用ANSYS对机械臂进行模态分析，校核了机械臂在不稳定工况下的强度，得到了前10阶的模态振型结果，对机械臂的设计制造有一定的参考价值.郑彬等[8]对发动机的连杆结构进行有限元模态分析以防止连杆的振动破坏，根据模态分析的结果分析出连杆大头与杆身之间的过渡区域是最容易发生振动破坏的位置，为发动机连杆设计提供了参考.

1 吊笼模态分析

吊笼是施工升降机运输人员和物料的笼形部件，施工时吊笼沿着导轨架垂直升降，将物料或人员从底层运送到高层.主要由吊笼门(双开门、单开门)、吊笼门配重、限速器安装板、滚轮、围板、围栏等组成.

利用SOLIDWORKS对SC200型吊笼进行建模，对吊笼进行一些简化，省略了吊笼门、吊笼内板、吊笼门对重等不影响吊笼结构强度的附件，只保留吊笼的主要框架、受力梁等.吊笼三维模型如图1所示.

图1 SC200型吊笼三维模型图Fig.1 SC200 type cage 3D model

1.1 吊笼模态分析流程

利用ANSYS对吊笼进行模态分析[9-12].首先将吊笼模型转换为“x_t”格式，导入到ANSYS中，选择模态分析；设置材料为Q345，材料密度为7 850 kg/m3，弹性模量为210 MPa，泊松比为0.3.在Design Modeler中设置吊笼整体为一个“部件”，删除吊笼中多余的接触，划分吊笼的网格，设置吊笼结构的网格划分方法为四面体划分，划分出的网格如图2所示，共有183 976个节点，由89 456个单元组成.

图2 SC200型吊笼网格划分模型Fig.2 SC200 type cage meshing model

在吊笼后方的两个槽钢位置定义固定支撑，选择模态分析的阶数为6阶，输出结果为总变形，然后进行仿真计算，得出的吊笼的固有频率如表1所示.1阶～6阶的模态振型如图3所示.

表1 吊笼模态分析的前6阶固有频率表

图3 吊笼的模态振型图：(a)1阶；(b)2阶；(c)3阶；(d)4阶；(e)5阶；(f)6阶Fig.3 Modal vibration diagram of the cage：(a)1nd；(b)2nd；(c)3nd；(d)4nd；(e)5nd；(f)6nd

图3(a)中，频率为7.68 Hz时，吊笼右侧和中部有向后突出扭曲的倾向，最大变形位于吊笼前方上部左右两侧支架处，1阶模态的最大变形量为2.92 mm.图3(b)中，频率为9.67 Hz时，吊笼左侧区域有向前方扭曲的倾向，吊笼右侧区域有向后方扭曲的倾向，最大变形位于吊笼前方下部左右框架的两个角处，2阶模态的最大变形量为3.73 mm.图3(c)中，频率为15.11 Hz时，吊笼有向前方倾斜的倾向，最大变形位于吊笼最前方的整个框架处，3阶模态的最大变形量为2.73 mm.图3(d)中，频率为19.04 Hz时，吊笼左右两侧中间与钢板连接区域有向后方凸出的倾向，最大变形区域位于吊笼前方右边支架的中间，4阶模态的最大变形量为10.74 mm.图3(e)中，频率为20.24 Hz时，吊笼的前方左侧中间位置有后方凸出的倾向，前方右侧中间位置有前方凸出的倾向，最大变形区域位于吊笼前方左右两边的钢板与支架连接处，5阶模态的最大变形量为11.33 mm.图3(f)中，频率为20.76 Hz时，吊笼的前方左右两侧中间位置有向前方凸出的倾向，后方左右两侧中间位置有向后方凸出的倾向，最大变形区域位于吊笼后方左侧支架的中间，6阶模态的最大变形量为12.61 mm.

1.2 施工升降机激振频率

本施工升降机在施工时产生的激振频率有电机驱动的转动频率与齿轮齿条的啮合频率.施工升降机电机采用三相异步电机，其磁极对数通常为2、4、6、8、10等偶数，根据电机转速公式，如下所示：

n=f/p.

(1)

式中：n为电机转速的数值，单位r/s；f为电源频率的数值，单位Hz；p为磁极对数.因此，其转动频率为525 Hz.

齿轮齿条在施工过程中相互啮合，其啮合频率[13-14]的计算公式分别如下所示：

fm=Z·n，

(2)

式中：fm为啮合频率的数值，单位Hz；Z=8为齿轮齿数；n为齿轮转速的数值，单位r/s.在施工时吊笼正常的运行速度区间为20～60 m/min，因此，齿轮的啮合频率范围为13.26～39.79 Hz.

1.3 结果分析

施工升降机的激振频率为13.26～39.79 Hz，而吊笼的模态频率为7.68～20.76 Hz.其中，吊笼4阶、5阶和6阶模态频率结果与激振频率存在重叠，因此，考虑使用拓扑优化的方法对吊笼的结构进行一些改进，尝试降低吊笼的最大频率和变形量.

2 吊笼拓扑优化

由于吊笼模态频率与施工升降机激振频率存在较大的重叠，因此，本节将采用拓扑优化的方法对其结构进行优化设计，通过降低其固有频率，尽量减少共振现象的发生.

2.1 吊笼优化模型建立

吊笼模态拓扑优化是在模态分析基础上进行的优化.优化模型和上一节的模态分析模型不同，上一节吊笼只留下了基础框架，这些基础框架是主要的受力部件，不能对其进行优化，所以需要保留可优化的区域.因此，在吊笼的前后面增加4个连接面，在前方两个连接面中间留出放置驾驶室的空间，对连接面进行优化，根据优化的结果实现对实际模型的改进优化.吊笼拓扑优化前的模型如图4所示.

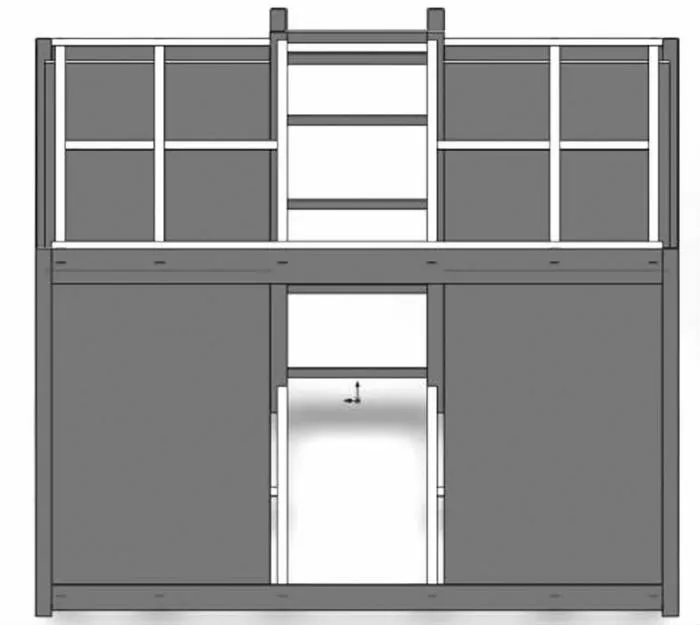
图4 吊笼拓扑优化前的模型Fig.4 Model before cage topology optimization

2.2 吊笼拓扑优化流程

利用ANSYS对吊笼进行模态分析拓扑优化.设置材料为Q345，材料密度为7.85 g/cm3，弹性模量为210 MPa，泊松比为0.3.设置吊笼整体为一个“部件”，删除吊笼中多余的接触，划分吊笼的网格，节点数量为136 256，单元数量为66 043.在后方槽钢处设置固定约束，设置优化区域为前后4个连接面，目标函数为吊笼的六阶模态频率最小化，设置响应约束为质量保留30%和65%.然后进行求解计算，根据软件迭代计算，质量保留30%和65%的拓扑优化结果如图5所示.

图5 吊笼拓扑优化的结果：(a)质量保留30%；(b)质量保留65%Fig.5 Results of cage topology optimization：(a)Weight retention 30%；(b)Weight retention 65%

图5(a)中，在前后连接面体积保留30%时，吊笼前方区域基本没有保留，只有4个角落和面中间的一小块区域得到了保留；吊笼的后方区域优化的部分主要集中在左右两侧中间部件，在靠近槽钢处的两块区域保留了下来，中间的小部分凸出的区域，上下部分各有一大部分没有优化.图5(b)中，在前后连接面体积保留65%时，吊笼前方区域中间部分被优化去除了；吊笼的后方大部分区域都得到了保留，只有两侧中间的一大块区域被优化去除了.综合两个优化结果图像来看，吊笼前方连接面基本都需要优化，而后方连接面两侧的部分需要优化.

2.3 吊笼优化模型

根据吊笼拓扑优化结果对吊笼框架进行设计优化，根据实际的模型和拓扑优化结果进行综合考虑，尽量在节省材料和焊接方便等前提下完成吊笼的进一步优化设计.具体优化方案如下，前方区域的框架变化小，后方的方管由竖直放置改为使用两个方管倾斜放置，中间设置角钢连接以固定结构，优化后吊笼模型如图6所示.

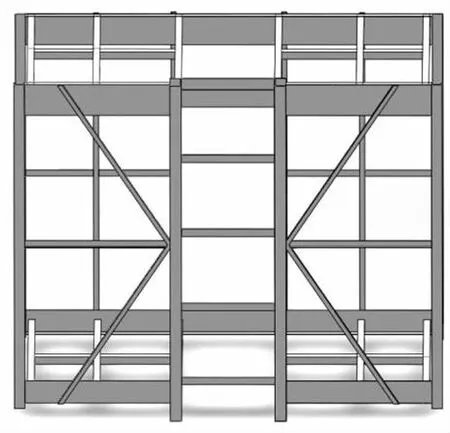
图6 吊笼优化后的三维模型Fig.6 Optimized 3D model of the cage

3 优化后吊笼模态分析

为了验证优化后吊笼的模态参数变化，需要对优化后的吊笼进行模态分析.将优化后的吊笼模型导入ANSYS中，定义的材料属性和约束条件同上节；使用四面体网格，定义为30 mm，整体模型网格的节点数量为220 008，单元数量为104 630.计算得出的优化后吊笼模态分析的前6阶固有频率如表2所示.1阶～6阶的模态振型如图7所示.

表2 优化后吊笼模态分析的前6阶固有频率表

图7 优化后吊笼的模态振型图：(a)1阶；(b)2阶；(c)3阶；(d)4阶；(e)5阶；(f)6阶Fig.7 Modal vibration diagram of the optimized cage：(a)1nd；(b)2nd；(c)3nd；(d)4nd；(e)5nd；(f)6nd

图7(a)中，在1阶模态时，吊笼由前方向后方扭曲，表明在频率为6.1 Hz时，吊笼中部和右侧有向后扭曲突出的倾向，最大变形区域出现在吊笼前方上部左右两侧支架处，1阶模态时的最大变形量为2.88 mm.图7(b)中，在2阶模态时，吊笼向前后倾斜，而且比1阶模态时变形还要大，表明在频率为7.87 Hz时，吊笼左侧有向前方扭曲的倾向，右侧有向后方扭曲的倾向，最大变形区域出现在吊笼前方下部左右框架的两个角处，2阶模态时的最大变形量为3.67 mm.图7(c)中，吊笼在3阶模态时向前方倾斜，表明在频率为13.63 Hz时，吊笼整体有向前倾斜的倾向，最大变形区域出现在吊笼最前方的整个框架处，3阶模态时的最大变形量为2.75 mm.图7(d)中，在4阶模态时，吊笼左右两侧中间位置向后方凸出，其他位置没有太大的变形，表明在频率为17.23 Hz时，吊笼左右两侧中间位置有向后方凸出的倾向，最大变形位于吊笼前方左右边支架中间，4阶模态时的最大变形量为10.45 mm.图7(e)中，在5阶模态时，吊笼前方左侧中间位置向后方凸出，右侧中间位置向前方凸出，其他地方没有太大的变形，表明在频率为18.07 Hz时，吊笼的前方左侧中间位置有后方凸出的倾向，前方右侧中间位置有前方凸出的倾向，最大变形区域出现在吊笼前方右边支架中间，5阶模态时的最大变形量为11.35 mm.图7(f)中，在6阶模态时，振型前方左右两侧中间位置向前方凸出，后方左右两侧中间位置向后方凸出，表明在频率为18.88 Hz时，吊笼的前方左右两侧中间位置有向前方凸出的倾向，吊笼的后方左右两侧中间区域有向后方凸出的倾向，最大变形位于吊笼后方左侧支架中间，6阶模态时的最大变形量为9.58 mm.

4 结论

根据吊笼优化前后的模态分析结果可以得出，吊笼的六阶模态固有频率在优化后都有一定的降低，降低了1～2 Hz，而且在前5阶振型最大变形量比较接近的情况下，第6阶模态振型的最大变形量降低了2.76 mm.说明优化后的吊笼更不容易与施工升降机的激振频率产生共振，发生共振时的变形量也有了一定的减小.由此可见，吊笼优化后的模型在防止共振和结构稳定性方面都有更佳的表现.