基于DOE的电机多目标多变量快速参数化设计分析

杨伟涛

(惠而浦(中国)股份有限公司,合肥 230088)

0 引 言

随着科学技术的发展和人们生活水平的提高,大家对家用电器的性能等要求越来越高。另外,随着工业自动化、航空航天、武器装备、舰船潜艇等不断发展,人们对电机性能以及节能环保的要求也越来越高,因此为了进一步提高电机性能,对电机的多变量多目标优化设计就变得尤为重要。

ANSYS Maxwell有限元仿真软件中的参数化扫描优化方法是近年来在电机设计中常用的一种方法。特别是近几年比较火热的OptiSlang。文献[3]采用此方法对电机进行了优化,但需要建立庞大的参数化模型,并进行大量且复杂的运算才能得到所需的优化方案。过程操作繁杂,对运算设备要求较高,且需要大量的计算时间。

Taguchi法是一种较为新颖的局部优化算法,对比其他局部优化算法,它可实现多目标优化,并且在运用正交实验的实验方法后,能在较少的实验次数下给出多目标设计的最优参数组合。文献[4] 采用此方法对电机进行了优化,但没有给出各变量与优化目标间的定量关系,以及在预测刻画模型的帮助下推导出精准的最优变量组合,给出最佳方案。

本文以一台9槽6极洗碗机用水泵电机为例,选取了绕组匝数、铁心高度、槽口大小、气隙直径、气隙大小、定子齿宽、定子齿高7个参数为变量,以交直轴电感、反电动势为优化目标,通过基于实验设计(DOE)思想的多目标多变量的电机快速参数化优化方法,实现了通过16次的部分析因实验设计完成了常规参数化扫描最少2 187个节点的设计目标,大大节约了项目资源,提高了设计人员的设计效率,并缩短了项目的交付周期。另外,还科学地给出了各变量与优化目标间的定量关系,提高了设计人员对产品的理解以及经验设计和理论设计的水平。

1 DOE在电机多目标多变量参数化分析上的应用

基于实验设计(以下简称DOE)的电机多目标多变量参数化分析步骤如下:

1)选定优化目标,并基于理论分析、设计经验、专家意见等确定与优化目标相对应的参数变量。

2)根据确定的参数变量,制作实验因子设置表,表中需要给出各实验因子的上下水平,此上下水平的设置一般基于理论公式推导、设计经验、专家意见等。同时表中还需要给出各因子与优化目标之间的理论逻辑关系,以及最终的目标变化趋势。

3)根据以上确定的参数变量,制作各参数变量的实验因子关系图,用以指导后期的实验工作,并且便于后期相关人员了解当时的实验策略。

4)根据实验因子关系图进行相应实验,并正确记录相应数据。

5)通过专业的数据分析软件对实验数据进行分析处理,找出影响优化目标的关键因子,并确定其相互间的定量关系,最终通过预测刻画器给出最优方案。

6)对最优方案进行仿真或样机验证,确认是否满足优化目标。

本文案例是基于一款洗碗机用水泵电机,原始方案如图1所示,客户要求在保证电机槽极比、定子铁心外径、反电动势(128 V)等参数不变的前提下将电感从98 mH降低到72 mH,以达到提高电机性能和最大输出功率的目的。

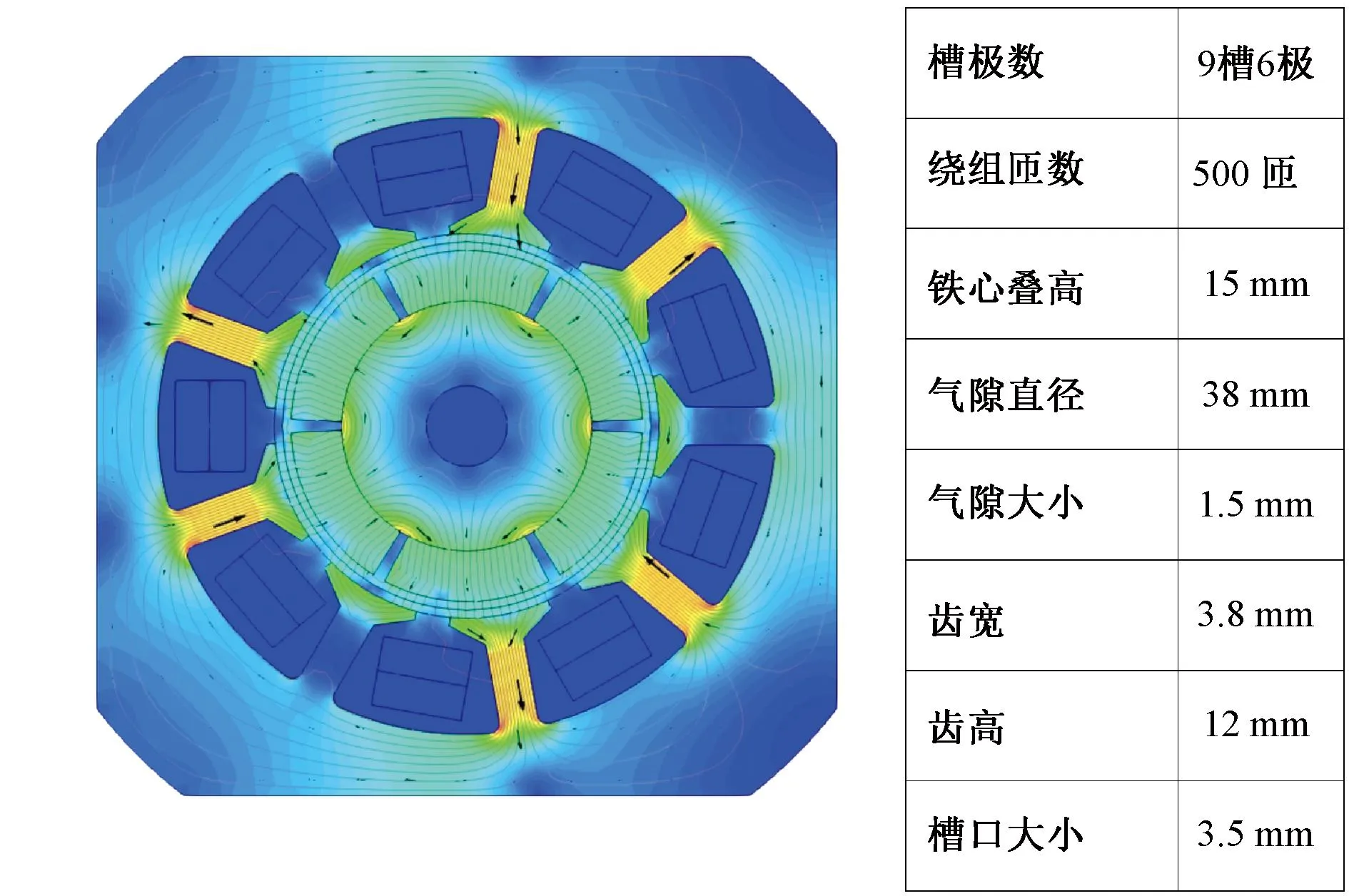
图1 原始方案

首先,通过以往设计经验以及理论公式推导,找出影响优化目标的相关因子。表述反电动势与各参数间相互关系的公式推导过程如下:

E=4.44fkwNphΦ

(1)

(2)

将式(2)代入式(1),得到式(3):

(3)

式中:μ0为气隙磁导率;f为频率;i为电流;L为气隙高度;r为气隙半径;kw为绕组系数;Nph为每相串联总匝数;g为气隙大小;p为极对数。

由式(3)可知,在不考虑饱和以及在极对数、频率、绕组系数、电流等参数一定的情况下,反电动势的大小与气隙高度、气隙半径成正比,与每项串联总匝数的平方成正比,与气隙大小成反比。

表述交直轴电感与各参数间相互关系的公式推导过程如下:

(4)

(5)

将式(5)代入式(4),得到式(6):

(6)

式中:Lq为交轴电感;Ld为直轴电感;La1为漏电感分量;Laa0为定子自感的气隙分量。

由式(6)可知,在不考虑饱以及在极对数、绕组系数等参数一定的情况下,交直轴电感的大小与气隙高度、气隙半径成正比,与每项串联总匝数的平方成正比,与气隙大小成反比,同时受漏电感分量大小的影响。

考虑到受磁路饱和、槽满率、漏磁通等的影响,以及由式(3)和式(6)推导分析得出的结论,本实验设计将绕组匝数、定子铁心高度、气隙直径、气隙大小、定子齿宽、定子齿高、槽口大小作为实验因子,具体实验因子的高低水平设置、理论趋势预测等如表1所示。

基于以上分析,并考虑到实验资源和项目周期的影响,本实验设计采用7因子2水平16次的部分析因实验策略,另外,根据正交实验设计思想,在保证各因子上下水平设置平衡的情况下设计出了具体的实验因子关系图(FRD),如图2所示。

根据以上实验策略,通过专业的电机设计软件,分别进行上述16次的电机设计仿真,得出的实验数据,具体如表2所示。

图2 实验因子关系图

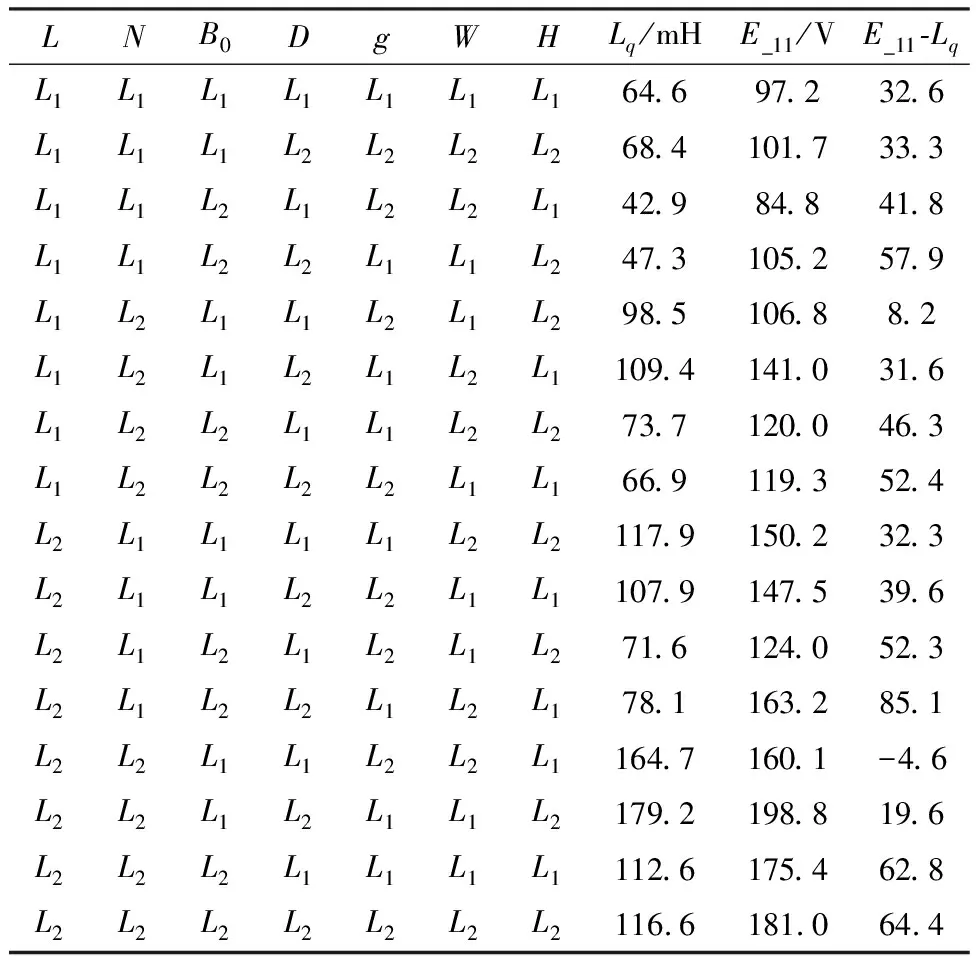
表2 实验数据

基于以上实验数据,通过专业的数据分析软件,如Jmp、Minitab等,对交轴电感Lq和线线间反电动势E_ll的实验数据分别进行拟合模型分析,得出如图3、图4所示的参数估计值。

图3 部分析因实验电感排序后的参数估计值

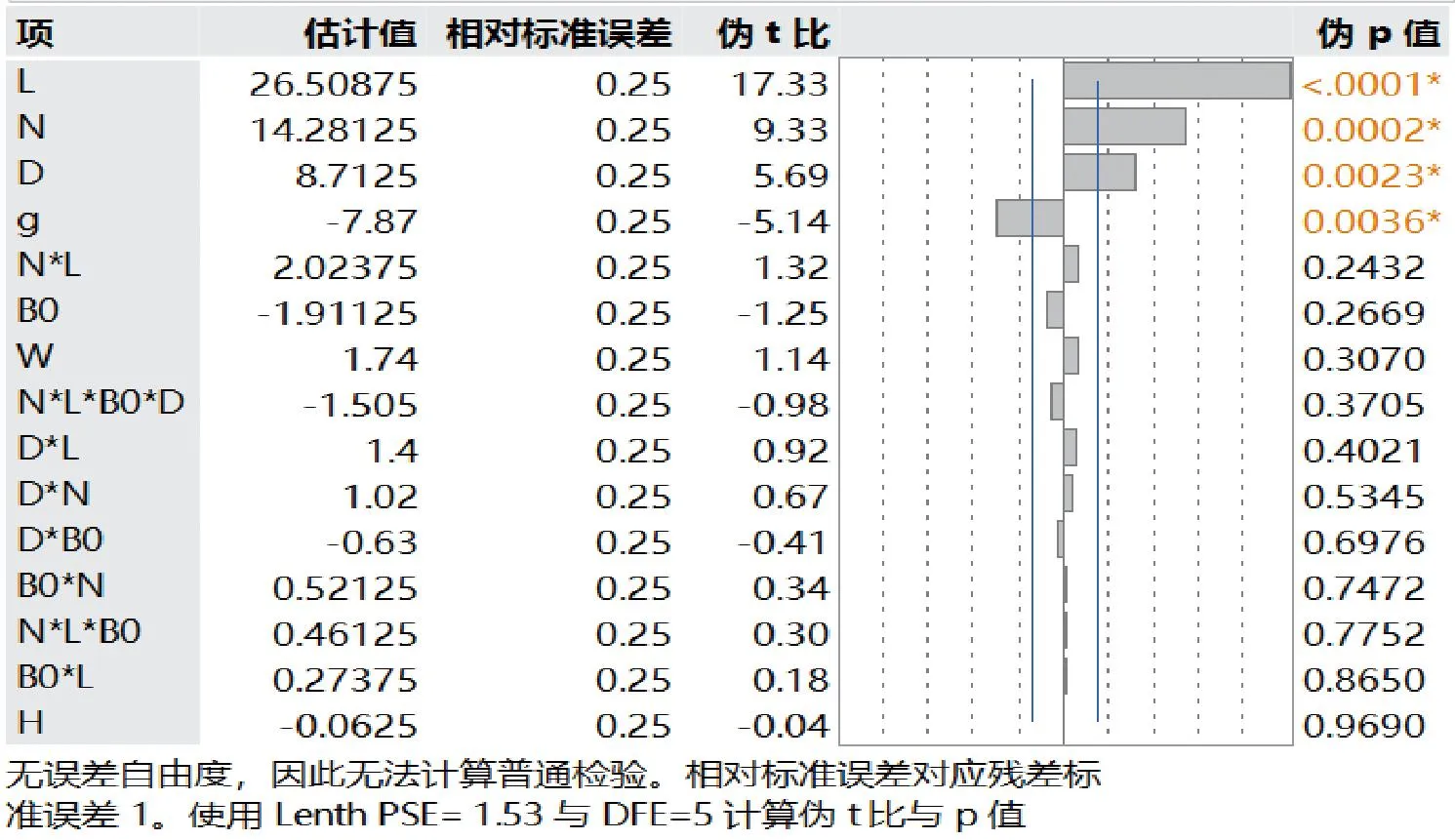
图4 部分析因实验反电动势排序后的参数估计值

如图3所示,根据P小于等于0.05的原则,我们可以得出影响电感的关键因子从大到小分别为定子铁心高度、绕组匝数和槽口大小,其中交轴电感Lq与定子铁心高度、绕组匝数成正相关,预测公式系数分别为23.56和20.17,与槽口大小成负相关,预测公式系数为-18.81。

如图4所示,根据P小于等于0.05的原则,我们可以得出影响反电动势的关键因子从大到小分别为定子铁心高度、绕组匝数、气隙直径和气隙大小,其中线线间反电动势E_ll与定子铁心高度、绕组匝数、气隙直径成正相关,预测公式系数分别为26.51、14.28和8.71,与气隙大小成负相关,预测公式系数为-7.87。

通过数据分析,我们还得到了交轴电感Lq和线线间反电动势E_ll与各实验因子的交互作用刻画图,如图5和图6所示。由此可知,各实验因子间无交互作用,可以不用考虑各因子间交互作用的影响。

图5 电感各因子间交互作用刻画图

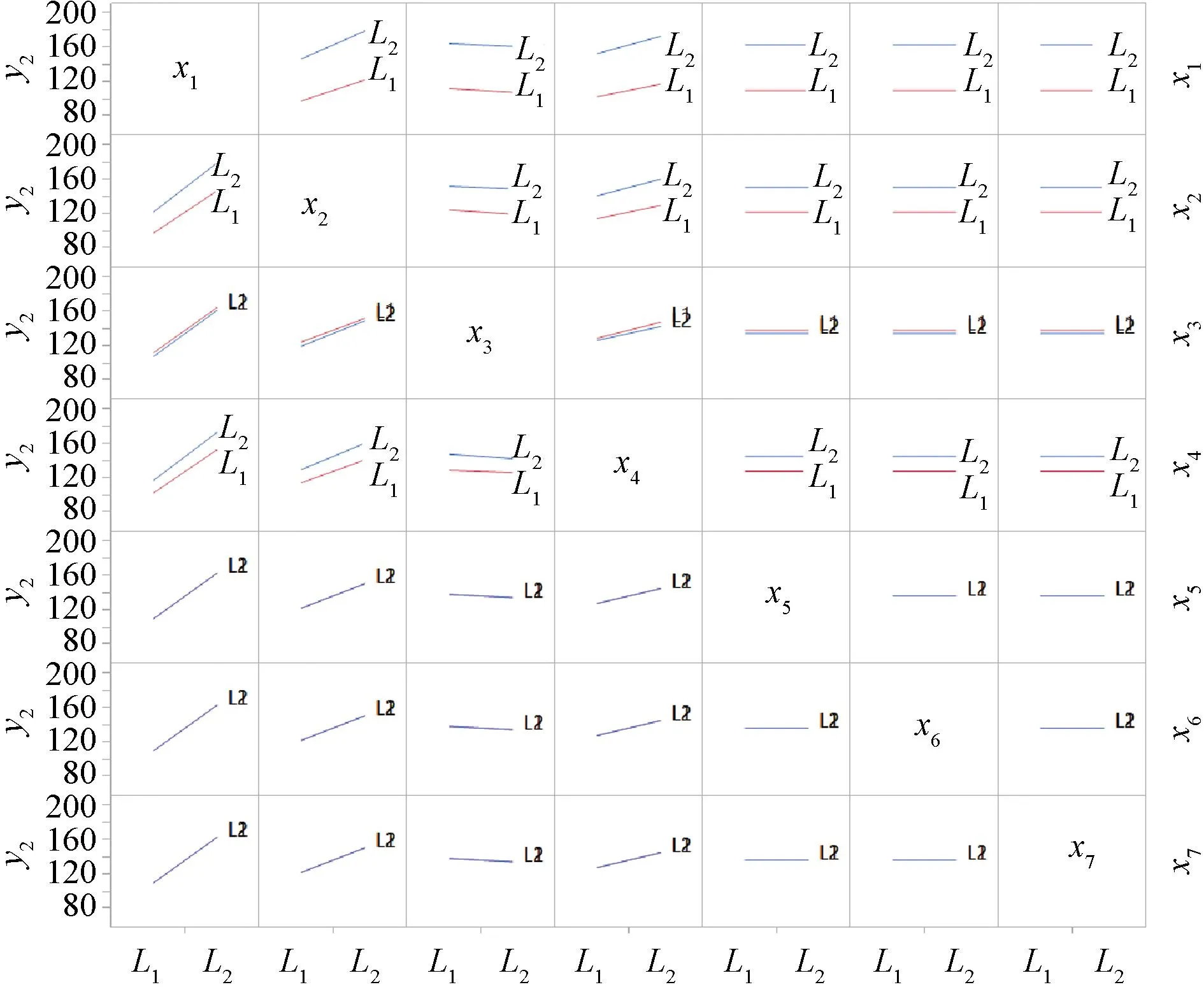
图6 反电动势各因子间交互作用刻画图

根据以上分析,考虑到各因子的预测系数以及成本因素,通过如图7所示的部分析因实验预测刻画器可知,要得到较大的反电动势、较小的电感值,即E_ll-Lq取较大值时,其最关键因子为槽口大小,且与其成正相关,因此槽口大小B0的系数取1,由表1实验因子设置可知,槽口大小B0系数取1时即B0=6 mm。

根据图7的预测刻画器,我们可以计算出,在绕组匝数取470匝、定子铁心高度14 mm、气隙直径40 mm、气隙大小1.2 mm、定子齿宽3.3 mm、定子齿高12.5 mm时,所得方案满足客户要求,此时Lq=69.8 mH,E_ll=128.6 V。

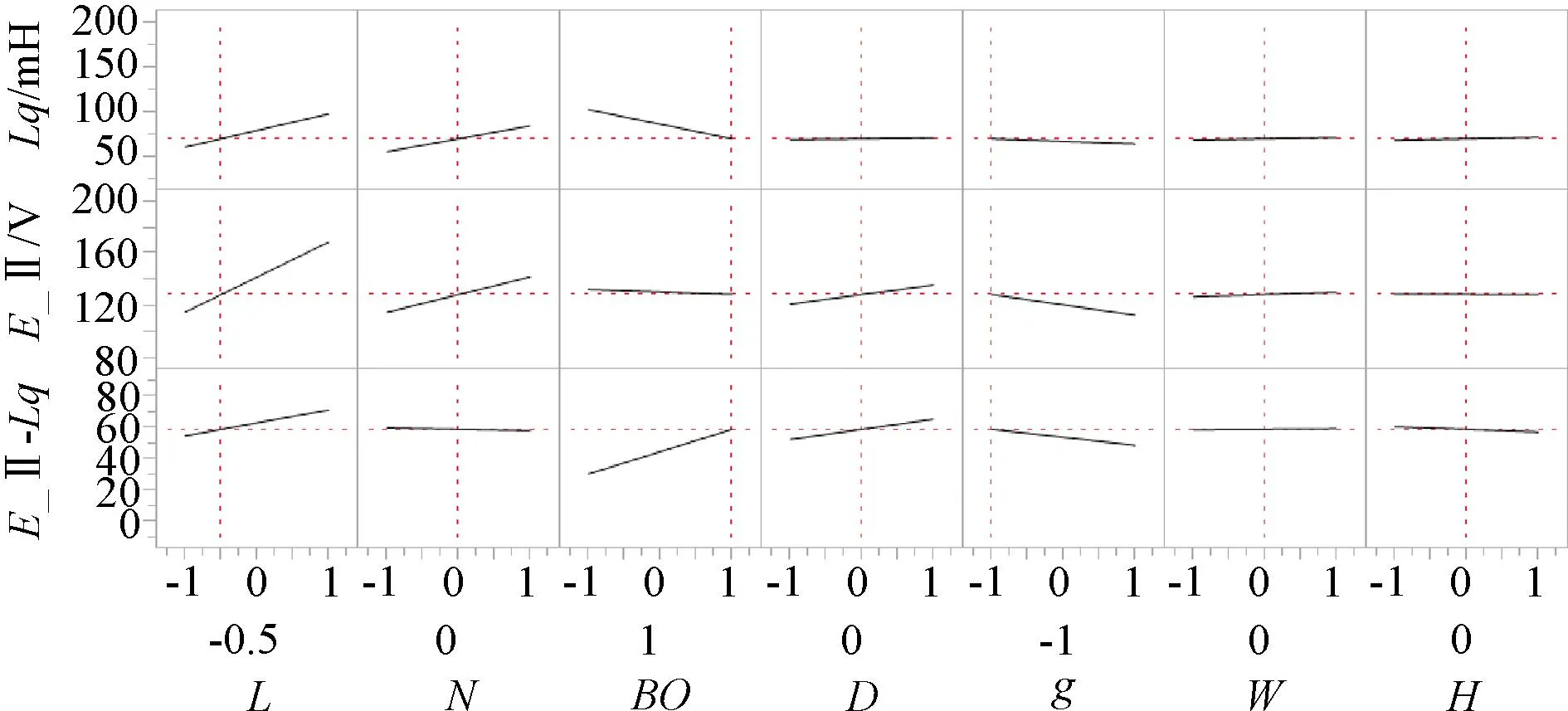
图7 部分析因实验预测刻画器

为验证7因子2水平16次的部分析因实验策略的可信度,本文还进行了7因子2水平128次的完全析因实验,并对实验数据进行分析,得到了完全析因实验排序后的参数估计值,如图8、图9所示,我们发现,影响电感的关键因子从大到小分别为定子铁心高度、绕组匝数和槽口大小,其中与定子铁心高度、绕组匝数成正相关,预测公式系数分别为23.87和20.25,与槽口大小成负相关,预测公式系数为-18.97。

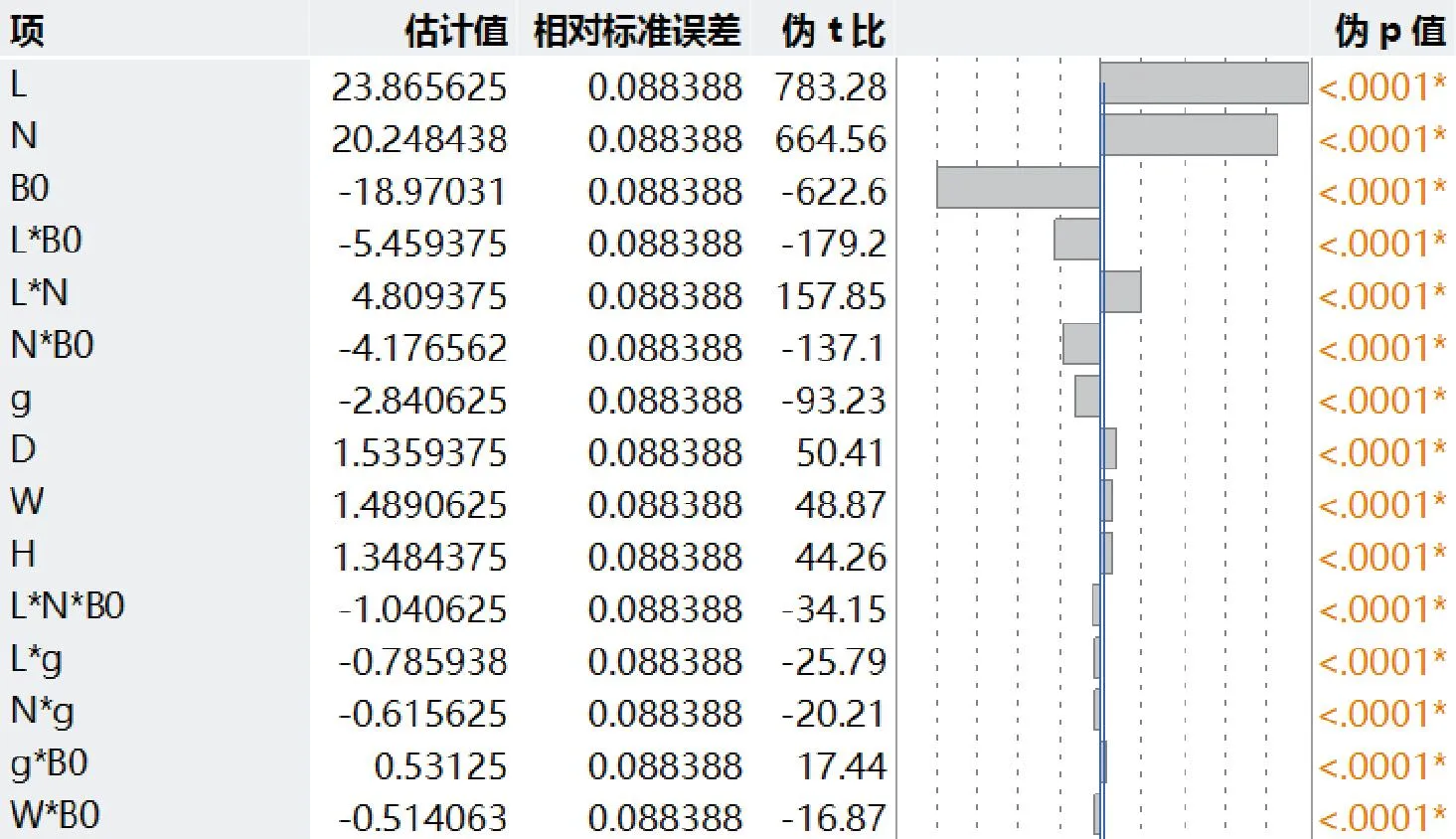
图8 完全析因实验电感排序后的参数估计值

影响反电动势的关键因子从大到小分别为定子铁心高度、绕组匝数、气隙直径和气隙大小,其中与定子铁心高度、绕组匝数、气隙直径成正相关,预测公式系数分别为26.7、14.49和8.64,与气隙大小成负相关,预测公式系数为-8.01。以上结果与部分析因实验策略下得到的结果基本相同。

图9 完全析因实验反电动势排序后的参数估计值

另外,根据完全析因实验的预测刻画图,如图10所示,同样在槽口大小6 mm绕组匝数470匝、定子铁心高度14 mm、气隙直径40 mm、气隙大小1.2 mm、定子齿宽3.3 mm、定子齿高12.5 mm时,Lq=69.1 mH,E_ll=128 V,其结果与部分析因实验策略下得到的结果基本相同。

图10 完全析因实验预测刻画器

为了验证实验设计思想在设计领域应用的可行性,作者还进行了常规的7个变量,每个变量设置3段,共2 187个节点的参数化扫描仿真实验,其结果如图11和图12所示。当槽口大小6 mm、绕组匝数470匝、定子铁心高度14 mm、气隙直径40 mm、气隙长度1.2 mm、定子齿宽3.3 mm、定子齿高12.5 mm时,Lq=68.9 mH,E_ll=129.8 V,与基于实验设计思想下的多参数化多目标仿真结果基本相同,证明了实验设计思想在设计领域应用的可行性。

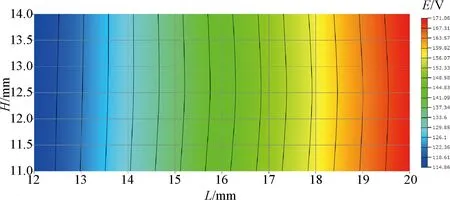
图11 线间反电动势

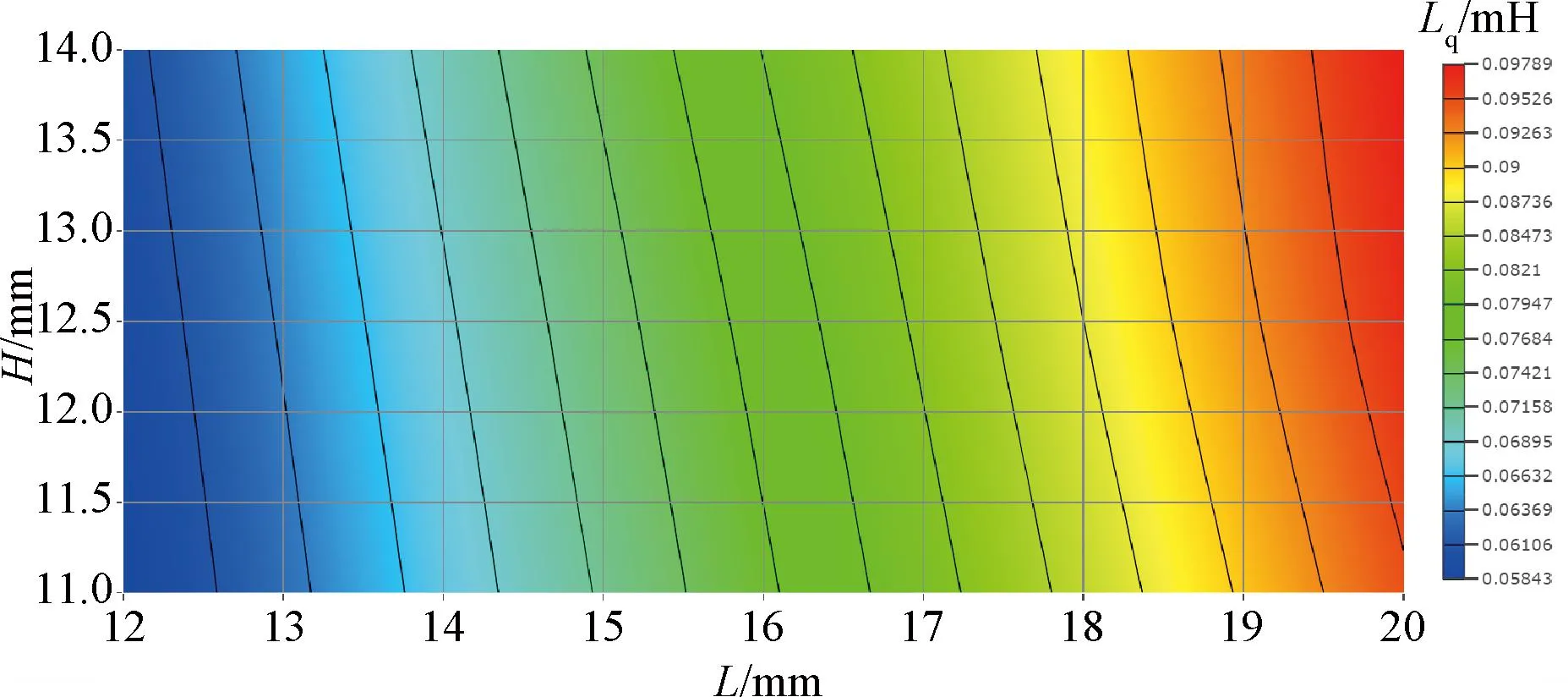
图12 交轴电感

2 实验设计分析结果与样机实测结果对比分析

根据16次部分析因实验设计、128次完全析因实验设计以及常规2 187个节点的参数化扫描,其所得结果基本相同,最终我们确定最优方案的相关参数取值如下:槽口大小6 mm、绕组匝数470匝、定子铁心高度14 mm、气隙直径40 mm、气隙长度1.2 mm、定子齿宽3.3 mm、定子齿高12.5 mm。根据以上参数取值,我们制作了相应的手板样机,如图13所示。并将实测结果和仿真结果整理如表3所示。

图13 样机

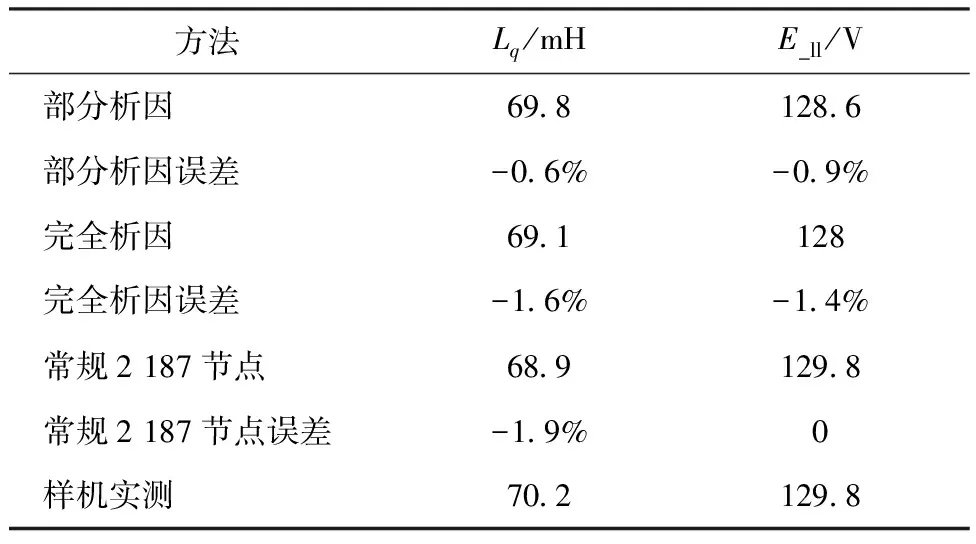
表3 DOE分析结果与样机实测结果对比

由表3可以看出,16次部分析因实验设计结果、128次完全析因实验设计结果、常规2 187个节点的参数化扫描结果与样机实测结果的误差均小于>5%,说明基于实验设计思想下的电机多目标多变量的快速参数化设计分析的方法是可靠的,并且在保证同等设计精度的同时可以节约大量的设计资源和设计时间,大大提高了设计人员的设计效率,缩短了项目的交付周期,同时,本方法还科学的给出了各因子间的定量关系,提高了设计人员的理论和经验设计水平。

3 结 语

通过以上理论分析和实际测量结果对比,我们可以得出以下结论。

(1)基于DOE的电机多目标多变量的参数化优化方法可以快速地完成参数化寻优设计,方法是可行的,结果是准确的;

(2)科学地给出各因子与优化目标间的定量关系,提高设计人员对产品的理解以及经验设计和理论设计的水平。

(3)本文案例用16次的部分析因实验设计策略完成了常规参数化扫描2 187个节点的设计目标,大大节约了开发资源,提高了设计人员的设计效率,缩短了项目的交付周期。

(4)由于只需要较少的实验次数就可以完成多变量的寻优目标,在不建立庞大的二维或三维参数化模型的情况下,可以采用二维有限元,甚至是三维有限元的设计仿真方法进行多目标多变量的参数化分析,大大提高了设计精度。

(5)由于其只需要较少的实验次数就可以完成多变量的实验目标,所以对设计仿真的硬件要求不高,可大大降低公司对设计仿真硬件的投资。