振动筒压力传感器振荡系统仿真设计与测试

姚敏强,张 斌,康志宏,宋继红

(1.太原航空仪表有限公司,山西太原 030006;2.空军装备部驻太原地区军事代表室,山西太原 030006)

0 引言

高精度振动筒压力传感器,在气象、测控等领域的大气参数测量中具有广泛应用[1]。该类型压力传感器在生产过程中,存在批次合格率低和性能不稳定的现象。本文针对压电激励型振动筒压力传感器,基于正向设计思路,对其振荡系统进行理论分析,同时采用ANSYS和Cadence仿真软件对振荡系统各组成模块进行仿真设计,并依据仿真设计结果搭建实物测试平台进行测试验证。采用理论和工程实践相结合的方式,重点论述了振荡系统阻尼特性、压电陶瓷片性能指标和振荡系统的建立条件等影响传感器工程化稳健性的因素,可以有效提升传感器工程化合格率和性能稳定性。同时,本文技术思路和设计方法对谐振系统[2]的设计和研究具有参考意义。

1 工作原理

1.1 振荡系统基本模块

振动筒压力传感器振荡系统基本模块,如图1所示,主要包括振动筒敏感元件,换能元件压电片、振荡电路等。振动筒敏感元件为谐振子,主要用于感受外界压力的变化,而输出不同的固有频率。换能元件利用压电片的正逆压电效应实现机械能与电能的转换。振荡电路配合谐振子实现振荡系统的相位条件和增益条件。

图1 振动筒压力传感器振荡系统基本结构

1.2 振荡系统谐振子数学模型

振动筒敏感元件受周期荷载激励时的二阶系统振动方程[3]为式(1)：

(1)

式中：x为谐振子位移;m为等效质量;c为等效阻尼;k为等效刚度;P0sinωt为周期激励荷载。

对二阶系统方程求解,稳态解为式(2)：

x(t)=C0A(ω)sin[ωt+φ(ω)]

(2)

其中：

C0=P0/k

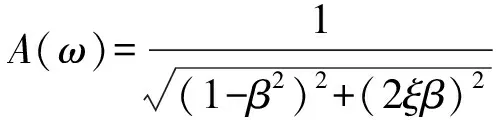
式中：C0为恒静力P0对系统产生的位移;A(ω)为幅值;φ(ω)为相移;β为频率比;ξ为阻尼比。

传感器发生谐振时,存在周期激励荷载的频率ω与振动筒敏感元件固有频率ωn接近,此时β→1,二阶系统的稳态解为式(3)

(3)

1.3 振荡系统正反馈条件时域分析

图2 振动筒敏感元件时域信号流图

综上,在周期荷载的频率ω接近固有频率ωn的前提下,为完成闭环系统正反馈振荡,要求满足式(4)和式(5)：

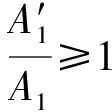
(4)

相位条件：φ′=2nπ(n=0,±1,±2,±3,…)

(5)

2 基于Ansys对振动筒敏感元件仿真分析

2.1 振动筒敏感元件建模

振动筒敏感元件为一端开口,另一端封闭的薄壁圆柱筒。考虑传感器性能指标要求振动筒敏感元件设计结构如图3所示,主要参数见表1。

图3 振动敏感元件设计结构

表1 振动筒敏感元件结构具体参数 mm

振动筒敏感元件材料选用3J53恒弹合金,材料基本性能参数参见中国航空材料手册[4],具体见表2。

表2 3J53性能指标

2.2 振动筒敏感元件预应力下模态分析

考虑振动筒传感器的稳定性、灵敏度和精度等指标要求[5],采用ANSYS中Model模块和Static Structural模块对振动筒敏感元件进行100 kPa预应力条件下(3,1)振型的模态分析。图4为100 kPa预应力下振动筒敏感元件(3,1)振型图[6]。(3,1)振型模态分析固有频率为9237.7512 Hz。

图4 100 kPa预应力下振动筒敏感元件(3,1)振型图

2.3 振动筒敏感元件谐响应分析

基于上述模态分析,考虑振动筒敏感元件筒体内部摩擦、压电片胶接、筒体焊接等接触条件,采用Ansys中Harmonic Response模块,针对振型(3,1)固有频率为9237.7512 Hz进行不同阻尼比下谐响应分析。图5为不同阻尼比下扫描频率与响应相位的关系。图6为不同阻尼条件扫描频率与响应幅值关系。不同阻尼比条件下扫描频率接近固有频率时品质因素、响应幅值和响应相位见表3。

表3 不同阻尼比条件下品质因数、响应幅值和响应相位

在扫描频率接近振型(3,1)的固有频率9237.7512 Hz时,品质因素和响应幅值随阻尼比的增大而减小,在固有频率附近响应相位的斜率随阻尼比的增大而减小,在扫描频率接近固有频率时,相位差约为-92°。从图5、图6可以看出,阻尼比越大传感器的灵敏度、稳定性越差,传感器装配过程应充分考虑阻尼对传感器性能的影响。在实际生产中,可以通过优化振动筒敏感元件结构的边界条件、合理选择压电陶瓷片胶接材料的弹性模量和压电陶瓷片的贴片位置提升振荡系统的阻尼特性,进而有效提升传感器的性能稳定和生产合格率。

3 振动筒敏感元件信号传输分析

图7 换能元件压电陶瓷片

换能元件选用压电陶瓷片PZT-5A,如图7所示。压电片胶接于振动筒敏感元件内表面,如图1中位置所示。利用压电片的正压电效应和逆压电效应完成振动筒敏感元件和谐振电路之间机械能与电能转换[7]。忽略压电片的离散性和胶接影响,发生谐振(ω与ωn非常接近)时,依据二阶系统稳态解,系统放大倍数只与系统阻尼比ξ有关。依据正逆压电效应关系和胡克定律,μ1、μ2幅值关系可表示为

(6)

从式(6)可以看出,压电陶瓷片和振动筒敏感元件胶接后,主要考虑其力学特性指标弹性模量,弹性模量直接影响振荡系统建立的增益条件,进而影响振荡系统的起振过程和传感器的性能稳定。在传感器设计过程中,合理选择压电陶瓷片的弹性模量可提高传感器的性能稳定性。

根据中国航空材料手册[4]压电陶瓷片PZT-5A的弹性模量为EPZT-5A=56 GPa;振动筒敏感元件的弹性模量为E=192 GPa。A2/A1约为0.29。闭环系统增益条件为A′1/A1≥1,振荡电路的增益条件为A′1/A2≥3.4。

±1,±2,±3,…)。

4 振荡电路仿真设计

4.1 振荡电路结构组成

振荡电路结构组成主要包括3部分：电荷放大电路、相位调整电路和放大电路。振荡电路原理图如图8所示。

压电陶瓷片在振荡电路中主要考虑其电学特性,可以等效为电容C1、C4,压电片的尺寸和机电转换系数直接影响振荡电路的增益和相位。考虑压电效应和阻抗匹配等问题,第1级采用电荷敏感放大电路;考虑相位条件,第2级采用相位调整电路;考虑增益条件,第3级采用放大电路。对每一级电路传输函数分析如下：

第1级电荷放大电路传输函数为

(7)

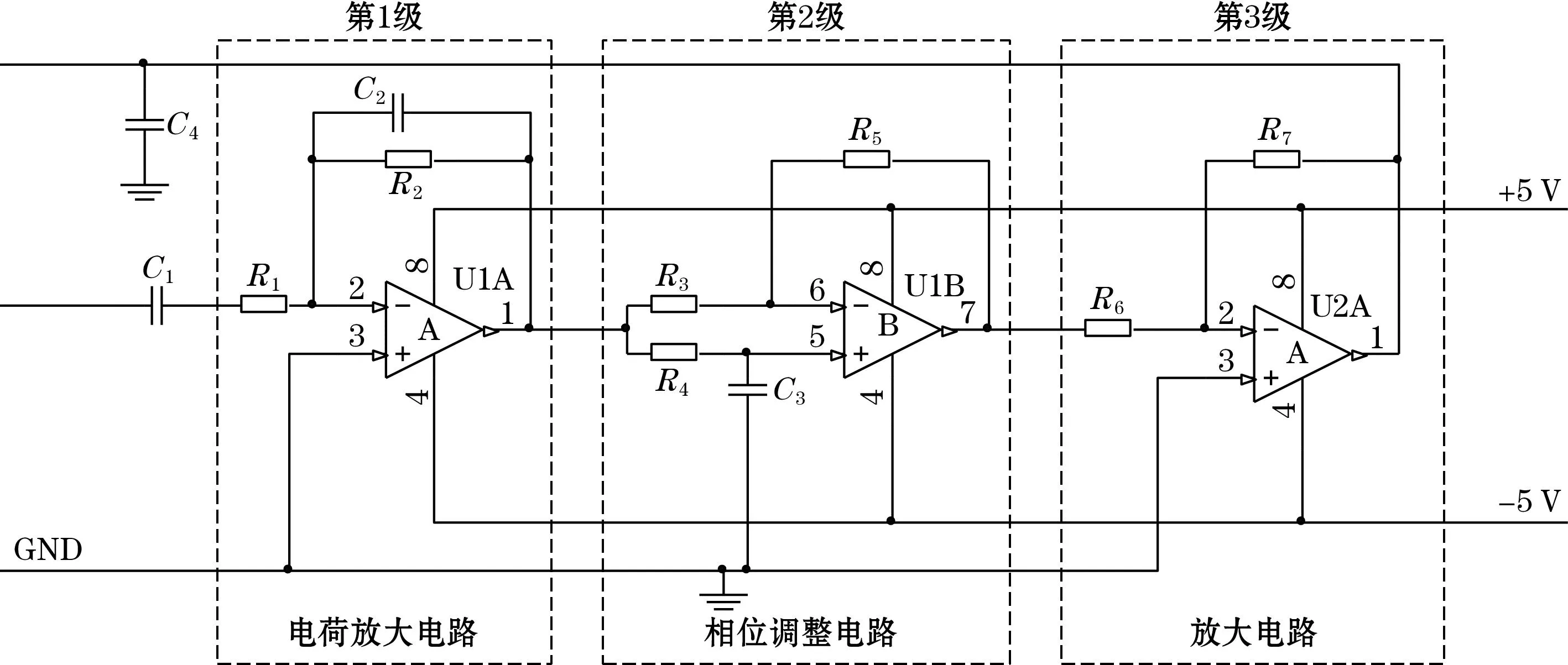
图8 振荡电路原理图

第2级相位调整电路传输函数(R3=R5)为

(8)

第3级放大电路传输函数为

(9)

4.2 振荡电路仿真分析

基于cadence中PSpice工具对上述振荡电路进行幅频特性和相频特性仿真分析。仿真结果如图9、图10所示。

图9 振荡电路幅频特性

图10 振荡电路相频特性

通过对振荡电路仿真分析和参数优化,在接近固有频率频率为9.267 kHz处,振荡电路的增益为34.26 dB,相位为-273.512°,该结果满足振荡系统对振荡电路增益和相位条件要求。

5 振荡系统测试

5.1 振动筒敏感元件测试

通过上述理论和仿真分析,在常温常压下采用网络分析仪E5061B对振动筒敏感元件和换能元件组成的系统进行开环测试,测试平台如图11所示,测试结果如图12所示。

图11 振动筒敏感元件测试平台

图12 振动筒敏感元件幅频相频实测图

从图12可知,在常温常压下振动筒敏感元件的固有频率为9.018 kHz,增益为0.217 dB,相位为-81°。在考虑试测大气压以及工艺偏差的情况,测试结果与仿真分析相吻合。

5.2 振荡电路实测

在常温常压下,采用网络分析仪E5061B对振荡电路幅频相频特性实测,测试平台如图13所示,测试结果如图14所示。

图13 振荡电路测试平台

图14 振荡电路幅频相频特性测试

从图14可知,振荡电路在振动筒敏感元件的固有频率为9.018 kHz,增益为30.191 dB,相位为96°(当测试值超过-180°,网络分析仪输出结果加360°)。振荡电路在固有频率处增益和相位条件略有偏差,但满足振荡系统振荡条件设计要求。

5.3 振荡系统测试

在±5 V供电条件下,在振荡系统各组成模块仿真设计和工程化测试验证的基础上,对由振动筒敏感元件、换能元件和振荡电路组成的振荡系统进行阻容微调,并用示波器测试该振荡系统的激励端,起振过程如图15所示,起振后工作频率为9.018 kHz,工作在振动筒敏感元件固有频率处,起振过程时间大约200 ms,在起振过程中信号幅值由小变大,并且逐渐饱和,达到运放的供电电压±5 V,起振时间满足工程化实际应用需求。

图15 振荡系统起振过程

6 结论

本文基于正向设计思路,对高精度压电激励振动筒压力传感器振荡系统进行了理论分析、仿真设计和工程化测试验证。重点论述了振荡系统阻尼特性、压电陶瓷片力学、电学性能指标和振荡系统的建立条件等影响传感器工程化应用和系统稳健性的因素,并结合工程化实践给出了振动筒敏感元件边界条件,压电陶瓷片弹性模量、尺寸、贴片位置选择和力学电学参数,振荡电路元器件参数和工艺要求等优化设计建议。