陀螺旋转式振动能量收集器的结构设计与优化

吕鑫盛,彭 晗,顾天逸,孙寒燚,高 凯,王劭菁,徐 鹏

(1.强电磁工程与新技术国家重点实验室,华中科技大学电气与电子工程学院,湖北武汉 430074;2.国网上海市电力公司电力科学研究院,上海 200437)

0 引言

无线传感器网络(wireless sensor network,WSN)是由分布在监测区域内的大量传感器节点通过无线通信组成的一种网络系统,在安全、环境等领域有广泛应用[1]。目前,WSN节点主要依靠化学电池供能,但化学电池使用寿命短、储能有限的问题,严重影响了WSN节点的长期稳定运行。一个解决方案是利用基于振动的能量收集技术[2-3]实现WSN节点自供电[4]。

现有的振动能量收集技术采取惯性滑块[5]、惯性球[6]、惯性摆[7-8]等方式俘能。环境中的低频振动,例如波浪运动,具有随机、不规则的特性。在低频振动中,利用谐振俘能的惯性滑块和惯性摆结构的输出功率受限,而惯性摆结构会出现复摆和旋转2种运动方式,需设计复合式的能量收集器,装置复杂度增加。

为实现低频振动条件下稳定的旋转式能量收集,本文研究一种陀螺旋转式振动能量收集器的结构设计与优化,该装置由轨道、转子、线圈绕组和整流降压电路构成,利用陀螺进动效应和摩擦力,将外界低频振动转化为高频转子旋转,收集转子旋转能量为WSN节点供能。

陀螺旋转式振动能量收集器可以结构近似的腕力球作为模型,以分析其动力学运动机制[9-11]。线圈作为机电能量转换元件,是决定取能输出功率和输出电压幅值的关键元件[12-13]。线圈需与永磁转子配合设计以实现有限体积下输出功率的提升。现有的电磁式旋转能量收集器[7-8]中,转子一般为定轴旋转,在转子扇叶中对称嵌入永磁体,并在正对于永磁体磁极的近处放置线圈阵列。而陀螺旋转式振动能量收集器中,转子做旋转运动的同时,还在轨道上做进动运动[11],这使得现有的定轴旋转式的转子与线圈结构不再适用。

线圈绕组的匝数及其排布方式的设计需要满足多个目标：额定输出功率、高能量转换效率和转子运动稳定性,而这3个目标间又存在相互影响。研究线圈排布方式的多目标优化,是能量收集器结构设计与优化的核心环节。

现有陀螺旋转式能量收集工作[14-17]大多围绕旋转式能量收集的机构展开,聚焦旋转式机-电转换特性,未深入研究线圈与磁铁的配型与选型,也未对线圈排布方式进行设计优化,造成能量转换效率偏低、能量收集装置设计普适性较差等问题。

为解决上述问题,本文从运动特性出发,分析了装置的电磁特性。球形磁铁在旋转和进动运动中具有较好的稳定性,且可以与圆形线圈绕组始终维持均匀气隙,本文提出了球形永磁转子和与之匹配的圆形线圈绕组的选型方案。借助仿真模型分析了能量收集器工作特性和稳定性条件,并据此设计了线圈排布算法,可在给定工作条件约束下优化线圈结构。能量收集器结构设计优化方法兼顾了转子运动稳定性,输出功率的持续稳定和高能量转换效率,可为WSN持续稳定供能。

1 陀螺旋转下机-电理论模型分析与仿真

文献[11]使用混合动力学系统(HDS)描述转子的动力学现象,建立了HDS的数学模型和仿真模型,并通过实验进行了验证。本文在文献[11]中的HDS模型基础上建立了陀螺旋转下机-电理论模型和仿真模型,系统结构图如图1所示。

图1 系统结构

1.1 转子动力学模型

图2为陀螺旋转式振动能量收集器的基本结构。转子两端由轨道支撑,轨道的高度略大于转子轴的直径。转子在轨道上可以旋转和进动,但其章动被限制在小范围内。线圈固定于内侧线圈支架上,线圈支架不与转子接触,不随转子旋转,如图3所示。

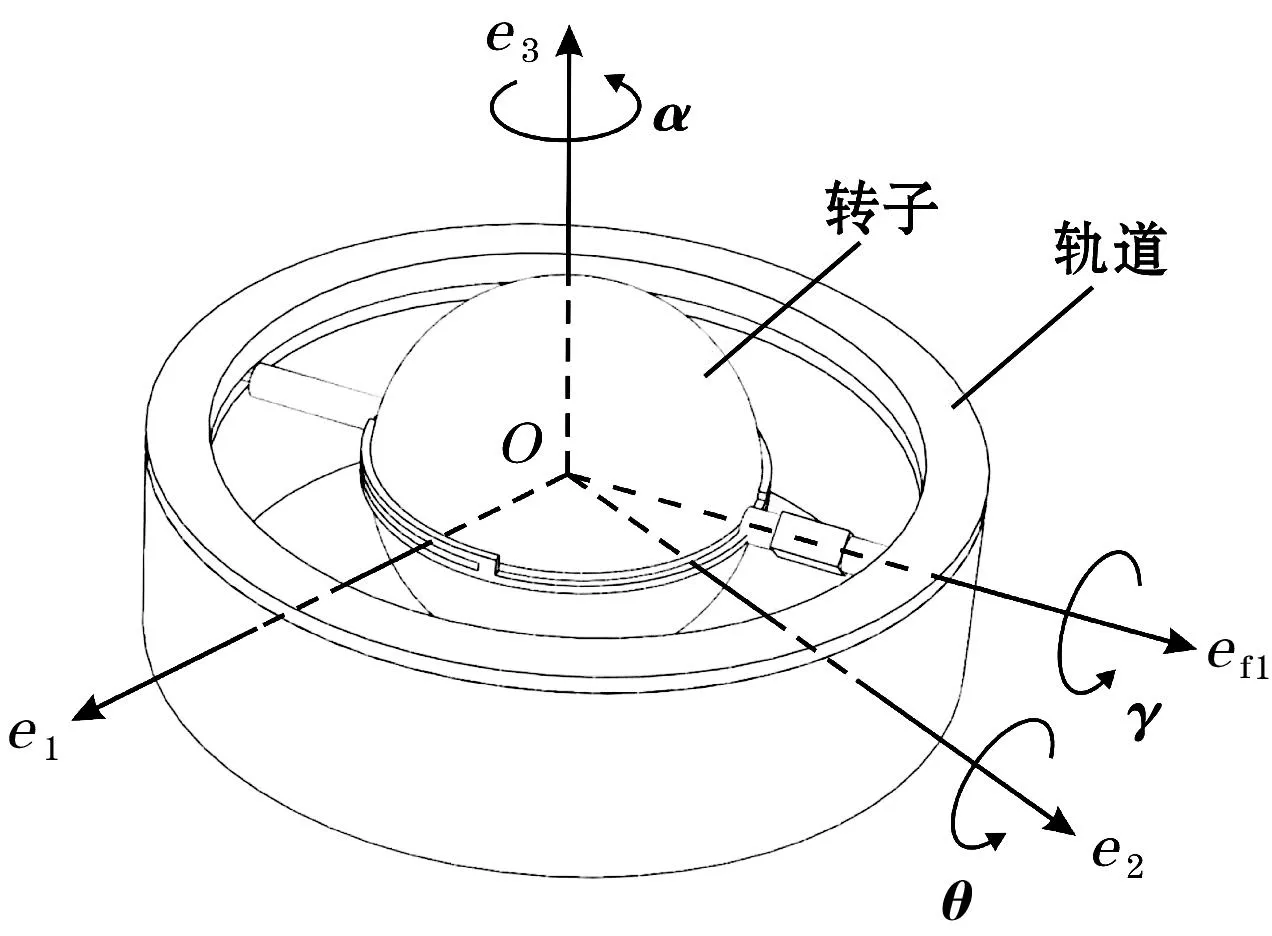
图2 陀螺旋转式振动能量收集器基本结构图

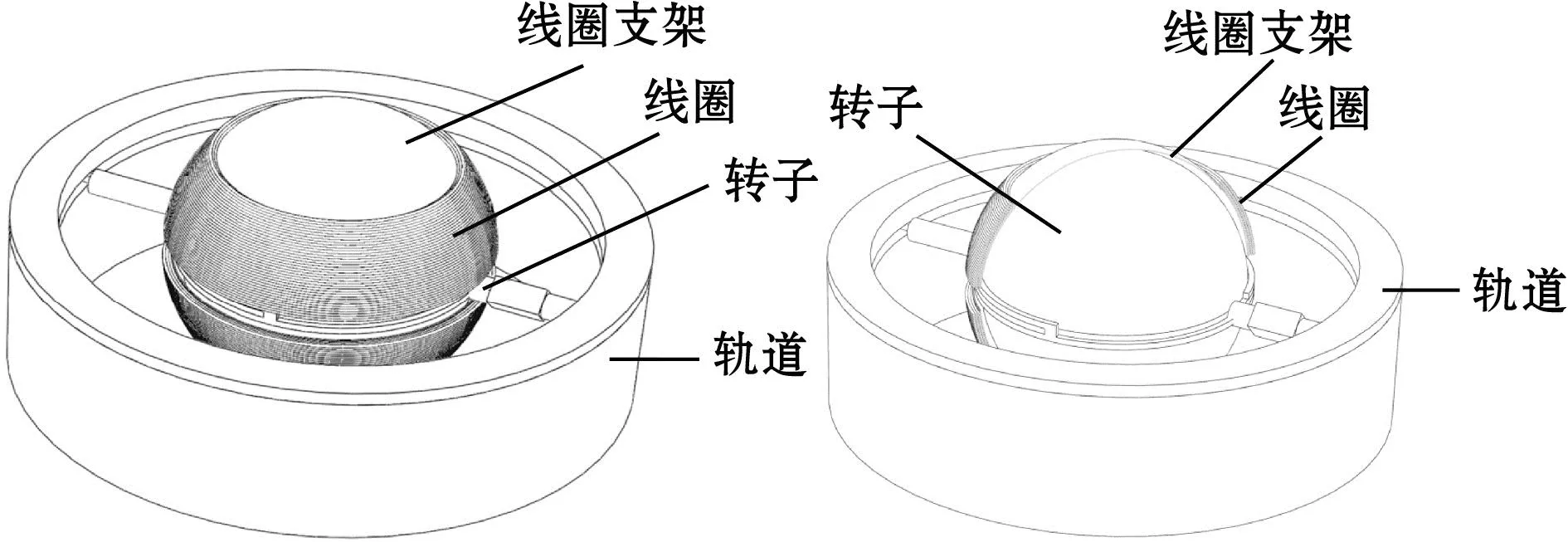
(a)整体结构图 (b)局部剖视图图3 转子、轨道、线圈和线圈支架组装图

本文的动力学模型所用的坐标系的具体含义如表1[11]所示。定义模型的输入角为θ,进动角为α,章动角为δ,旋转角为γ。转子可绕轴ef1旋转,绕轴et3进动,绕轴ef2章动。

受到外界不均匀的低频振动作用时,能量收集器做位移和翻转运动。由于转子转轴两端上下受轨道限制做小幅度章动,但在轨道内可自由进动和旋转,故转子绕轴旋转运动主要受翻转运动影响,受位移运动影响较小。仅考虑翻转运动对能量收集器输入角θ的影响,并假设其符合简谐运动的形式,作用在轴e2上,θ可表示为

θ=θ0sinΩt

(1)

式中：θ为输入角;θ0为θ的振幅;Ω为输入角角速度。

1.2 对动力学模型添加电磁阻尼修正

定义电磁转矩Tem为转子磁通与线圈电流相互作用而在转子上形成的旋转力矩,Tem在发电机中表现为电磁阻尼,表示为

(2)

式中：σe为电磁阻尼系数;Pem为转子电磁功率。

陀螺旋转式振动能量收集装置体积较小,转子旋转频率较低,转子为永磁材料且剩余磁通密度较大,可认为转子电磁功率Pem与线圈及电路闭合回路消耗功率Pcir近似相等,得到σe的表达式：

(3)

考虑电磁阻尼,将转子旋转和压力产生的力矩Mdm[11]修正为

(4)

将修正后的Mdm替换文献[11]中的Mdm,得到转子的运动特性方程[11]。

1.3 转子动力学特性仿真

表2 转子动力学模型的输入条件和初始条件

图4 最大电磁功率与稳定旋转角速度关系

图5 转子空载运动特性

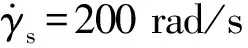
图6 转子满载运动特性

1.4 转子电磁特性仿真

1.4.1 转子空间磁场分布仿真

为了确保转子能长期稳定运动工作,同时实现较高的能量收集效率,能量收集器机械结构应具有转子转动惯量较大,气隙较小且均匀,整体体积较小等特点。综合考虑以上需求,本文选择钕铁硼强磁材料的球形磁铁作为转子。钕铁硼强磁材料剩磁、密度较大,而球形转子在旋转和进动过程中可以保持气隙始终较小且均匀,具有很好的性质。本文选定的磁铁性能型号为N35,剩磁感应强度1170～1210 mT。

球形磁铁有一对磁极,采用COMSOL Multiphysics对球形磁铁的空间磁通密度分布进行仿真分析,如图7所示,内部剩磁较大且方向一致,磁通密度模在两极附近较大,而在分界面附近接近于0。

图7 球形磁铁空间磁通密度分布

如图3所示架设线圈,结合图7可知,当气隙很小时,通过调整线圈半径可以使磁感线几乎全部以同一方向穿过线圈平面,再从平面外部返回,从而在线圈平面内得到最大的磁通变化率。

1.4.2 转子空间感应电场分布仿真

由麦克斯韦方程组可知,单匝线圈感应电动势可用Ecoil=∮LE·dl计算,E为空间某处感应电场。因此借助转子空间感应电场分布仿真数据可以计算架设在空间内任意一点的单匝线圈的感应电动势。

采用COMSOL Multiphysics对能量收集器进行仿真。输入参数及初始参数如表3所示,转子材料参数如表4所示。

转子旋转过程中,空间中变化的磁场产生变化的感应电场。空间感应电场ef1与ef2组成平面分量模Exy分布图如图8所示。当转子NS极连线和轴ef1与ef2组成的平面重合时,Exy达到幅值Exym。感应电场在转子磁极附近较强。

图8 空间感应电场分量模Exy分布图

2 球形结构下线圈设计与优化方法

2.1 线圈形状设计

为了获得持续稳定的感应电压,同时维持均匀的气隙,将每匝线圈形状设计为圆形,圆心和轴e3与每匝线圈闭合平面交点重合,如图3所示。这样设计使感应电压频率只与fspin相关,与fpre无关,呈现正弦波形。

2.2 线圈排布算法

球形结构下线圈设计的目标为实现能量收集器在额定输出功率下的稳定运行,同时保持较高的能量转换效率。

本文结合转速寻优以及线圈排布寻优两个目标,设计了一种基于遗传算法的线圈排布算法。通过迭代给出最优解下的转子转速及线圈排布方案,线圈电压等输出参数。算法的寻优过程如图9所示。

图9 线圈排布算法寻优过程

线圈排布算法通过调整每匝线圈的空间位置。调整线圈的总感应电动势和内阻,与后级电路配合输出额定功率,对得到的解进行优化得到较高的能量转换效率和较低的外界输入能量要求。

2.3 线圈排布优化设计

采用COMSOL Multiphysics进行仿真测试。转子旋转角速度=125.7 rad/s,使用的铜导线直径为0.25 mm。转子材料参数如表4所示。设定目标线圈电压有效值Ecoil=1.1 V。

一种常规的线圈排布方式如图10所示。经仿真测试,该排布方式下最小线圈匝数N=62,线圈内阻Rcoil=3.7 Ω。

图10 优化前线圈排布方案

使用线圈排布算法对目标线圈电压有效值进行优化,得到的线圈排布方案如图11所示,线圈匝数N=53,线圈内阻Rcoil=2.6 Ω。

图11 优化后线圈排布方案

在输出相同线圈电压时,使用优化算法后得到的线圈排布方案与优化前相比,线圈匝数减小14.52%,线圈内阻减小29.7%,输出功率提高42.31%,优化效果明显。

3 仿真与系统设计

3.1 电能变换电路设计

本文采用以LTC3119芯片为主体的电路进行降压变换,电路结构如图12所示。

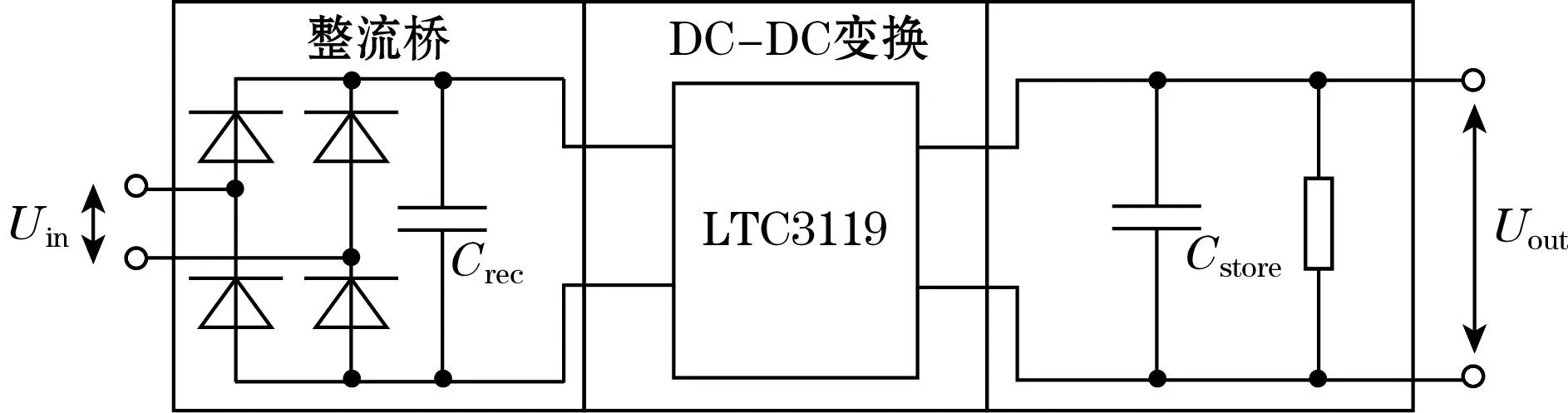
图12 整流降压电路

芯片部分设计通过电阻对LTC3119的输出端进行编程,使电压满足稳定5 V输出,后接有储能元件用于储存电能。同时,LTC3119可以通过编程改变内部电阻从而达到最大功率输出。

3.2 输出功率仿真

搭建COMSOL Multiphysics电磁场仿真,经测试,得到线圈感应电压波形如图13所示,线圈内阻Rcoil=2.56 Ω。

图13 输出功率仿真实验线圈感应电压

将线圈感应电压与内阻作为输入参数搭建电路仿真模型,得到电路消耗的总功率Pcir=208 mW,输出功率Pout=125 mW,略大于目标功率(120 mW),仿真实验较为精确。

4 样机设计与性能实验

4.1 实验场景介绍

基于仿真测试结果,本实验验证输出功率在120 mW时能量收集器的设计方案。

4.2 实验参数的选择确定

实验装置的参数数值设置与表2、表4中保持一致,目标输出功率与仿真实验中相同。实验的输入参数及材料参数如表5所示。

表5 实验输入参数及初始参数

4.3 样机设计

样机设计如图14所示。球形磁铁固定于转子轴上,转子轴放置在轨道中。

(a)转子和轨道组装(b)线圈排布图14 陀螺式旋转能量收集装置样机设计

线圈排布验证实验装置设计如图15所示,对应的线圈排布方案如图11所示。实验所用线圈均为直径0.25 mm的铜导线。

(a)优化前(b)优化后图15 线圈排布验证实验装置图

4.4 线圈感应电压特性验证

启动装置,转子在输入角θ下可以维持稳定旋转,同时,线圈中产生感应电压,实验线圈感应电压波形如图16所示。

图16 线圈感应电压(Ω=127.61 rad/s)

改变输入角速度,可得线圈感应电压与输入角速度的关系曲线,如图17所示。

图17 线圈感应电压与输入角角速度关系

4.5 线圈排布优化效果验证

设计实验以验证线圈排布优化算法及仿真实验的正确性。所用的实验装置如图12所示,所用的转子半径Rmag=0.012 5 m,性能型号N35,剩磁感应强度1170～1210 mT。

经实验测试,得到优化前后线圈排布方案的线圈参数,线圈内阻和输出电压见表6。

实验中,在输出相同目标线圈电压时,使用优化算法后得到的线圈排布方案与优化前相比,线圈匝数减小11.76%,线圈内阻减小26.83%,输出功率提高46.46%,与仿真测试基本吻合,达到预期优化效果。

表6 线圈参数及输出电压

4.6 能量收集器输出功率及效率验证

输出功率及效率验证实验步骤如下：

(2)进一步调节输入角角速度,使输出功率达到当前设计下最大值,维持稳定输出。

实验设计如图18所示。目标输出功率为120 mW,能量收集器的实际最大输出功率为114 mW,输出电压波形如图19所示,能够实现3 V的稳压直流输出。此时转子的稳定旋转角速度为178 rad/s。电路效率为45.60%。实验中受装置精度限制,线圈与转子间隔略大于仿真测试参数,且转子与电路存在机械损耗、铜耗等,损失了一部分效率,使实验电路效率低于相同条件下的仿真测试。

图18 实验装置连接图

图19 能量收集器输出电压

5 结束语

本文研究一种陀螺旋转式振动能量收集器的结构设计与优化。建立了陀螺旋转下机-电理论模型,得到了转子输出功率与转子转速的关系曲线,并通过有限元仿真对球形永磁转子的电磁特性进行分析。提出基于遗传算法的线圈排布算法对线圈结构进行设计优化。在理论模型和线圈排布算法基础上进行系统设计,实现对额定输出功率的最大功率跟踪。搭建振动能量收集平台,加工组装样机进行测试,在1700 r/min的转速下可实现114 mW输出功率。球形永磁转子与圆形线圈绕组的选型设计和线圈结构优化设计在提升稳定性和能量转换效率上有很好的表现,陀螺旋转式能量收集器可以稳定高效率地收集低频振动能量。