基于含水率补偿模型的柔性温度传感器设计
2024-01-23朱良宽徐浩琰孙壮志ArystanRyspayev
白 圆,朱良宽,徐浩琰,孙壮志,付 雪,Arystan Ryspayev
(1.东北林业大学计算机与控制工程学院,黑龙江哈尔滨 150040;2.东北林业大学机电工程学院,黑龙江哈尔滨 150040)
0 引言
植物自身的温度会随着外界环境变化而变化,但是植物温度不一定等于环境温度[1-2]。植物叶片的温度能反映植物的生长状态[3-5]。目前,传统的传感器不能与植物叶片充分接触,所以测量存在一定的误差。柔性可穿戴传感器由于其优异的柔韧性与高灵敏度被运用于植物监测领域。柔性温度传感器可以贴附在植物表面,对环境条件与生长状态实时监测而不会影响植物生长,因此,柔性温度传感器可应用于智能林业监测领域[6]。
在植物监测的应用中,柔性温度传感器通常会受到自身因素和环境的影响。精度补偿在柔性温度传感器的测量中必不可少[7]。许多研究人员都致力于传感器的精度补偿,并提供了解决方法。文献[8]采用恒温温差法可以方便地消除柔性温度传感器的温度漂移。文献[9]基于柔性温度传感器提出了一种新的温度补偿方法。将一个具有类似几何形状且与传感热敏电阻具有相同材料的补偿热敏电阻单片集成到惠斯登桥反馈电路中。当传感热敏电阻和补偿热敏电阻满足几何相似时,温度补偿可以通过电路的反馈控制来自我维持。然而,大多数补偿方法为硬件方法,如搭建电桥式电路,这种补偿方法耗时耗力,调试困难,故近年来软件补偿方法得到了更多的关注[10-11]。
软件补偿方法有插值法、最小二乘多项式曲线拟合法、BP神经网络方法等。插值法[12]是将量程分成多个区间处理,每个区间上用直线去近似代替曲线。然而在实际应用中,效果并不理想。最小二乘多项式曲线拟合法[13]在数据量比较大的情况下,会出现振荡现象,导致无法形成多项式系数。BP神经网络具有很强的非线性映射能力和柔性的网络结构,所以被广泛应用于传感器精度补偿中[14]。尽管BP神经网络具有众多优点,但是由于初始权值和阈值选取的随机性,制约了BP神经网络的性能提升[15]。
另一方面,伴随着群智能算法的快速发展,大量学者通过群智能算法优化神经网路的初始权值和阈值,并取得了很好的效果。刘春艳等[16]采用遗传算法优化BP神经网络的结构,能够在更短的时间内达到更好的效果,数据拟合能力更强。秦琪怡等[17]通过基于粒子群和布谷鸟的方法对BP神经网络实现优化,从减少BP网络对初始权值和阈值的依赖性出发,减缓其陷入局部最优。然而,上述优化算法都存在收敛精度不高、收敛速度不快、求解效率不高等问题。
基于以上分析,本文针对柔性温度传感器的测量精度受含水率影响较大的问题,提出一种带有含水率补偿模型的柔性温度传感器设计方案。首先,基于聚乙烯醇、丙烯酰胺和石墨烯制备了柔性温度传感器。其次,考虑到鹰栖息算法(eagle habitat algorithm,EPO)具有收敛精度高、速度快和求解效率高的优点,提出一种鹰栖息优化(improved eagle habitat optimization,IEPO)BP神经网络模型。再结合标定实验下传感器的测量数据,建立了含水率补偿模型。搭建以单片机为处理器的传感器硬件设备,设计软件驱动程序完成整个补偿功能。最后通过系统测试实验对设计的柔性温度监测系统进行了验证分析,结果表明柔性温度传感器的输出温度接近标定值,可为植物生长环境实时监测提供了一种有效方法。
1 柔性温度传感器的制备
1.1 样品制备
聚乙烯醇水凝胶具有良好的光透射性、化学稳定性和生物相容性。由于其灵活性和延展性仍存在一定的局限性,因此在应用过程中容易断裂,其前景也有一定的局限性。因此,通过将聚乙烯醇和丙烯酰胺在低温下交联,使离子电活性聚合物与聚乙烯醇结合得到了丙烯酰胺水凝胶。它还保留了聚乙烯醇良好的导电性,并由于丙烯酰胺的加入而具有良好的拉伸性。丙烯酰胺水凝胶的离子迁移和偏转对其性能至关重要。内部离子是影响其电导性的重要因素。离子的快速迁移可以通过加入离子电解质来控制,从而影响其电导率。此外,当加入不同的离子电解质时,效果也会有所不同。
制备聚乙烯醇/丙烯酰胺离子电活性聚合物的主要原料包括:聚乙烯醇(分子量为1750±50)、丙烯酰胺(分子量为71.08)、N.N’-亚甲基双丙烯酰胺(分子量为154.17)、N.N.N.N-四甲基乙二胺(分子量为116.21)、过硫酸铵(分子量为228.201)。
具体制备步骤如下:首先,用电子天平称取1 g聚乙烯醇和0.5 g丙烯酰胺。量取25 mL的离子水到烧杯中,加入聚乙烯醇和丙烯酰胺,在85 ℃的环境下水浴加热1 h。接着称取0.1 g石墨烯,加入溶液中继续搅拌30 min。随后称量0.05 g N.N’-亚甲基双丙烯酰胺,2滴N.N.N.N-四甲基乙二胺,0.05 g过硫酸铵加入溶液中,继续搅拌至溶液粘稠。取出烧杯将溶液倒在玻璃板上,并用另一个玻璃板压平压紧。放入-5 ℃低温环境中冷藏12 h,在室温下解冻8 h,等待其内部水融化,最终制得聚乙烯醇/丙烯酰胺离子电活性聚合物,如图1所示。

图1 柔性温度传感器的制备流程
1.2 传感原理
石墨烯是一种由碳原子组成的二维晶体结构,其结构类似于蜂窝状的网络,每个六边形的小单元都由一个碳原子构成,如图2所示。独特的二维结构使它对周围的环境非常敏感,所以石墨烯具有高导电性、高热导性的物理性质,电子在石墨烯中的运动速度达到光速的1/300,优于绝大部分金属[18]。纯的无缺陷的单层石墨烯的导热系数高达5 300 W/(m·K),是导热系数非常高的碳材料,高于单壁碳纳米管(3 500 W/(m·K))和多壁碳纳米管(3 000 W/(m·K))。当它作为载体时,导热系数也可达600 W/(m·K)[19-20]。因丙烯酰胺水凝胶内部含有石墨烯,能对温度变化做出快速响应,所以可以进一步制备柔性温度传感器。随着外界温度不断上升,传感器的阻值也在不断减小,如图3所示。

图2 石墨烯的二维结构

2 IEPO-BP神经网络模型
2.1 BP神经网路
BP神经网络的结构相对简单,但有较强的自学习能力和曲线拟合能力。本文采用BP神经网络进行含水率补偿。在设计BP神经网络的结构时,需要确定输入层、输出层的节点个数和隐含层的层数[21]。本文输入量为电阻和含水率,所以输入层节点数为2。输出量为温度,所以输出层节点数为1。根据标定实验得到不同温度、不同含水量下的实验数据共77组,所以输入样本为77个,输出样本为77个。经验表明,一个单隐含层的BP神经网络就能够满足非线性逼近需求,所以确定隐含层层数为1。根据输入层神经元个数N1与隐含层神经元个数N2的近似关系:N2=2N1+1,设置隐含层神经元个数为5个[21-22]。设计的BP神经网络的结构图如图4所示。BP神经网络的预测结果与各层之间的权重和阈值有关,而这些值的初始值前期都未做处理,都是随机得到的,所以需要采用优化算法进行处理[23]。

图4 BP神经网络的结构图
2.2 鹰栖息优化算法
EPO算法模仿了鹰的栖息行为,具有结构简单、速度快的特点。自然界中每种生物都有自己独特的寻找居住地点的方式。例如,鹰会寻找地形的最高点作为居住点以便捕猎。鹰最终找到的居住点(最高点)即为算法的最优解。鹰栖息优化算法可大致分为2个阶段:鹰在天空中观察整个地形的阶段(探索阶段);重复观察次数,到达地面附近的阶段(勘探阶段)[24]。为了利于EPO算法的寻优,每只鹰的初始位置根据式(1)随机生成。
x=bl+(bu-b1)×rand
(1)
式中:x为鹰的初始位置;bl和bu分别表示寻优的下边界与上边界。
在EPO算法中,由式(2)和式(3)决定算法的搜索范围,具体更新方式如下:
Iscale=Iscale×eta
(2)
(3)
式中:Iscale为表示地形范围的变量,它决定算法由探索阶段到勘探阶段的转变;eta为收缩参数,其取值范围为(0,1);res∈(0,Iscale);T为算法的最大迭代次数。
在EPO算法中,每只鹰的位置更新方式如下:
(4)
Δxi=Iscale×(Ri1,Ri2,…,Rin)
(5)

EPO的算法步骤如下:
步骤1:初始化种群相关参数,具体包括搜索范围变量、收缩变量与迭代次数等;
步骤2:随机初始化种群;
步骤3:计算种群中每只鹰的适应度值,并保留当前最优位置;
步骤4:根据式(2)~式(5)更新种群位置;
步骤5:判断是否满足停止条件,如果满足,则输出最优解,否则,重复步骤3~步骤4。
针对EPO的算法结构可以发现其存在的2个缺点:
(1)与其他群智能优化算法相同,EPO的初始种群是由随机数构成的,所以也存在着全局搜索能力弱的问题。
(2)在高空飞行时,鹰会通过对几个点的取样观察周围,然后向最高点移动,到达最高点后,再次扫视周围,重复同样的过程。因此初始种群至关重要。一旦选择的初始栖息地质量不高,则在后续迭代过程中很容易导致其陷入局部极值,距离最优越来越远。
2.3 改进的鹰栖息优化算法
2.3.1 立方混沌初始化
混沌描述了一种无规律变化的表象下的不确定规则的变动原理[25]。在标准EPO算法中,鹰栖息的初始位置是随机分布,位置分布不均匀。因此引入混沌序列初始化种群,提高种群中解的质量。目前常用的混沌优化方法有Logistics映射[26]、Cubic映射[27]等。根据图5的混沌分布图,本文选择分布更均匀的Cubic映射(立方混沌映射)生成混沌序列,从而获得分布更加均匀的种群。Cubic映射定义如下:
(6)
式中:xn∈(0,1);β为控制参数,β=2.595。
2.3.2 精英反向学习初始化
反向学习策略(opposition-based learning,OBL)由学者Tizhoosh根据现实世界中事物之间的对立关系提出。在种群初始化中引入该策略可以有效提高初始解的质量,使生成的初始解更贴近全局最优的区域,从而提高算法的收敛效率。随着研究的深入,针对反向学习策略存在的反向解不一定优于当前解的问题,在实际应用中得到改进,精英反向学习策略(elite opposite based learning,EOBL)是在反向学习策略的基础上根据当前种群的适应度值选出精英个体[28]。

(a)逻辑映射

(b)立方映射图5 混沌分布图
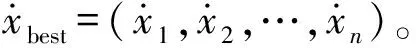
(7)
(8)
(9)
式中:xi∈[ai,bi];k∈[0,1],由于k是随机的,生成的反向种群也是随机的,因此可以在一定程度上提高算法的勘探能力;[dai,dbi]为种群在第i维的动态区间,dai为上界,dbi为下界。
当精英反向解的取值超出区间范围时,需要对越界值重置,重置的方式如式(10)所示。
(10)
动态边界的优点在于可以充分利用算法前期的搜索经验,并在迭代的过程中逐步缩小反向解的范围,使算法更快地搜索到最优解。
2.3.3 混沌精英反向学习初始化
由于精英反向学习策略中的k是随机的,生成的反向种群也是随机的,因此,可以将立方混沌优化方法与精英反向学习策略结合,使种群初始化生成高质量的初始解。具体的改进鹰栖息优化算法的BP神经网络流程如图6所示。

图6 改进鹰栖息优化算法的神经网络流程图
3 基于含水率补偿的温度检测模型分析
3.1 实验数据的获取与分析
对柔性温度传感器进行二维标定实验,定性得出含水率对传感器的测量精度有影响。具体操作流程:首先确定一个温度标定点,在该标定点下不断调整含水率,分别得出柔性温度传感器的输出电阻。通过实验分析得出结果:由于传感器的含水率不同,即使在相同温度标定点下,柔性温度传感器的输出电阻也不相同,含水率影响传感器的电学性能。本文选取0.35、0.40、0.45、0.50、0.55、0.60、0.65作为7个含水率标定点,其中0.35是指面积为0.35 cm×0.35 cm的传感器薄片。选取的温度区间为30~80 ℃,分成11个温度测量点,分别为30、35、40、45、50、55、60、65、70、75、80 ℃。二维标定实验得到的测量数据如图7所示。

图7 柔性温度传感器二维标定实验数据
从图7可以看出,在含水率补偿前柔性温度传感器的输入输出受到含水率影响很大,即当自身含水率变化时,输出电阻会产生一定范围的漂移。
为了更好地分析含水率对测量精度的影响,需要进行定量计算。本文采用常温含水率系数∂c、灵敏度含水率系数∂T、含水率附加误差∂H3个静态特性参数。∂c表示常温时电阻随自身含水率变化的速度大小,∂T表示灵敏度随自身含水率变化的速度大小,∂H表示因测量含水率偏离标定而带来的偏移百分比,其数学表达分别如式(11)~式(13)所示。

(11)

(12)
(13)
式中:ΔRcm为常温时,不同含水率导致的电阻最大漂移值,ΔRcm=Rc(H2)-Rc(H1);ΔH为柔性温度传感器自身含水率的变化量;R(FS)为本实验中电阻勘测范围变化量;|ΔRm|为在某一特定的温度T条件下,由含水率变化导致电阻产生的最大偏移量,|ΔRm|=|R(H2)-R(H1)|。
由于∂c=3.08,∂T=3.33,∂H=99.80%,柔性温度传感器存在很大的改进空间,因此可以对其进行含水率补偿。
3.2 含水率补偿建模及结果分析
在含水率标定实验中,将含水率、温度以及柔性温度传感器的输出值共3组数值分别进行BP、EPO-BP、IEPO-BP 3种补偿模型处理。通过二维标定实验,一共得到77组数据。按照5:2的比例,随机选择55组数据作为神经网络的训练集,22组数据作为神经网络的测试集。分别使用BP、EPO-BP、IEPO-BP 3种补偿模型训练实验数据,最终得出柔性温度传感器在含水率补偿后的输入输出特性曲线,如图8所示。

(a)BP模型

(b)EPO-BP模型

(c)IEPO-BP模型图8 含水率补偿后的柔性温度传感器输入输出特性曲线
从图8可以看出,分别使用BP、EPO-BP、IEPO-BP 3种补偿模型补偿后,柔性温度传感器测得的温度误差明显减小,有效地提高了测量结果的准确度,满足了实际应用要求。
为了定量比较EPO-BP、IEPO-BP 2种补偿模型和一般BP补偿模型的异同,将3种模型的相关指标和模型下传感器的静态特性参数分别做了计算比较研究。对于相关指标的计算,具体表达如式(14)~式(16)所示。
(14)
(15)
(16)
式中:R2为决定系数;ESS为可解释的变化;TSS为总变化;RSS为无法解释的变化;MAE为平均绝对误差;predictedi为预测值;actuali为真实值;MBE为平均相对误差。
R2越大,表示自变量对因变量的解释程度越高,自变量引起的变动占总变动的百分比高,观察点在回归直线附近越密集[29]。
通过采用基于BP、EPO-BP、IEPO-BP算法建立的模型,对实验所得样本数据进行训练,然后对训练的结果进行测试,计算得到的3个补偿模型的相关指标,如表1所示。从表1可知,决定系数R2:IEPO-BP>EPO-BP>BP;平均绝对误差MAE:BP>EPO-BP>IEPO-BP;平均相对误差MBE:BP>EPO-BP>IEPO-BP。综合评价可得,IEPO-BP含水率补偿模型的相关指标最佳。

表1 3种模型的相关指标计算
对于含水率补偿后的输出值,计算∂c、∂T、∂H,如表2所示。与式(11)~式(13)进行对比,得到如下的结果:各模型相比补偿之前都得到了改善,含水率对输出的影响显著降低,从而提高了系统的测量精度。其中IEPO-BP模型的补偿效果最好,最终选用IEPO-BP模型作为含水率补偿模型。
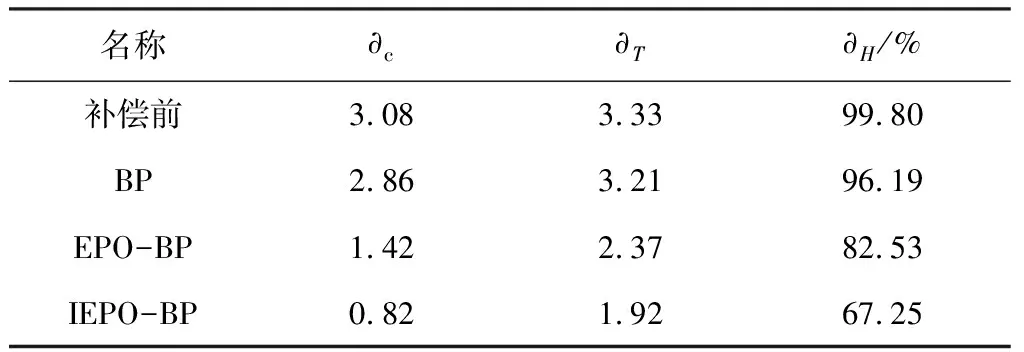
表2 静态特性参数
4 柔性温度传感器的设计
4.1 柔性温度传感器硬软件设计
为了能对温度进行实时高精度的测量,需要对柔性温度传感器搭建测量系统。系统硬件部分主要包括STM32F405RGT6芯片、A/D转换、串口通信、信号调理电路、放大电路和低通滤波等模块。系统的硬件设计总体框图如图9所示。柔性温度传感器测量系统选用STM32F405RGT6单片机,其作用是:将训练好的IEPO-BP算法固化在此单片机中,然后通过此算法对A/D转换模块输出的数字温度电压信号和采集模块获取的数字信号进行数据融合,得到含水率补偿后的预测温度值[30]。STM32F405RGT6引脚图如图10所示。模拟温度监测系统主界面是系统各个子模块切换的核心。模拟温度监测系统主界面主要包括温度报警模块、温度数据显示模块和数据存储模块,如图11所示。根据系统的硬件设计总体框图要求,将所需要用到的芯片模块集成到PCB实验板上。对实验板进行测试调试,确保功能正常后,接入柔性温度传感器。通过VISA,实现下位机和上位机LabVIEW之间的通信。同时通过MATLAB,完成含水率补偿。搭建的测试环境如图12所示。
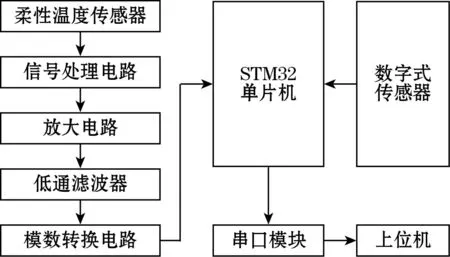
图9 系统的硬件设计总体框图

图10 STM32F405RGT6引脚图

图11 模拟温度监测系统主界面图

图12 搭建的测试环境
4.2 系统测试结果
为了保证柔性温度传感器测量系统正常运行,先对下位机和上位机之间进行测试,确保功能正常后,再接入柔性温度传感器。运行测量系统,输出在不同含水率条件下的温度测量结果到显示界面,如图13所示。将测试结果与标定值进行比较,分析系统性能的优劣。本文选择0.30、0.36、0.42和0.48标定含水率条件下的30、36、42、48、54 ℃温度测量点进行系统性能验证,测试结果如图14所示。从样本组队列表中选取不同含水率下的标准值和与其对应条件下的测量值做减法,就得到了测量误差的数值。同时将这些运算得到的测量误差数值和与之对应的含水率值进行取点绘图,结果如图15所示。由图15可以看出,在含水率为0.30、0.36、0.42和0.48的条件下,平均测量误差分别为0.56、0.70、0.53和0.68。测试实验结果表明含水率补偿算法较显著地降低了柔性温度传感器的测量误差,验证了本文所提方法的可行性。
5 结束语
本文提出一种带有含水率补偿模型的柔性温度传感器设计方案。以石墨烯为导热填料,以聚乙烯醇和丙烯酰胺为基体制备了柔性温度传感器,并讨论了柔性温度传感器的传感原理;针对含水率对测量精度的影响问题,采用改进的鹰栖息算法优化BP神经网络建立了柔性温度传感器的含水率补偿模型,使得常温含水率系数从3.08下降到0.82、灵敏度含水率系数从3.33下降到1.92、含水率附加误差从99.80%下降到67.25%。通过STM32和LabVIEW构建了一套完整的测量系统,系统测试结果表明:在含水率为0.30、0.36、0.42和0.48的条件下,平均测量误差分别为0.56、0.70、0.53和0.68,测试的输出结果都很接近温度的标定值,实现了提高测量精度的目的,使得对植物生长环境测温工作更加便捷、有效。

图13 系统显示界面

图14 不同含水率条件下的温度测量值

图15 不同含水率条件下的温度测量误差
