义务教育阶段学生数据观念发展水平评价框架建构

2024-01-22沈尚

中学数学杂志(初中版) 2023年6期

【摘要】 “数据观念”是《义务教育数学课程标准（2022版）》核心素养之一，是义务教育阶段统计与概率的核心目标.此次课程标准的发布，对统计与概率领域做出诸多调整，评价学生的数据观念发展水平是数学课程与教学的重要任务.通过对数据观念内涵及行为表现的分析，借鉴已有相关研究成果，构建义务教育阶段学生数据观念发展水平评价框架，分为4个维度，每个维度分为由低到高4个水平.

【关键词】发展水平；数据观念；评价框架

1 引言

当代社会，数据素养成为新时代公民的必备素养.数据素养是具备数据意识和数据敏感性，能够有效且恰当地获取、分析、处理、利用和展现数据，并对数据具有批判性思维的能力［1］.“统计与概率”是培养学生数据素养的最主要知识载体，“统计与概率”领域于2001年正式进入中小学课程，历经多次调整，逐步成为数学课程的重要组成部分.《义务教育数学课程标准（2022年版）》（以下简称《课标2022》）面向未来，聚焦核心素养，核心素养具有高度的整体性、一致性和发展阶段性，在不同学段有不同的表现，将“数据意识”“数据观念”分别作为小学、初中阶段数学核心素养之一［2］，这一阶梯式的培养目标更符合学生发展规律.

《课标2022》已进入实施阶段，新教材未落地，我们需要对当前学生数据观念有具体的认识，以便了解教育教学与《课标2022》相关要求的差距.只有准确了解学生数据观念发展水平，教师才能确定有效的教学目标，选择合适的教学策略.这就需要建立学生数据观念发展水平评价框架，以便对学生数据观念进行评价.《课标2022》虽提出“内容要求”和“学业质量标准”，但无具体评价框架，因此，研究者通过对“数据观念”内涵及行为表现的分析和已有相关研究成果的借鉴，尝试构建数据观念发展水平评价框架.2 数据观念的内涵

2.1 观念

在心理学中，广义的观念是一切心理反映形式的总称，狭义的观念和表象同义，包括由知觉而来的感性形象的再现和由原初形象组合而成的新的观念整体［3］.《辞海》中观念解释为：“思维活动的结果”“有时候亦指客观事物在人脑中留下的概括形象.”史宁中教授将观念解释为“意识的高级阶段”，认为观念是经历一定过程后基于意识与能力上而形成的某种认识［4］.由此可见，观念是基于概念，通过认知和实践活动，建立在意识和能力基础上对客观事物的总体的、综合性的认识.

2.2 数据观念

《课标2022》将数据观念内涵界定为：“数据观念主要是指对数据的意义和随机性有比较清晰的认识.知道数据蕴含的信息，需要根据问题的背景和所要研究的问题确定数据收集、整理和分析的方法；知道可以用定量的方法描述随机现象的变化趋势及随机事件发生的可能性大小.形成数据观念有助于理解和表达生活中随机现象发生的规律，感知大数据时代数据分析的重要性，养成重证据、讲道理的科学态度［2］10.”这一表述，相对于《义务教育数学课程标准（2011年版）》中核心概念“数据分析观念”，舍去“分析”二字，内涵增大，“数据观念”上位于“数据分析观念”.该内涵的表述就具体行为表现来看，涵盖四个方面：一是对数据的意义和随机性的感悟与认知.学生要能亲身经历数据收集的过程，知道根据不同的问题需要收集不同的数据，同样的问题可以收集不同的数据［5］；感悟数据的实际意义，知道数据具有多样性；感悟样本数据的意义和随机性，体会抽样的必要性，感悟数据的变异性［5］4.二是对数据整理、描述与分析方法的感悟与理解.学生会对数据进行分类，能根据問题的需要绘制不同种统计图表整理与描述收集到的数据，选择合适的方法进行分析，理解统计量的意义，能根据问题的需要提取、计算统计量并科学推断；知道样本与总体的关系，感悟通过样本特征估计总体特征的思想.三是对现实随机事件的概率的意义的感悟与描述，感知随机现象，感悟概率的意义与基本特征，能用定量的方式描述随机现象的变化趋势及随机事件发生可能性的大小，理解频率的稳定性，能用频率估计概率，感悟数据的随机性、概率与统计的关系［6］.四是对统计解决问题的特点、过程与意义的理解与创新［5］6，在真实情境中形成统计问题，有效收集数据，恰当分析数据，合理解释结果，从而去理解数据、统计量的意义和数据处理的基本方法，感知大数据时代数据分析的重要性，学会用数据“说话”，能在真实情境中充分挖掘数据条件，运用统计与概率的知识解决问题并进行科学推断、预测，养成重证据、讲道理的科学态度.

“数据观念”内涵及课程内容要求呈现以下变化特点：一是与时俱进，面向未来，体现时代性.数据分析应用于社会的各个层面，社会的飞速进步对个人的数据素养提出新的要求.内涵的表述首次在义务教育阶段明确提出“感知大数据时代数据分析的重要性”，在课程内容上增加“四分位数、箱线图”，感受大数据时代分布式计算［2］74，面向未来，与时俱进，体现时代性.二是承前启后，注重衔接，体现关联性，《课标2022》舍弃所有学段核心概念统一表述的形式，提出核心素养的总体目标，分学段采用“数据意识”“数据观念”“数据分析”的不同的表述，体现素养形成的过程性、持续性特点［7］.数据意识更强调在面对具体问题的时候，依据数据蕴含信息与规律作出判断和决策的习惯性心理倾向.意识是基于经验的感悟，数据意识是数据观念的基础，数据观念是数据意识发展的新阶段，观念是基于概念理解的，是整体、综合性的心理倾向；数据观念是数据分析的关键，数据分析更关注模型与应用，模型与应用意识需从观念萌发.数据观念作为初中阶段核心素养之一，衔接小高，承前启后.三是注重感悟，关注推断、预测，体现应用性，《课标2022》强调在现实情境中感悟统计量的意义；关注学生推断能力的培养，强调学生经历样本推断总体的过程，体会抽样的便利性和合理性；强调用定量的方法描述随机现象的变化趋势［2］73；注重数据的处理方法，强调学生收集、整理、分析数据的基本方法，能根据具体情境问题的需要选择合适的方法，强调通过真实、有意义的统计活动帮助学生形成初步的知识体系，从而领悟数学的思想方法［2］76；强调跨学科进行项目学习，尝试使用计算机进行处理数据，体现应用性［2］77.四是关注过程，注重结构，体现方向性，《课标2022》对“统计与概率”领域结构进行了优化，初中阶段主题未作调整，关注侧重点从能力向素养转变，从虚拟情境到真实情境转变，从关注统计结果向关注统计过程转变，强调对统计整个过程的感悟与结构化认知，为高中阶段数据分析的培养指明方向.

3 数据观念评价框架研究现状

国外统计与概率领域评价更多关注统计思维，基于SOLO分类理论.国内更多基于“数据分析观念”内涵进行评价，代表性的主要有两类：一是关注数据分析内涵的认知模型，重点关注内隐的认知过程，如童莉［8］借鉴SOLO分类理论进行水平划分，认为观念是一种认识和感悟，将数据分析观念划分为三个维度，分别是对数据、数据分析方式、生活中随机现象的意识及感悟，每个维度划分3—4个水平；二是关注数据分析观念的外在表现和内隐过程的综合模型，张丹［9］将数据分析观念的评价框架划分为3个维度9个要素，各要素又划分四个水平，较为系统地考察了小学生在教学情境下数据分析观念的发展阶段水平表现.关于“数据观念”评价框架主要有以下：张晨琛［10］基于SOLO分类理论，在童丽莉、张丹的基础上进行调整；喻平［7］126基于知识学习，分析布鲁姆、PISA模型和SOLO模型各自的优缺点和《课标2022》中数学核心素养“内涵”与表现的描述，提出关键能力划分水平，将核心素养划分为水平1（知识理解）、水平2（知识迁移）、水平3（知识创新）三级水平.其中有关数据观念（初中）的划分为：水平1为知道数据蕴含着信息，需要根据问题的背景和所有要研究的问题确定数据收集方法，水平2理解随机现象，掌握数据的整理和分析的基本方法，水平3能够选用恰当方法构建统计模型并能够对其进行数据处理［7］127.刘雪［11］从分析数据观念内涵入手，依据布鲁姆的教学目标分类理论，同时综合参考喻平教授对数学核心素养水平的划分及童莉教授对义务教育阶段学生数据分析观念水平的划分，将初中生统计与概率学习划为“对数据意义的认识”“对数据收集、整理和分析方法的认识”“对数据随机性的认识”三个维度，每个维度分为四个水平.

以上关于数据分析观念或数据观念水平评价框架被教育界广大学者认可，框架建立的出发点都认为思维、意识、观念不易直接测量和评价，但可以划分水平，可以通过检测现实知识的过程中分析学生的思维、观念的水平.所以，研究者借鉴以上评价框架，参照《课标2022》中学业质量标准、数据观念内涵及外在行为表现，尝试构建初中学生数据观念发展水平评价框架.4 数据观念发展水平评价框架的构建

《课标2022》首次提出学业质量标准，学业质量标准是学生在完成课程阶段性学习后的学业成就表现，反映核心素养的要求，学业质量标准是以核心素养为主要维度，结合课程内容，对学生学业成就具体表现特征的整体刻画［2］80-81.提出从“结构化的知识与技能”“情境化的解决问题”“良好数学品格”三个方面评估学生核心素养，本质上是三个层次水平.基于此点，从“统计与概率”教学内容出发，参考专家学者对数据观念的行为表现的解读，基于《课标2022》对“数据观念”内涵的阐释，关注数据处理过程中统计思维发展水平，将义务教育阶段学生数据观念发展水平评价设为4个维度：一是对数据的感悟，对数据收集的认知与感悟；二是对数据的整理、描述、分析和解释的理解与迁移；三是对现实现象随机性的感悟与描述；四是对统计解决问题的特点、过程与意义的理解与创新.每个维度划分4个水平层次，水平0：不具备数据观念；水平1：零散数据观念；水平2：片面数据观念；水平3：完备数据观念.

4.1 维度一：对数据的感悟，对数据收集的认知与感悟

维度一主要强调学生是否知道数据蕴含信息，对数据的随机性和变异性是否有清晰的认识；是否能根据问题的需要选择合适的数据收集方式，能否设计恰当的调查问卷并会用简单随机抽样的方法收集数据.以此维度划分为四个水平，见表1［12］.

维度的水平评价，可以采用测试题访谈、问卷访谈或项目过程评价的方法.现就测试题访谈做举例说明，编制测试题，通过结构性访谈，根据学生对问题的看法和解答，对学生的维度水平进行評价.

测试样题1：如果想在学校附近开家奶茶店，主要经营四种口味的奶茶，消费主体是本校的学生.奶茶原料不易存储，如果你是奶茶店的老板，你怎样确定每天四种口味奶茶的原料各准备多少？请写出你解决问题的具体过程和详细步骤.

分析：此问题数据特征不是很明显，对于此问题，学生若不知道怎样回答，或是凭借自己的感觉回答准备多少，则表明学生处于水平0，若学生意识到去调查有多少学生有意愿去购买奶茶，每种口味的有多少人，没有具体的调查思路，说明学生处于水平1；如果学生能够意识到设计调查问卷，调查学生的购买意愿、口味选择等数据，并指出具体的调查方法，说明学生处于水平2；在水平2的基础上，学生能意识到调查学校附近其他的奶茶店、学校附近食品相关行业的消费群体数量、销量等数据进行综合分析，并提出具体的调查方法，说明学生意识到从不同渠道、角度收集数据进行综合判断，则说明学生处于水平3.

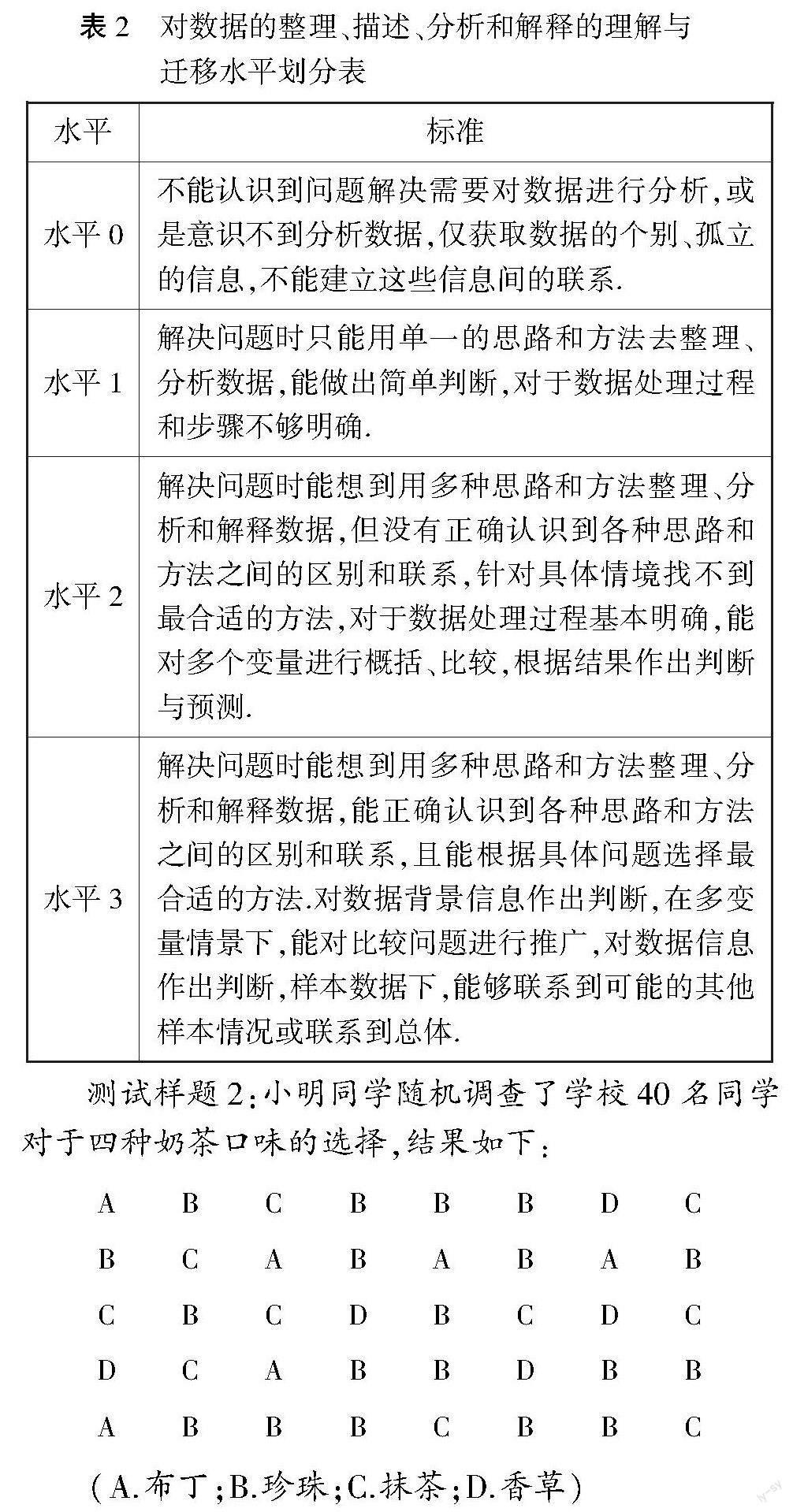
4.2 维度二：对数据的整理、描述、分析和解释的理解与迁移

维度二是数据观念形成的核心，强调学生是否能够读懂、制作各种统计图表；能否计算各种统计量，对数据的分布有初步的认识；理解样本与总体的关系，是否能根据数据的数字特征进行合理的解释问题，进行判断和预测.重点是对同样的数据采用多种分析方法，根据问题和情境的需要选择合适的分析方法进行数据分析，感悟样本特征估计总体特征的思想.此维度划分为四个水平，见表2［13］.

测试样题2：

小明同学随机调查了学校40名同学对于四种奶茶口味的选择，结果如下：

ABCBBBDC

BCABABAB

CBCDBCDC

DCABBDBB

ABBBCBBC

（A.布丁；B.珍珠；C.抹茶；D.香草）

根据上述信息，你能得出哪些结论？你是奶茶店的老板，你会做出怎样的决定？请写出你的分析过程及相应结论.

分析：测试题2改编自苏科版八上第7章《数据的收集整理描述》，主要考查学生对数据处理过程的了解，是否能够制作相关统计表格有效描述数据，根据分析结果做简单的解释和推断.此题考查了整理数据、描述数据、分析数据、决策完整过程，考查内容全面、合理，属于综合型主观题，学生的解答过程能够较真实地反映出学生对数据分析方法的掌握情况.若学生没有作答或作答缺乏理性思考，没有逻辑关联，则表明学生在此维度处于水平0；若学生直接得出一些结论或是只采用了单一数据分析方法，比如统计A的频数没有做出相应的决策，表明学生处于水平1；若学生采用了多种数据分析方法，比如制作条形、扇形统计图等进行数据分析，计算频率，但各种方法之间没有建立本质的沟通，对于为什么选择这样的分析方法较为模糊，对结论的解释不够明确，决策不明确，表明学生处于水平2；在水平2的基础上，学生能够制作频率分布直方图、扇形统计图等分析整理数据，对结果的解释得很详细，决策明确，表明学生处于水平3.

测试样题3［2］164：现有A和B两个奶茶公司可以加盟，它们负责加盟店的原料、技术、营销.2018—2020年，这两个连锁加盟公司负责经营相同的12项加盟产品，加盟店各项加盟产品收益率（%）如下：

A：4.77 3.98 6.44 4.89 2.15 3.85

3.64 3.21 3.18 2.02 4.11 4.10

B：3.18 3.84 3.99 3.67 3.40 3.60

4.10 4.21 4.15 4.44 3.87 3.91

若只能选择一家公司加盟，并经营全部产品，你会做出如何选择？

分析：这一问题源自《课标2022》例87，问题考查对统计量意义的理解，侧重于数据分布，强调多种方法对数据进行分析，注重根据问题的需要选择合适的方法进行分析、解释和决策.若学生没有数据分析，直接选择，则学生处于水平0；若学生能够制作单一统计图或是计算统计量，作出决策，说明学生处于水平1；若学生通过计算平均数、中位数、方差等进行比较分析，但不能在统计量间进行转化，对于什么情况下选择什么数据分析的方法不清晰，则学生数据观念处于水平2；若学生计算平均数、方差、四分位数，制作数据分布图进行分析，并对决策推断做出合理解释，说明学生处于水平3.

4.3 维度三：对现实现象随机性的感悟与描述

该维度侧重于对随机现象的感知，感悟概率的意义；描述简单随机事件的特征；体会频率与概率间的关系；意识到同样的事情不同的收集方法每次收集的数据可能不同，但是当数据足够多时可能从中发现规律，此维度划分为四个水平，见表3［8］47.

分析：此题主要考查学生能否用表格、树状图等方法刻画简单随机事件所有可能性的结果以及指定随机事件发生的所有等可能结果.若学生直接作答，没有图表及计算过程，则学生处于水平0；若学生意识到用图表进行分析，但分析过程错误或是结果错误，则学生处于水平1；若学生能够通过图表列出所有等可能性结果，并定量描述比较，则学生处于水平2；若学生能够通过图表列出所有等可能性结果、指定随机事件的所有结果，通过计算进行定量描述，则学生处于水平3.

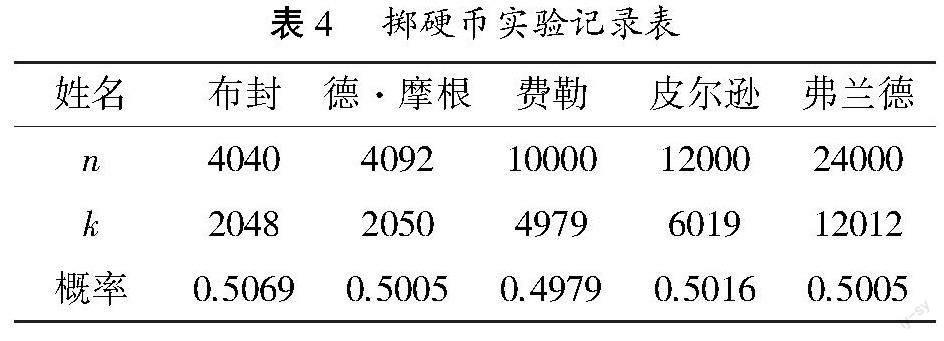
测试样题5［15］：表4是Coin flipping or coin tossing（掷硬币实验）记录：投掷次数n，其中正面出现次数k，正面出现的频率k/n．参考下表的数据，请估计硬币出现正面的概率为，为什么？表4 掷硬币实验记录表

姓名布封德·摩根费勒皮尔逊弗兰德

n40404092100001200024000

k204820504979601912012

概率0.50690.50050.49790.50160.5005 分析：此题主要考查学生对于数据的随机性、概率与概率关系的认知.若学生没有作答或是错误，则学生处于水平0；若作答0.5，仅从抛掷硬币两种结果去解释，或是基于经验，没有从频率的大量数据中去寻求频率的规律，则学生处于水平1；若作答0.5，能理解正面朝上的频率是不同的，寻找频率在大量数据中的规律，并推测结果，但没有把频率与概率明确分开，解释频率与概率关系较为混乱，对这两个概念没有形成正确认识［8］47，则学生处于水平2；能从频率的数据中发现规律，认识到在相同条件下大量重复实验，随机事件发生频率具有稳定性，可以用频率估算随机事件发生的概率，认识到硬币的出现正面的概率是一个确定的值0.5，说明学生处于水平3.

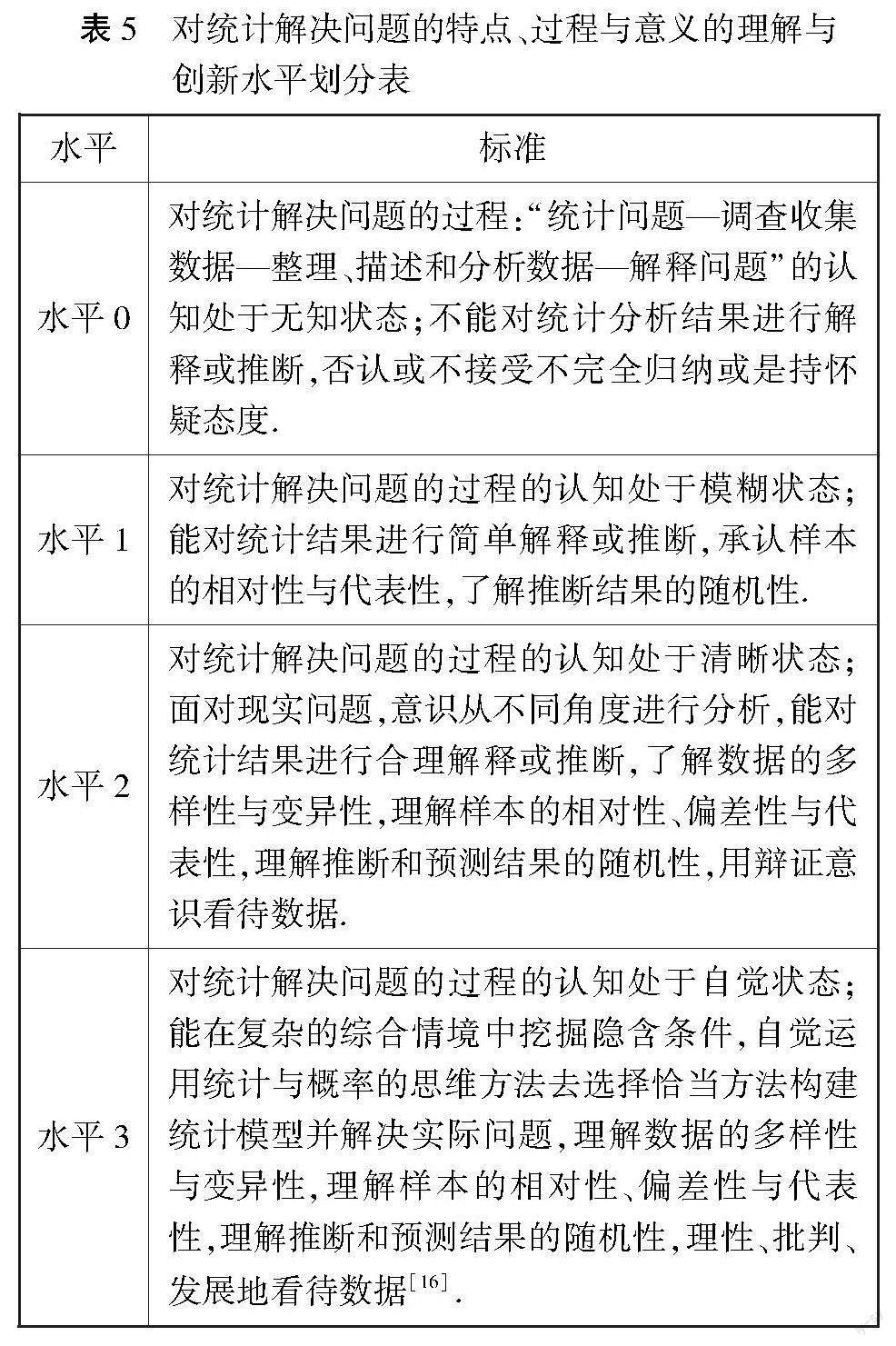
4.4 维度四：对统计解决问题的特点、过程与意义的理解与创新

统计作为一级学科，其基本研究对象及思想方法与确定性数学在立论基础、推理方法和判断原则上有较大差异［5］10.学生是否对统计解决问题的过程和方法有清晰的认识是数据观念形成的关键.该维度更多关注的是学生对统计的推理方法和判断原则的认知与理解，是学生在学习统计与概率后应形成的思维模式和数学品格.

此维度强调对统计与概率的结构化认知，从单个问题无法反馈学生的认知与理解水平，适合问卷调查或项目问题解决的过程观察，在此不做水平划分举例.

以上，建立了数据观念的初步评价框架，从定性的角度对义务教育阶段学生数据观念做出评价.因研究者理论水平有限，该框架是否能真正刻画义务教育阶段学生的数据观念，还需要在实践中进行定量分析和完善.参考文献［1］郝媛玲，沈婷婷．数据素养及其培养机制的构建与策略思考［J］.情报理论与实践，2016：58-63.

［2］中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022：9-10.

［3］费金有.中学物理教师课程价值观念的透视与反思［D］.长春：东北师范大学，2010：13.

［4］史宁中，张丹，赵迪.“数据分析观念”的内涵及教学建议——数学教育热点问题系列访谈之五［J］.课程·教材·教法，2008（06）：40-44.

［5］鲍建生，章建跃.数学核心素养在初中阶段的主要表现之六：数据观念［J］.中国数学教育，2022（21）：3-11+21.

［6］栾长伟.新课标初中数学“统计与概率”部分的主要变化与教学实施策略［J］.辽宁教育，2022（21）：17-21.

［7］喻平.《义务教育数学课程标准（2022年版）》学业质量解读及教学思考［J］.课程·教材·教法，2023，43（01）：123-130

［8］童莉，张号，张宁.义务教育阶段学生数据分析观念的评价框架建构［J］.数学教育学报，2014，23（02）：45-48.

［9］张丹.小学生数据分析观念发展过程的研究［D］.长春：东北师范大学，2015：185.

［10］张晨琛.初中“数据观念”培养现状调查及对策研究［D］.杭州：杭州师范大学，2022（12）：14-15.

［11］刘雪.基于数据观念的初中统计与概率教学现状研究［D］.新疆：昌吉学院，2023（05）：17.

［12］朱琰.初中生数据分析观念发展水平的调查与研究［D］.天津：天津师范大学，2019：14.

［13］李红云，朱文芳，伍春兰.学生统计思维发展水平划分探究［J］.数学教育学报，2019，28（05）：41-46.