基于模型种群分析变量选择的红外光谱建模方法
2024-01-21郭鲁钰徐啟蕾单宝明张方坤
杜 康,郭鲁钰,徐啟蕾,单宝明,张方坤
(青岛科技大学自动化与电子工程学院,山东 青岛 266061)
0 引 言
在工业工程中,变量选择对于各种过程分析仪校准模型的建立至关重要,它决定了所建模型的准确性、可靠性、可解释性和鲁棒性[1-3]。随着光电技术和传感器技术的发展,光谱技术已经成为获取物质定性和定量信息的重要手段[4-5]。一条光谱由成百上千的变量组成,其包含样品特性、环境、光纤和仪器等丰富信息,也包含很多不相关的变量和噪声等[6-7]。若对变量及噪声进行不合理的选择和处理,将严重影响模型的可靠性和准确性[8]。事实证明,通过变量选择在提高标定模型准确性和可靠性上具有明显的效果和优势[9],因此,在过去的几年中,对变量选择方法的研究得到了普遍关注和重视[10-13]。
近年来,基于模型群体分析(Model Population Analysis,MPA)策略的变量选择方法在光谱数据建模中表现出卓越的性能[1]。许多优秀变量选择方法得到进一步发展,如竞争性自适应重加权采样法[14]、变量组合总体分析(Variable Combination Population Analysis,VCPA)法[15]、自举软收缩(Bootstrapping Soft Shrinkage,BOSS)法[16]、迭代缩减窗口自助软收缩法[17]和显著多变量竞争群体分析法[18]等。MPA的核心思想是通过随机抽样产生大量的子集,并对子集进行建模和分析,来评价变量的优劣[19]。然而,由于每个子集都需要重新建立一个偏最小二乘(Partial Least Squares,PLS)模型,因此,该方法相对比较耗时。其中,BOSS 和VCPA 变量选择方法[15-16],均采用NIPALS 算法进行PLS 建模,NIPALS 需要对数据矩阵进行缩放,并计算2 组加载向量,这加剧了模型迭代时间和计算机内存消耗[20]。尤其,当数据量比较大时,这种劣势将特别明显。目前,基于MPA 技术开发的变量选择方法还存在建模效率和稳定性差的问题[21],如何提升建模效率和可靠性值得进一步研究。近年来,众多改进的PLS 算法被提出[22],Bjorck 等[23]将6 种改进的PLS 算法与NIPALS 算法进行了数值精度和计算效率的比较。结果表明改进的PLS 算法可以有效提升建模速度但会降低模型精度。然而,通过索引技术避免子模型重复计算来提升基于MPA 策略的变量选择方法,从而提升模型精度和效率的方法还未见报道。
为解决上述问题,本文将分别从变量和样本2 个角度,将PLS建模方法和索引技术与变量选择方法进行结合,提出一种基于子集索引重用核-PLS(Subset Index Reuse Kernel-Partial Least Squares,SIRKPLS)的融合建模方法。该方法根据数据集的样本数和变量数自适应实现对建模方法的自动切换。最后,通过在玉米数据集上与各种典型的建模算法进行比较,对所提融合建模算法的有效性进行验证。
1 基本原理
1.1 变量SIRK-PLS算法
当数据集的样本数远远大于变量数(m≫n)时,Lindgren 等[24]提出了一种核PLS 算法,其利用小的核矩阵和与其关联的协方差矩阵(XTXn×n)来计算PLS 模型的回归系数。结合MPA 的原理,本文提出变量SIRK-PLS(Variable SIRK-PLS,VSIRK-PLS)算法。
设X=[x1,x2,…,xn],则:
由式(1)可知,X中的任意变量xi,仅为XTXn×n中第i行和第i列提供信息。在MPA 变量选择过程中,对于不同子集的PLS 建模,VSIRK-PLS 算法只需计算一次协方差矩阵XTXn×n,利用变量的索引便可从XTXn×n中提取出任意子集的协方差矩阵,最后利用核PLS算法建立PLS子模型。
为了解释和阐明VSIRK-PLS 算法的基本原理,考虑以下示例:假设随机抽样得到的某一变量子集包含第i行和第j列的变量,提取XTXn×n中的第i行和第j列相交的元素,即为该子集的协方差,最终通过子集的协方差便可建立PLS 子模型。对于变量选择中每次重复执行PLS 计算,VSIRK-PLS 算法通过计算n×n的核矩阵与协方差核来减少数据的储存量,通过变量索引技术减少重复计算量,建模效率有显著提升。
1.2 样本SIRK-PLS算法
当数据集中的变量数远远大于样本数(n≫m)时,XTXn×n将变得庞大,继续通过XTXn×n来估计PLS回归系数将加大运算负担。针对这一问题,Rannar等[25]提出了通过计算小的核矩阵(XXT)与协方差矩阵()来估计PLS 回归系数的核PLS算法。由于中不再独立包含某个变量的完整信息,因此无法通过对索引,建立PLS子模型。但是中完整包含了m个样本的信息。考虑到PLS算法在计算回归系数前,需要将样本划分为k折,建立k个PLS 模型进行交叉验证来评估最优因子数,因此本文提出样本SIRK-PLS(Sample SIRKPLS,SSIRK-PLS)算法。
SSIRK-PLS 算法只需计算一次,通过索引中对应的行和列,即可得到任意折样本对应的协方差,从而可通过协方差估计出该折样本的PLS 回归系数。SSIRK-PLS 算法通过对交叉验证所划分建模样本的索引,实现对矩阵的重用,提高了最优因子数求解的效率。
1.3 SIRK-PLS建模方法
由于上述2 种算法适用于不同尺寸的数据集,并且在变量选择过程中随着无关变量的剔除,数据集尺寸随之变化。为了保证在任意尺寸数据集上及变量选择迭代过程中,算法均能高效运行,本文提出SIRK-PLS建模方法。
定义ε来衡量数据集尺寸:
式中:m为样本数,n为变量数。图1 所示为SIRKPLS 融合MPA 变量选择的建模算法。基于MPA 的变量选择方法主要包括随机抽样程序、子模型建立程序和统计分析程序。将SIRK-PLS 建模方法用于子模型建立程序。当ε<0.4时,SIRK-PLS建模方法自动选择SSIRK-PLS 算法建立子模型;随着变量选择算法的迭代,无关变量被删除,ε随之增大,当ε∈[]0.4,1时,建模方法自动切换为Bidiag2 算法;当ε>1 时,切换为VSIRK-PLS 算法;另外当变量数少于60 时应选择Bidiag2算法。Bidiag2算法已被证明所建模型更加精确,且速度较快[23]。为建立准确的校准模型,大部分冗余变量被剔除,从而提高迭代初期建模效率和精度。而在迭代后期切换到Bidiag2 算法可以有效地克服部分变量缺失带来的模型不稳定问题。这种切换策略不光考虑了时间成本,也符合模型间竞争的特性。

图1 SIRK-PLS融合MPA变量选择的算法
2 数据集与软件
本文采用公开的m5 近红外光谱仪测量的60 个玉米光谱标称数据集对所有模型进行验证(https://www.eigenvector.com/data/Corn/index.html)。图2 显示了玉米近红外光谱,光谱波长范围为1100~2498 nm,每2 nm 一个数据点,由700 个波长变量组成。本研究以玉米中蛋白质含量为标称值。所有测试程序通过Matlab R2020a完成。仿真计算机CPU型号为Intel i9-12900K,内存为64 GB,操作系统为Windows 11。

图2 玉米近红外光谱图
3 分析与讨论
BOSS 算法是由MPA 和加权自举抽样的思想衍生而来。首先通过对变量进行加权采样,得到不同变量空间的子集,并对每个子集建立一个PLS 子模型。其次统计交叉验证均方根误差(Root Mean Squared Error of Cross-Validation,RMSECV)前10%子模型中每个变量的回归系数,作为下一轮变量加权采样的权值。如此重复迭代,实现变量空间的软收缩并逐步提取特征变量。
为了验证SIRK-PLS 建模方法的性能,将其与BOSS算法融合,如图3所示为SIRK-PLS在BOSS算法中的应用方案。作为对比,将DSPLS、SIMPLS、PLSHY、Bidiag1和Bidiag2等算法分别用于BOSS算法的PLS建模。表1 简要介绍了这几种PLS 算法。模型的评价指标为RMSECV和各算法运行时间(单位为s):

表1 不同PLS算法的比较

图3 SIRK-PLS在BOSS算法中的应用方案
式中:yi和ŷi分别是实际值和预测值。
3.1 不同建模算法的速度和精度比较
通过复制扩展原始玉米数据集的样本数和变量数,获得不同尺寸的数据集,以此对不同建模算法在不同尺寸数据集上的性能进行测试。对样本扩展后,测试结果如表2 所示。随着样本数量的增加,所有算法的RMSECV 最终都在减小,这说明即使是通过在行方向的复制来增加训练样本数也可以有效提高建模效果。对于任意尺寸的数据集,NIPALS 基本上均为时间开销最大的算法,而表1 中后5 种算法运行时间大约为NIPALS算法的1/2,选择效率得到了大幅提高。但是DSPLS 与SIMPLS 算法的RMSECV 在30000×700 的数据集上较大,预测精度低。另外在60×700 的数据集上,Bidiag2 算法建模速度最快,Bidiag1 算法的RMSECV 最小。在尺寸为600×700 的数据集上,VSIRK-PLS 算法运算时间仅为NIPALS 算法的1/3,在尺寸为30000×700 的数据集上,其运算时间仅为NIPALS 算法的1/4。VSIRK-PLS 算法通过索引技术提高了建模效率,且随着样本数量的增大,优势越大。SSIRK-PLS 算法由于不适合计算大样本数据集而变得十分缓慢,因此不做记录。

表2 在大样本数据集上不同PLS算法的性能对比
保持样本数不变,对变量扩展后,测试结果如表3所示。随着变量数的增加,所有算法的RMSECV最终都在增加,因为通过列方向复制扩展,这相当于给每个样本中增加了大量的共线性变量,导致了较差的建模效果。与表2结果相同,几种改进的PLS算法运行时间相较NIPALS 算法大幅缩减(VSIRK-PLS 算法由于不适合计算多变量数据集而变得十分缓慢,因而例外)。但DSPLS、SIMPLS、PLSHY、Bidiag1 和Bidiag2 算法是通过减少缩放来提高建模效率,未能从本质上避免子模型的重复建立。当面对海量数据时,对建模速度的提升是有限的。SSIRK-PLS算法在多变量数据集上速度最快,且运算速度优势随变量数的增加而更加明显。
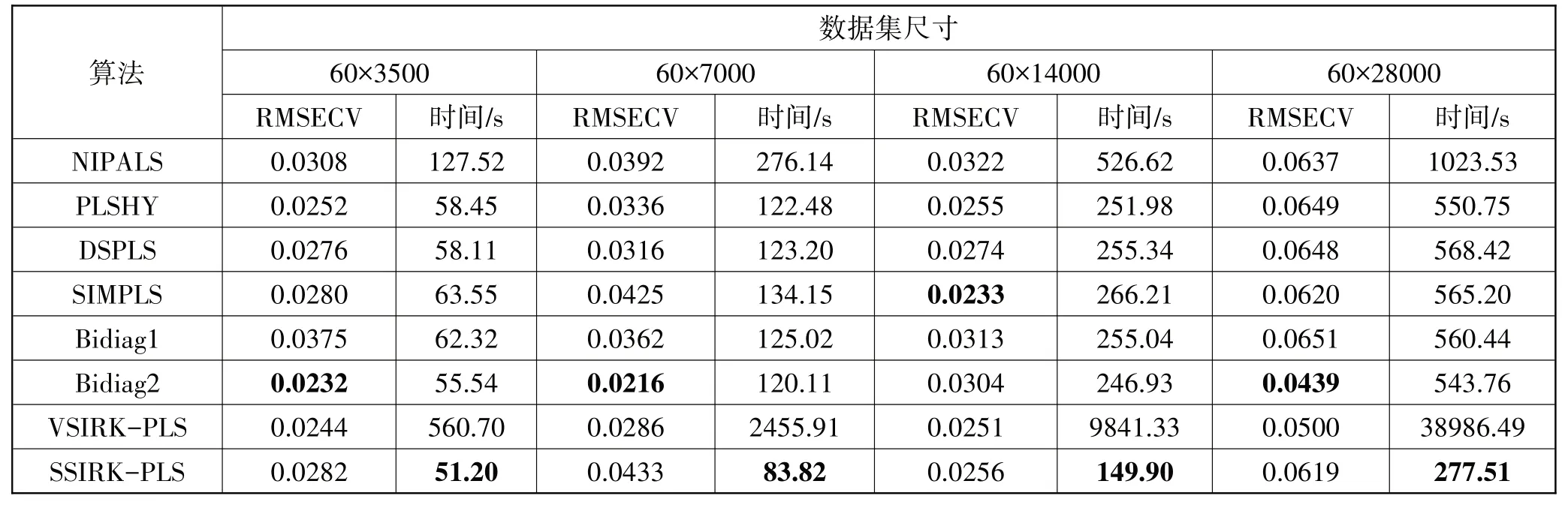
表3 在多变量数据集上不同PLS算法的性能对比
3.2 SIRK-PLS中不同建模算法最优切换条件验证
为了验证SIRK-PLS 建模方法中VSIRK-PLS、Bidiag2及SSIRK-PLS算法的切换阈值,图4对比了变量选择过程中每轮迭代时间与ε的关系。在尺寸为6000×700(ε=8.5)的数据集上,不同算法的测试结果如图4(a)所示。VSIRK-PLS 算法在变量选择迭代初期的速度明显快于NIPALS 和Bidiag2算法,因此首先选择VSIRK-PLS 算法建模。但随着BOSS 算法的迭代,无关变量被剔除,ε逐渐增大,其优势不断缩小。当ε>100 时,即变量数少于60 时,Bidiag2 算法比通过索引协方差矩阵来估计回归系数效率更高,同时考虑模型的稳定性,此时应切换到Bidiag2 算法。在尺寸为60×14000(ε=0.0043)的数据集上,不同算法的测试结果如图4(b)所示。在变量选择初期SSIRK-PLS 算法速度最快;当ε>0.4 时,模型标定方法也应由SSIRK-PLS算法切换到Bidiag2算法。
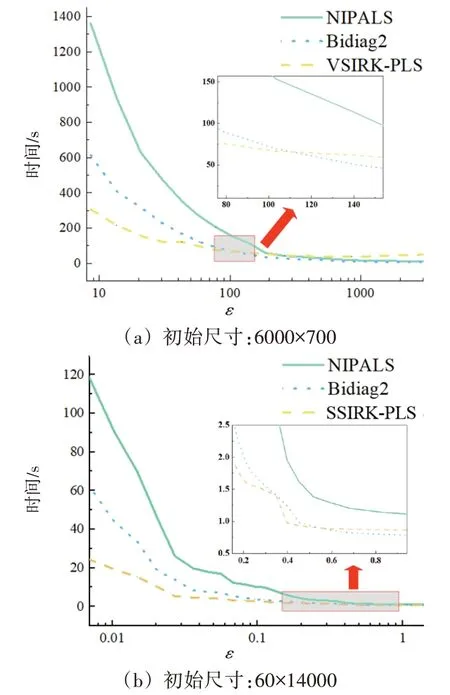
图4 每轮迭代时间与ε的关系
图5 (a)为各种PLS 算法在变量选择过程中每轮迭代时间的对比。可以看出,SIRK-PLS 建模方法在初始大小为1200×28000(ε=0.043)的数据集上首先选择了速度最快的SSIRK-PLS 算法。随着变量选择进行,ε逐渐变大,SIRK-PLS 建模方法都选择了最优的PLS 算法,整体运算时间最短,实现了全局最优的建模算法自适应切换。图5(b)为各种PLS 算法与NIPALS 算法的RMSECV 之比,由于SIRK-PLS 建模方法是基于协方差估计的,没有通过矩阵缩放计算加载和得分向量,因此会损失部分精度。SIRK-PLS 建模方法的RMSECV 并不是最优的,但与NIPALS 算法的RMSECV 之比接近为1。所以SIRK-PLS 建模方法的切换策略并不影响BOSS算法对变量空间的竞争筛选,考虑到计算效率的大幅提升,SIRK-PLS建模方法的预测结果是可信赖的。

图5 各种PLS算法的每轮迭代时间及其与NIPALS算法的RMSECV之比(初始尺寸:1200×28000)
4 结束语
本文提出的SIRK-PLS 建模方法通过索引技术对协方差矩阵进行重用,使同一数据集中多个变量子集的PLS回归拟合成本显著降低,提高了建模和预测的计算速度。将SIRK-PLS 与BOSS 算法融合进行标定建模,在玉米近红外光谱数据集进行验证,结果表明SIRK-PLS 为速度最快的模型标定方法,对于尺寸越大的数据集,此建模方法优势越大。虽然本文研究仅在BOSS算法上进行验证,但这是一种通用策略,也可以推广到其它需要评估大量子集的变量选择算法中,为各种优秀的变量选择策略应用到过程监控等方面提供支持。
