聚类质心与指数递减方法改进的哈里斯鹰算法

白晓波，江梦茜，王铁山，邵景峰，李 勃

（1.西安工程大学管理学院，陕西 西安 710048；2“.一带一路”纺织发展创新研究院，陕西 西安 710048；3.福州大学先进制造学院，福建 福州 350003）

0 引 言

群体智能优化算法（Swarm Intelligence Optimization Algorithm，SIOA）是模拟生物种群的群体或社会行为，求解问题的最优值，在工程、医学、军事和生产车间调度等领域均有应用。为了解决不同类型的优化问题，如在参数取值范围内，参数多、维度高，优化目标为单峰或者多峰函数，产生了一些比较有代表性的群体智能优化算法，如粒子群算法（Particle Swarm Optimization，PSO）［1］、灰狼算法（Grew Wolf Optimization，GWO）［2］、烟花算法（Fireworks Algorithm，FWA）［3］、蛙跳算法（Shuffled Frog Leaping Algorithm，SFLA）［4］、萤火虫算法（Firefly Optimization Algorithm，FOA）［5］和果蝇优化算法（Fruit Fly Optimization Algorithm，FFOA）［6］等。这些不同的优化算法在不同的优化目标上的性能表现差异较大。这也比较符合无免费午餐（No Free Lunch，NFL）定理［7］，即一个算法很难在每个优化目标上表现出优异性能。这也是很多学者一直在改进现有算法或者研究出更有效的优化算法的原因。

2019 年，Heidari 等［8］提出了哈里斯鹰优化（Harris Hawks Optimization，HHO）算法，该算法通过模拟猎物的逃逸能量来控制全局和局部搜索，但是算法存在前期全局搜寻能力较弱、且种群多样性不足的问题。与GWO 相比，对部分多峰函数优化性能较差。因此，国内外学者对HHO 进行了研究，并改进其寻优能力。如贾鹤鸣等［9］，将动态反向学习的阿奎拉鹰（Aquila Optimizer，AO）［10］与HHO 相融合，解决了HHO 全局寻优能力不足的问题，在对部分多峰函数的求解中，取得了和AO 近乎接近的结果。汤安迪等［11］利用精英等级策略和非线性能量因子对算法进行改进。高建瓴等［12］主要利用混合差分与二次插值的方法对HHO 改进。朱诚等［13］提出趋化校正的HHO。刘小龙等［14］利用方形邻域和随机数组对HHO改进。Wang 等［15］提出了一种离散HHO 解决充电的共享电动汽车调度问题。Song 等［16］以Tent 混沌映射和随机游走机制改进HHO。国外学者的研究，如Elgamal 等［17］利用混沌映射初始化种群，增加种群多样性，再用模拟退火（SA）算法对当前最佳解进行优化，以提高HHO 的利用率。Nandi 等［18］将HHO 和GWO相结合，利用GWO 算法进一步改进了HHO 算法的探索和开发阶段。Hussien 等［19］将反向学习、混沌局部搜索和自适应技术相结合，提高了HHO 的性能。Kamboj 等［20］基于正余弦算法改进HHO 的探索阶段，提出了混合Harris Hawks 正余弦算法。Kaveh 等［21］将帝国主义竞争算法（Imperialist Competition Algorithm，ICA）［22］与HHO 相结合，构成混合优化算法ICHO。Gupta 等［23］利用非线性能量参数、差分进化、贪婪选择机制和反向学习等提高了算法的搜索效率。

综上，国内外学者都针对HHO 搜寻能力不足的问题进行研究，并取得了较好的效果，主要方法为：1）将HHO 中线性能量参数改进为非线性，并加入精英选择策略。2）将全局寻优能力好的算法和HHO 结合，构成混合优化算法。3）引入混沌方法，改进种群多样性。但是在改进中都忽略了HHO 在更新种群位置的时候，用了种群均值，这就存在部分偏离最优值位置较远的种群对均值产生较大影响，进而影响到迭代时下一代的种群分布，导致算法难以较快收敛于最优值。因此，本文提出新的假设，即将所有种群看作一类，利用聚类簇心代替均值，能够使算法较快地收敛于最优值；再结合非线性能量参数改进全局搜寻能力，能够取得更好的优化效果。

1 哈里斯鹰优化算法

哈里斯鹰优化算法是模拟哈里斯鹰围捕猎物的过程，利用猎物的逃逸能量来控制探索与开发阶段的转换。HHO详细的数学表示如下。

1.1 探索阶段

探索阶段（|E| ≥1，E为猎物逃逸能量），使用等概率的2种方式更新种群位置，如公式（1）所示。

1.2 探索开发转换

HHO是线性的逃逸能量计算方式，如公式（2）所示：

其中，T为最大迭代次数，E0为（-1，1）之间均匀分布的随机数。

1.3 开发阶段

开发阶段（|E| < 1）是在发现猎物后采用的抓捕策略，HHO 利用猎物逃逸能量E和（0，1）之间均匀分布的随机数来控制4 种抓捕策略，如下所示。其中，r是（0，1）之间均匀分布的随机数。

1）软包围。

若|E| ≥0.5 且r≥0.5，则使用软包围策略。猎物有逃逸能力，但无法逃脱。公式如下：

其中，ΔX(t)表示当前最优值与种群X的差，其中r5∈（0，1）为随机数，J为猎物逃脱时的随机逃逸距离。

2）硬包围。

若|E| < 0.5且r≥0.5，则使用硬包围对策。即猎物没有足够能量逃逸，且无逃出机会。公式如下：

3）渐进式快速俯冲软包围。

若|E| ≥0.5 且r<0.5，表示猎物有足够能量，且有机会逃逸。此时，需使用2 种策略，如公式（7）~公式（9）所示：

式中，d表示问题维度，S表示d维的随机向量，Levy（·）表示Levy 飞行函数，详见文献［11］。Levy（d）表示由Levy 飞行函数返回的d维向量。由此，种群更新公式如下：

其中，f（·）为优化问题的适应度函数。

4）渐进式快速俯冲硬包围。

若|E| < 0.5 且r<0.5，表示猎物逃逸能量不足，但有逃脱机会，因此，使用硬包围，快速缩小种群和猎物之间的距离。公式如下：

2 种群质心和非线性能量改进HHO

2.1 改进HHO的基本思想

1）聚类质心改进HHO。基本思想是：将HHO 的种群X视作需要分类运算的一个矩阵，只是划分时K=1，即本质上并未分类，但是，取得了种群的质心，利用种群的质心代替HHO 中的种群均值X（t），以减少部分远离最优值的种群在进行均值运算后，对均值产生放大效应，使得算法不能快速收敛。

种群质心的获取，使用Matlab2017 中的Kmeans［24］算法。在输入参数值的选择上，必定会影响到最后的簇心，对HHO 的影响主要体现在算法寻优性能上。具体的影响和选取方式在后续实现仿真中会详细阐述。

2）非线性能量改进HHO。在HHO 中，通过能量逃逸公式（2）控制探索与开发阶段，也就是该公式决定了HHO 的全局和局部寻优次数。根据公式（2）绘制的能量变化过程如图1所示。

图1 线性递减能量变化曲线图

图1 是一个种群数为20、迭代次数也为20，生成400个点构成的能量变化曲线。|E|≥1，HHO进行全局寻优。从图1 可以明显看出，其整个寻优过程中，|E|≥1的次数很少，必然影响到HHO全局寻优能力。这就导致在面对多峰函数时，寻优效果较差，易陷入局部极值。为了增加其全局搜寻能力，需要改进能量计算方法，使用指数递减的计算方法［25］，公式如下：

其中，Emin为能量最小值，Emax为能量最大值，c为一常数，在本文中c=0.1。其能量变化曲线如图2所示。

图2 指数递减能量变化曲线

在图2 中，可以明显看出 |E|≥1 的次数明显增加，即使到了中间阶段，也存在 |E|≥1 的情况。迭代后期，进入局部寻优阶段，所采用的种群更新策略也较线性递减更为全面。在图1 中，进入迭代后期主要是 |E|≤0.5 的情况，而在图2 中，|E|≤0.5 和 |E|> 0.5的情况比较均衡，这就更有利于搜寻到最优值。

2.2 KmHHO算法

基于2.1 节中的改进思想和方法，得出改进的HHO算法（记作：KmHHO）流程如图3所示。

图3 KmHHO算法流程图

KmHHO算法的详细过程如下。

步骤1种群初始化。根据参数取值范围［lb，ub］和维度d，随机生成N个d维种群，并设置主要参数Emax=2、Emin=0.0001及最大迭代次数T。

步骤2进入迭代。

步骤3若t=T，程序结束，否则返回步骤2。

2.3 KmHHO算法时间复杂度

在KmHHO 中增加了Kmeans 算法计算簇类质心，其时间复杂度为O（RNDK）（R：迭代次数，N：数据个数，D：数据特征维度，K：类簇数），会较大程度地影响KmHHO 的效率，非线性递减能量计算公式并不影响。在本文中，加入了Kmeans，但是K=1，R待定，N和D由具体问题决定。则KmHHO 的算法时间复杂度表示为O（2TN+TNRD）。根据NFL 定理，算法性能提高，增加了一定时间开销，这也是可以接受的。

3 实验仿真

实验仿真选择了23个benckmark 基准函数，详见文献［2］。整体分为3 个部分：1）分析Kmeans 算法优化后的HHO 性能，并分析Kmeans 不同取参对寻优结果的影响。2）将KmHHO与GWO［2］、HHO［8］、DAHHO［9］和AO［10］在相同种群数N、最大迭代次数T和运行次数runs下的均值、标准差进行对比分析，均值越小，寻优性能越好，标准差越小，算法越稳定。3）Wilcoxon秩和检验［26］，以检验KmHHO算法与其他算法的差异性。

所有实验运行环境为：Windows 10 操作系统（64位）， Matlab2017a， Anoconda3。 Intel（R） Core（TM）i5-7400 CPU@3.00 GHz，4 GB 内存。为了与主要参考文献的实验数据公平对比，将迭代次数T、种群数N和每个算法独立运行次数runs 设置为与文献［9］相同，即T=500、N=30、runs=30。

3.1 聚类质心优化HHO后的寻优结果

用Kmeans 聚类质心代替HHO 均值后，是否能够提升算法寻优性能，若能提升，又能提升多少。这里需要进一步说明。对此，本文将加入Kmeans 的HHO与原HHO 在23 个基准函数上进行效果对比。为了统计方便，在23 个基准函数中，只要获得最优值，即使和其他算法相同，也算作胜出。实验结果如表1 所示。其中，粗体表示最优值。

表1 使用Matlab的Kmeans聚类质心改进HHO与原HHO的对比

在表1 中，除了′Distance′=′sqEuclidean′时的avg的胜出数分别为9 和10，其他2 种情况的胜出数均高于原HHO，说明通过Kmeans聚类质心改进HHO的可行性。后续实验选择胜出最多，且稳定性较高的参数配置′Distance′=′cityblock′、′start′=′Uniform′。

3.2 KmHHO与其他算法性能对比

这里主要分析在HHO 加上Kmeans 和指数递减的能量计算方式后对算法性能的影响。主要与GWO［2］、HHO［8］、DAHHO［9］、AO［10］这4 种算法作对比。实验结果如表2所示。其中，粗体表示最优值。

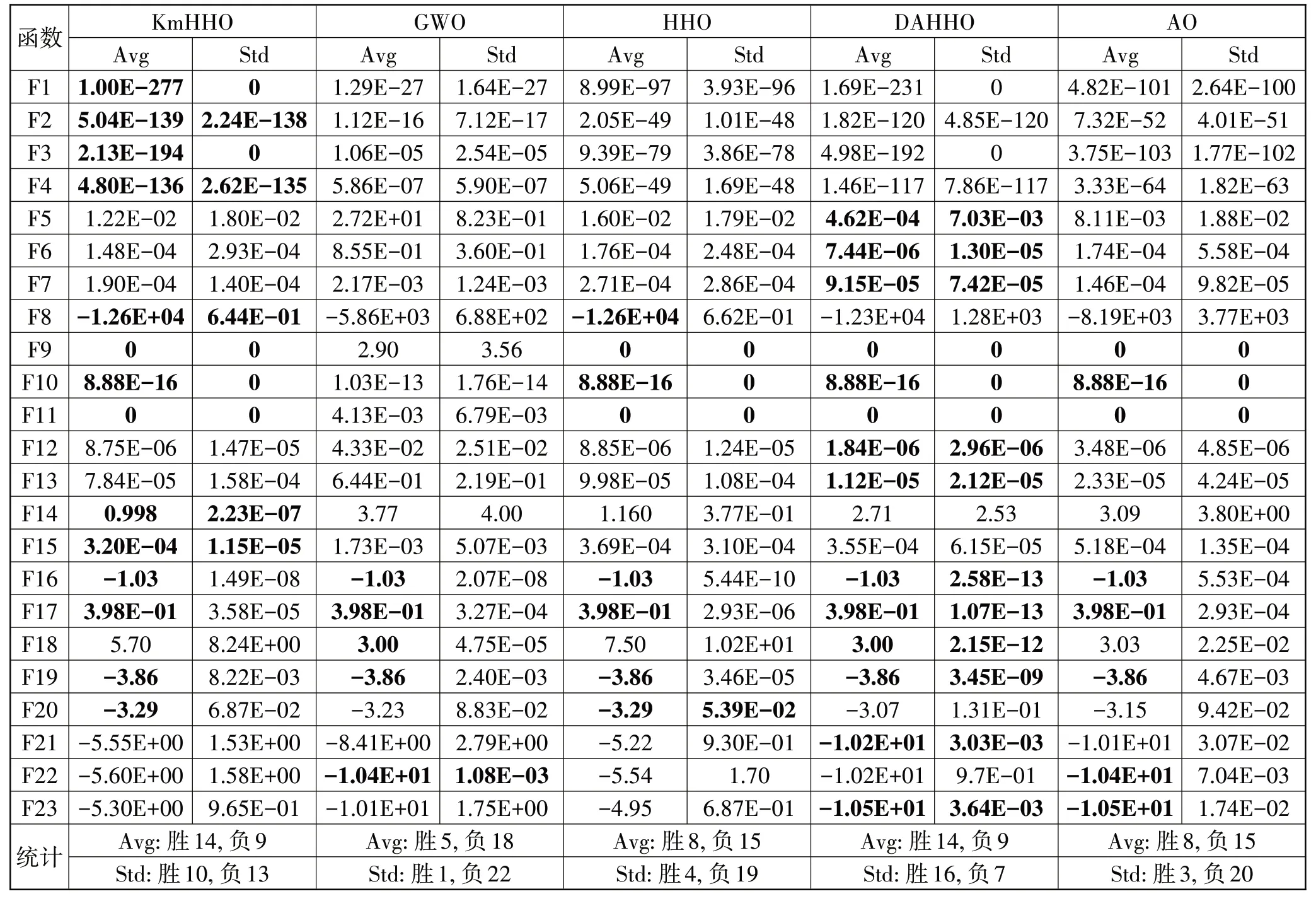
表2 KmHHO与其他4个优化算法性能的对比

表2中的KmHHO 这一项，是在Kmeans聚类质心优化HHO 后，再加上指数递减逃逸能量的改进效果，与表1 中的数据相比，寻优精度有了进一步提升。如在函数F1~F4、F20~F22等，这也说明了使用指数递减的逃逸能量比原HHO中线性递减的逃逸能量更好。

从表2 的统计数据可以看出KmHHO 在23 个benckmark 函数中，共在14 个函数上取得了最优值，比HHO 提高了6 个函数，整体效果明显优于GWO、HHO 和AO，从而说明Kmeans、指数递减的逃逸能量对HHO 的改进有着良好的效果，比DAHHO 的胜出少1 个。但是，KmHHO 在单峰和多峰的高维函数上有很好的寻优效果，如F1~F4、F8~F11、F14~F17、F19和F20，而在F21~F23 的寻优效果上明显低于GWO、DAHHO 和AO。这也符合NFL 理论，一个寻优算法，很难在所有优化目标上都有良好性能。

3.3 Wilcoxon秩和检验

Wilcoxon 秩和检验［26］，用来检查2 个算法之间的差异性。设显著性水平为5%，若p<5%，则零假设被拒绝，表明2 个算法之间存在显著性差异；否则，表明2 个算法性能相当。KmHHO 与其他4 个算法的Wilcoxon 秩和检验的结果如表3 所示。针对每个算法、每个函数的30 次寻优结果，使用Python 的scipy.stats.ranksums（）方法计算可得。

表3 KmHHO与4个算法Wilcoxon秩和检验结果

在表3 中，粗体是p>5%的，表明KmHHO 与相应算法在对应函数上性能相当，其他表示有显著差异。如HHO列，在函数F5~F13上与KmHHO性能相当，其他函数上具有显著差异。这也比较符合表2的测试数据。

由上述算法精度测试和统计检验，说明通过Kmeans和非线性递减能量改进的KmHHO，在全局探索和局部开发能力上比GWO、HHO 和AO 都有了较大幅度的改善，存在的不足之处是略微弱于DAHHO。

4 结束语

本文通过Kmeans 簇类中心代替HHO 中的均值、指数递减能量代替线性递减能量这2种方法，将HHO算法的性能进一步提升，使其全局和局部寻优能力都得到增强，并与4 个算法的性能进行了对比，综合与GWO、HHO 和AO 比较，在寻优精度和稳定性上，都取得了绝对优势，并通过Wilcoxon 秩和检验，得出KmHHO与GWO、HHO、DAHHO和AO在23个函数上的差异性。差异性检验的结果，也与性能对比相吻合。但是，算法在部分多峰函数上的寻优结果虽有提高，依然不是非常理想，这也是后续继续开展研究的方向，以更进一步提升KmHHO 的综合性能。另外，需要紧密结合工程设计问题，进一步对算法的性能进行验证，以体现其工程适用性。