直接法切入应用,间接法巧妙转化—一道双曲线题求解的探究
2024-01-19许姗姗
许姗姗
江苏省宜兴市张渚高级中学 (214233)
圆锥曲线中的取值范围(或最值)问题,一直是各类数学考试中比较常见的基本题型.此类问题中,往往涉及圆锥曲线中的基本要素(离心率,直线的倾斜角或斜率等)、相关点的坐标、对应的参数值、相应的代数式等问题,形式多变,创新新颖.同时,问题场景可“动”或“静”,可“数”或“形”,充分体现了解析几何中“动”与“静”的完美统一,“数”与“形”的有机融合,综合性强,趣味性高,能更好地体现数学的基础性、综合性与应用性等,倍受各方关注.
1.问题呈现
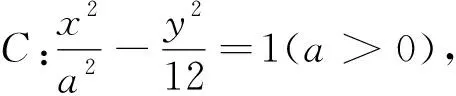
此题以含参双曲线为问题背景,结合焦点弦长度的给出,利用直线与双曲线的位置关系的合理创设,通过符合条件的焦点弦所在的直线的条数,进而巧妙创新确定对应参数的取值范围.求解时可从问题条件入手,合理挖掘问题的本质与内涵,既可直接“翻译”条件,直接法切入应用;也可间接“处理”条件,间接法巧妙转化.不同的思维视角,都可以给问题的解决提供有效的技巧与方法.
2.问题破解
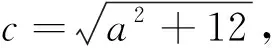
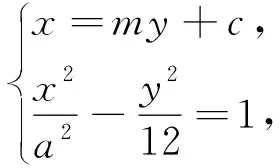
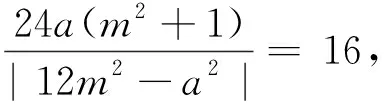

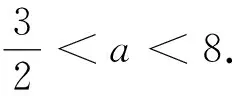
方法2:(直接法2)由方法1可得关于m的方程3a(m2+1)=2|12m2-a2|有四个不等的实数解,当12m2-a2>0时,可得3a(m2+1)=2(12m2-a2),即(24-3a)m2=2a2+3a,因为a>0,可得24-3a>0,解得0 解后反思:根据题设条件加以直接“翻译”,通过直线与圆锥曲线的位置关系,利用基本量的分析与处理来解决问题,此种思维方法对数学运算提出了较高的要求,往往数学运算量比较大,过程比较繁杂.直接法也是解决直线与圆锥曲线的位置关系问题中的一种基本解法,也是最为常用与首选的方法. (2)弦的两端点分别在双曲线C的左、右支上,此时直线有两条.当直线l与x轴重合时,|AB|取得最小值2a,要使得直线l有两条,则必须满足2a<16,即a<8. 解后反思:根据题设条件加以间接“处理”,利用圆锥曲线的对称性以及相应的几何性质,这里特别要熟悉双曲线弦的最值问题,通过两极端情况加以极限思维处理,从而得以确定参数的取值范围.间接法的本质就是抓住圆锥曲线自身的对称性以及几何性质,为巧妙解决涉及直线与圆锥曲线的位置关系问题提供一种更加良好的解法,优化解题过程,减少数学运算. 由以上双曲线问题的“一题多解”,可进一步发散思维,开拓技法,从符合条件的焦点弦所在直线的条数变化入手,进行“一题多变”. 一般地,涉及直线与圆锥曲线的位置关系问题中,有关圆锥曲线中的取值范围(或最值)问题的几种常见求解策略有: (1)利用圆锥曲线自身的几何性质、函数与方程思想中的判别式等构造不等关系,从而确定参数的取值范围; (2)利用题设已知参数的取值范围,进而确定新参数的取值范围,解决这类问题的核心是建立已知参数与新参数这两个参数之间的等量关系,合理巧妙转化; (3)利用题设中的隐含不等关系建立对应的不等式(组),从而求解相应参数的取值范围; (4)利用题设中的已知不等关系建立对应的不等式(组),从而求解相应参数的取值范围; (5)利用求解函数值域的方法将待求变量表示为其他变量的函数,求其对应的值域,从而确定参数的取值范围. 在平时数学教学中,“一题多解”对学生数学基础知识的构建与逻辑思维能力的培养等方面都有着重要的影响.教师应注重将“一题多解”应用意识合理、适度地渗透到数学课堂解题教学中. 借助“一题多解”的应用,可以从不同思维角度进行数学问题的解法探究,让学生在解题探究中感悟数学思想方法之美,同时结合“一题多变”,达到“一题多得”,“一题多思”等良好效果,开拓解题的宽度、广度、深度等,培养学生思维的发散性与开拓性,全面开拓学生的视野,提升数学能力与数学品质,培养学生的核心素养.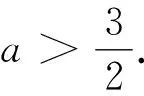
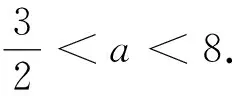
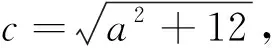

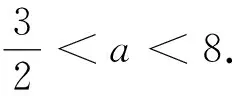
3.变式拓展
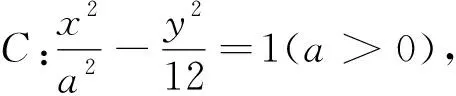
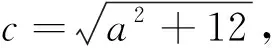
4.教学启示
4.1 合理归纳总结,技巧方法点睛
4.2 倡导“一题多解”,培养核心素养
