基于FPGA的电力电子恒导纳开关模型修正算法及实时仿真架构

王钦盛，王 灿，潘学伟，梁 亮

（哈尔滨工业大学（深圳）机电工程与自动化学院，广东省深圳市 518055）

0 引言

近年来，中国传统电力系统正在向以新能源为主体的新型电力系统转型。随着新能源发电接入比例的不断提高，电力系统中的电力电子设备也在不断增加［1］。在电力电子设备的研究中，电磁暂态实时仿真是电力电子系统设计和测试的安全可靠工具［2-3］，可以减少硬件实验的开销并缩短研发周期［4］。

实时仿真的严格时序要求使得其难以兼容离线仿真中的插值算法，原因是插值算法会使仿真算法的复杂度急剧增加，增大仿真的步长［5］。在没有插值算法的修正时，为了保证电力电子系统中开关元件换向的准确性，仿真的时间步长要比离线仿真小得多，一般要求在微秒级甚至亚微秒级［6］。现场可编程门阵列（field programmable gate array，FPGA）因具有天然的高度并行性、出色的计算能力和极低延迟的特点，已经成为实时仿真以及硬件在环测试的常用计算加速硬件［7-10］。

目前，为实现基于FPGA 的电力电子实时仿真，需要解决以下3 个技术要点：

1）电磁暂态仿真算法。为了满足电力电子系统仿真测试的需求，实时仿真中所使用的算法一般不能太复杂。因此，以节点分析法为基础的电磁暂态程序（electro-magnetic transient program，EMTP）算法成为了应用和研究的主流算法。为了充分发挥FPGA 的计算加速优势，需要对传统的离线EMTP进行改进［11］。文献［6］针对固态变压器的实时仿真应用提出了一种紧凑型节点分析法，实现了50 kHz固态变压器的实时仿真。然而，为了适配定点数运算，电路元件采用混合建模方式，增加了建模复杂度。

2）开关模型的虚拟功率损耗。在上述算法中，电力电子开关通常采用伴随离散电路（associated discrete circuit，ADC）模型中的恒定导纳模型［12］。该模型不仅可以很好地模拟出理想开关的稳态特性，同时使得实时仿真过程中无须更新电路的计算导纳矩阵，极大地降低了实时仿真过程中的计算负担。但恒导纳开关模型也存在理想开关不存在的暂态振荡，在仿真过程中引入了由模型所导致的功率损耗，而不是电力电子设备产生的实际功率损耗，称为虚拟功率损耗。为了减小虚拟功率损耗对仿真准确性的影响，相关学者根据不同的数值方法和拓扑提出了改进的恒导纳开关模型，但开关动作时的暂态振荡仍然存在，不能完全消除虚拟功率损耗［13-14］。此外，也有研究人员通过在该模型中加入补偿电压源和电流源的方式来补偿由原模型引入的虚拟功率损耗［15］，或引入重新初始化算法来抑制开关暂态振荡［16］。然而，补偿源的求解依赖外电路参数，初始化算法的设计不够简单高效，都增大了FPGA 逻辑和存储资源的负担。

3）FPGA 的实现方法。不同于运行在个人计算机上的离线仿真，基于FPGA 的实时仿真需要将模型和算法硬件编程后下载到FPGA 硬件中进行布局布线实现。文献［17］提出了一套基于FPGA 的有源配电网实时仿真方法论，详细介绍了算法在FPGA 中的实现过程。但其使用的传统开发工具门槛较高，同时缺少对资源利用规划的研究。受益于高级语言综合（high-level synthesis，HLS）工具的发展，FPGA 实现上的门槛降低，同时开发者对其的利用能力提高［18］。因此，通过HLS 工具设计合理高效的FPGA 算法架构是可行且有必要的。

以上3 个方面是基于FPGA 的电力电子实时仿真中的技术要点以及挑战。本文首先基于传统的离线仿真算法改进，推导了一种简洁EMTP 算法。其次，根据所设计的算法流程，从数值算法的角度讨论了开关模型虚拟功率损耗的来源，以此为基础提出了一种初始误差修正算法，可以基本消除由开关模型引入的功率损耗，算法流程简单高效，无须依赖外电路参数，具有普适性且几乎不消耗额外的FPGA资源。最后，设计了一种FPGA 的实现架构，在基于FPGA 实现所提算法的基础上提高了FPGA 的资源利用效率，同时并不影响仿真速度。

1 基于EMTP 的实时仿真算法

1.1 电路元件建模

在以EMTP 为基础的实时仿真算法中，电路中的动态元件以及开关器件通常需要根据不同的数值方法离散化，建立为ADC 模型的形式［12］。如图1 所示，电路各动态元件被建模为等效支路导纳Yb和伴随电流源ja。

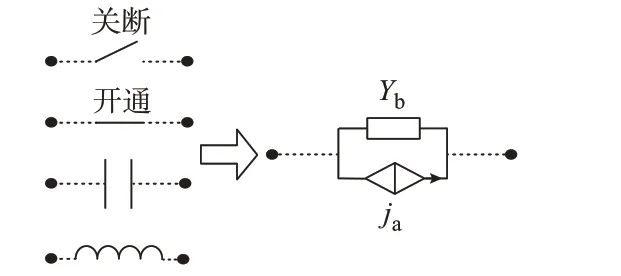
图1 电路元件的ADC 模型Fig.1 ADC model of circuit components

文献［16］将ADC 模型中的伴随电流源参数化，不同的元件表达式可以整理为统一的参数化形式：

式中：vb为支路电压；ib为支路电流；Δt为仿真步长；α和β为元件系数。

式（1）中各参数的取值与元件类型和数值离散方法相关。其中，后向欧拉法具有极强的数值稳定性和高收敛性，已被广泛应用于电磁仿真算法中，现有开关模型的研究大多都来自二值LC 等效模型的改进。采用以上方法的不同元件表达式系数如表1所示。表中：L为电感元件自感量；C为电容元件电容量；Lswitch为模拟开关导通的电感元件自感量；Cswitch为模拟开关关断的电容元件电容量。

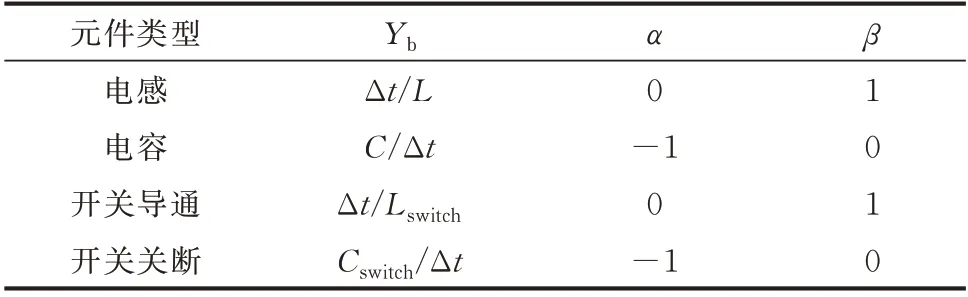
表1 不同元件表达式系数Table 1 Expression coeffients of different elements

文献［13-14］所提出的改进型恒导纳开关模型都可以通过改变表1 中开关元件的系数来实现。

上述元件转换为ADC 模型后，还需要将电路中的电压源转换为诺顿等效形式，即可通过EMTP 算法进行电路的时域仿真求解。

1.2 简洁EMTP 算法

传统的EMTP 是基于节点分析法设计的，根据节点分析法，节点电压计算方法如下：

式中：vn为节点电压向量；Yn为电路的节点导纳矩阵，当开关使用恒定导纳模型时保持不变；in为节点注入电流源向量。

根据电路理论中的网络图论［19］，可以引入节点-支路关联矩阵A来帮助in的矩阵化计算，有

式中：n为电路节点数；b为支路数。当支路电流流出节点时，ail=1（i=1，2，…，n；l=1，2，…，b）；当支路电流流入节点时，ail=-1；当节点与支路无关联时，ail=0。

此时有：

式中：ja为支路伴随电流源向量；js为独立电流源或电压源支路的诺顿等效注入电流源向量。

传统EMTP 的计算程序可整理为下列算式：

式中：itemp为临时电流向量，用于储存各支路的电流源之和以便后续计算；Yb为支路导纳矩阵；vb为支路电压向量；ib为支路电流向量；α和β为元件系数对角矩阵。

式（5）—式（9）中的各个算式相互串联，具有高度串行性，不适用于基于FPGA 的并行化实时仿真计算。因此，需要推导一种可并行化的计算流程。

在电磁仿真中，更需要电路的电气量输出，如vn、vb和ib。因此，中间计算过程可以合并，得到：

合并后，式（10）—式（12）中各系数矩阵均为常系数矩阵，可预先计算，故其中各电气量相互解耦，可独立计算。

将式（11）、式（12）代入式（9）中化简整理可得：

支路电流向量ib包含了仿真电路中全部支路的电流信息，通常情况下已经能够满足用户的观测需求，且与式（13）串联，需要在仿真计算过程中保留。

实际应用中，用户通常需要通过添加电压表或电压测点等测量元件来获取所需电压量。因此，仅输出vn和vb无法直接满足用户需求，且其中包含了无须观测和仿真计算过程中非必要的量，浪费了计算资源。在仿真建模时，通常选择接地节点为参考电压节点，此时用户观测电压可直接为节点电压或两节点电压之差：

式中：vm表示观测电压；vn表示节点电压；i和j为节点编号；m为电压测量点数量。

整理可得：

式中：vm为观测电压向量；M为m×n观测矩阵。根据式（11），当M=AT时，vm=vb。通过式（15）可直接输出电压测量点结果，满足用户需求。

合并式（12）和式（15）中的常系数矩阵为中间矩阵：

式中：B为m×b矩阵；C为b×b矩阵；E为b×b单位矩阵。

根据式（5）和式（12）—式（16），可整理得新仿真计算步骤：

式（17）中各算式的串行度降低，vm和ib可以并行计算，舍去了非必要的计算量和步骤，提高了算法流程的简洁性，更加适用于基于FPGA 的实时仿真。

2 恒导纳开关模型损耗消除

目前，相关研究认为恒导纳开关模型的损耗是由储能元件产生的，只要准确计算储能元件的能量变化，就可以测量开关的损耗，并通过优化模型参数的方式降低损耗［20］。

由于本文引入了参数化ADC 模型，现有的优化恒导纳开关模型大都可以通过调整模型中的系数实现，淡化了模型的物理特性。因此，本文从数值算法的角度出发，分析损耗的来源。

2.1 虚拟功率损耗来源分析

随着新能源的发展，电压源型换流器（voltage source converter，VSC）在新型电网中得到了越来越广泛的应用。为了提高普遍性，本文以VSC 为对象展开分析，其桥臂恒导纳开关模型如图2 所示，其系数采用表1 中的二值LC 模型系数。

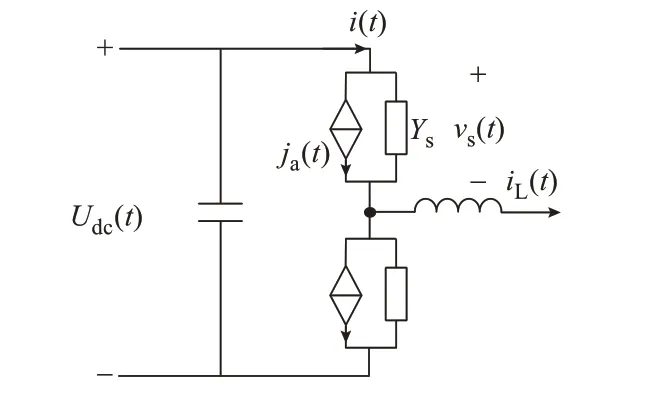
图2 VSC 桥臂恒导纳开关模型Fig.2 Fixed-admittance switch model ofVSC bridge arm

假设上桥臂开关处于关断稳态，在t时刻收到导通信号切换。关断稳态时，桥臂开关电流i（t）为0，电压vs（t）为直流电压Udc（t），因此有：

式中：Ys为开关支路的导纳。

在t时刻，ja根据式（13）中的算式更新，有：

代入导通后的开关系数，ja（t）=0。

导通稳态时，桥臂开关电流i（t）与电感电流iL（t）相等，电压vs（t）为0，因此有：

在理想开关中，开关从关断稳态到导通稳态是瞬时的，没有中间过程，t时刻即达到稳态。而该模型中，t时刻的ja与稳态有一个差值iL（t），称为初始误差。开关从导通切换为关断时则与上述过程相反，初始误差为-YsUdc（t）。

初始误差的存在使得开关状态切换后需要一个收敛至稳态值的过程，收敛过程与初始误差的大小和数值方法有关，这也是虚拟功率损耗产生的原因。根据式（19）可知，ja的更新与初始误差表达式并无直接关联关系，且初始误差值可能因电路工况改变而改变。因此，即使修改开关模型系数也仅能够在某些特定情况下减小初始误差的值，无法从根源上解决这一问题。

2.2 初始误差修正算法

电力电子开关在电路中一般起换流的作用，根据式（18）和式（20），开关稳态电气值与特定支路的电流、电压和开关支路导纳相关。因此，若将开关切换后的ja直接替换为其稳态值则可以消除初始误差，省略收敛过程。

在仿真的算法流程式（17）中，t时刻的ja计算要优先于该时刻的电压、电流，故开关稳态值无法直接获取。如图2 所示，开关稳态值通常与滤波电容电压和滤波电感电流相关，相对于电力电子开关，滤波元件在仿真步长的时间尺度上变换缓慢，可等效为独立源［16］。因此，对于此类元件，可以认为t-Δt时刻与t时刻的值几乎不变，可以近似替代，有文献利用相似思想进行并行化算法的设计并验证［21］。本文基于此设计了一种初始误差修正（initial error correction，IEC）算法，如图3 所示。

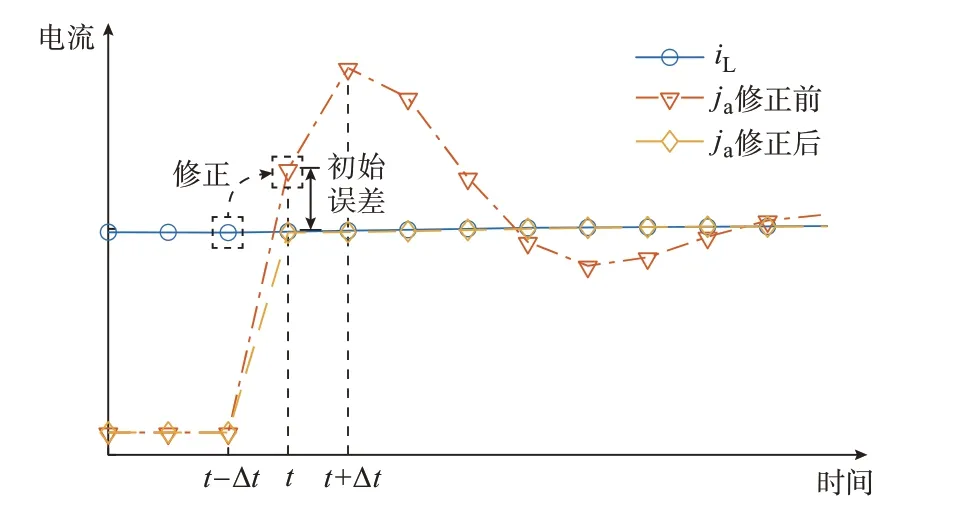
图3 初始误差修正算法示意图Fig.3 Schematic diagram of initial error correction algorithm

对于图2 中的桥臂开关，在t时刻开关状态切换，对应的修正公式如下：

上桥臂：

下桥臂：

为了具有普适性，将式（21）和式（22）整理为：

式中：vb，correct为开关关断后等效并联支路的电压；ib，correct为开关导通后等效串联支路的电流；hon为导通修正系数，其取值与电路建模时ib，correct支路的参考方向相关；hoff为关断修正系数，其取值与vb，correct的参考方向和开关支路导纳相关。其中，等效串联支路一般为电感元件，等效并联支路一般为电容元件。

在导通时，通过t-Δt时刻的电感电流值经式（23）计算后来修正t时刻开关支路的ja，有效地减小了开关切换时刻的初始误差，抑制了暂态振荡过程。同理，在关断时可通过t-Δt时刻的电容电压值来修正t时刻开关支路的ja。

初始误差修正算法中，不同开关的hon和hoff可在仿真建模时确定，整理为向量hon和hoff。vb，correct对应的支路也可在仿真建模时确定，将算法所需电压作为观测电压加入vm的计算中。ib，correct可直接在仿真计算过程的ib中获取。

类似地，在文献［16］中，历史电流源重初始化（history current reinitialization，HCRI）算法通过储存开关上一开关周期中切换后的稳态值（文献中取导通或关断后的第5 个仿真步）来修正本次切换时的初始误差。初始误差修正算法通过上一仿真步中的相关电压和电流来修正初始误差，省略了稳态判断和存储的步骤，在基于FPGA 实现时能够节约硬件资源。同时，与上一开关周期的稳态值相比，上一仿真步的稳态值与本次仿真步的稳态值误差更小，提高了修正精度。

3 FPGA 实现架构

传统的FPGA 开发基于硬件描述语言，入门门槛高，项目周期长，限制了研究工作的开展。Labview FPGA 是一种基于图形化编程语言的HLS工具，基于顶层设计、底层调用的原则实现高效可靠的FPGA 开发，具有编程、仿真、调试一体化功能。本文基于该环境开发了一套基于FPGA 的实时仿真平台。其中，硬件架构如附录A 图A1 所示，该平台包含了FPGA 开发板、PC 主机和DA 转换模块、显示器等外部设备。FPGA 主芯片为Xilinx Kintex-7 XC7K325T，逻辑资源量如附录A 表A1 所示。

FPGA 基于硬件电路实现自定义功能，最终的功能模块都会被映射成芯片中的实际电路。尽管HLS 工具可以帮助研究人员利用高层次语言，从而省去底层开发，然而编译器并不能自动实现资源的高效利用。为了充分发挥FPGA 的优势，提高逻辑资源的利用效率，需要在程序设计时便考虑这一特性。根据简洁EMTP 算法可知，电磁暂态仿真过程中包含了大量的矩阵-向量点积运算。为了发挥FPGA 硬件加速的优势，通常需要使用专用硬核资源DSP48 来进行数值计算，其成为了基于FPGA 的实时仿真中的关键硬件资源和仿真规模的制约因素。本文基于状态机框架设计了一种数字信号处理（digital signal processing，DSP）资源复用的FPGA实现架构，如图4 所示，其中，PWM 表示脉宽调制。

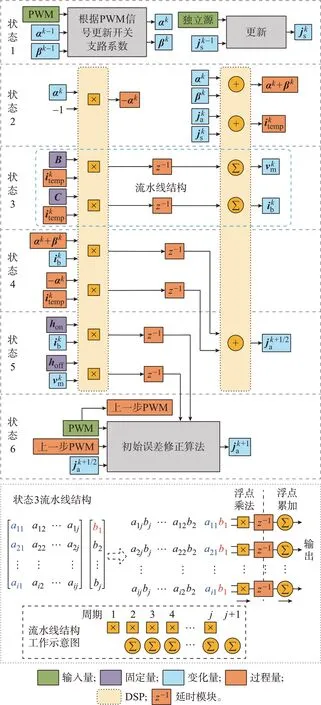
图4 基于状态机框架的DSP 资源复用FPGA 实现架构Fig.4 FPGA implementation architecture with DSP resource reuse based on state machine framework

状态1 到6 的一轮循环即为一个仿真步计算。其中，输入量为开关的驱动信号和电路中的独立源，在每个仿真步k开始时通过交互接口进入状态机中。固定量为整个仿真过程都固定不变的量，一般在仿真开始前预存储于FPGA 的随机存储器（random access memory，RAM）块中。变化量为在仿真前给定或在仿真后输出，又需要在仿真过程中不断更新的量，一般通过FPGA 的寄存器存取。过程量为仅存在于仿真过程、既不需要输入也不输出的量，也通过寄存器实现。算术运算通过调用运算IP（intellectual property）核实现，为减少通用逻辑资源消耗，提高计算速度，运算IP 核一般通过DSP48硬核资源实现。

状态机中，对角矩阵α和β采用向量的方式存储，状态机中的向量相乘即为其对应位置元素相乘，故仅需要一个周期即可完成。状态3 的矩阵向量乘法是算法的核心计算步骤，为了保证计算速度，发挥FPGA 优势，该状态需要最大化的并行度，采用文献［6］中的非对角矩阵-向量乘法流水线设计结构。由图4 可见，在点积运算的每个单元中加入一级流水线，虽然使得累加运算滞后了一个周期，整个矩阵-向量点积运算增加了一个时钟周期，但是流水线结构打断了乘法和累加的串行逻辑转为并行，缩短了最大路径延时，提高了时钟频率。累加运算可通过加法运算IP 实现。

在保证状态3 并行速度的基础上，将其他计算步骤分解后设置于其前后，与状态3 共用为其分配的乘法和加法运算IP，实现DSP48 硬件资源复用。分解后的算术运算对减法进行分步处理，节省了运算IP，仅剩下浮点数加法和乘法运算。在整个状态机中两种运算并行独立，复合运算通过流水线结构打断，用两个或更多周期实现，如式（13）中ja的更新式通过状态4 和状态5 组合实现。因此，该架构中最长逻辑路径仅为一个算术运算单元，提高了FPGA的时钟频率。

FPGA 中为提高速度一般采用定点数数据类型进行计算。然而，在电力电子系统的实时仿真中使用定点数不可避免地增加了建模难度。如各元件参数及电气量字长的选择［22］，选择不当时易增大和累积数值误差，通常需要预先离线仿真来确定各电气量的数值量级。为了获得更好的精度和降低建模难度，本文采用单精度浮点数据格式。数值计算通过NI FPGA Floating-point 库中的单精度浮点数乘法和加法运算IP 实现［23］，每个运算IP 消耗2 个DSP48和若干查找表资源，IP 核内部无流水线结构可在一个周期内输出结果。该场景下图4 各个状态需要消耗的时钟周期个数如附录A 表A2 所示。因此，在可编译的FPGA 时钟下，该架构可执行的最小仿真步长Δtmin为：

式中：Tclock为FPGA 时钟周期。本文所使用的FPGA 在50 MHz 时钟频率下进行编译，一个FPGA时钟周期为20 ns。由式（24）可知，使用性能更强大的FPGA 主芯片时，可以提高FPGA 时钟的可编译频率，进而缩短可执行的最小仿真步长。

为验证该架构的优越性，使用相同算法不同架构进行两电平VSC 的实时仿真时，资源消耗对比如附录A 图A2 所示。

在实时仿真中，DSP48 是FPGA 算数运算的珍贵硬核资源，该架构相比于无特殊设计的情况下几乎节省了一半的DSP48 资源，故能够在相同的资源数下实现更大规模的仿真运算。由于该架构是基于复用空闲资源的思想，经过图4 中合理的分解布局后，并不会因增加额外的时延而损失速度，同时还具备通用性和一定的扩展性。

4 实时仿真验证

4.1 初始误差修正算法验证

4.1.1 不同变换器的输出波形

在本文搭建的FPGA 实时仿真平台上对Boost变换器、两电平VSC［13］、三电平VSC［24］进行实时仿真验证。 采用 MATLAB/Simulink 平台中SimPower System 工具箱的相同离线仿真模型作为参考基准，其中，电力电子开关采用理想开关模型。

图5 所示是两电平VSC 在离线仿真、含修正算法的实时仿真和不含修正算法的实时仿真下的开关电压vs、电流is波形。对比图5（a）、（d）和（b）、（e）可以看出，在初始误差修正算法的作用下，实时仿真中基于恒导纳开关模型的电压和电流波形已经接近于离线仿真中理想开关的波形。需要注意的是，实时仿真中基于恒导纳开关模型已经试凑到较优的参数，但从图5（c）、（f）中可以看出，开关振荡仍然明显。

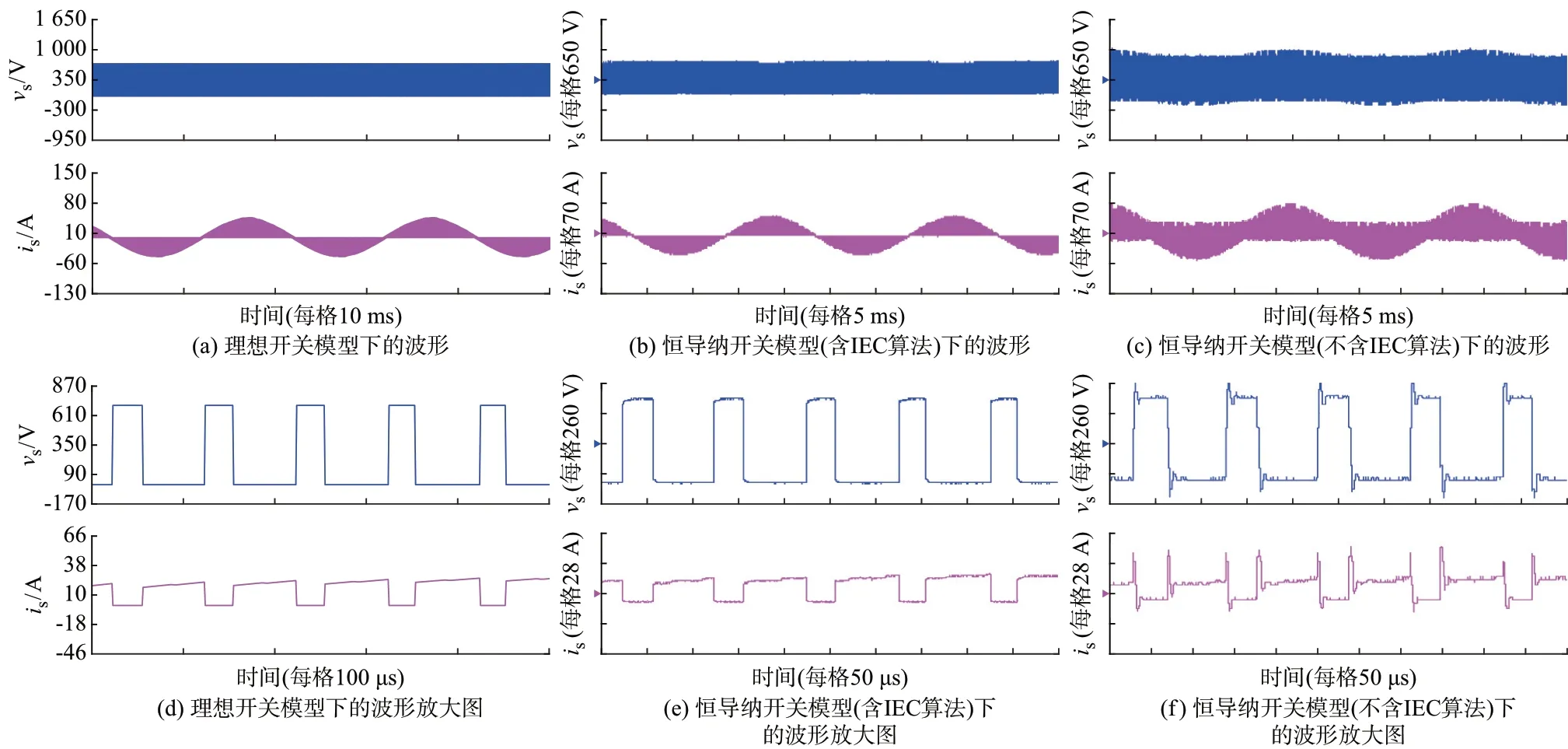
图5 两电平VSC 开关电压、电流波形Fig.5 Waveforms of switch voltage and current of two-level VSC

三电平VSC 和Boost 变换器的开关电压、电流波形如附录A 图A3 和图A4 所示，与上述所讨论的两电平VSC 相似。通过图2 桥臂模型所提出的修正算法同样适用于以Boost 变换器为例的直流斩波变换器和三电平VSC。对于任何变换器而言，电力电子开关在接通时都具有等效串联电路，在关断时具有等效并联电路，可应用于修正算法中。因此，初始误差修正算法不受拓扑结构限制，具有一定的通用性。

4.1.2 虚拟功率损耗测试和分析

图6（a）中展示了Boost 变换器、两电平VSC 和三电平VSC 在不同载波频率下的虚拟功率损耗占比。基于恒导纳开关模型的虚拟功率损耗随载波频率的增加而增加。即使选择了较优的支路导纳，它也会在高载波频率下增加到极高的水平，严重影响仿真的准确度。加入修正算法后，恒导纳开关模型已经十分接近理想开关。因此，在所有被测载波频率下，虚拟功率损耗都保持在极低的水平，基本可以忽略。在修正算法的作用下，此时的损耗更多来源于数值算法的误差。

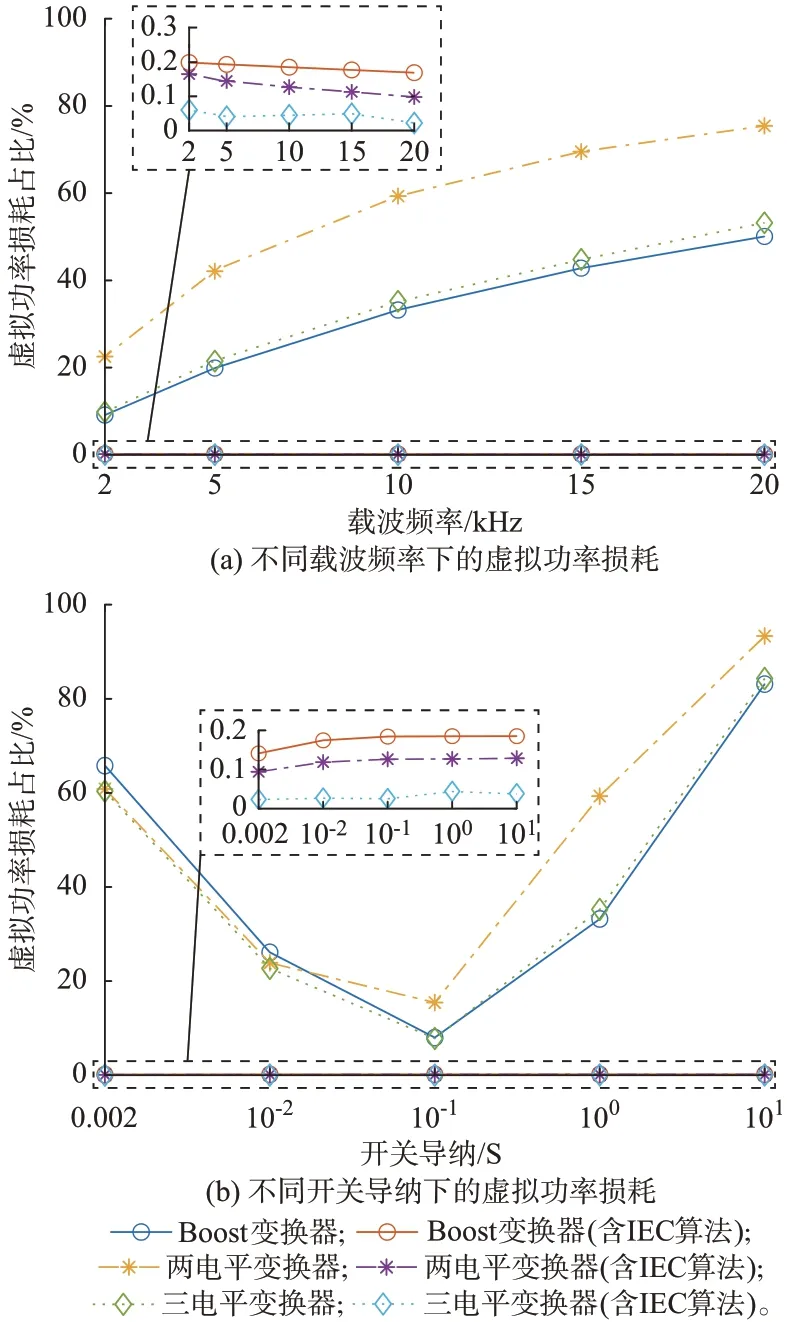
图6 不同条件下的虚拟功率损耗Fig.6 Virtual power loss under different conditions

如图6（b）所示，修正算法使得恒导纳开关模型不受支路导纳参数的影响，在较大的可选参数范围内，其虚拟功率损耗都基本可以忽略。因此，使用恒导纳开关模型时无须再进行参数的试凑优化，提高了实时仿真的建模效率。

减小仿真步长是降低恒导纳开关模型虚拟功率损耗的有效途径。然而，为了确保实时性能，所有计算必须在单个仿真步长时间内完成。因此，最小仿真步长受到FPGA 硬件资源瓶颈的限制，不能无限减小。表2 给出了不同仿真步长下的虚拟功率损耗占比。结果显示，从小步长到大步长，引入修正算法后的虚拟功率损耗都几乎为零。因此，修正算法不受仿真步长的影响，即使在较大的步长下也能够保证其有效性，可以减小硬件负担。

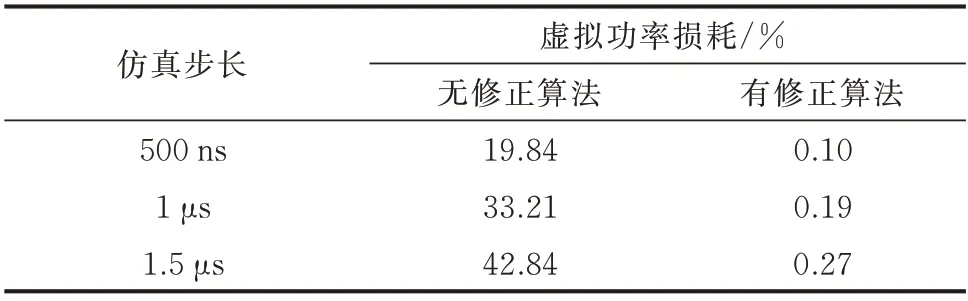
表2 不同步长下的虚拟功率损耗占比Table 2 Percentage of virtual power loss with different step sizes

IEC 算法由于从数值算法本身出发，通过数值修正的方式使开关切换过程更加贴近理想开关，能从根源上消除功率损耗。该算法不受拓扑、模型参数和仿真步长的限制，具有普适性。同时，该算法流程简单高效，在基于状态机框架的DSP 资源复用FPGA 架构下，仅增加了图4 中状态6 的一个时钟周期。从表3 可知，修正算法的加入不会增加额外的DSP48 资源的消耗，仅因额外的逻辑判断增加了少量的查找表资源。

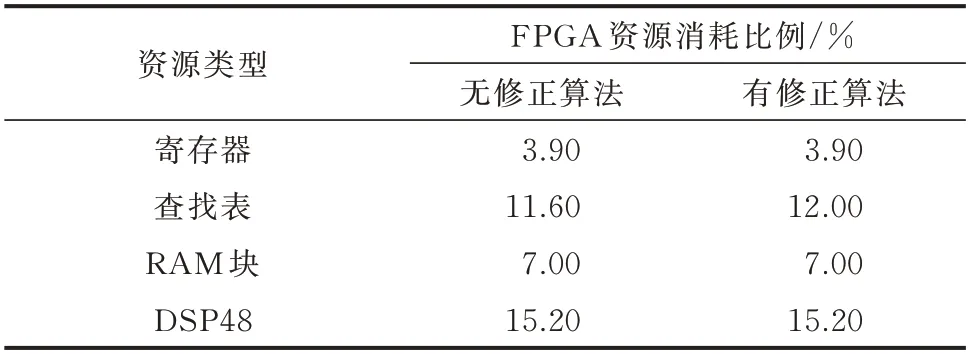
表3 两电平VSC 实时仿真中有无修正算法的FPGA资源消耗比例Table 3 FPGA resource consumption ratio with and without correction algorithm in real-time simulation of two-level VSC

4.2 混合微电网算例验证

如附录A 图A5 所示，本文搭建了一个含互联变流器（interlinking converter，IC）的交直流混合微电网系统，系统采用文献［25］的模型参数和控制方法，主要参数如附录A 表A3 所示。

本文在所开发的FPGA 实时仿真平台中实现了以上系统的自闭环实时仿真，其中，FPGA 中控制系统的实现参考文献［17］中的方法。同时，基于Simulink/SimPowerSystem 平台搭建了相同的离线仿真模型作为参考基准。该系统能够在本文的FPGA 实时仿真平台中实现1 μs 步长的时域仿真。

如附录A 图A6 所示，互联变流器的目标是均衡两侧子网的功率，使两侧子网共同分担负荷，实时仿真结果显示在所设定工况下均能实现控制目标，与实际结果相符。图A7 给出了该系统中直流母线电压、交流母线电压和互联变流器传输电流的输出波形，结果均与离线参考值基本吻合。

该混合微电网算例的实时仿真结果表明IEC 算法和基于状态机框架的DSP 资源复用FPGA 架构能够保证电磁暂态实时仿真结果的正确性。

5 结语

针对电力电子实时仿真领域中的3 个技术点和问题，本文逐一分析并进行改进，主要工作和结论如下：

1）推导了简洁EMTP 算法，将传统EMTP 算法解耦压缩，提高了算法的并行度。在FPGA 实现上采用浮点数据格式，免去了文献［6］中的Compact EMTP 算法因定点数的数值差异进行的混合建模过程。同时，将用户的观测需求合并到算法过程中，舍弃非必要的输出量，FPGA 实现时无须因测量元件增加额外的步骤和资源消耗，提高了算法的计算效率和简洁性。

2）从数值算法的角度分析虚拟功率损耗的来源，得出其主要原因在于恒导纳开关模型在开关切换时刻产生的初始误差。提出了一种初始误差修正算法，可以基本消除由开关模型引入的功率损耗。该算法具有普适性，可应用于多种拓扑且不受仿真步长和模型参数的影响。

3）自主搭建了一套基于FPGA 的电力电子仿真平台，在考虑FPGA 的硬件特性基础上进行本文算法的实现，提出了一种基于状态机框架的DSP 资源复用FPGA 架构。该架构可以提高FPGA 资源的利用效率，同时减小加入IEC 算法对硬件资源消耗的影响。

综上，本文解决了基于FPGA 的电力电子系统实时仿真中的虚拟功率损耗问题，提高了硬件资源利用效率。随着微电网规模和容量的增加，需要仿真和测试的电力电子系统规模也随之扩大。针对更大规模电力电子系统的实时仿真算法优化方法和FPGA 架构是下一阶段研究的重点方向。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。