地铁下穿上盖高层建筑振动响应预测与分析

谢艳花,黄子贶,郑钰钰,徐 敏,李建宏,楼煌杰,叶 昕,袁宗浩

(1.中国联合工程有限公司,浙江 杭州 310052;2.浙江工业大学 土木工程学院,浙江 杭州 310023)

截至2021年底,国内有50座城市投运轨道交通,线路长度共计9 192.62 km[1]。为了提高城市土地利用率,将地铁车站上部空间利用起来是最直接有效的方法,同时也可以促进商业和交通的发展。由于振源距离较近,地下交通引起的振动和噪声对人们生活环境和身体以及车站、上盖建筑的影响是不可忽视的[2-3]。国内外已有很多学者针对地铁列车运营引起的环境振动问题展开了相关研究。孙宇等[4]基于格林函数和轮轨Hertz非线性接触理论,提出了求解车辆-轨道垂向耦合动力学的新方法,同时证明格林函数法在车辆-轨道耦合动力学计算中的可靠性;王国才等[5]基于饱和土波动方程,通过Hankel变换导出了在简谐集中扭矩作用下饱和半空间表面问题的积分形式解,分析了半空间表面应力和位移随振源距离的变化规律,并研究了土体参数和激振频率对饱和地基土动力响应的影响;王哲等[6]利用Attewell分析公式,研究了隧道的半径、隧道的埋深和土质对浅埋暗挖法隧道施工引起的沉降槽宽度系数值的影响,并提出了一种更加适用于杭州软土地区的分析公式;Sheng等[7]利用解析法研究了列车荷载传播在地表处的共振现象,分析钢轨结构、车速等不同因素对振动传播的影响。然而上述研究理论计算步骤繁琐、简化假定条件多,可适用的工况范围也受到了很大的限制,而数值计算法应用范围更广。王逢朝等[8]通过建立车辆-结构-土层-建筑物的二维模型,研究了不同隧道埋深和建筑层数下地铁列车振动对邻近建筑物的影响;关天伟等[9]利用Plaxis3D有限元软件建立列车-隧道-土体-上部结构三维模型,研究地铁车辆运行对周围土体和建筑的影响车辆耦合。由于缺少必要的测试条件,针对尚处于规划中的地铁线路,不能够像多数已施工完成的建筑或车站一样采用纯实测[10]方式完成环境振动评价。由于实际环境振动问题的复杂性,考虑土层非均质、钢轨不平顺等随机因素,单采用数值模型[11]无法准确分析环境振动问题,因此采用振动实测与数值模拟相结合的方式对规划中的地铁线路开展环境振动评价是非常重要的方法。谢伟平等[12]等结合工况实测数据,建立精细化有限元模型,计算分析上盖高层建筑的振动响应,分析列车进出车辆段处上盖建筑振动传播规律;郑玄东等[13]建立了莘庄枢纽车站半空间一体化有限元模型,结合莘庄站现场实测数据求得轮轨荷载,分析模拟了沪杭客专运行时增设隔振基础下邻近建筑的振动响应;包碧玉等[14]以某新建地铁下穿复合地基高层办公楼建筑为背景,结合北京地铁隧道处实测数据,建立数值模型以验证模型的有效性,最后建立三维有限元预测模型,分析评价不同浮置板道床下的振动响应。

目前,针对拟建地铁车站附近的超高层建筑振动响应规律与评价方面的研究相对较少,相较于低层建筑来说,高层或超高层建筑存在建造时间长、投入成本高、外界因素干扰大和楼板跨度大等不利因素,且受到环境振动影响因素也更复杂,同时地铁车站附近拟建高层建筑振动的传播与衰减规律尚不明确。对地铁车站附近上盖建筑振动舒适度评价是十分必要的,超前振动评价可避免后期投入大量成本以解决振动超标问题。因此,笔者提出一种适用于下穿地铁车致高层建筑振动响应计算反分析法,首先采用ABAQUS有限元分析软件建立车-轨-隧道-土体-建筑耦合振动数值模型,通过自编程Fortran程序,编写列车荷载施加、求解和时程分析的一体化计算过程,调用VDLOAD子程序实现有限元模型中变幅值移动性动荷载的输入、模拟和计算结果输出,通过对比杭州某地铁车站新建上盖建筑振动实测结果与计算结果,验证了笔者方法的有效性;然后将其应用于车站处拟建上盖建筑,研究邻近列车荷载对拟建超高层上盖建筑的振动影响,分析地铁振动在建筑中的传播规律,完成对拟建建筑振动响应的预测评价。

1 研究方法

1.1 列车移动荷载模拟

为了研究地铁列车振动波在车站邻近高层建筑中的振动传播规律,在有限元模型计算时,借用ABAQUS计算模型调用VDLOAD子程序,通过自编程Fortran程序,完成列车荷载施加、求解和时程分析的一体化计算。变幅值的移动荷载可通过调整随时间变化的荷载幅值、作用位置来实现不同类型列车荷载的加载与模拟[15]。

列车移动荷载可简化为由一系列不同幅值正弦力组合而成的竖向动荷载[15],列车移动荷载模拟计算式为

(1)

式中:F(t)为t时刻车轮平均力;w为每个车轮的重量;θi为相位差;φ(i)为不同频率i下正弦力幅值调整系数;n为振动频率的个数。

列车车轮位置确定公式为

xm(t)=xm,0+Vt

(2)

式中:xm(t)为在t时刻列车移动至第m个车轮距离最初零坐标沿列车移动方向的位置坐标;xm,0为第m个车轮距离零坐标的位置;V为列车前进速度。

结合车辆几何参数值,通过式(1)确定位于单一轮轴下初始位置的轮轨间作用力,由于此处列车荷载为集中力,且列车由多节车厢的多个轮轴构成,需通过式(2)确定列车运行时车轮相对于初始位置的相对距离,并进一步确定模型中列车荷载具体施加位置点坐标,从而实现列车运行状态下移动荷载的模拟。

由于式(1)中将轮轨间作用力虚拟为一系列简谐荷载的叠加形式,因此在采用有限元开展建模时,可以忽略车体部分,避免求解复杂的车体-轨道系统,轮-轨的作用力可通过现场振动实测数据反分析获得。

1.2 有限元反分析法

基于上述列车移动荷载模拟方法,图1给出了反分析预测分析方法的技术路线图,该方法可将上盖建筑振动现场测试与有限元数值模拟相结合。由于该上盖建筑为拟建项目,没有现场振动实测条件,故选取杭州地铁线某相似区间段,开展上盖建筑现场振动测试与数值模拟。首先,建立相似工况下的“振源-车站-土”精细化有限元数值模型,将相似工况下实测振动响应与模型试运算结果进行对比,依据两者间的差异将式(1)中轮轨间作用力参数进行调整优化,即不断调整虚拟力的幅值和相位,经过多次模型试运算和荷载参数优化,直至两者吻合结果较好,以确定虚拟力的大小,同时验证了有限元反分析模型的有效性;然后,建立拟建项目“振源-车站-土”有限元模型,输入已确定的相似工况下的虚拟力,预测分析地铁车致高层建筑振动响应数值。

图1 反分析预测分析方法技术路线图Fig.1 Technology road map for back analysis prediction method

2 有限元模型验证

选取与待研究地铁上盖建筑相似的工况开展地铁线邻近建筑振动的现场实测工作,同时建立相似工况下列车-车站-土体-上盖建筑数值模型,并与实测数据进行对比分析,以验证下穿地铁车致高层建筑振动响应计算反分析法的正确性。

2.1 测试工况

测试地点位于杭州地铁4号线某车站处新建上盖建筑工程,地铁线路与建筑位置关系如图2所示。地上建筑为16层,地下室为3层,均为剪力墙结构。地铁4号线下穿此地块。地铁4号线由一条单线隧道组成,运行列车为6节编组B型车,运营速度为80 km/h。地铁4号线穿越振动测试地块,建筑结构位于地铁车站上部,地下室与车站相连,选取建筑共有17层,地下车站3层,列车在地下3层运行。

图2 列车-建筑位置关系图Fig.2 Relative positions of underground metro lines and buildings

采用INV3062C信号采集仪,每个位置均布置加速度传感器,柱测点采集Z向的振动加速度,板位置测点采集X,Y,Z3个正交方向的振动加速度,采样频率为512 Hz,每次采样时间为30 min。结合实际工程需要,选择邻近地铁线路处柱、板等结构构件进行连续观测,每层测试为5个柱测点和2个板测点,测试位置如图3所示。本项目振动环境测试主要依据规范中振动测试的相关规定进行。具体方法如下:在进行现场测试时,选用快干胶将拾振传感器分别粘在地面测点和柱测点处,板测点处放置竖向和水平向传感器,柱测点上放置竖向传感器,再通过信号线将INV3062C信号采集仪和计算机连接起来进行信号收集。

图3 测点位置图Fig.3 Location of measurement points

2.2 数值模型验证

由于待研究目标处于规划中,目前不具备测试条件,故选取相似车站结构及上盖建筑项目进行现场振动测试,同时建立土体-车站-上盖建筑有限元分析模型,计算列车运行引起的建筑振动,同时与实测结果进行对比分析。

结合2.1节对选取近似工况的概述,建立如图4所示的土体-车站-列车有限元模型,计算列车运行地铁车站地下1层的振动响应。该工况(地铁4号线)已建车站共计3层,列车荷载在地下3层运行;柱采用C40混凝土,横截面积为700 mm×1 100 mm,沿轨道方向的柱间距为8 m,梁、板、墙采用C30混凝土,纵梁截面为600 mm×900 mm,上述构件均采用实体单元模拟。

图4 列车-车站有限元模型Fig.4 Track-station finite element model

建立有限元验证模型后,结合地铁4号线运营列车参数信息,用一系列不同幅值正弦力组合而成的竖向动荷载模拟列车荷载。以地下1层柱点位实测数据为参考,开展振源虚拟力的反分析,通过对模型中输入荷载幅值和相位的不断修正,最终确定模型中振源力的大小,并将该振源力激励下的响应计算结果与相同点位的实测结果进行对比,结果如图5所示。

图5 模拟数据与实测数据Fig.5 Comparison between simulations and field measurements

由图5可知:现场振动测试与有限元模型计算的结果曲线规律和量级总体上保持一致,验证了利用有限元模型分析振动响应的有效性,该模拟过程运用了反分析法确定振源,由于待研究工程和实测工程的工况一致,该振源可同时作为预测拟建项目振动响应的虚拟振源力。

3 数值预测结果分析

3.1 计算模型

建立地铁6号线拟建车站及上盖建筑有限元模型,车站共计5层,列车荷载在地下5层运行;计算模型中梁、柱、板、墙的几何尺寸均按实际情况建立,柱采用C50混凝土材料,梁、板、墙采用C35混凝土材料,上述构件均采用实体单元模拟,沿轨道方向的柱间距为9 m,车站每层均布置纵梁,顶层增加布置横梁。由于振动实测项目(4号线)与待研究项目(6号线)在地铁车辆类型、轨道类型和地层条件等方面均具有较好的一致性,因此在对拟建地铁6号线项目附近高层建筑进行振动预测时,选择了与4号线相同的虚拟力源进行预测分析。同时,根据实际拟建上部建筑结构参数信息,建立如图6所示的列车-车站-土体-上盖建筑精细化三维有限元模型。

图6 列车-车站-土体-上盖建筑三维有限元模型Fig.6 Track-station-soil-building 3D finite element model

计算土体模型尺寸为150 m×160 m×80 m,考虑到实际土体结构的复杂性,将土层简化为4层,各层土厚依次为7,17,19,37 m,具体土层参数如表1所示。车站结构为地下5层,板和梁采用C35混凝土材料,柱采用C50混凝土材料,车站3～5层板厚为500 mm,车站2层板厚为700 mm,车站顶部距离地表1.2 m,整体宽度为54.0 m,高度为57.2 m。建筑中楼板和梁部件采用C35混凝土材料,建筑不同楼层范围的剪力墙、楼柱部件选取的混凝土材料有所不同,C30～C60混凝土材料的参数如表2所示。上盖建筑总层高为32层,总体高度为126.3 m,建筑各层板厚为150 mm。整体模型网格尺寸划分为1 m/个,为了提高计算效率,远离振源处网格选择3 m/个,共计1 199 113个单元。计算模型边界采用无限元边界,避免振动传播至有限元模型截断处的反射影响计算结果。

表1 土层参数

表2 建筑部件参数

3.2 上盖建筑振动预测结果分析

3.2.1 建筑振动整体响应分析

各楼层过车响应峰值如表3所示,列车过车总时长为10 s,时域中最大加速度在过车中间时段,1～32层最大加速度峰值为0.62～4.22 mm/s2,频谱中幅值峰值主要出现在低频10～20 Hz和高频50～80 Hz处,低频峰值为0.07～0.22 mm/s以及高频峰值为0.046～0.580 mm/s。地铁列车运行建筑结构各楼层柱测点振动加速度时程如图7所示。由图7可知:各楼层加速度时程图是明显过车曲线,呈梭形分布。地铁列车运行建筑结构各楼层柱测点振动幅值频程图如图8所示。当地铁列车过车时,上盖建筑内最大振动分布于10～80 Hz。随着建筑楼层的增加,振动幅值总体呈现逐渐减小的趋势,在顶层有放大现象,这是由于在建筑顶层存在振动波反射情况,波动传递导致的叠加反射效应使顶部出现振动放大区;当振动幅值在20 Hz之内时,随着楼层的增加没有明显变化,甚至出现部分增大现象,这是由于低频范围内波长较长,沿着楼层高度方向衰减有限,而振动幅值在20 Hz以上时波动减小趋势明显,这是由于高频成分波长较短,沿楼层高度方向衰减明显。图8中的频谱结果表明:建筑振动沿高度方向以传播低频振动为主,楼层结构对高频成分有一定的过滤作用。

表3 各楼层过车响应峰值

图7 建筑振动加速度时程图Fig.7 Time-history spectra of building vibration acceleration

图8 建筑振动加速度频程图Fig.8 Amplitude frequency spectra of building vibration acceleration

最大Z振级随楼层的变化关系如图9所示。由图9可知:列车过车时柱的最大Z振级随着楼层的升高总体呈现先减小后增大的趋势,最大振动响应位于第5层,最大值为51.1 dB;在5～15层衰减率约为0.6 dB/层,15～21层曲线平缓无明显衰减变化,在22～25层衰减率约为0.94 dB/层,在25～32层高层处,振动响应呈现放大情况,放大率约为0.93 dB/层,这是由于振动传播至顶层时经过波的反射,故顶部楼层响应明显变大。

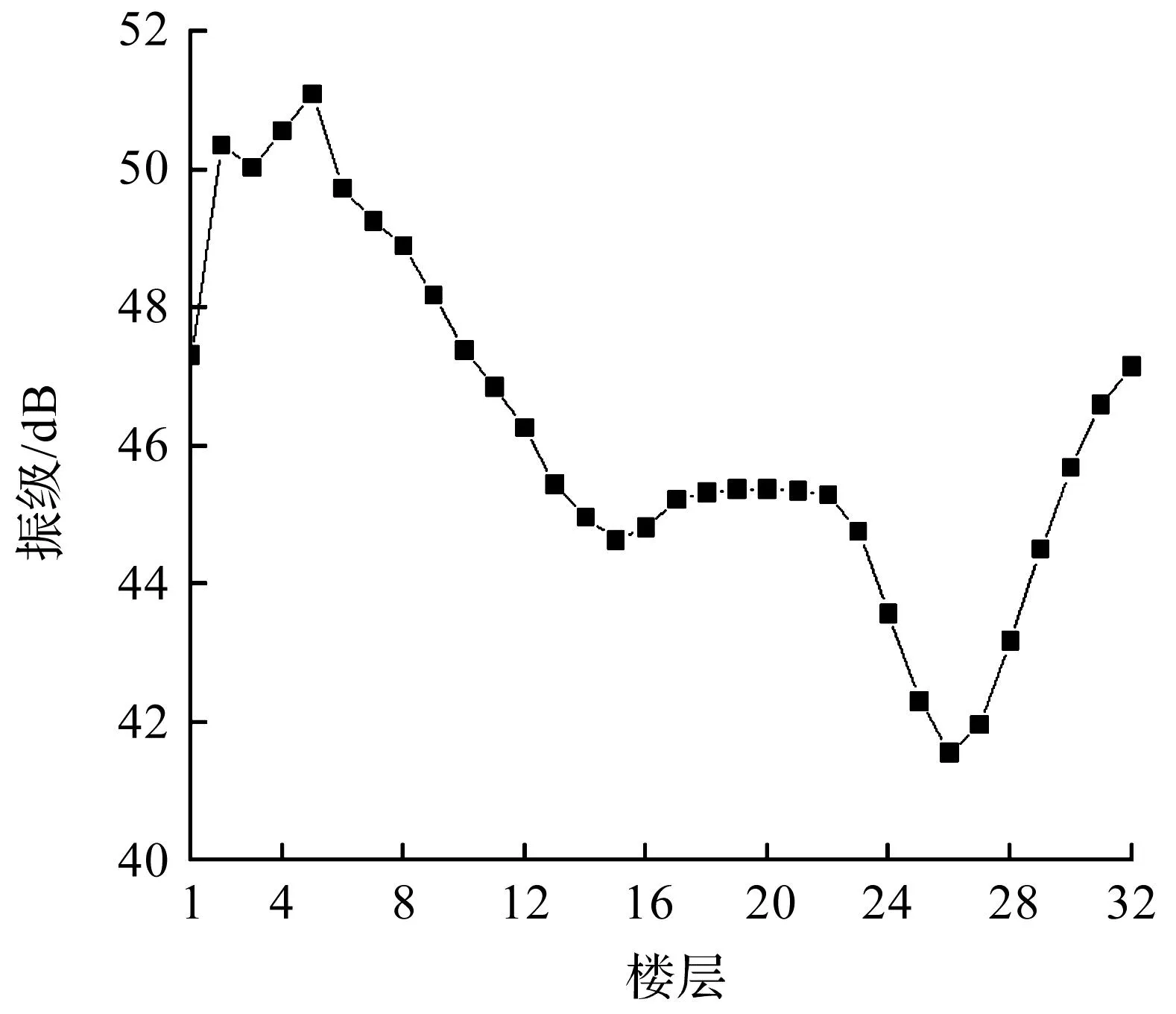
图9 最大Z振级随楼层变化图Fig.9 The change of Z vibration level on different floors

不同楼层柱测点的1/3倍频程图如图10所示。由图10可知:1/3倍频程的最大振级随着楼层的增加先减小后增大,建筑内各楼层内最大振动分布为63 Hz,分频程振级1层最大,振级为58.18 dB,该频率对应车体—轨道体系的共振频率,由于该频率下的轮轨动力作用力为最大,各楼层的分频响应均在此频率下取得了最大值。如图8所示,随着楼层增加,低频振级变化差异较小,而在高频处振级衰减趋势明显。

图10 柱测点1/3倍频程图Fig.10 1/3 octave frequency response at the column points

3.2.2 总建筑楼层高度对建筑振动响应的影响

由于地铁振动波在建筑中传递规律主要取决于建筑结构的刚度,而建筑结构的整体刚度随着总建筑楼层高度会发生显著变化,因此总建筑楼层高度可对振动传播规律产生重要影响。为了探究总建筑楼层高度变化对地铁振动响应的影响规律,建立不同楼层高度的建筑模型,对比分析相同位置处建筑振动响应的变化规律。如图9所示,选择在整体建筑Z振级响应图中存在转折变化的临界楼层作为总建筑楼层层高,因此总建筑楼层层高分别为1,5,15,25,32层,得到不同总建筑楼层下同一层1/3倍频程图对比图,楼层结果分别如图11(a～d)所示。

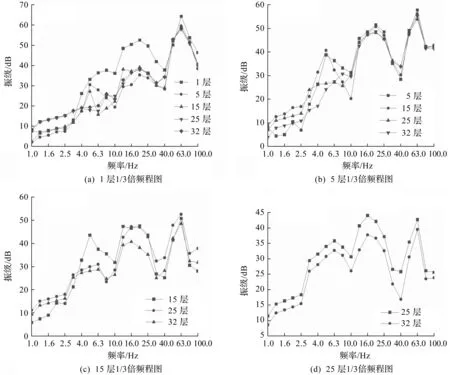
图11 各楼层柱测点1/3倍频程图Fig.11 Vibration acceleration in 1/3 octave band frequency at columns for buildings with various total floors

由图11可知:随着建筑总楼层的增加,1/3倍频程振级变化趋势总体一致,振动最大响应频率分布在63 Hz,以频率为63 Hz时各1/3倍频程图振级为例,随着楼层总层数的增加,即建筑楼层从1层增加至5,15,25,32层时,可以从图11(a)中看到1层振级分别减少了4.80,4.96,6.40,6.16 dB;建筑楼层从5层增加至15,25,32层时,从图11(b)中看到5层振级分别减少了1.6,3.9,2.5 dB;建筑楼层从15层增加至25,32层时,从图11(c)中看到15层振级分别增加了1.5 dB和减少了2.2 dB;建筑楼层从25层增加至32层时,从图11(d)中看到振级减少了3.2 dB。因此,同一层振级随着总建筑楼层高度的增加,柱位置响应振级伴有幅值衰减;在低于40 Hz低频部分,同一楼层1/3倍频程振级变化较大,变化最大差值为6.37 dB,而高频处变化则相对较小,这是由于随着建筑总楼层的增加,建筑整体总刚度增加,而刚度的变化对低频部分振动有较大影响,因此可以看到当总建筑楼层发生变化时,位于同一楼层的振动响应在低频部分差异明显,然而由于波沿着楼层高度方向传播时,不同建筑楼层内振动响应处于波峰和波谷的不同位置,因此刚度的增加与低频响应的减小不具有线性关系,刚度一致性并不明显。

总建筑楼层高度对Z振级响应的影响如图12所示。随着总楼层的增加,最大Z振级总体上逐渐减小,当建筑总楼层由1层增加到5,15,25,32层时,1层最大Z振级分别减少了7.34,7.56,7.79,7.57 dB;当建筑总楼层从5层增加到15,25,32层时,5层最大Z振级分别减少了0.48,2.06,1.68 dB;当建筑总楼层从15层增加到25,32层时,15层最大Z振级分别减少了2.82,8.11 dB;当建筑总楼层从25层增加到32层时,25层最大Z振级损失了3.65 dB。可以看出楼层的高度会对建筑物的振动产生一定影响,随着建筑楼层升高,低楼层响应变化比高楼层的振动响应变化明显。

图12 总建筑楼层对Z振级的影响Fig.12 Change of Z vibration level for building vibration with various total floors

4 结 论

在地铁车站附近修建高层建筑和大型综合体虽然解决了用地问题,给居民带来了生活便利,但地铁产生的振动和噪声问题突出。为了快速有效地评价振动响应水平,提出了一种适用于下穿地铁车致高层建筑振动响应计算反分析法,开展地铁线邻近建筑振动的现场实测工作,同时建立拟建项目列车-车站-土体-上盖建筑数值模型,将数值模拟结果与实测结果进行对比分析,验证反分析法的正确性。利用该反分析数值模型,分析了地铁车站附近上盖高层建筑的振动传播与衰减规律,研究结果表明:上盖建筑的振动响应随着楼层的升高总体呈逐渐减小的规律,在楼层顶部有增大现象;随着建筑楼层升高,20 Hz以上高频的响应逐渐减小,20 Hz之内低频响应无明显变化;随着楼层的升高,不同楼层相同平面位置处最大Z振级总体呈现先减小后增大的趋势;在5～15层衰减率约为0.6 dB/层,在15～21层振动无明显衰减变化,在22～25层衰减率约为0.94 dB/层,在25～32层高层处振动响应出现放大情况,放大率约为0.93 dB/层;随着建筑整体楼层高度的增加,低楼层的振动响应变化比高楼层明显,特别是对于低频建筑振动响应。