考虑管线老化和破损时基坑开挖对邻近管线纵向变形的影响
2024-01-18郭丙来章丽莎
魏 纲,郭丙来,王 哲,章丽莎
(1.浙大城市学院 土木工程系,浙江 杭州 310015;2.浙江省城市盾构隧道安全建造与智能养护重点实验室,浙江 杭州 310015;3.城市基础设施智能化浙江省工程研究中心,浙江 杭州 310015;4.浙江工业大学 岩土工程研究所,浙江 杭州 310023)
近些年,城市建设不断推进,随之而来的是基坑工程的增加,基坑开挖对周边环境的影响问题引起了学者的广泛关注[1-2]。而城市中电力管线、通讯线缆和燃气管道等地下管线分布密集,一旦遭到破坏,后果不堪设想。因此有必要针对邻近基坑的地下管线变形进行研究。
邻近基坑地下管线变形研究方法主要有:实测分析[3-4]、理论解[5-8]、有限元模拟[9]和模型试验[10]。理论解方面,李大勇等[5]基于Winkler地基,以抛物线形式拟合地下管线处土体水平以及竖向位移曲线,推导了邻近基坑的管线竖向以及水平变形解;张陈蓉等[6]提出了坑外土体沉降以及围护墙水平位移变形预测曲线,基于位移控制法得到了基坑开挖引起的地下管线位移以及内力;刘红岩等[11]在李大勇等的基础上,以实测地表位移替代拟合抛物线,进一步验证了弹性地基梁法求解地下管线竖向位移的正确性;苏骏等[12]基于监测数据提出了邻近基坑的管线位移函数。现有的研究大多先要计算出基坑开挖导致的地表沉降以及围护结构变形,然后再计算邻近地下管线的竖向以及水平位移,计算步骤繁琐,需要进一步研究,同时地下管线在使用过程中可能发生老化和破损[13],目前未见考虑管线老化和破损因素的相关研究。影像源法[14]由于能够充分利用现场监测数据,因此可精确地计算由于土体损失引起的土体位移,近年来在盾构掘进、基坑开挖引起的土体变形计算研究中得到了广泛应用。卢海林等[15]应用影像源法得到盾构掘进引起的土体变形;徐日庆等[16]在影像源法的基础上,考虑了土体收敛非均匀性,得到基坑开挖引起的土体水平位移。部分学者进一步考虑了施工活动引起的土体变形对邻近构筑物的影响。张爱军等[17]基于两阶段分析法,提出基于影像源法的基坑开挖对邻近桩基影响的计算方法;张治国等[18]进一步考虑Kerr地基模型,更精确地分析基坑开挖对邻近桩基的影响。基于影像源法可同时计算土体损失引起的任意点的竖向以及水平位移,完美解决了目前基坑开挖引起邻近地下管线变形计算流程繁琐的问题。笔者考虑基坑围护结构变形以及管线老化破损的影响,提出基于影像源法的基坑开挖引起的邻近地下管线变形计算方法,并对基坑围护结构变形控制参数、管线埋深、管线轴线到基坑围护结构的水平距离、管线使用年限和管线破损程度这5个影响因素进行了分析。
1 力学模型建立及公式推导
1.1 现有模型的不足之处
针对计算流程,对现有基坑开挖对邻近地下管线影响的理论研究方法进行了归纳,结果如表1所示。
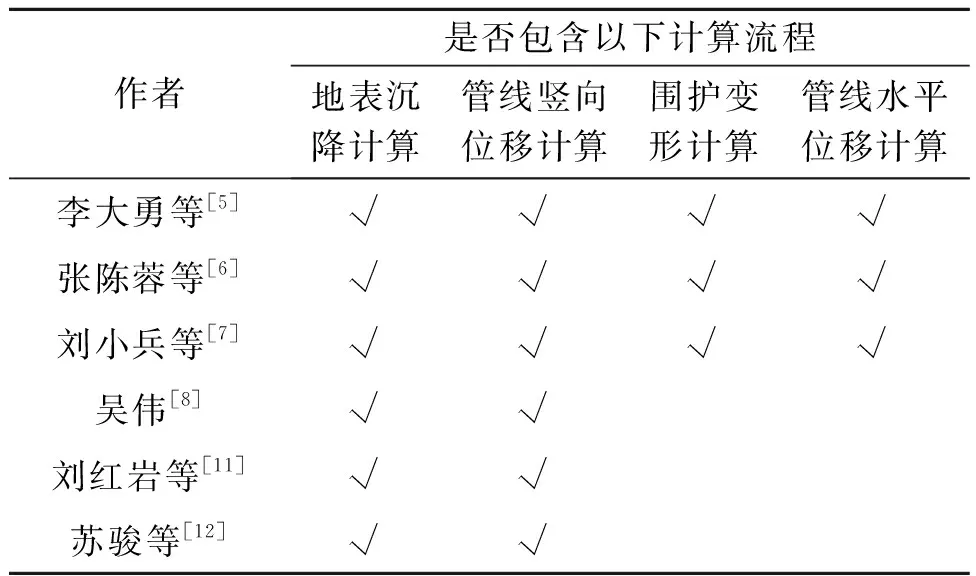
表1 理论解方法
目前理论解方法存在以下不足:1) 通过基坑开挖引起的地表沉降仅能得到邻近地下管线的竖向位移(表1),为了计算地下管线的水平位移,则需要进一步计算基坑开挖引起的围护结构变形,无法仅通过地表沉降或围护结构变形得到邻近基坑地下管线的竖向以及水平位移;2) 在管线埋设之后,管线强度会随着使用年限的增加而逐渐减小,且管线可能受外力因素产生部分破损,从而受扰动时变形更大,然而目前未见考虑上述因素的理论研究。
1.2 针对不足之处的改进
笔者建立了基坑围护结构变形预测模型,基于影像源法,通过基坑围护结构变形可同时得到基坑开挖引起的邻近地下管线竖向以及水平位移,解决了目前理论解计算流程繁琐的问题。以管线整体刚度折减考虑老化因素,以管线部分位置刚度折减考虑管线破损因素,提供了一种考虑老化和破损因素的邻近基坑地下管线变形计算方法。
1.3 建立力学模型
如图1所示,基坑开挖尺寸为L×B,挖深为d,围护结构深度为H。以基坑开挖中心为坐标原点,x为基坑开挖宽度方向,y为基坑开挖长度方向,z以向下为正;管线轴线与基坑侧壁距离为s,埋深为h,管线外径为D。
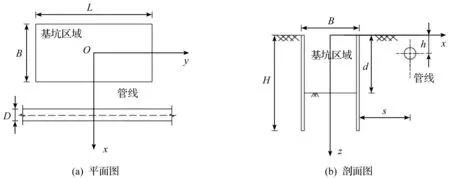
图1 基坑与邻近管线相对位置示意图Fig.1 Relative position of foundation pit and pipeline
1.4 基坑侧壁变形预测模型
建立一种适用于内撑式支撑体系的基坑侧壁变形预测模型。基坑开挖过程中侧壁变形示意图如图2所示。图2中:η为侧壁上一点的深度;λ为侧壁上一点距较近基坑边角的距离;深度为η处发生的变形为v(η)。
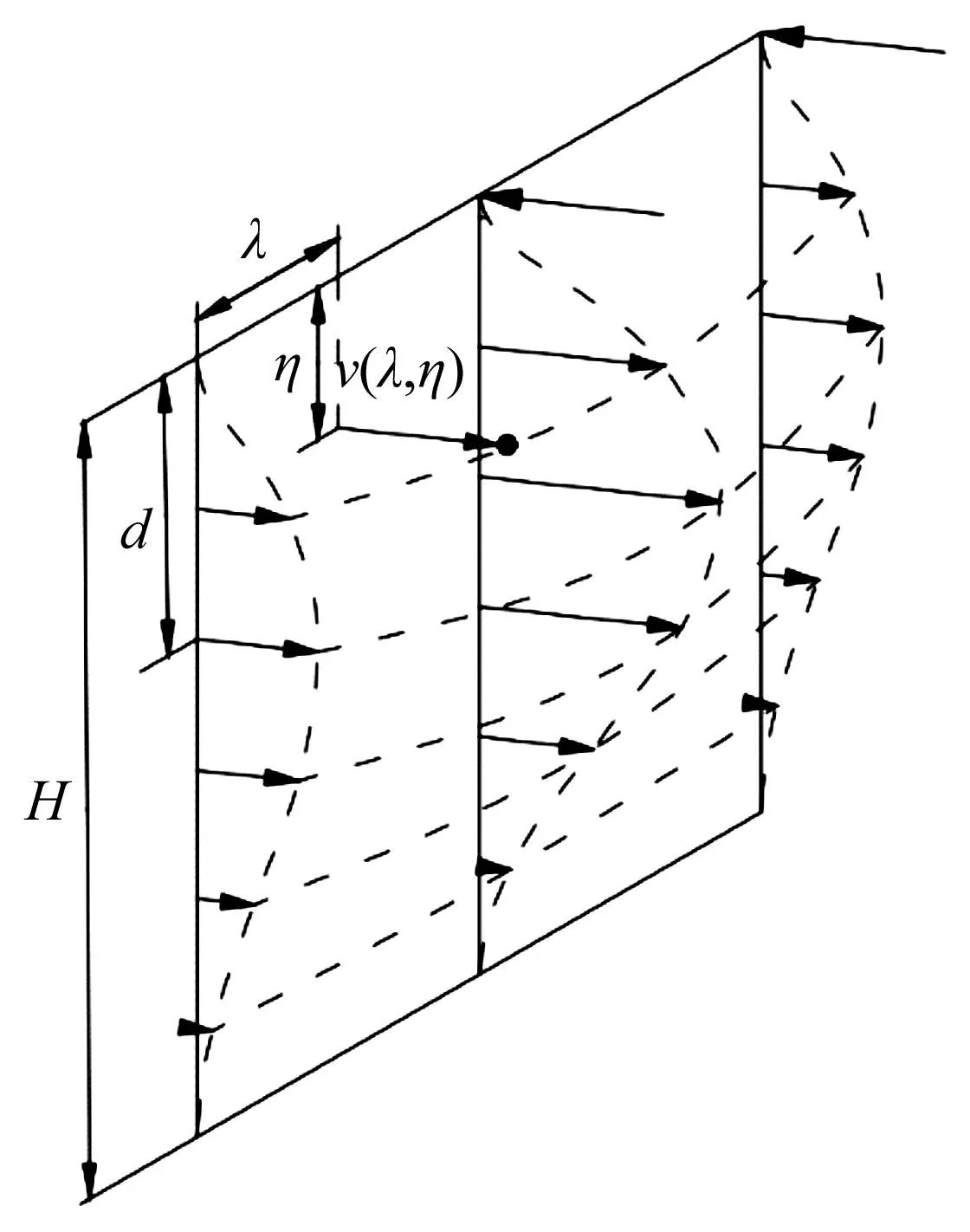
图2 基坑侧壁变形示意图Fig.2 Deformation diagram of sidewall
刘美麟等[19]以分段余弦函数拟合围护结构变形增量,围护结构变形增量最大值位于开挖面附近,变形增量为
(1)
式中:vi(η,di)为第i层开挖引起η深度处围护结构的变形值;vmaxi为第i层开挖引起的围护结构最大变形值;di为第i层的开挖面深度。
参考Zhang等[20]的研究,以基坑侧壁的累计最大变形与挖深之比vmax/d作为侧壁变形控制参数,每次开挖围护结构变形都满足控制参数,则第i层开挖引起的侧壁最大变形为
(2)
基坑开挖过程中侧壁变形会呈现明显的空间效应,围护结构中部位置变形较大,基坑边角处则较小。Ou等[21]引入了平面应变比PSR(在三维模拟条件下,围护结构的位移与平面应变条件下围护结构位移的比值)定量描述基坑空间效应。刘念武等[22]发现采用地下连续墙围护结构的PSR变化趋势与Finno等[23]提出的拟合公式曲线类似,边角附近处PSR为0.72,当PSR接近1.00时,对应的λ/d为4.00,代入拟合公式可得
(3)
整合式(1~3)可获得考虑空间效应后基坑每层开挖时侧壁任一点变形增量计算公式,即
ϑi(λ,η,di)=PSR(λ,di)·δi(η,di)
(4)
当基坑开挖m层,坑底深度为di时,侧壁的位移为
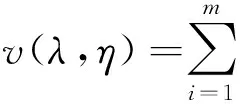
(5)
1.5 管线轴线处土体位移计算
Sagaseta[14]提出影像源法,得到弹性半空间中任意点地层损失引起的周围土体位移场。基于该方法,对土体位移作了一定假设:1) 土体不可压缩,土体损失是导致土体变形的原因;2) 忽略土体固结、流变以及孔隙水压力等影响。
在如图3所示的直角坐标系中,邻近管线侧壁上一点(B/2,y,z)半径为a的间隙在管线轴线上的点(x1,y1,z1)处产生的位移沿z轴分量为
(6)
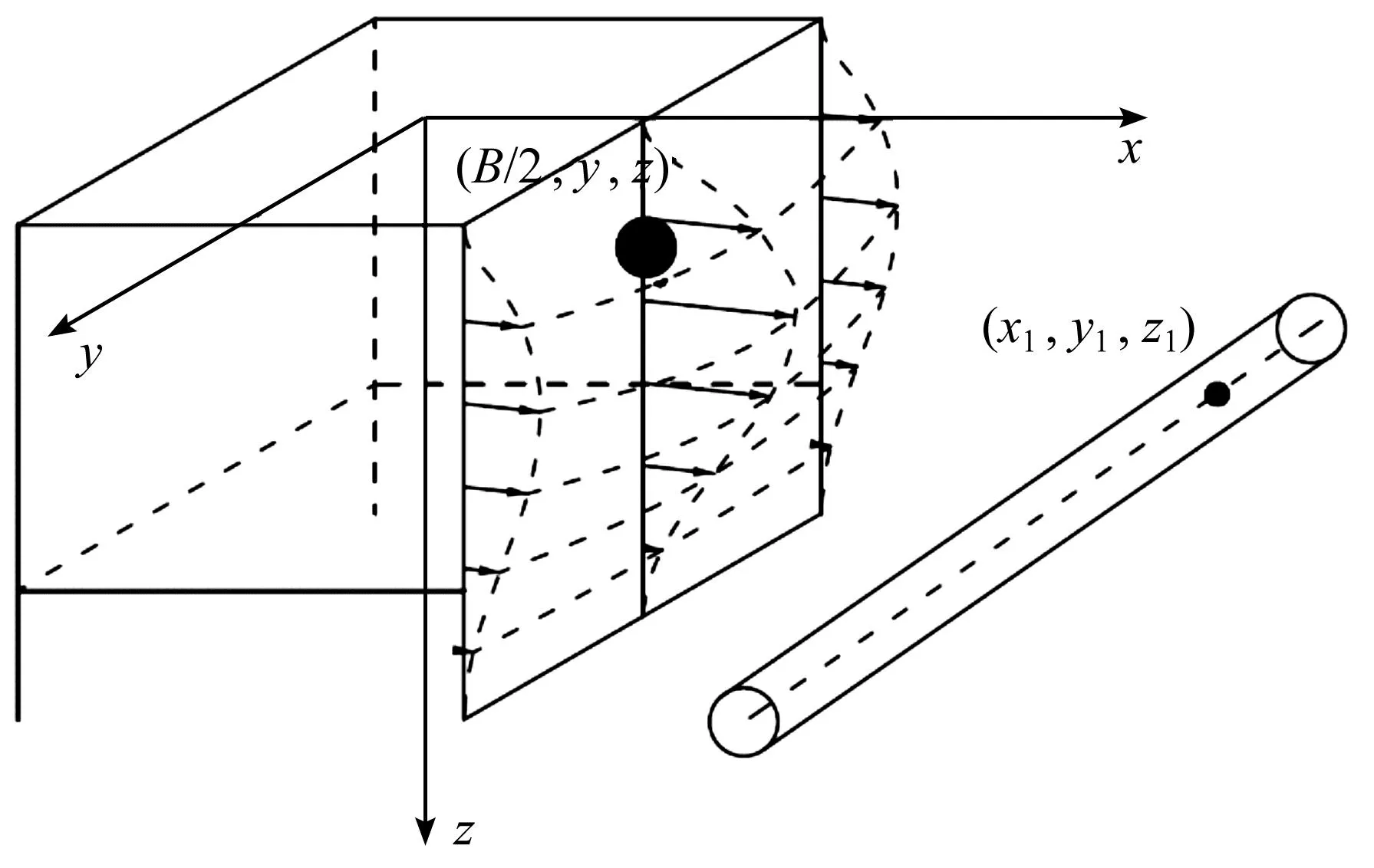
图3 影像源法计算模型Fig.3 Virtual image technique calculation model
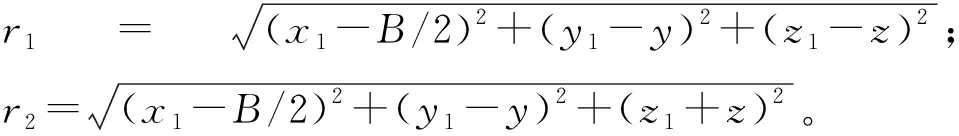
侧壁上点(B/2,y,z)处发生大小为v0的水平位移,根据等效体积原则把侧壁微分后得到
(7)
将式(7)代入式(6),得到点(B/2,y,z)产生的大小为v0的水平位移引起的点(x1,y1,z1)处土体竖向位移为
(8)
对整个侧壁进行积分,得到整个侧壁变形在点(x1,y1,z1)处产生的土体竖向位移为
(9)
同理,邻近管线侧壁上一点(B/2,y,z)半径为a的间隙在管线轴线上的点(x1,y1,z1)处产生的位移沿x轴分量为
(10)
则整个侧壁变形在点(x1,y1,z1)处产生的水平位移为
(11)
1.6 附加荷载计算
以竖向变形计算为例,整个侧壁引起点(x1,y1,z1)点处竖向附加荷载为
Fz(y1)=k·S′z·D
(12)
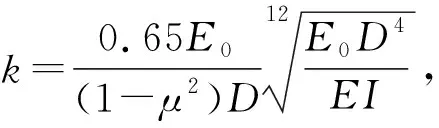
1.7 弹性地基梁求解
基于Pasternak弹性地基梁模型(图4),将管线模拟为搁置在一系列弹簧上的无限长梁,且弹簧上有一土体剪切层以考虑土体连续性。在附加荷载的作用下,管线以及土弹簧发生变形。
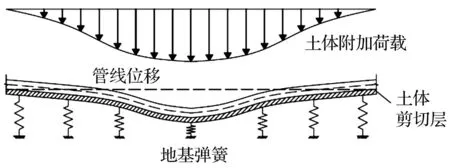
图4 Pasternak地基计算模型Fig.4 Pasternak model
管线与地层相互作用的力学方程式为
(13)
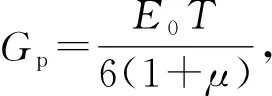
采用有限差分对式(13)进行求解,管线离散如图5所示,在管线两端各增加2个虚节点,每个单元长度为l,将式(13)写成差分形式,即
(14)
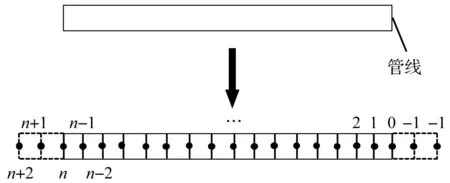
图5 管线离散分析Fig.5 Discrete analysis of pile
管线两端自由条件为
(15)
(16)
(17)
(18)
消除虚节点位移后式(14)可改写为矩阵形式,即
KtS+KsS-GS=F
(19)
式中:Kt为管线位移刚度矩阵;Ks为地基刚度矩阵;S为桩基水平位移列向量;F为附加荷载列向量。具体为
(20)
S=[S0S1S2…Sn]T
(21)
(22)
(23)
F=[F0F1F2…Fn]T
(24)
在附加荷载已知的情况下,结合式(14~24)便可求得基坑开挖引起的地下管线位移。
1.8 考虑管线老化及部分破损
地下管线刚埋设时,管线各点刚度可以认为相同,均为管线初始刚度,即
EiIi=EI
(25)
管线随着使用年限的增加,不可避免地会出现老化及破损情况。魏纲等[25]定义了与时间t相关的管线强度折减系数α=1-t/100,以此来考虑管线老化因素。于是管线在使用t时间之后,管线各点刚度为
EiIi=αEI
(26)
将式(26)代入1.7节计算步骤中,即可得到考虑管线老化的基坑开挖引起邻近地下管线位移解。
当管线出现部分破损,破损位置的管线刚度同样会减小,定义破坏后与破坏前的同一位置管线刚度比为β,假设管线节点p~q之间管线发生了破损,此时管线上各点刚度为
(27)
将式(27)带入1.7节计算步骤中,即可得到考虑管线部分破损的基坑开挖引起的邻近地下管线位移解。
2 实例验证及分析
选取4个邻近基坑的地下管线工程案例,采用笔者方法计算管线的沉降和水平位移,计算沉降值与文献[6]法计算值以及实测沉降曲线进行对比,以验证笔者方法的正确性。选取文献中均未提及的管线使用状态及年限,因此以下案例不考虑管线老化和破损因素。
2.1 工程实例1
JN站基坑尺寸为240.0 m×21.3 m,挖深19.5 m[26],支护结构采用内支撑体系。沿基坑长度方向平行设置编号为P3的DN1200排水管,外径为1 246 mm,壁厚为23 mm,材质为混凝土,埋深为6.71 m,与基坑净距为4.89 m,E=2.85×104MPa。土体弹性模量为80 MPa,μ=0.26。算例中vmax/d=0.075%。
管线沉降计算值与实测值的对比如图6所示。笔者方法计算值与实测值较吻合,验证了笔者方法的可靠性。文献[6]法计算值低估了管线隆起范围,原因是其在预测地表沉降曲线时,仅考虑基坑长度范围内土体沉降。实测数据显示基坑开挖引起的管线最大沉降值出现在开挖区间内,最大值为6.9 mm。基坑开挖中心附近的管线沉降值较大,向两侧递减。管线沉降的影响范围为两侧各150 m左右。笔者方法计算得到的管线水平位移曲线(水平位移值为负号表示变形朝向基坑侧)如图7所示,水平位移最大为-6.3 mm,影响范围与沉降曲线相近。
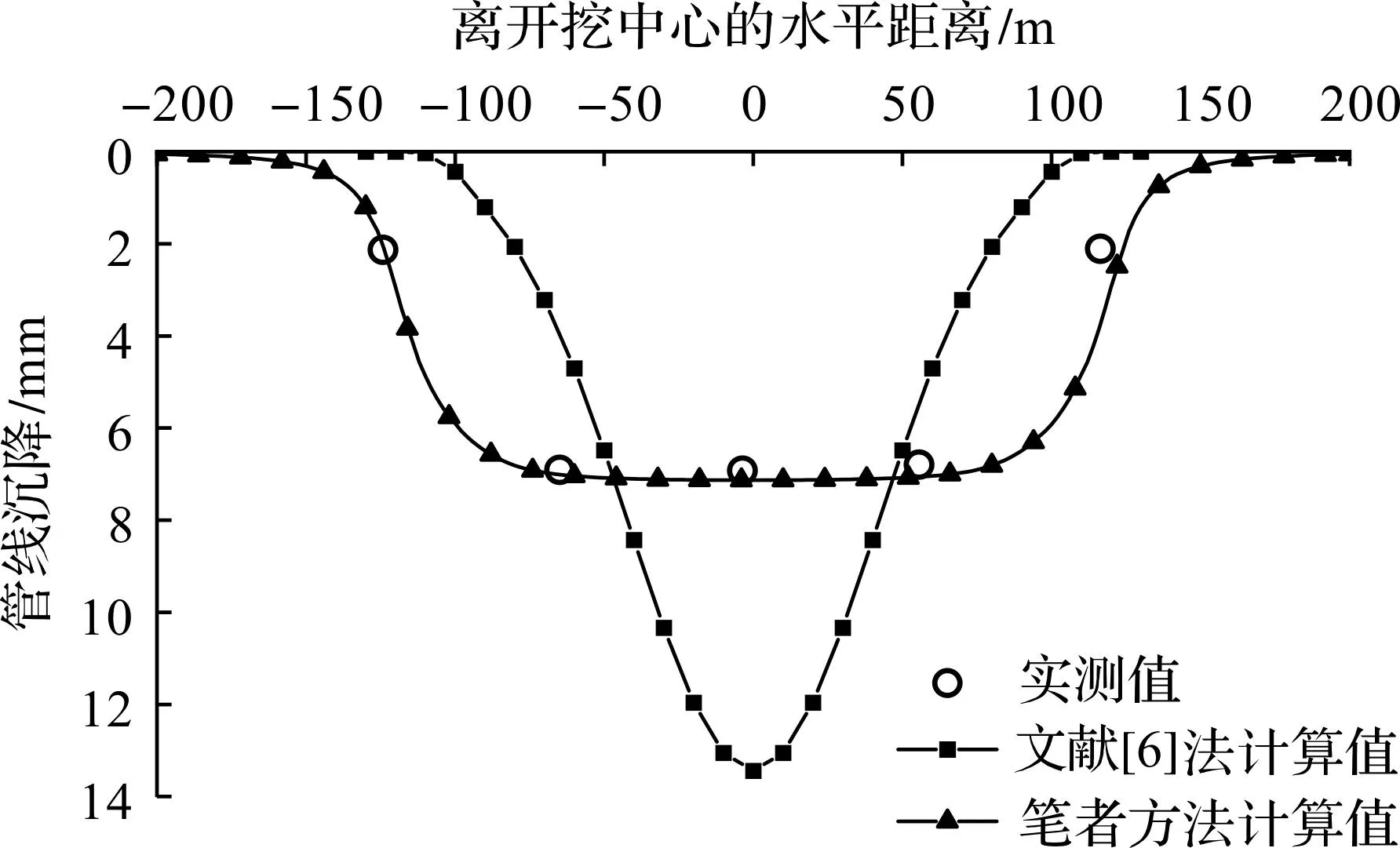
图6 工程实例1管线沉降变形计算对比Fig.6 Calculation and comparison of settlement deformation of the pipeline in engineering case 1
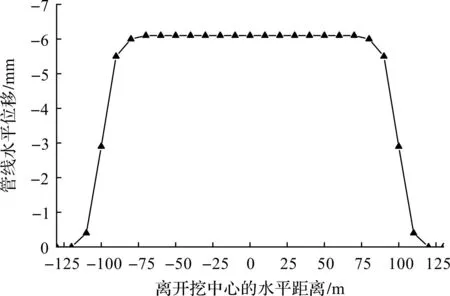
图7 工程实例1管线水平位移计算Fig.7 Calculation of horizontal displacement of the pipeline in engineering case 1
2.2 工程实例2
浦东新区某基坑尺寸为101.5 m×56.4 m,切去东北角35.3 m×21.4 m,挖深为22.0 m,有一埋深1 m的钢材管道,管厚为4 mm,管径为300 mm,距基坑边约为5.87 m[7]。土体压缩模量为6.1 MPa,μ=0.33。算例中vmax/d=0.28%。
笔者方法沉降计算值、文献[6]法计算值与实测值的对比如图8所示。笔者方法计算值与实测值较为吻合。与实例1相比,由于实例2基坑开挖范围较小,管线沉降范围相应较小。文献[6]法同样低估了管线沉降影响范围。实测数据显示:管线最大沉降值为37.3 mm,沉降规律与实例1相似。
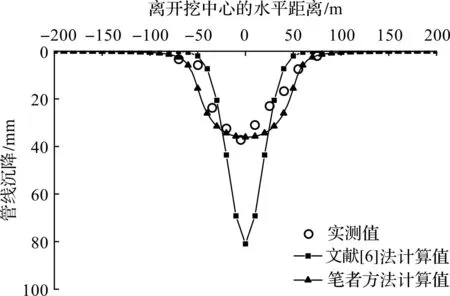
图8 工程实例2管线沉降变形计算对比Fig.8 Calculation and comparison of settlement deformation of the pipeline in engineering case 2
2.3 工程实例3
西安某竖井基坑尺寸为28 m×18 m,挖深为26 m,有一DN600给水管线,管道外径为630 mm,壁厚为60 mm,管线埋深为2 m,距离基坑边缘为5 m[27]。土体弹性模量为80 MPa,μ=0.3。算例中vmax/d=0.045%。
笔者方法沉降计算值、文献[6]法计算值与实测值的对比如图9所示。笔者方法计算值与实测值较吻合。相较于实例1,2,实例3开挖范围最小,因此沉降范围最小。
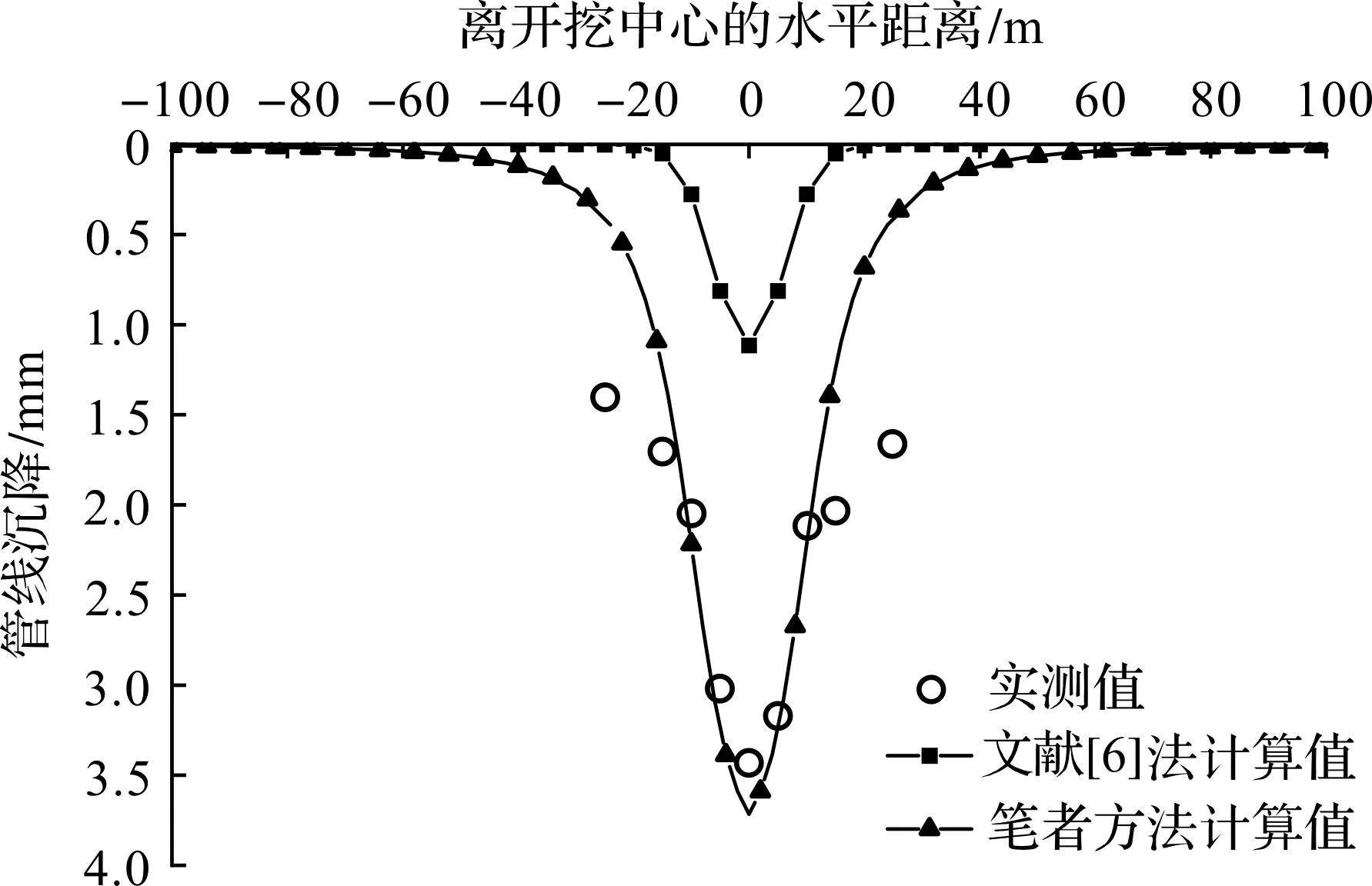
图9 工程实例3管线沉降变形计算对比Fig.9 Calculation and comparison of settlement deformation of the pipeline in engineering case 3
2.4 工程实例4
上海某地下变电站工程基坑尺寸为166 m×68.4 m,挖深为25.3 m[8],距基坑边约为10.5 m有一钢质煤气管线,埋深为1.3 m,管径为500 mm,壁厚为4 mm,弹性模量为200 GPa,μ=0.3。土体弹性模量为200 MPa,μ=0.33。算例中vmax/d=0.28%。
笔者方法沉降计算值、文献[6]法计算值与实测值的对比如图10所示。笔者方法计算值与实测值较为符合,理论计算值为27.8 mm,实测最大值为28.1 mm。
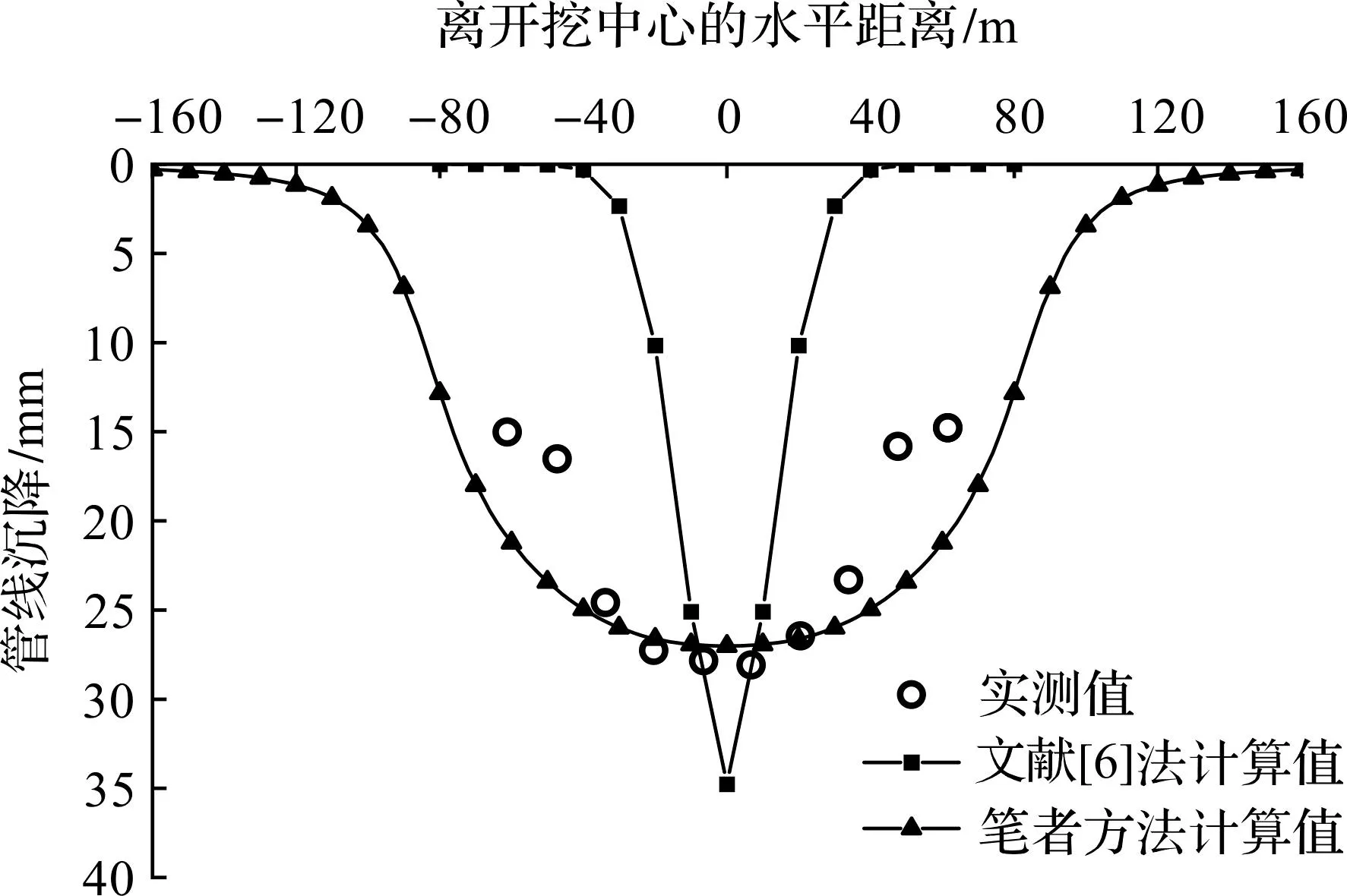
图10 工程实例4管线沉降变形计算对比Fig.10 Calculation and comparison of settlement deformation of the pipeline in engineering case 4
3 影响因素分析
以工程实例2工况为例,分析基坑围护结构变形控制参数vmax/d、管线轴线埋深h、管线轴线到基坑围护结构的水平距离s、管线使用年限以及破损因素对管线沉降的影响。
3.1 围护结构变形控制参数vmax/d的影响因素分析
实测数据统计显示基坑开挖深度与基坑围护结构累计最大变形密切相关[28-30]。杭州地区的基坑围护结构的vmax/d为0.09%~0.32%[28],平均值为0.26%。徐中华等[29]统计的上海地区基坑变形vmax/d为0.1%~1.0%,平均值为0.42%。苏州地区地连墙围护结构vmax/d则为0.05%~0.40%[30]。
只改变基坑围护结构变形控制参数vmax/d,分别令vmax/d为0.05%,0.25%,0.45%,0.65%,0.85%,其他参数不变,计算结果如图11所示。
由图11可知vmax/d改变对管线沉降变形的影响较大。基坑围护结构变形随着vmax/d的增加而增大,导致基坑周边土体变形增加,进而对管线的影响增强,管线最大沉降值相应增加。另外,随着vmax/d增加,管线沉降范围有所增加,vmax/d从0.05%增加到0.85%,管线纵向最大沉降值从6.45 mm增加至109.65 mm,两者呈正相关关系。
3.2 管线轴线埋深h的影响因素分析
只改变管线轴线埋深h,令h分别为2,4,6,8,10 m,其他参数不变,计算结果如图12所示。由图12可知:随着管线轴线埋深h的增加,管线沉降量随之减小,然而沉降影响范围几乎不变。管线轴线深度h从10 m减小到2 m,5种不同工况下管线最大沉降分别增加了41.9%,27.1%,16.8%,8.9%。管线受基坑开挖影响随着管线埋深的减小而变大,管线最大沉降值也随之增加,然而增加的幅度逐渐减小。刘小兵等[7]同样得到管线竖向位移与其埋深呈非线性减小的结论。
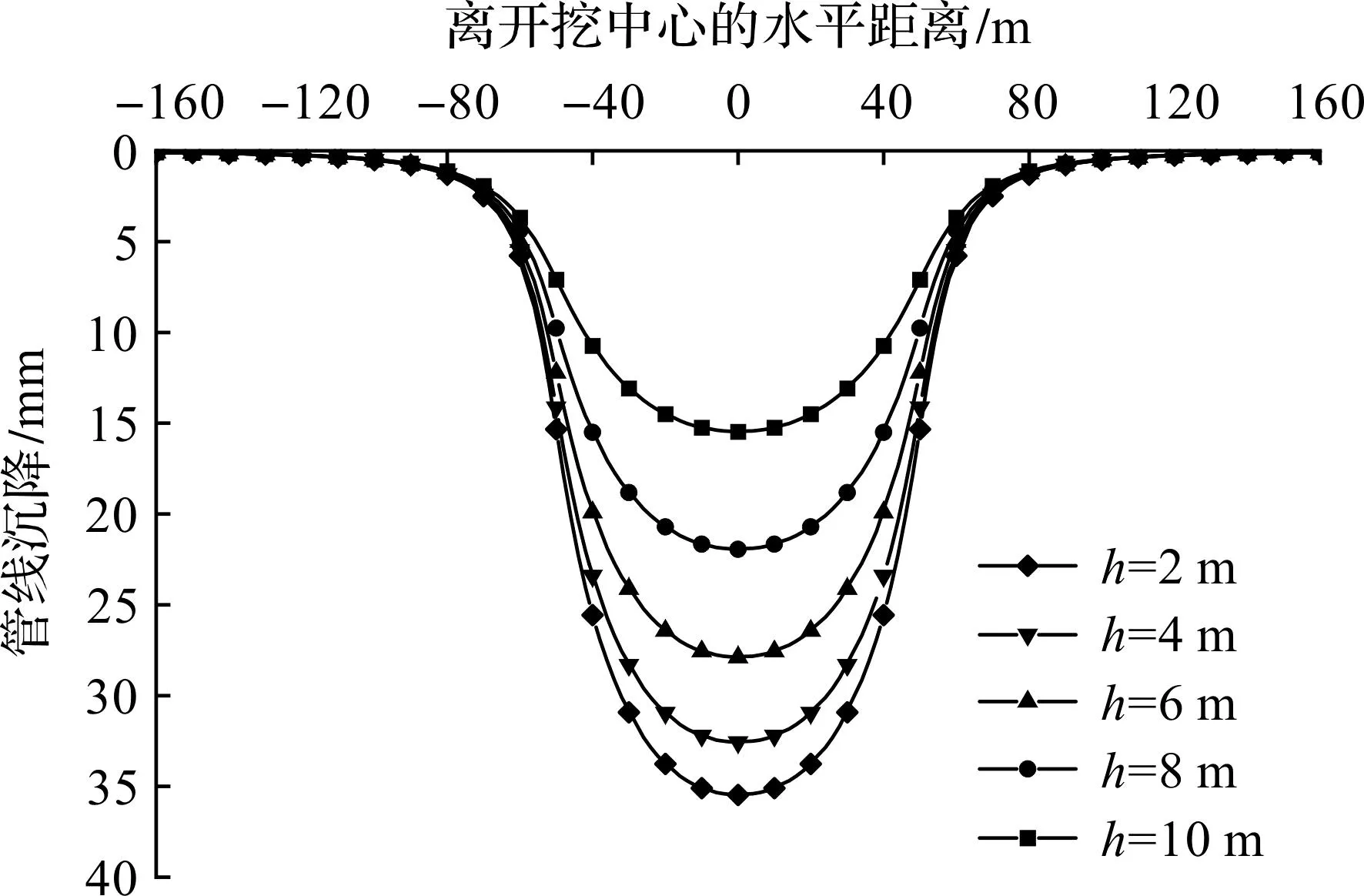
图12 不同h时管线沉降变形Fig.12 Settlement deformation of the pipeline with different values of h
3.3 管线轴线到基坑围护结构的水平距离s的影响因素分析
只改变管线轴线到基坑围护结构的水平距离s,令s分别为5,10,15,20,25 m,其他参数不变,计算结果如图13所示。由图13可知:随着管线轴线到基坑围护结构水平距离s的减小,不仅管线沉降量随之增加,而且沉降影响范围也有所增加;随着管线轴线到基坑围护结构水平距离s的增加,受基坑围护变形的影响逐渐减小,管线最大沉降值随之减小,且减小的幅度逐渐变小。李大勇等[9]同样得到管线距离基坑越近,其位移越大的结论。
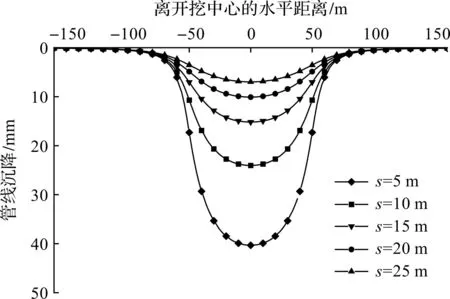
图13 不同s时管线沉降变形Fig.13 Settlement deformation of the pipeline with different values of s
3.4 管线使用年限t的影响因素分析
假设管线使用年限分别为0,20,40,60,80 a,其他参数不变,计算结果如图14所示。由图14可知:随着管线使用年限t的增加,管线刚度逐渐减小,管线抵抗变形能力同样随着刚度的减小而减小,管线变形逐渐增大。当管线使用年限为0时,管线最大沉降为36.12 mm,而当管线使用年限达到80 a后,管线最大沉降达到41.3 mm。因此在基坑开挖过程中对邻近地下管线的年限调查同样是必要的。
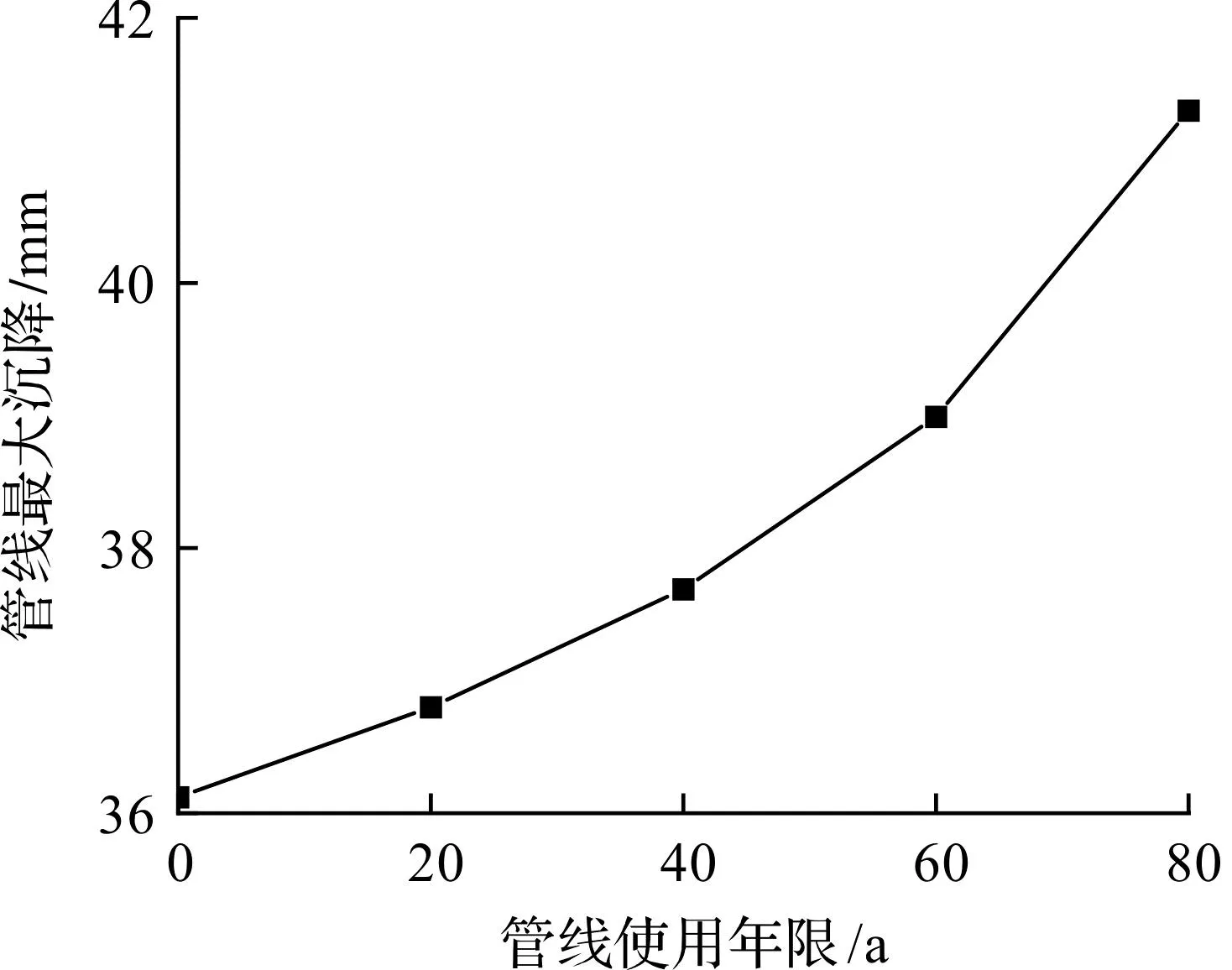
图14 不同t时管线沉降变形Fig.14 Maximum settlement deformation of the pipeline with different values of t
3.5 管线破损的影响因素分析
假设管线在距开挖中心10~15 m位置处发生破损,破损位置管线刚度为βEI,取一半分析,管线沉降曲线如图15所示。由图15可知:管线会在破损位置产生额外沉降量,极大地影响了管线的正常使用,而管线破损程度越高,破损位置的额外沉降也越大。
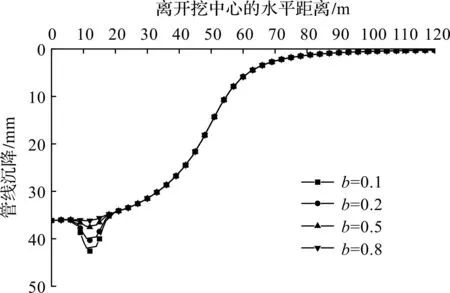
图15 不同管线破损程度时管线沉降变形Fig.15 Settlement deformation of the pipeline at different degree of pipeline breakage
4 结 论
将影像源法应用于基坑围护结构变形对邻近地下管线变形影响的计算研究中,该方法参数较少,计算更为简便。基于笔者研究,得出如下结论:1) 笔者方法管线竖向位移计算结果与实测值较吻合,基坑开挖中心附近处的管线竖向以及水平位移较大,沿着管线轴线逐渐减少,呈正态分布规律;2) 管线沉降量与围护结构变形呈正相关关系,随着基坑围护结构变形增大,对管线纵向变形影响及影响范围也随之增大;3) 管线沉降随着管线埋深以及基坑侧壁与管线轴线距离的增加呈非线性减小的规律;4) 笔者在分析过程中稍作了简化,如忽略降水、管线和土体的非线性作用,忽略地基土的分层、地面荷载和土体收敛等非均匀性等影响,理论结果会有一定误差,未来可在本研究基础上作进一步探索。
