不同曲线半径下轨底坡与轮径差最佳匹配研究

朱爱华,孟宇轩,张 帆,杨建伟,郭宇轩

(北京建筑大学 城市轨道交通车辆服役性能保障北京市重点实验室,北京 100044)

轨底坡是轨道的重要参数,轨底坡存在误差或设置不合理会影响车辆动力学性能,也会对车辆和钢轨造成不同程度的损伤。轮径差属于车轮损伤的一种类型,不仅影响车辆的动力学性能,还会使车轮踏面磨耗现象加剧,严重缩短车轮服役期限。针对轨底坡的研究:任德祥等[1-2]首先分析了地铁非对称轨底坡对不同车轮型面下轮轨接触几何特性和接触力学特性的影响,得到不同型面下轨底坡的推荐数值,然后进一步对地铁车轮异常磨耗现象进行研究,发现轨底坡较大会导致轮轨型面匹配不合理,进而导致车辆轮缘和踏面异常磨耗,最后提出了将车轮踏面外形由S1002镟修为LM以改善车轮异常磨耗的建议;陶功权等[3-4]分析了3种类型的地铁车轮踏面和CHN60钢轨匹配时,轨底坡对轮轨接触几何、轮轨接触力学、车辆稳定性、曲线通过性能以及车轮磨耗的影响,分别从静力学和动力学的角度提出地铁车轮型面的最优轨底坡匹配;赵越等[5]在进行机车JM3型和货车LM型踏面与CHN75钢轨匹配时,分析了轨底坡对轮轨匹配状态和轮轨滚动接触的影响;高雅等[6]运用轮轨接触空间迹线法针对轨底坡对轮轨接触几何参数的影响展开分析,同时研究了多工况下轨底坡对车辆服役性能的影响规律;杜星等[7]分析了在标准轨底坡、对称变化轨底坡和非对称变化实测轨底坡条件下的车辆动力学行为,提出了不同线路下轨底坡的工程化建议;温静等[8]针对非对称轨底坡对车辆动力学性能、轮轨磨耗及滚动接触疲劳的影响进行了研究,给出了曲线线路下轨底坡推荐数值。针对轮径差的研究:李洪晓等[9]分析了前后转向架都存在等值同向轮径差对地铁车辆曲线通过性能的影响,发现当列车通过曲线线路时,外侧车轮的动力学响应更剧烈;韩鹏等[10]通过研究滚动半径差函数形状与位置的变化规律,分析得到型面磨耗和轮径差对高速列车动力学性能的影响规律;李润华等[11]研究了初始轮径差对高速列车动力学性能的影响,并给出了初始轮径差的限度制定标准;蒋益平等[12]分析了各种轮径差组合工况下地铁车辆各种动力学指标的变化规律;严松等[13]针对4种典型轮径差对列车多工况运行性能的影响进行了研究,发现轮径差越大影响越明显;蔡送宝等[14]分析了在车桥耦合情况下,轮径差对车轮磨耗的影响,发现轮径差会导致车轮偏磨,也会改变车轮踏面的磨耗区域;王红兵等[15]发现在4种典型轮径差中,等值同向轮径差导致的车轮踏面偏磨现象最明显。

综上,目前对轨底坡的研究主要集中在不同车轮型面的最优轨底坡匹配及轨底坡对车辆动力学性能及车轮磨耗的影响上。对轮径差的研究主要集中在不同种类的轮径差对车辆动力学及车轮磨耗的影响上。实际上,钢轨与车轮踏面接触面有一定角度,因此通过设置轨底坡来改善轮轨接触,随着服役里程的变化,轨底坡和轮径差都会发生变化,轮径差的改变会导致车轮踏面与钢轨接触角度的改变,从而加剧轮轨接触状态的变化,影响车辆的动力学性能。因此,考虑不同轨底坡和轮径差耦合工况下车辆动力学指标变化规律,进而研究轨底坡与轮径差最优匹配方案具有重要意义。笔者建立了地铁车辆动力学模型,对9种不同轨底坡工况和5种等值同向轮径差工况在4种曲线半径条件下的轮轨横向力、轮对横移量、脱轨系数、轮重减载率和磨耗指数进行分析,并通过熵权法对各指标加权求和,得到不同半径曲线下轨底坡和轮径差耦合工况车辆动力学性能的综合得分,获得4种曲线半径下轨底坡和轮径差的最优匹配方案。

1 地铁车辆动力学模型

1.1 动力学模型

运用SIMACK软件建立如图1所示的国内某地铁车辆动力学模型。该模型包括1个车体、2个构架、4个轮对、8个轴箱和一系、二系悬挂系统。车轮型面选取LM型踏面,钢轨选取UIC60轨,轨距为1 435 mm,摩擦系数为0.4。列车参数设置如表1所示。

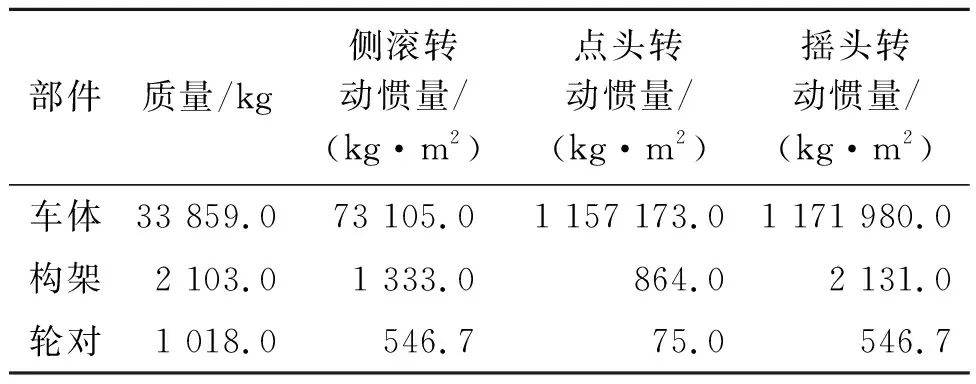
表1 列车主要参数

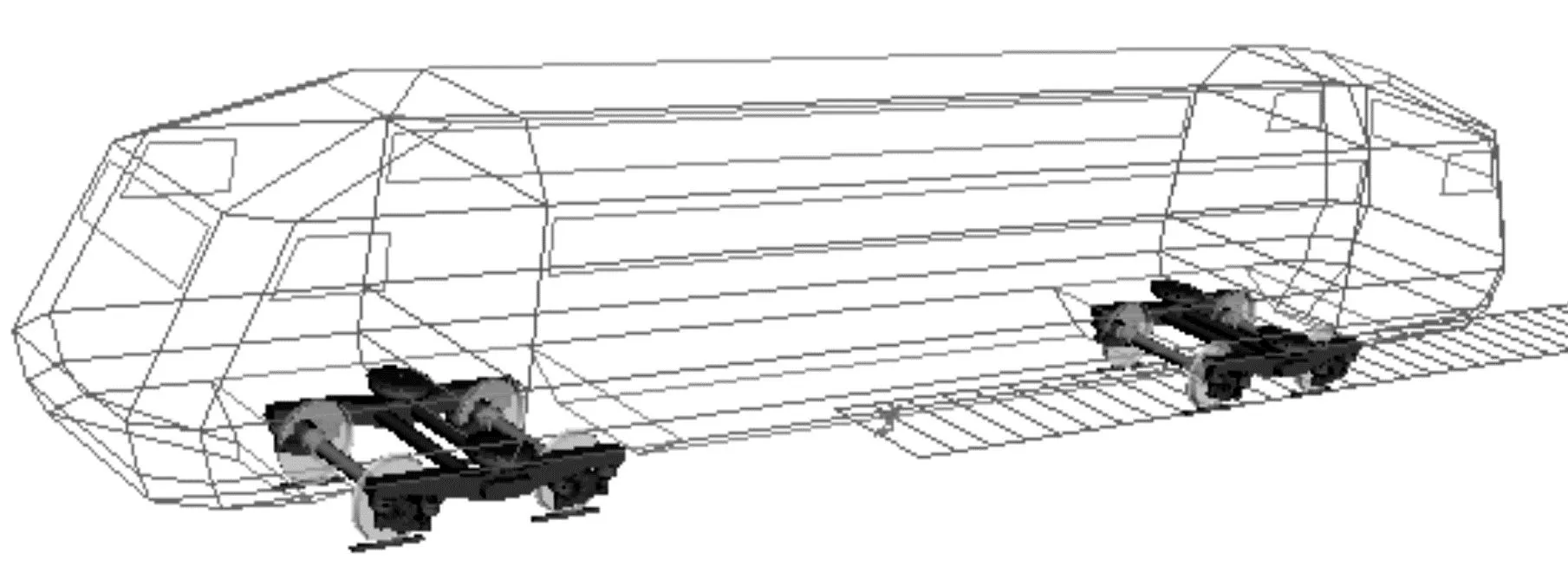
图1 车辆动力学模型Fig.1 Vehicle dynamics model

1.2 轨底坡工况设置

因为轮轨间的接触面有一定的角度,所以需要设置轨底坡来提高轮轨接触的稳定性,根据《地铁设计规范》(GB 50157—2013),目前我国铁路普遍使用1/40轨底坡,也有部分地铁线路采用1/20轨底坡,经过磨耗后轨底坡的数值一般为1/40～1/20。因此,在1/40～1/20之间设置了9种不同的轨底坡工况。轨底坡工况如表2所示。

表2 轨底坡工况

1.3 轮径差设置

在SIMPACK软件中通过Wheel geometry模块建立轮径差模型,轮径差为两侧车轮名义滚动圆处直径的差值,轮对轮径差定义为

ΔD=D内-D外

(1)

式中:D内为内侧车轮的直径;D外为外侧车轮的直径;ΔD>0表示外轨轮径小于内轨轮径。

在实际运行过程中,由于不同轮对磨耗程度不尽相同,故会产生各种类型的轮径差,由于线路的影响,等值同向轮径差比较常见,而且与其他类型相比,等值同向轮径差对列车动力学性能和车轮磨耗的影响最为明显[13-15],为了使每一侧车轮工况保持一致,前后转向架都设置了等值同向轮径差,等值同向轮径差工况如图2所示。

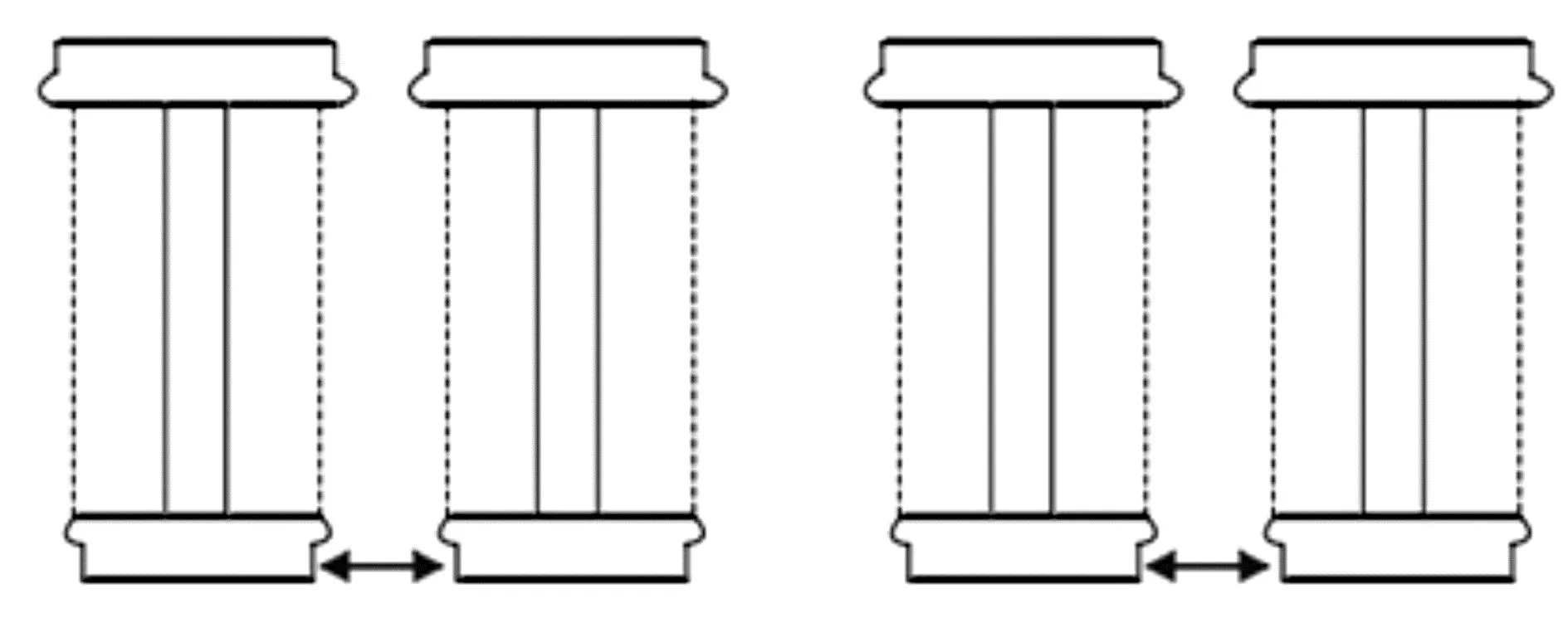
图2 等值同向轮径差工况Fig.2 Condition of wheel diameter difference of equal value in the same direction

根据《地铁设计规范》(GB 50157—2013)和我国检修规章可知,同轴轮径差超过1 mm时就要进行轮对镟修。轮径差设置如表3所示。

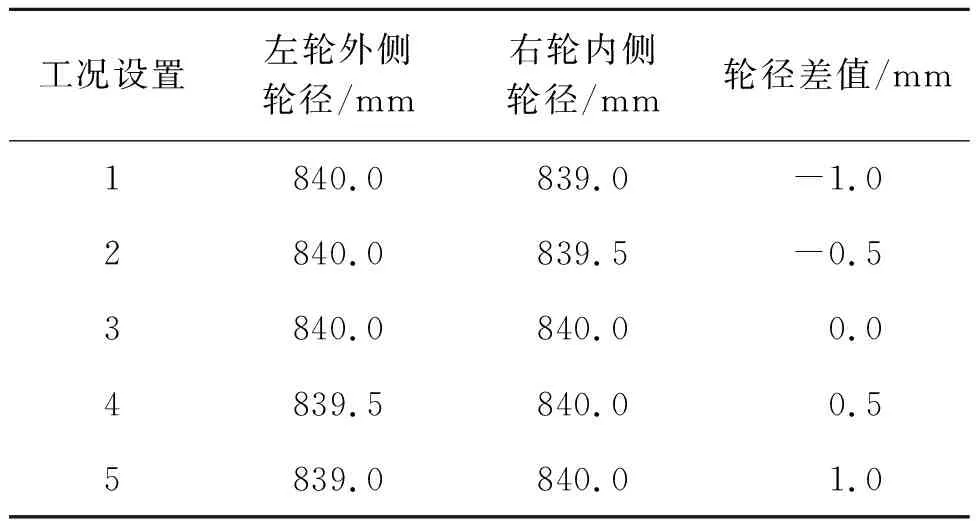
表3 轮径差工况设置

1.4 线路工况设置

因为地铁车辆主要在城市建筑群周边运行,所以运营线路中小半径曲线较多,而且小半径曲线线路极易导致车轮损伤。根据《地铁设计规范》(GB 50157—2013),笔者选取4种不同半径曲线作为研究对象,线路总长为1 000 m,曲线为右转C型曲线,速度为60 km/h匀速,轨道不平顺选取德国高干扰谱,线路主要参数如表4所示。

表4 线路主要参数

2 基于熵权法的综合评价

选取轮轨横向力、脱轨系数、轮重减载率、轮对横移量以及外轨侧车轮磨耗指数有效值和内轨侧车轮磨耗指数有效值作为地铁车辆动力学性能的评价指标。该6项指标单位不同,量纲也不同,数据的性质更是不尽相同,因此笔者采用熵权法,将多指标问题按照一定规则转换为单指标问题,再通过线性加权的方法得到一个综合得分,用来综合评判地铁车辆的动力学性能。

2.1 熵权法的原理

熵权法是一种依赖于数据本身变化规律的客观赋权法,其指标权重的大小根据数据本身变化特性进行权重赋予,若某一指标的信息熵越小,则说明该指标的样本变化越剧烈,提供的信息量越大,其权重系数也就越大[16]。

2.2 熵权法的步骤

选取的轮轨横向力、脱轨系数、轮重减载率、轮对横移量以及轨道两侧车轮磨耗指数有效值这6个评价指标的量纲、单位不同,其数值均是越小越好。先对仿真得到的数据进行负向指标0～1归一化处理,将各项评价指标统一到[0,1]区间,其计算式为

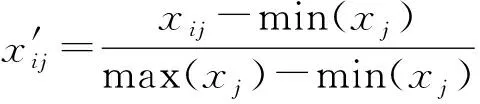
(2)

式中:x′ij为归一化的数据;xij为第i个数据组的第j个指标;max(xj)为第j个指标中的最大值;min(xj)为第j个指标中的最小值。

计算第j项指标下第i个样本值占该指标的比重,即

(3)

式中:pij为第j项指标下第i个样本值占该指标的比重。

计算第j项指标的熵值和信息熵冗余度,即

(4)

dj=1-ej

(5)

式中:ej为第j项指标的熵值,且k=1/lnn>0,并满足ej≥0;dj为熵值冗余度。

计算各样本的权重,得到不同半径曲线下这6个指标的权重系数wj,即

(6)

通过对不同工况下的6个指标进行加权求和得到不同工况下各样本的综合得分si,即

(7)

3 计算结果分析

建立地铁车辆动力学仿真模型,设置了45种轨底坡和轮径差耦合工况,分析在4种不同C型曲线半径条件下,轮轨横向力、脱轨系数、轮重减载率、轮对横移量和轮轨磨耗指数的变化规律。

3.1 轮轨横向力

轮轨横向力是地铁列车曲线通过性能的重要评价指标,轮轨横向力Q计算式为

Q≤0.4(Pst1+Pst2)

(8)

式中:Pst1,Pst2分别为左轮及右轮静载荷,kN。

不同曲线半径下轮轨横向力峰值如图3所示。由图3可知:1) 在4种曲线半径条件下,当轨底坡恒定时,随着轮径差从-1 mm变化至1 mm,轮轨横向力峰值均逐渐变大;2) 在曲线半径为300,400 m条件下,当轮径差恒定时,轨底坡对轮轨横向力峰值的影响并不是很明显,在曲线半径为500,600 m条件下,当轮径差恒定,内轨轨底坡不变时,随着外轨轨底坡的增大,轮轨横向力峰值逐渐变大,与内轨轨底坡相比,外轨轨底坡的变化对轮轨横向力峰值的影响更大;3) 随着曲线半径的增大,轨底坡和轮径差对轮轨横向力峰值的影响程度在逐渐变大。

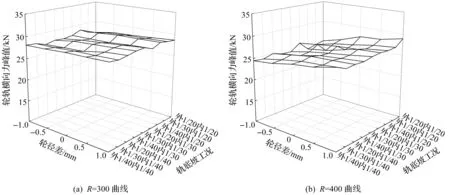
图3 不同曲线半径下轮轨横向力峰值Fig.3 Peak wheel-rail lateral force under different curve radii

3.2 轮对横移量

轮对横移量是评价列车曲线通过性能的重要指标,轮对横移量较大时会发生轮缘接触,从而导致踏面异常磨耗,恶化轮轨接触关系。不同曲线半径下列车轮对横移量峰值如图4所示。由图4可知:1) 在4种曲线半径条件下,当轨底坡恒定时,随着轮径差从-1 mm变化至1 mm,轮对横移量峰值均逐渐变大;2) 在4种曲线半径条件下,当轮径差恒定,内轨轨底坡不变时,随着外轨轨底坡的增大,轮对横移量峰值逐渐变大;3) 随着曲线半径的增大,轨底坡和轮径差对轮对横移量峰值的影响程度逐渐变大,当轨底坡和轮径差恒定时,随着曲线半径的增大,轮对横移量逐渐减小。

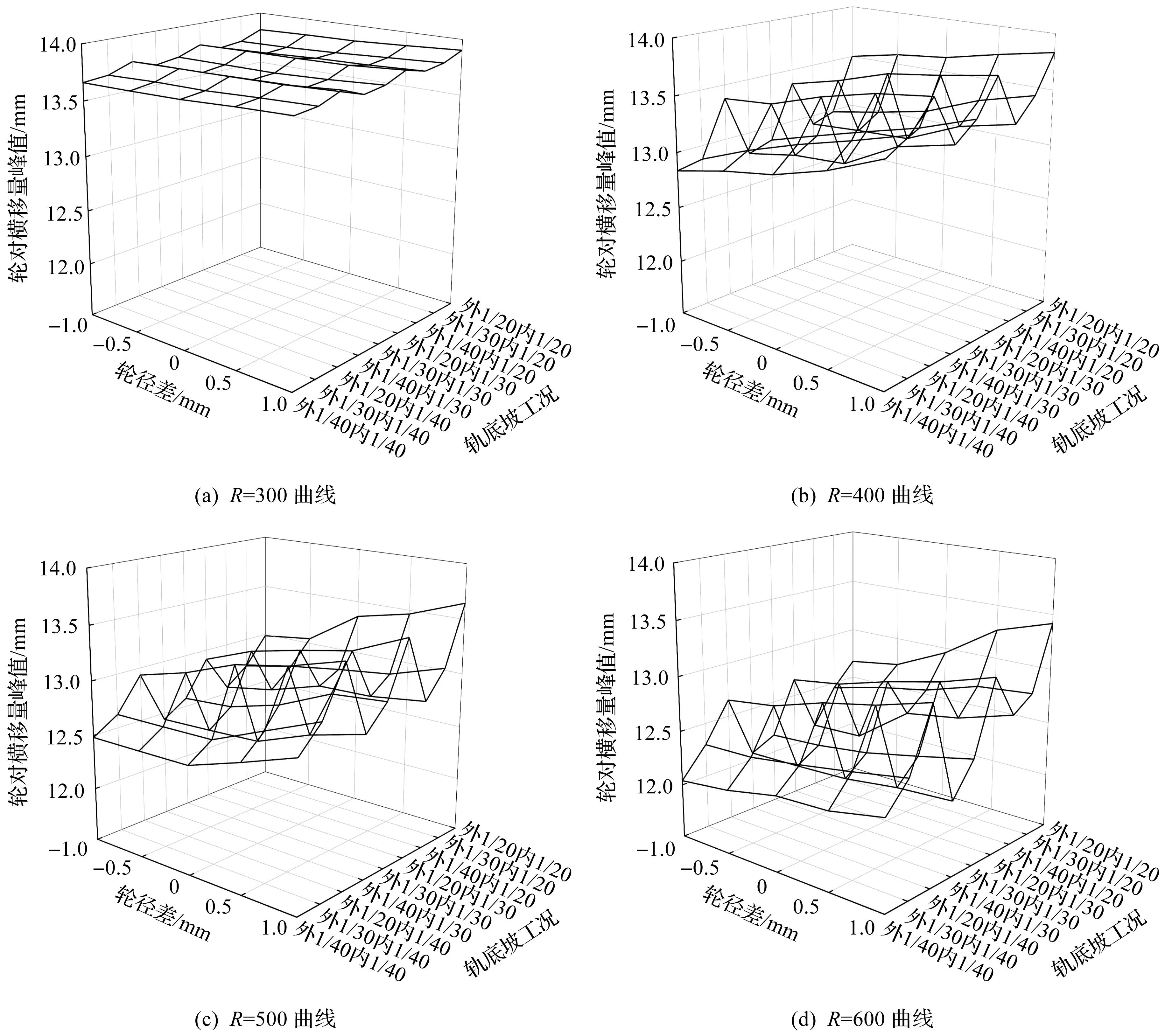
图4 不同曲线半径下列车轮对横移量峰值Fig.4 Peak values of wheelset traverse under different curve radii

3.3 脱轨系数

车辆运行过程中,运行环境和线路条件等不利因素均可导致列车发生轮轨分离现象,继而威胁车辆运行质量以及乘客生命安全。根据《机车车辆动力学性能评定及试验鉴定规范》(GB 5599—2019),脱轨系数安全值为0.8,即

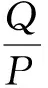
(9)

式中:P为轮轨垂向力,kN;Q为轮轨横向力,kN。

不同曲线半径下脱轨系数峰值如图5所示。由图5可知:1) 在4种曲线半径条件下,当轨底坡恒定时,随着轮径差从-1 mm变化至1 mm,脱轨系数峰值均逐渐变大;2) 在曲线半径为300 m条件下,当轮径差恒定时,轨底坡对脱轨系数峰值的影响并不是很明显,在曲线半径为400,500,600 m条件下,当轮径差恒定,内轨轨底坡不变时,随着外轨轨底坡的增大,脱轨系数峰值逐渐变大,当曲线半径大于300 m时,与内轨轨底坡相比,外轨轨底坡的变化对轮轨横向力峰值的影响更大;3) 随着曲线半径的增大,轨底坡和轮径差对脱轨系数峰值的影响程度在逐渐变大。

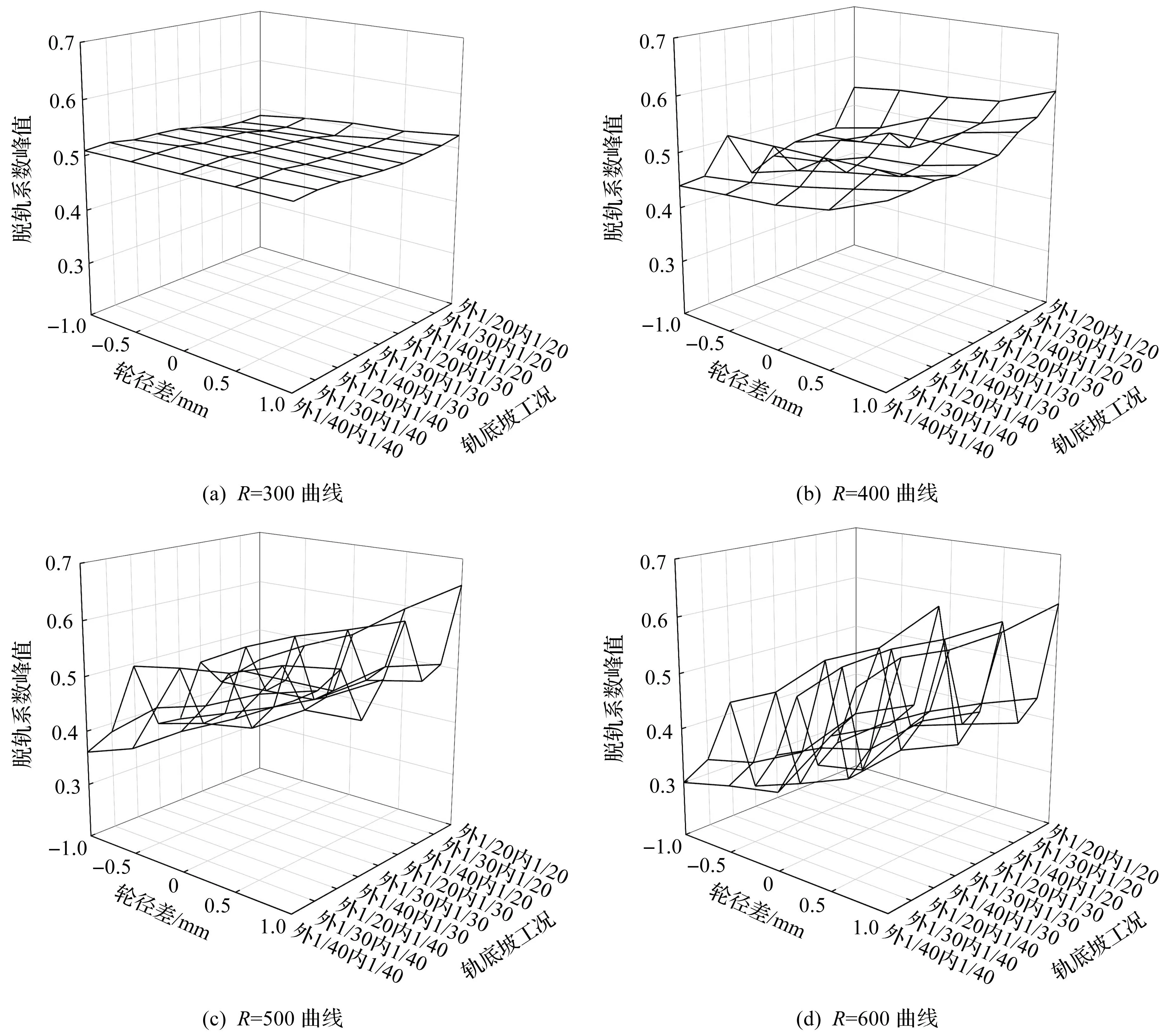
图5 不同曲线半径下脱轨系数峰值Fig.5 Peak value of derailment coefficient under different curve radii

3.4 轮重减载率

不同曲线半径下轮重减载率峰值如图6所示。由图6可知:当轨底坡和轮径差恒定时,随着曲线半径的增大,轮重减载率逐渐变小。相同曲线半径下,轮径差和轨底坡对轮重减载率的影响不是很明显,且变化幅度在0.02以内。当列车速度小于160 km/h时,轮重减载率要控制在0.65以内。所有工况下轮重减载率均在限制范围之内。

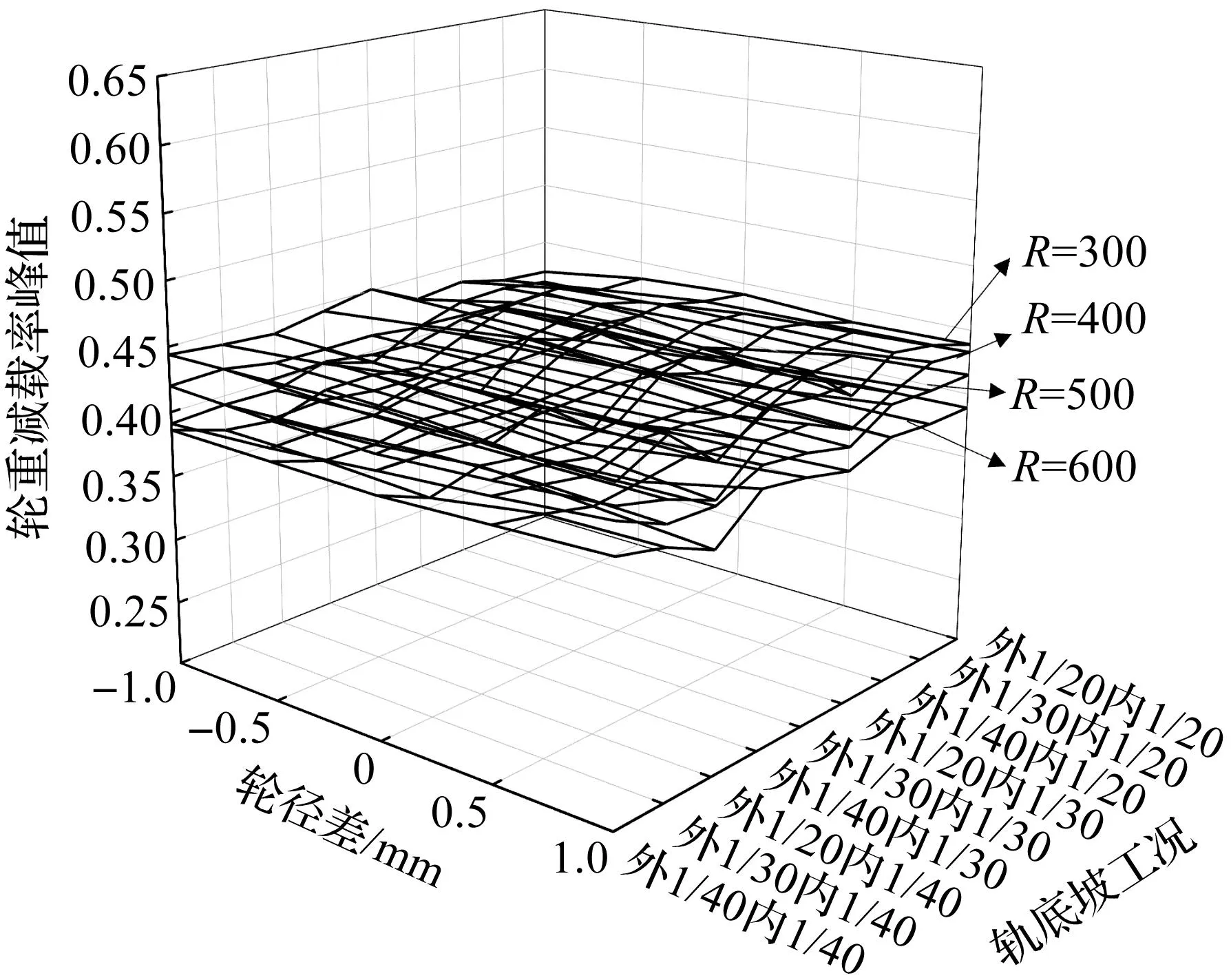
图6 不同曲线半径下轮重减载率峰值Fig.6 The peak value of wheel load shedding rate under different curve radii

3.5 磨耗指数

相较于其他磨耗指数,Elkins磨耗指数更能有效地表示轮轨之间的磨损现象,更适合研究轮轨间的磨耗问题,磨耗指数W的计算式为

W=Txξx+Tyξy

(10)

式中:Tx为横向蠕滑力;ξx为横向蠕滑率;Ty为纵向蠕滑力;ξy为纵向蠕滑率。为了更加准确地反映轮轨的磨耗程度,选取磨耗指数的有效值RMS作为评价指标。

不同曲线半径下车轮磨耗指数有效值如图7所示。由图7可知:1) 在相同轮径差、轨底坡和曲线半径工况下,外轨车轮磨耗指数有效值要大于内轨车轮磨耗指数有效值,而且内外轨车轮的磨耗指数有效值变化规律基本一致;2) 在4种曲线半径条件下,当轨底坡恒定时,随着轮径差从-1 mm变化至1 mm,磨耗指数有效值在逐渐变小,这说明外轨轮径大于内轨轮径工况会加重两侧车轮的磨耗;3) 在4种曲线半径条件下,当轮径差恒定,内轨轨底坡不变时,随着外轨轨底坡的增大,磨耗指数有效值逐渐变小;4) 随着曲线半径的增大,轨底坡和轮径差对磨耗指数有效值的影响程度在逐渐变小;5) 随着曲线半径的增大,内外轨车轮磨耗指数有效值逐渐减小,且内外轨车轮磨耗指数有效值差距逐渐变小,这说明列车通过曲线的半径越小,车轮偏磨越严重;6) 当外轨轨底坡为1/40,内轨轨底坡为1/20,轮径差为-1 mm时,车轮两侧磨耗指数有效值最大,在这个工况下通过半径为300 m曲线,外轨车轮的磨耗指数有效值接近100 N,车轮磨耗已经十分严重,应尽可能避免出现这种工况。

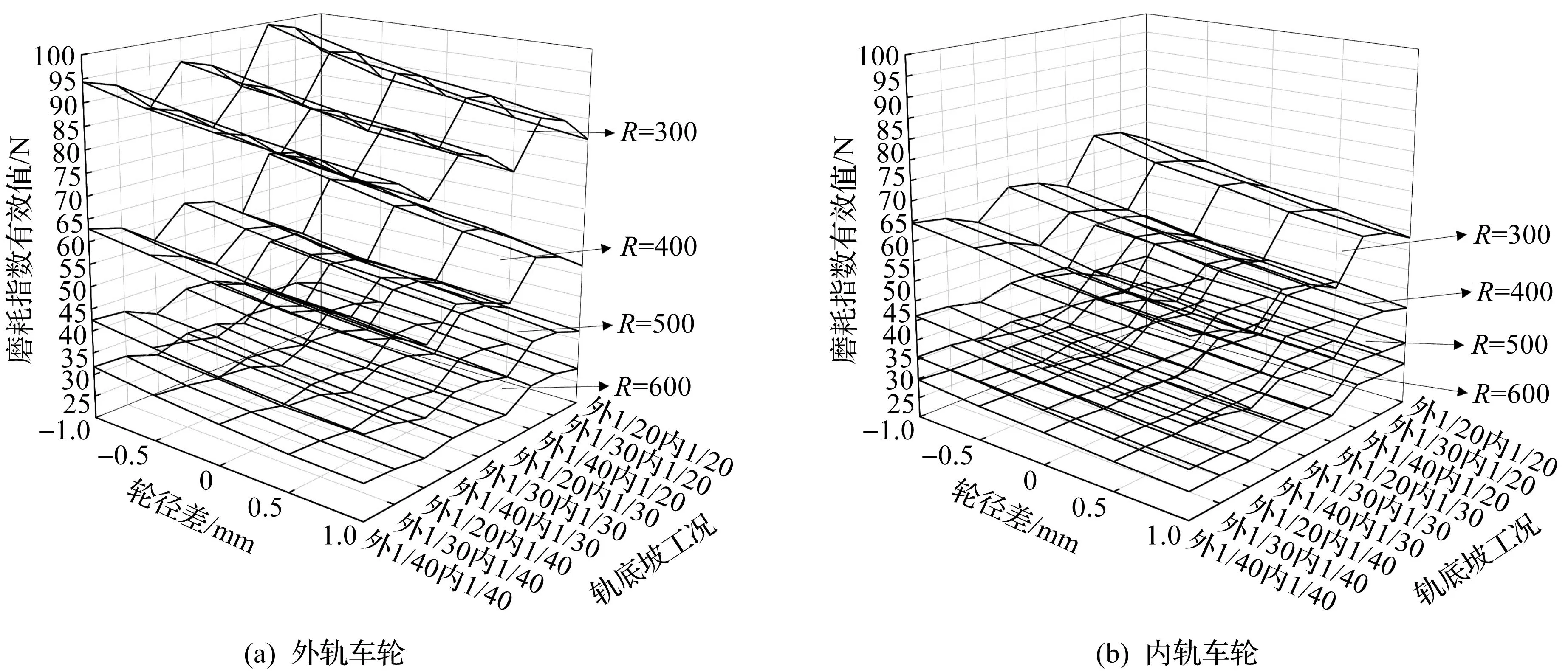
图7 不同曲线半径下车轮磨耗指数有效值Fig.7 Effective value of wheel wear index under different curve radii

4 基于熵权法的车辆动力学性能综合评价

根据轮轨横向力、脱轨系数、轮重减载率、轮对横移量以及内外轨车轮磨耗指数有效值的计算结果,首先进行数据的标准化;然后采用熵权法进行数据分析;最后计算出各项指标在不同曲线半径下的信息熵值和信息熵冗余度,从而求得各项指标的权重,结果如表5所示。

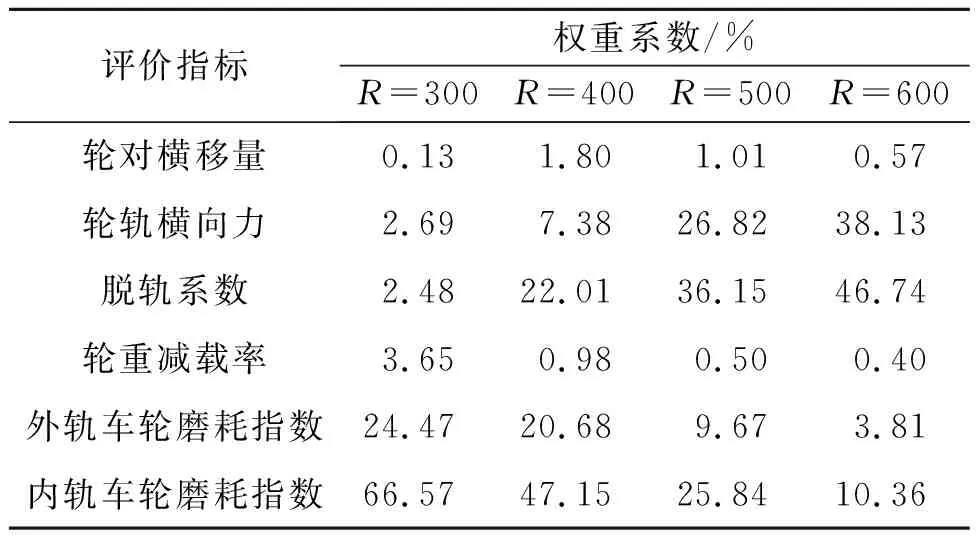
表5 不同曲线半径下各项指标权重系数

由表5可知:在同一个半径曲线下,各项评价指标的权重系数相差十分明显,且曲线半径不同,各项指标规律也不同。在曲线半径为300,400 m时,内外轨车轮磨耗指数的权重系数更大;在曲线半径为500,600 m时,轮轨横向力和脱轨系数所占的权重系数更大。

根据表5的计算结果以及式(7)得到在4种曲线半径条件下不同耦合工况的综合得分。综合得分越低,综合动力学性能越好,对应的列车运行工况越理想,综合得分结果如图8所示。由图8可知:当轮径差和轨底坡工况不变时,随着曲线半径的增大,综合得分逐渐变小,即车辆动力学性能得到改善。当轨底坡工况一定时,轮径差由-1 mm变化至1 mm,曲线半径为300,400 m时对应的综合得分逐渐变小;而曲线半径为500,600 m时对应的综合得分逐渐变大。当轮径差工况一定且内轨轨底坡不变时,随着外轨轨底坡逐渐变大,曲线半径为300,400 m对应的综合得分逐渐变小;而曲线半径500,600 m对应的综合得分逐渐变大。

图8 不同曲线半径下综合得分Fig.8 Comprehensive scores under different curve radii

在同一曲线半径下的45种工况中找出综合得分最低(即车辆动力学性能最佳)的前3种工况,结果如表6所示。由表6可知,以车辆动力学综合性能最优为目标,轨底坡和轮径差最佳匹配规律如下:1) 随着曲线半径的增大,呈现出外轨轨底坡逐渐变小、内轨轨底坡逐渐变大的趋势,当曲线半径为300,400 m时,外轨轨底坡大于内轨轨底坡,当曲线半径为500,600 m时,内轨轨底坡大于外轨轨底坡;2) 随着曲线半径的增大,轮径差数值有变小趋势,从+1 mm变至-1 mm,当曲线半径为300,400 m时,外轨轮径小于内轨轮径,当曲线半径为500,600 m时,外轨轮径大于内轨轮径;3) 在曲线半径为300,400,500,600 m 4种工况下,外轨轨底坡,内轨轨底坡,轮径差最优匹配方案分别为(1/20,1/40,+1),(1/20,1/40,+1),(1/30,1/30,-1),(1/40,1/30,-1)。

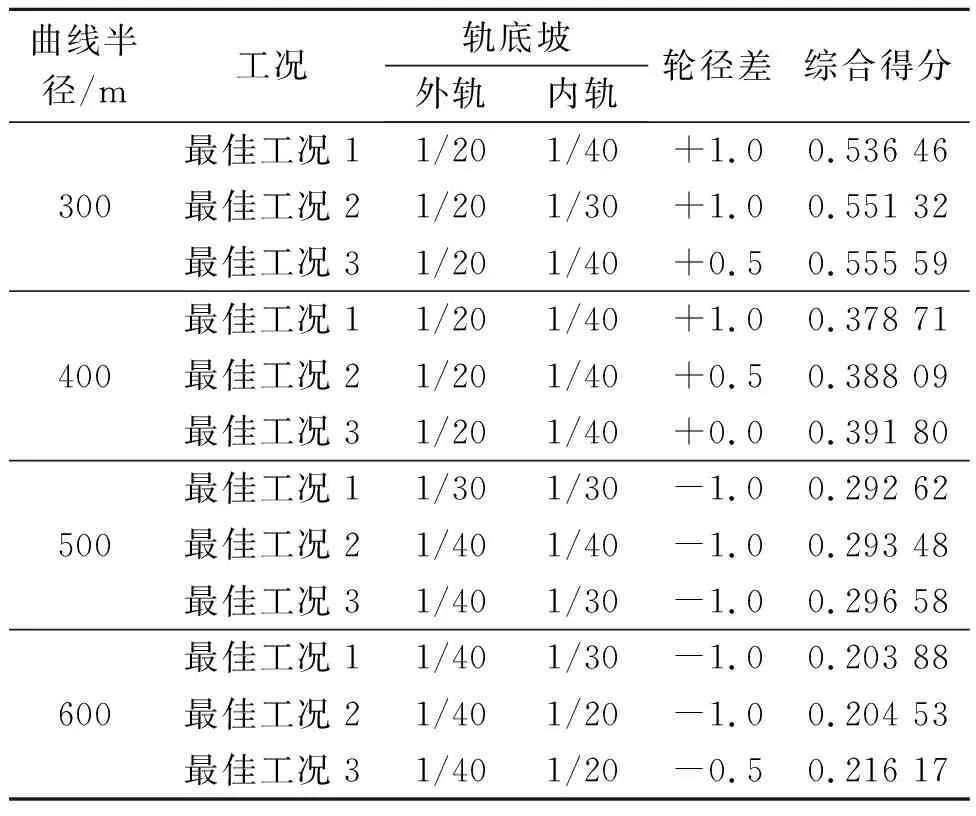
表6 不同曲线半径下综合得分排名

5 结 论

笔者建立了地铁车辆动力学模型,设置了9种轨底坡和5种轮径差工况,分析了在4种曲线半径条件下轮轨横向力、轮对横移量、脱轨系数、轮重减载率和轮轨磨耗指数的变化规律,通过熵权法对上述指标进行加权求和,得到不同曲线半径、不同耦合工况下地铁车辆动力学性能综合得分,从而得出不同曲线半径下轨底坡与轮径差的最佳匹配,具体结论如下:1) 随着曲线半径的增大,轮径差和轨底坡变化对轮轨横向力、轮对横移量和脱轨系数的影响程度越来越大,而对轮轨磨耗指数的影响越来越小。当轨底坡一定时,轮径差从-1 mm变化至1 mm,脱轨系数、轮轨横向力和轮对横移量均逐渐变大,而轮轨磨耗指数逐渐变小;当轮径差恒定且内轨轨底坡不变时,随着外轨轨底坡的增大,轮轨横向力、轮对横移量和脱轨系数逐渐变大而轮轨磨耗指数逐渐变小;轮径差和轨底坡耦合工况对轮重减载率影响不明显。2) 当轨底坡和轮径差工况不变时,随着曲线半径的增大,综合得分逐渐降低,即车辆动力学综合性能逐渐改善。当轨底坡工况一定时,轮径差从-1 mm变化至1 mm,曲线半径300,400 m对应的车辆动力学综合性能逐渐增加;而曲线半径500,600 m对应的车辆动力学综合性能逐渐减小。当轮径差工况一定时,内轨轨底坡不变,外轨轨底坡逐渐变大,曲线半径300,400 m对应的车辆动力学综合性能逐渐增加,而曲线半径500,600 m对应的车辆动力学综合性能逐渐减小。3) 在半径曲线为300,400 m条件下,当外轨轮径小于内轨轮径且外轨轨底坡大于内轨轨底坡时,车辆动力学综合性能最优;而在曲线半径为500,600 m条件下,当外轨轮径大于内轨轮径且外轨轨底坡小于内轨轨底坡时,车辆动力学综合性能最优。以车辆动力学性能综合评价为依据,在曲线半径为300,400,500,600 m 4种工况下,外轨轨底坡、内轨轨底坡和轮径差最优匹配方案分别为(1/20,1/40,+1),(1/20,1/40,+1),(1/30,1/30,-1),(1/40,1/30,-1)。研究结果可为不同曲线半径线路下轨底坡和轮径差的设置提供一定的技术支持,在实际应用过程中,可以根据线路的轨底坡状态对车轮镟修进行指导。

本文得到了北京建筑大学研究生创新项目(PG2022133)的支持。