基于LightGBM算法的海洋土压缩参数预测模型
2024-01-18汪明元王振红陈松庭
汪明元,王振红,陈松庭
(1.浙江华东建设工程有限公司,浙江 杭州 310014;2.中国电建集团华东勘测设计研究院有限公司,浙江 杭州 311122;3.浙江工业大学 土木工程学院,浙江 杭州 310023)
随着施工技术的发展,各类海洋工程建设不断推进。对海洋土体物理力学性质的研究已经成为海洋工程实践中的重要问题。目前,土体的力学性质和设计参数的数值几乎完全依赖于原位土工试验(如取样、钻孔与灌入测试)以及后续的室内土工试验(由固结试验、三轴试验直接得到的各试验土样的压缩性和抗剪强度指标)。然而海洋岩土工程试验成本高昂,针对特定工程展开数量多、密度大的现场试验难度较大,难以获得各位置的土体参数,限制了海洋工程的开展。因此,构建高效、可靠的土体参数预测模型对海洋岩土工程的发展具有重要意义[1]。机器学习算法[2]的兴起与发展促进了计算机技术与传统工程的交叉发展,许多机器学习方法在岩土工程领域已崭露头角[3-4],包括随机森林[5-6]、神经网络[7-9]等,弥补了传统算法表达能力不足、准确率低的缺陷。2017年,Ke等[10]提出的LightGBM作为一种运行速度快、内存占用低的算法,目前已经被广泛应用于电力电气[11]、医疗卫生[12]和轨道交通[13-14]等领域,并已被逐渐应用于岩土工程领域。张凯等[15]建立了基于LightGBM算法的边坡稳定性预测模型,将一些重要的土体参数作为模型的输入,将边坡稳定性作为模型的输出;巫崇智[16]利用LightGBM算法构建了黏性土的不排水抗剪强度预测模型,并分析了贝叶斯调参对预测结果的影响,一定程度上推动了LightGBM算法在岩土工程领域的发展。然而现有研究主要针对稳定性和强度参数,针对变形参数的研究仍比较缺乏。
笔者提出的基于LightGBM算法的海洋土变形参数预测模型可以通过较易获得的土体力学参数来预测较难获得的土体压缩参数。通过贝叶斯调参及k折(k-fold)交叉分析方法对模型进行调整,使模型获得更好的预测性能。该模型有利于降低海洋土体勘察成本,提高土体参数勘察效率。
1 算法原理及实施流程
1.1 LightGBM算法原理
LightGBM作为一种高效实现的基于梯度提升决策树(Gradient boosting decision tree,GBDT)的算法,其工作原理与GBDT类似。该方法通过利用损失函数的负梯度来近似当前决策树的残差值,并将其用于拟合新的决策树。在每次迭代中,模型保持不变,将新的函数添加到模型中以不断减少预测值与实测值的差异[17]。
训练的目标函数为
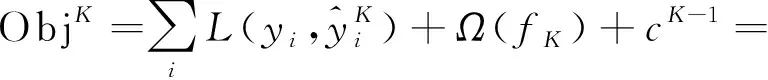
(1)
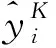
用gi记作第i个样本损失函数的一阶导数,hi记作第i个样本损失函数的二阶导数,目标函数二次泰勒展开的结果为
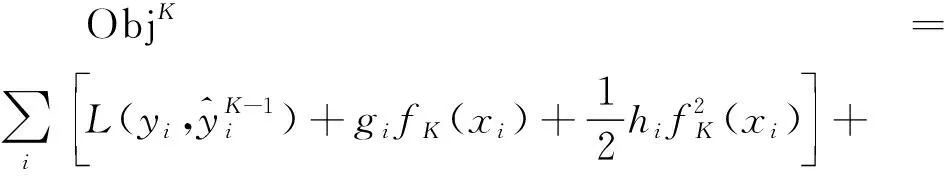
(2)
相较于大多数GBDT算法采用的按层生长的生长策略,LightGBM算法采用了按叶生长的生长策略,即从所有叶中找出信息增益最大的节点进行学习,同时采用max_depth超参数来限制树的深度,防止出现过拟合。LightGBM算法还采用了单边梯度和随机抽样的方法,保留梯度较大的实例,同时对梯度较小的实例进行随机抽样,这种做法可以使用更少的数据量获得准确的估计。同时采用互斥特征合并技术,将一定冲突比率内互斥的特征进行合并,从减少特征的角度达到降维的效果,且不会造成信息丢失[17]。
1.2 模型实施流程
采用python语言建立基于LightGBM算法的海洋土压缩参数预测模型,具体实施流程如下:1) 收集土体参数数据,包括样底深度、含水率、湿密度、土粒相对密度、液塑限、压缩系数和压缩模量等;2) 对数据进行预处理,主要是对缺失参数进行补充;3) 将数据划分为训练集和测试集,在训练集上进行k折交叉验证;4) 将处理好的数据输入LightGBM预测模型中,为模型设置需要调试的超参,训练模型并预测目标参数;5) 通过贝叶斯优化寻找令评价指标达到最优的超参,通过模型准确率评价指标来评价预测结果是否满足要求;6) 得出最终土体参数预测模型。
2 模型构建与应用
以某海上风电场项目获取的共482组土工试验数据作为研究对象,根据土体物理力学参数,建立LightGBM预测模型,预测土体的变形相关参数,即压缩系数和压缩模量,并与实测值进行对比验证,通过贝叶斯调参获得最优超参数,结合多个评价指标定量评估所构建模型的实际预测效果。
2.1 数据准备
收集了共482组土体参数特征,包括样底深度D、土分类名称、含水率W0、湿密度ρ、干密度ρd、土粒相对密度Gs、孔隙比e、饱和度Sr、液限WL、塑限WP、液性指数IP、塑性指数IL、压缩系数av和压缩模量Es等。其中压缩系数av、压缩模量Es根据压缩(固结)试验得到的100,200 kPa的固结压力计算所得。现有液限有2种取值方式:以《土工试验方法标准》(GB/T 50123—2019)规定的圆锥入土深度为17 mm处相应含水率为液限;以《建筑地基基础设计规范》规定的圆锥入土深度为10 m处相应含水率为液限。由于试验值用作基础设计,在本研究中液限指圆锥入土深度为10 m处相应含水率。由于土分类名称是由液塑性指数得出的,而液塑性指数可以通过液限、塑限与含水率计算所得。孔隙率、干密度和饱和度均能通过其他土体参数(含水率、湿密度、土粒相对密度)计算所得。因此在这个预测模型中选取的特征为样底深度D、含水率W0、湿密度ρ、土粒相对密度Gs、液限WL、塑限WP、压缩系数av和压缩模量Es。具体参数特征如表1所示,参数分布如图1所示。由图1可以看出:压缩系数av与压缩模量Es在数值较小时频率较高,数值较大时频率较低。

图1 各土体参数频率直方图Fig.1 Frequency histogram of soil parameters
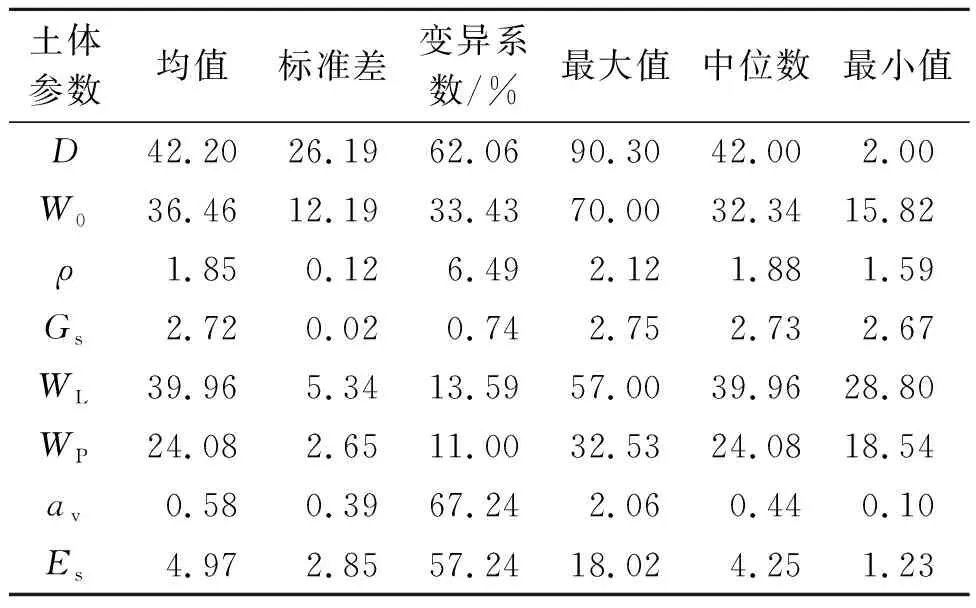
表1 土体参数基本统计特征
采用Spearman相关性分析方法对土体参数数据进行分析。选用两组土体参数为变量,相关系数为-1~1,其计算式为
(3)
式中:di为第i组两种参数等级之差;n为样本组数。
各个土体参数之间的相关系数热力图如图2所示。从图2可以直观感受到各个土体参数之间的关系。Smith[18]提出了关于rs的以下标准:|rs|≥0.8代表两组参数之间相关性很强;0.8>|rs|≥0.5代表两组参数之间相关性一般;0.5>|rs|代表两组参数之间相关性较弱。
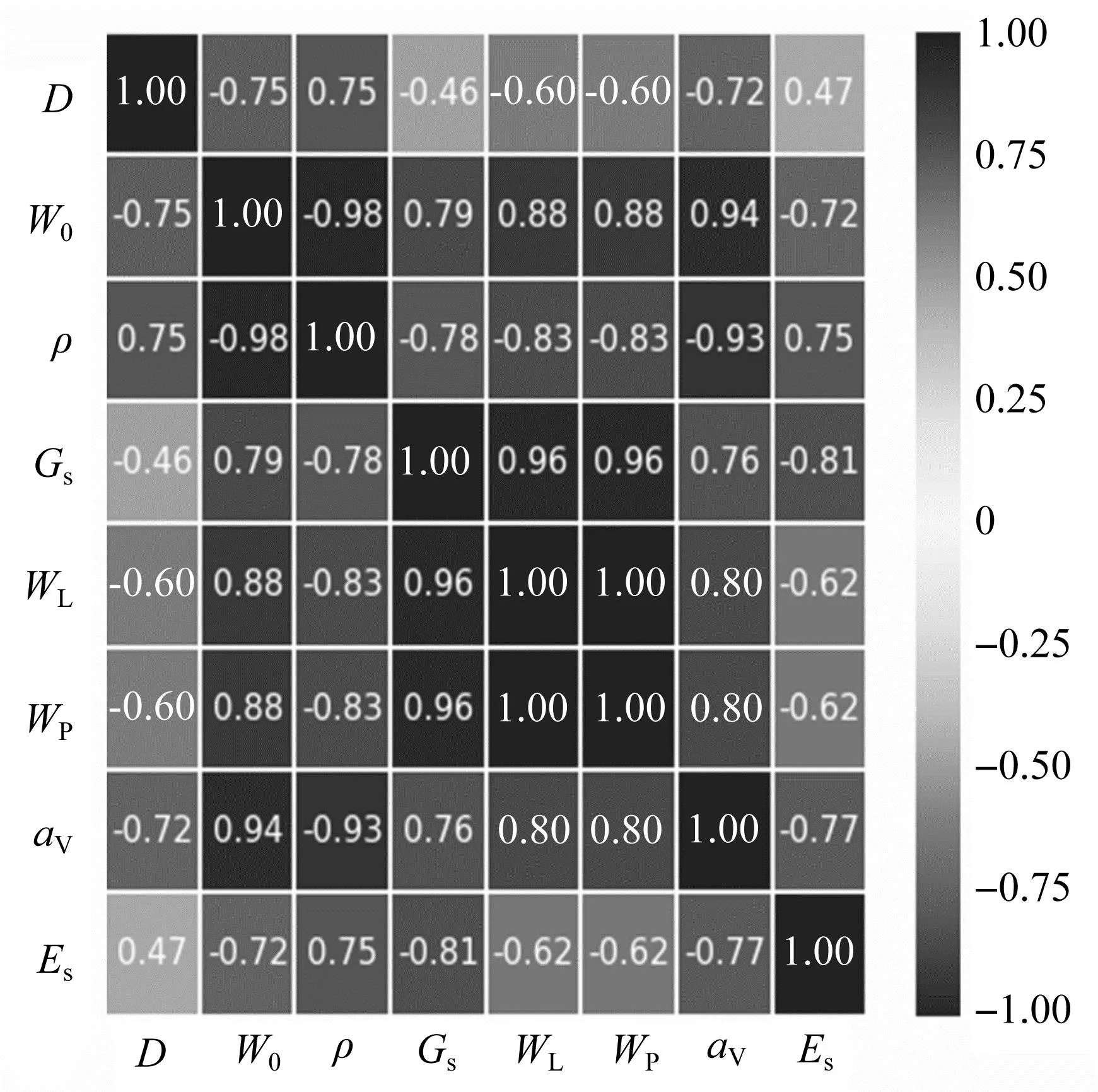
图2 各个土体参数的相关系数热力图Fig.2 Spearman correlation coefficient heat map of each soil parameter
由图2可知:Es与Gs,av与W0,av与WL,av与WP,av与ρ的相关系数绝对值≥0.8,说明Gs对于目标变量Es有较强的相关性,压缩系数av与多数变量有较强相关性,其中压缩系数av与含水率W0的相关系数为0.94,其原因可能是对于饱和土来说,在100~200 kPa的固结压力下,其压缩主要是由于孔隙水的排出,故压缩参数主要与含水率有关。Es与D,Es与W0,Es与ρ,Es与WL,Es与WP,Es与av,av与D,av与Gs的相关系数的绝对值为0.5~0.8,上述9组参数之间有一般强度的相关性。相关性分析为数据处理提供了部分参考依据。
各个土体参数的成分对比如图3所示,当横坐标与纵坐标为相同的特征时,显示该变量自身的分布图;当横纵坐标为不同的特征时,显示两个特征的散点图。从图3中可以直观地看到:av与D,ρ,Es有很明显的负相关性,与W0有明显的正相关性,与Gs、WL,WP有不太明显的正相关性;Es与各土体参数相关性和av与各土体参数相关性相反。
2.2 数据预处理
根据2.1节所提到的参数形成统一的数据集。采用info函数对数据集进行检查,一共有4 520个数据。其中ρ,Gs,av,Es均缺少两组数据,经过观察数据集发现缺少数据来源于同两组土体,故直接删除这两组土体数据。而液限WL、塑限WP的缺失率均为22.3%,直接删除对数据浪费较大。LightGBM算法能够在有缺失值的情况下进行预测,通过对比不进行处理和采用以平均值39.96,24.08对数据进行填充的预测效果,发现两种方式准确性差别不大,故决定不对液限WL、塑限WP进行处理。具体缺失值处理方式如表2所示。

表2 土体参数缺失值以及预处理方式
2.3 LightGBM算法及超参数确定
计算机处理器型号为IntelE5-2670、内存为16 G、操作系统为Windows 10。将预处理后的数据集按照4∶1的比例随机划分为训练集与测试集,其中训练集用于构建模型,测试集用来对模型的实际预测能力进行验证。训练集由384组样本构成,测试集由96组样本构成。
超参数取值对LightGBM的预测效果起到重要作用[19],笔者对max_depth,num_leaves,learning_rate,bagging_fraction,feature_fraction 5个超参数进行研究。其中:max_depth表示树模型的最大深度,通过调整此参数控制树自身深度,防止过拟合;num_leaves表示一颗树上节点的个数,与max_depth一起决定树的形状;learning_rate表示学习率,代表学习过程中的步长,学习率较小时模型性能虽然较稳定,但运算量较大,处理时间长;bagging_fraction表示采用数在整个模型中的比例,当取值较低时可以防止过拟合;feature_fraction用于控制其他参数中的分裂点,防止过拟合。模型参数的选择如表3所示,其余参数按照默认值取值。

表3 模型参数设置
2.4 k折交叉验证
由于笔者所选用的数据量相对较少,如果仅仅将数据集分为训练集和测试集,划分的偶然性会影响训练结果。k折交叉验证就是将原数据集中的训练集进一步划分成大小一致的k个集合。选择其中一个集合作为验证集,其余k-1个集合作为训练集进行训练,将这个训练步骤重复k次。选取令k次建模中的误差平均值达到最小时的超参数作为最终超参数,在原始的全体训练集上进行训练。在k折交叉验证方法中,k一般取5~10。由于本研究的数据量较少,计算压力小,为了得到较好的计算结果,决定采用10折交叉验证对所建模型进行验证。由于LightGBM可以直接调用cv函数对数据进行交叉分析,故将最大迭代次数设为500,早停轮数设为20,以保证整个数据集能够进行充分训练。
2.5 模型准确率评价指标
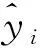
平均绝对误差MAE是预测值和实测值差的绝对值的平均值,范围为0~+∞,预测值越接近于真实值,模型越精确,MAE值越低,其计算式为
(4)
均方根误差RMSE是预测值和实测值之间平方差的平均值,范围为0~+∞,预测值越接近于真实值,模型越精确,RMSE值越低,其计算式为
(5)
平均绝对百分比误差MAPE是可以反映预测值与实测值误差占实测值的百分比的平均值,范围为0~+∞,预测值越接近于真实值,模型越精确,MAPE值越低,其计算式为
(6)
决定系数R2的计算式为
(7)
2.6 贝叶斯优化
在选用超参数的值时,虽然可以选择不断调参来获得使评价指标最理想的超参数值,但评估每一个点的成本很高。而选用贝叶斯优化不需要评估每个点,只需要为每个超参值提供一个区域,这种调参方式会搜索使目标函数达到最优值时各个超参数的值。相较于穷举搜索与随机搜索等其他优化方式,贝叶斯优化重复次数少,可以同时为多个参数调参,运行速度快,内存占用小。
为2.3节中选用的5个参数设置调参范围,选择RMSE作为评价指标,通过贝叶斯优化调参不断迭代得到更低的RMSE准确率评价值,用贝叶斯调参获得的超参数来建立准确性最高的模型。由于数据量不多,选用调参参数量和范围不大,为保证优化全面性,尽量做到充分调参,将最大评估次数设置为200,总消耗时长分别为850,1 277 s,最终调参结果如表4,5所示。

表4 对于压缩系数av的LightGBM贝叶斯超参数调参结果

表5 对于压缩模量ES的LightGBM贝叶斯超参数调参结果
为了进一步对本研究中所给的基于LightGBM的土体参数预测模型的预测能力进行评估,将所建模型与未进行k折交叉验证和贝叶斯调参的模型进行对比。在前文的参数选择中剔除了干密度ρd、孔隙比e、饱和度Sr、液性指数IP和塑性指数IL这5个可以通过已选取的特征计算出来的人工特征。为了探究建模中人工特征对数据准确性的影响,同时将样底深度D、含水率W0、湿密度ρ、干密度ρd、土粒相对密度Gs、孔隙比e、饱和度Sr、液限WL、塑限WP、液性指数IP、塑性指数IL和压缩系数av、压缩模量Es作为特征进行建模,不同模型的准确性评价指标如表6所示。

表6 不同模型的准确性评价指标
由表6可知:在采用不同模型对相同数据集进行处理时,笔者所建模型相较未进行k折交叉验证和贝叶斯调参的模型有一定提升。相较加入人工特征后的模型,笔者模型的预测准确性差异不明显,说明在建模中加入人工特征对最终预测结果的准确性并没有提升。
在10折交叉验证下所构建的基于LightGBM算法的模型在MAE,R2,RMSE,MAPE 4种评价指标下的表现如图4所示。针对av与Es的准确性评价指标,R2与RMSE的准确性排序是一样的,两者存在负相关,而这两种指标与MAE和MAPE指标的准确度排序不一样,说明相同数据的不同评价指标准确度的排序并不相同。不同折数对av各个准确性指标的影响无明显规律性;随着折数的变多,对Es预测的准确性振荡变优。
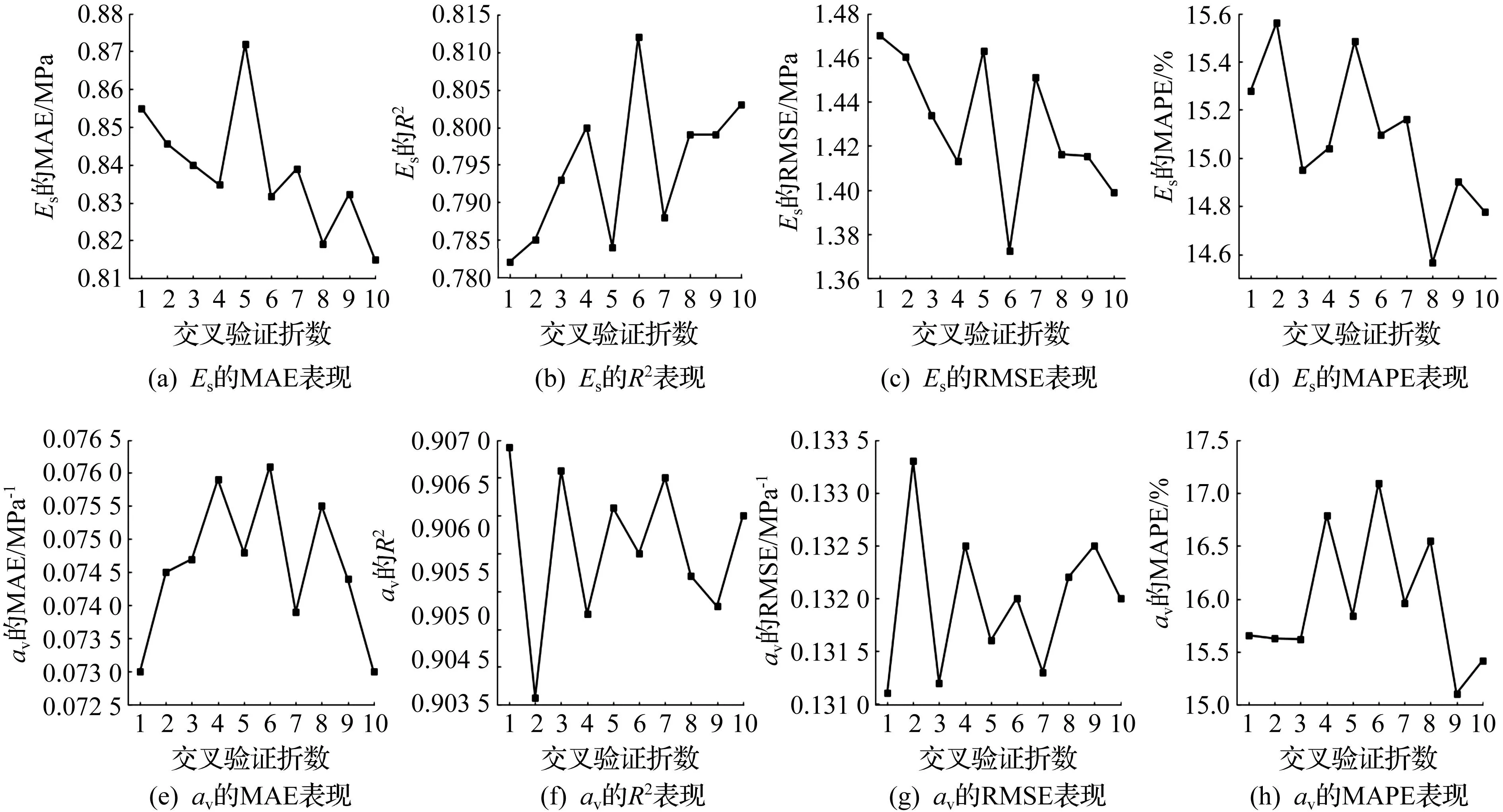
图4 模型在不同交叉验证折数中4种评价指标的表现Fig.4 The model performance on four evaluation indicators in different cross-validation folds
模型预测值与实测值的对比如图5所示。由图5可知:在土体参数数值较小时,预测值与实测值差别较小;在数值较大时预测值和实测值差距逐渐变大。可能是由于较小的数据数量较多,模型能进行充分学习,从而提高模拟准确性,总体来说本模型对两种土体压缩参数预测准确性较高。通过比较图2中的压缩系数av、压缩模量Es和其他各个土体参数间的相关系数,可以发现av与D,W0,ρ,WL,WP的相关系数绝对值均大于Es与这些参数的相关系数,仅与Gs的相关系数稍小。从图5可以看出:av的预测准确性高于Es,说明土的力学参数与物理参数相关性越高,预测的准确性越高。
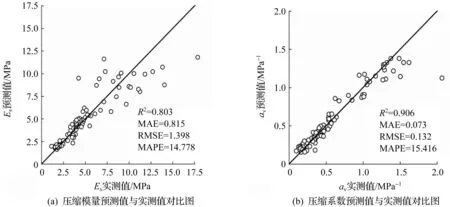
图5 模型预测值与实测值对比图Fig.5 Comparison of model predicted value and measured value
3 结 论
笔者提出了一种基于LightGBM算法的土体参数预测模型,该模型能够通过一些便于获得的土体物理性质参数预测难以获得的变形参数,即压缩系数av、压缩模量Es。采用k折交叉验证法和贝叶斯调参对模型超参数进行优化。通过准确性评价指标判断了该模型预测的准确性,并分析了k折次数、人工特征、数据集数量、预测量与输入特征相关性等因素对模型准确性的影响。结果表明:贝叶斯调参一定程度上能够提高预测准确性;k折次数的增加使Es预测的准确性振荡变优;建模时加入人工特征对最终预测结果影响不明显;数据集越大、预测指标与特征值相关性越高,模型预测准确性越高。该模型对压缩模量Es的R2评价指标为0.803,对压缩系数av的R2评价指标为0.906,预测准确性较高,研究结果可以为确定海洋土土体变形参数提供参考。
