基于高斯似然的精准水声信道估计

杨 光, 乔培玥, 梁俊燕, 秦正昌, 巩小东, 倪秀辉

(1. 青岛理工大学信息与控制工程学院青岛市水声通信及探测装备技术创新中心, 山东 青岛 266525;2. 南洋理工大学电气与电子工程学院, 新加坡 639798; 3. 山东省科学院海洋仪器仪表研究所,山东 青岛 266318; 4. 乌克兰国立技术大学(基辅工学院), 乌克兰 基辅 03056)

0 引 言

近年来,随着海洋资源的开发以及海上军事行动的需要,基于水声信道进行数据信息传输的需求越来越迫切。因此,水声通信技术得到了快速发展和广泛应用。然而,水声信道具有时变多途强和稳定性差的特性,使得接收信号发生畸变,造成水声通信系统解码性能降低甚至失效[1-2]。

当前信道估计算法主要有3大类:盲估计算法、半盲估计算法和基于参考信号(导频或训练序列)的信道估计算法。盲估计算法需要大量的数据累积,因此它的计算复杂度高、灵活性差[3];半盲估计算法可能会出现传播失真的问题,运算量较大且收敛速度较慢[4]。与以上两类算法相比,基于参考信号的信道估计算法跟踪能力和估计能力较强[5-9],且计算复杂度较低,因此本文采用了基于参考信号的信道估计算法。

针对水声信道估计问题,国内外多所研究机构进行了大量的研究。国外,康涅狄格大学提出一种稀疏信道估计模型,采用正交匹配追踪和基追踪算法,显著提高系统的性能[10]。麻省理工学院提出一种基于多径传播的稀疏信道估计算法,利用接收信道之间的空间相关性,减少信道估计器的数量,降低计算复杂度[11]。国内,哈尔滨工程大学提出基于基追踪去噪的稀疏信道估计算法,后来又提出一种基于稀疏约束和最大似然的自干扰信道估计算法,具有更快的收敛速度和更高的估计精度[12-13]。厦门大学提出一种适用于长时延扩展水声信道的联合稀疏恢复估计算法,将长时延信道估计问题转化为联合稀疏恢复估计问题,以减少训练序列的开销,提高信道估计的准确性[14];随后,又提出一种分布式压缩感知算法,利用同相正交匹配追踪算法对模型进行优化,提高信道估计性能[15]。浙江大学提出一种适用于单载波、多输入多输出(multiple-input multiple-output,MIMO)的水声通信鲁棒接收机方案,该方案采用稀疏贝叶斯学习算法,具有较低的计算复杂度[16]。中国科学院声学研究所提出近似稀疏信道估计算法,将压缩感知技术引入单载波频域均衡(single-carrier frequency domain equalization,SC-FDE)系统,准确高效实现了稀疏信道估计[17]。然而以上算法均采用传统的时分复用训练方案,快变信道估计性能会降低。为了进一步提高时变水声信道的估计和跟踪能力,伍伦贡大学、西澳大学和青岛理工大学联合提出了一种基于叠加训练(superimposed training,ST)方案的水声通信算法[18-24],将训练序列和符号序列线性叠加,使得训练序列和符号序列信道信息完全一致。因为训练序列持续发送,所以可以实现时变水声信道的实时跟踪。

为了充分发挥ST方案的潜力,基于文献[18-24],提出了一种基于高斯似然(Gaussian likelihood,GL)的信道估计算法。该算法以一种简化的高斯乘积方式实现了与文献[18]和文献[22]相同的信道估计和跟踪性能。GL算法将各短块的信道估计误差的高斯概率密度函数相乘,得到的函数仍然服从高斯分布,且方差变小,从而极大提高了每个短块的信道估计性能。将信道估计嵌入到Turbo均衡中[25-32],均衡器和译码器以迭代的方式进行信息交换,实现了对每个短块的精准信道估计。最后,通过仿真和海上运动实装试验验证了GL算法的有效性。

1 基于ST方案和GL的水声信道估计

1.1 基于ST方案的信道估计

yn=Hnsn+w=Hn(rtLn+fn)+w=Hnfn+rHntLn+w

(1)

定义hn、fn、tn、sn分别表示信道冲激响应Hn、符号序列fn、周期训练序列tLn和叠加训练序列sn中的一个元素。当r为常数时,叠加训练序列的一个元素sn=r×tn+fn,因此接收信号的一个元素可以表示为

(2)

式中:*表示卷积运算;wn表示高斯白噪声;N表示信道长度。假设符号序列的均值为0,且T≥N,可得

(3)

将E[yn]分成p个短块,即

(4)

(5)

其中i=1,2,…,p。采用周期训练序列,可以得到一个T×N的Toeplitz矩阵A,即:

(6)

对E[yiT]进行累加求和计算,当p为无穷大时,可得

(7)

当T≥N时,基于最小二乘(least square, LS)算法,信道估计值可表示为

(8)

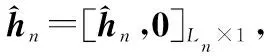
1.2 基于GL的精准信道估计

信道估计的误差可以用两个独立同分布的高斯概率密度函数表示,其中均值表示信道估计值,方差表示信道估计的误差,其误差可以用高斯分布进行刻画[18,22]。定义第n个短块和第n+1个短块的高斯概率密度函数分别为pn(x)和pn+1(x),即:

(9)

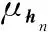
将两个高斯概率密度函数相乘,可得

(10)

对其进行展开计算,可得

(11)

(12)

可以看到乘积后的方差变小,即乘积后的信道估计更加准确。根据式(11),可得乘积后的高斯分布:

(13)

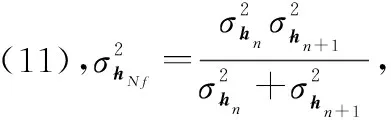
(14)

(15)

整理可得

(16)

和

(17)

图1 第n个短块的信道估计Fig.1 Channel estimation of the nth segment

1.3 训练干扰消除、噪声功率估计和基于虚拟训练序列的信道估计性能提升

(18)

(19)

(20)

以第n个短块的线性最小均方误差(linear minimum mean squared error, LMMSE)均衡为例。基于文献[22-24],可得符号的先验、后验、外均值和方差为

(21)

将信道估计和均衡以Turbo均衡的方式进行迭代计算。对每个数据块进行迭代计算,迭代过程如图2所示。

图2 迭代计算Fig.2 Iterative calculation

(22)

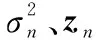
信道估计的计算量级为每抽头平方级,幸运的是,信道均衡的计算量级仅为每符号对数级。因此,Turbo均衡迭代计算过程中的计算复杂度主要由信道估计决定。当信道阶数较短时,总的计算量较小,可实时处理;当信道阶数较大时,比如高达几百个抽头时,实时处理难度较大。在实际工程中,可将信道能量的主要部分取出,求得近似信道估计,这可极大降低计算量,达到实时处理。

2 计算机仿真与实装试验

2.1 计算机仿真

为了验证GL算法的有效性,对其进行计算机仿真,其参数如表1所示。其中,SINR为信干噪比(signal to interference plus noise ratio,SINR)。采用1/4码率的卷积码,训练序列与符号序列的功率比为0.25∶1,将1个数据块分成不同长度的短块,根据所含信息比特的不同,将不同长度的短块定义为S128、S256、S512和W1024。采用QPSK映射和基带通信,带宽为4 kHz。

表1 仿真和试验参数Table 1 Parameters of simulations and experiments

接收信号结构如图3所示。

图3 接收信号结构 Fig.3 Structure of the received signal

图3中1帧数据包含60个短块,每个数据块包含512 bits,每个数据块分成多个256符号短块或512符号短块,每个短块均添加循环前缀(cyclic prefix, CP)作为保护间隔,CP长度为128个符号。采用正负调制率的双曲调频信号(hyperbolic frequency modulation, HFM)作为帧头和帧尾。静态水声信道的脉冲响应如图4(a)所示,将其经过0次和1次迭代之后的信道与真实信道作对比,如图4(b)所示。迭代0次的信道与真实信道的脉冲响应相差较大,而经过1次迭代之后的信道与真实信道的脉冲响应几乎完全一致,即经过1次迭代后的信道基本接近于真实信道。对未使用GL算法和使用GL算法的系统进行误码率性能测试,测试结果分别如图5(a)和图5(b)所示,横轴表示迭代次数,纵轴表示误码率。从图5(a)可看出,未使用GL算法的系统,不同长度短块的误码率性能相差较大,无法正常工作;从图5(b)可看出,使用GL算法可以获得全局精准信道估计,经过多次迭代后,不同长度的短块误码性能几乎相同,验证了GL算法的有效性。

图4 水声信道Fig.4 Underwater acoustic channel

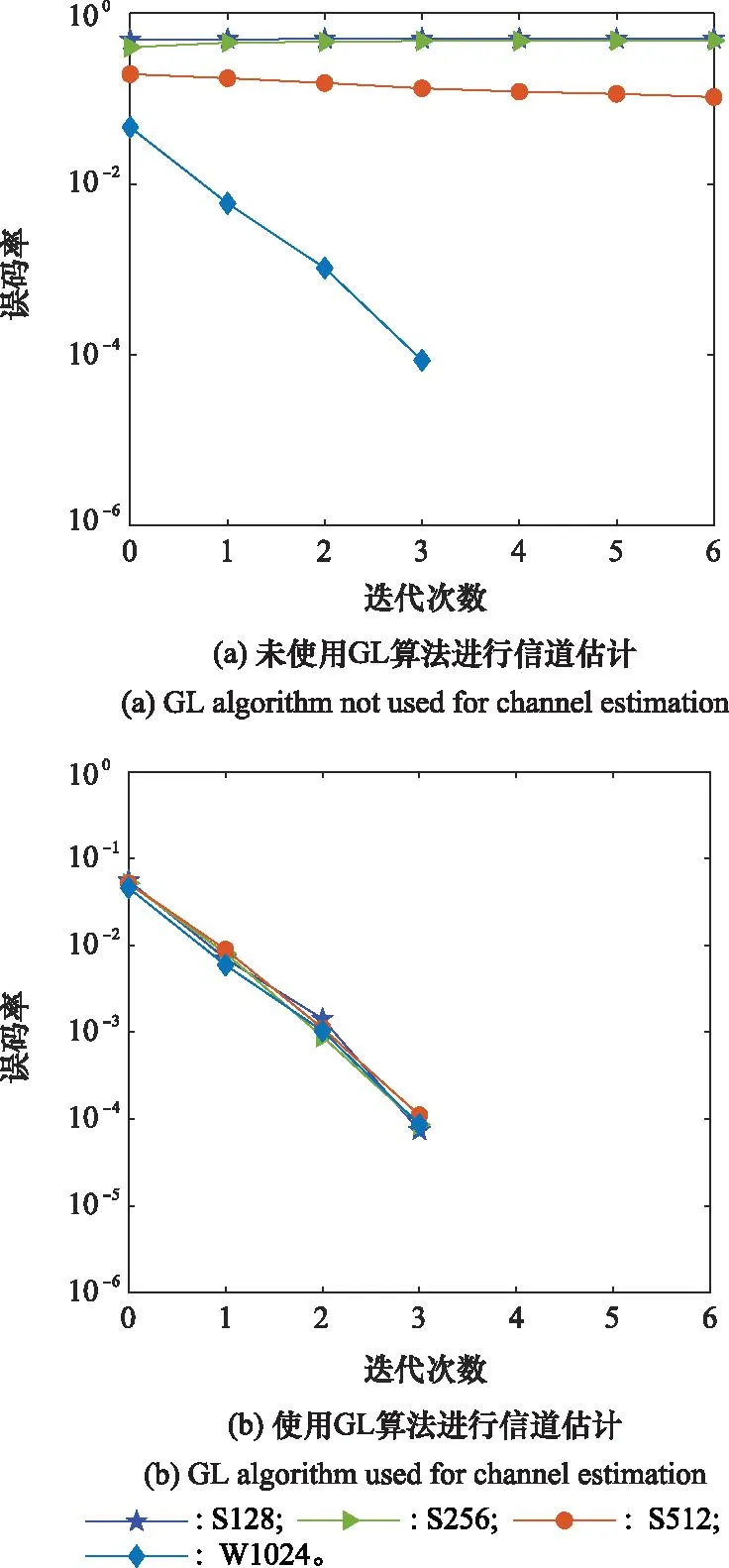
图5 不同长度短块的误码性能对比Fig.5 Bit error performance comparison of segments with different lengths

以S256为例,当编码速率为1/4时,分析在不同的SINR下,均方误差和误码率的变化情况,分别取SINR为10 dB、12 dB、14 dB和16 dB。从图6(a)可看出,当SINR越大时,系统的均方误差越小,从图6(b)可看出,随着迭代次数和SINR的增大,系统的误码率随之降低。当SINR=16 dB时,经过1次迭代之后,所有信息比特全部正确解码。

2.2 500 m短途实装运动通信试验(2 m/s)

在胶州湾进行了收发节点相距500 m的短途实装运动通信试验。试验参数和试验布放分别如表1和图7所示,换能器布放深度为4 m,水听器布放深度为5 m。试验中采用1/8码率的卷积码,训练序列和符号的功率比为0.25∶1。CP长度为16个符号。系统采用QPSK映射和同相正交调制(in-phase quadrature, IQ),中心频率为12 kHz,采用带通滤波,采样频率96 kHz。

图7 胶州湾试验Fig.7 Experiments in Jiaozhou Bay

发射船以2 m/s的速度离开接收船,接收信号的SINR为14 dB,带宽为4 kHz。试验所用实装水声通信机的示意及尺寸如图8和图9所示,参数如表2所示。在实装水声通信机中插入SD卡,利用接收机采集数据,用计算机对采集的数据进行分析。

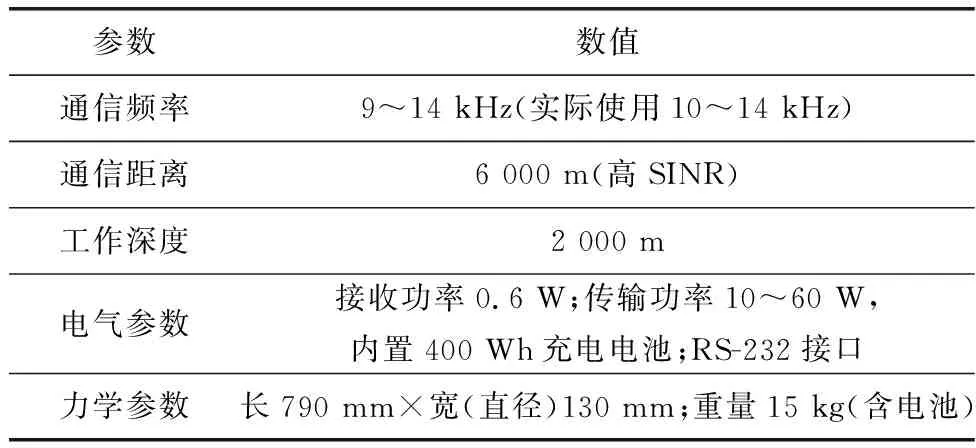
表2 实装水声通信机参数(Seatrix Modem)Table 2 Parameter list of underwater acoustic communication machine (Seatrix Modem)

图8 实装水声通信机(Seatrix Modem)Fig.8 Illustration of underwater acoustic communication machine (Seatrix Modem)

图9 水声通信机尺寸(Seatrix Modem)Fig.9 Dimension of underwater acoustic communication machine (Seatrix Modem)

用“#11”表示第11块数据,1帧数据包含16个短块。当短块长度为256个符号时,信道如图10所示,4个短块的信道存在明显差异,说明水声信道是时变的。

定义α为相关系数,当α=0、α=auto和α=1时,对系统的误码性能进行比较。从图11可看出,当α=auto时,经过1次迭代后,星座点达到理想聚合,所有信息比特全部正确解码。16个短块在不同α下系统的误码率性能如表3所示,可看出,当α=auto时,经过1次迭代,系统的BER最低,验证了所提算法的有效性。

表3 不同相关系数下GL算法的误码率性能(通信距离为500 m,相对速度为2 m/s)Table 3 Bit error rate performance of GL algorithm with different correlation coefficients (the communication distance is about 500 m, and the relative speed is about 2 m/s)

图11 不同相关系数下的星座图Fig.11 Constellations with different correlation coefficients

2.3 5.5 km长途实装运动通信试验(0.5 m/s)

在胶州湾进行了收发节点相距5.5 km的长途实装运动通信试验。发射船以0.5 m/s的速度离开接收船,接收信号的SINR为14 dB。试验参数和试验布放分别如表1和图12所示。试验采用1/4码率的卷积码,训练序列和符号的功率比为0.25∶1。1帧数据包含16个短块,每个数据块包含512 bits,中心频率为12 kHz。系统采用带通滤波,带宽为4 kHz,采样频率为96 kHz。

图12 长途运动通信试验布放Fig.12 Experimental deployment moving communication with a long distance

以第3块为例,当短块长度为256个符号时,信道估计和星座点聚合如图13所示。图13(a)为4个相邻短块的信道估计,横轴表示抽头,纵轴表示幅度,4个短块存在明显差异,说明水声信道是时变的。图13(b)可看出,经过2次迭代后,星座点达到理想聚合,所有的信息比特全部正确解码。图14为第12块数据的信道估计和均衡结果,当迭代2次后,星座点达到理想聚合,所有信息比特全部正确解码,验证了GL算法的有效性。

图13 信道估计和星座图Fig.13 Channel estimates and constellations

图14 信道估计和星座图Fig.14 Channel estimates and constellations

通过设置不同的相关系数α,对系统的误码性能进行比较。从表4可看出,当α=auto时,经过1次迭代后,16块数据的信息比特全部正确解码,验证了GL算法的有效性。

表4 不同相关系数下GL算法的误码率性能(通信距离为5.5 km,相对速度为0.5 m/s)Table 4 Bit error rate performance of GL algorithm with different correlation coefficients (the communication distance is about 5.5 km, and the relative speed is about 0.5 m/s) %

3 结 论

提出的基于GL的精准水声信道估计算法,实现了信道的分短块连接,从而达到时变水声信道的精准估计。采用ST方案,提高了时变水声信道的估计和跟踪性能。每个短块的信道估计误差都可以用高斯分布来刻画,多短块的高斯分布乘积仍然为高斯分布,乘积后的高斯分布方差变小,信道估计更接近于真实信道值,表明乘积后的信道估计更加准确,相当于利用了整个数据块实现了对每个短块的全局精准信道估计。结合ST方案、GL算法和Turbo均衡,利用均衡器和译码器之间的信息交互,进一步提高了时变水声信道的估计和跟踪性能。最后,通过计算机仿真和胶州湾海上运动实装试验,验证了所提算法的有效性。