间歇式信息传输条件下无人机搜索覆盖规划

曹志强, 张 佳, 辛 斌

(北京理工大学自动化学院, 北京 100081)

0 引 言

单无人机从基站出发开始覆盖环境,并将环境信息实时传递回基站。这种通信保持的方式能够实现高效的信息传输,但是基站通信范围有限。尤其在火灾、地震、救援等场景下,通信设施瘫痪,恢复通信将会花费较长时间,或者依赖于较多硬件设施[1],造成基站等的通信范围大大减少,无人机的运动范围也会受到较大限制。而在间歇式信息传输条件下,无人机在一段时间内不与基站通信,而是覆盖更多的区域,在经过一定时间后返回基站通信范围并将信息传输回基站,之后继续返回覆盖路径,完成剩余覆盖任务,重复以上过程直到信息传输完毕。这种方法可以扩大无人机的工作范围,并使无人机的运动不受通信距离的限制,更加灵活地完成任务。

间歇式信息传输下多智能体协作的核心问题为智能体通信位置和时刻的选取与任务规划的耦合问题,多智能体间若长时间不通信,会导致协作效率下降,若频繁通信则会导致运动自由受限且执行效率下降。

相关学者讨论了间歇式规划下的各种问题,Sabo等[2]在多无人机的PDP(pickup and delivery problem)中使每个无人机到各个位点采集数据,随后返回基站的通信范围反馈信息给基站。为了提高数据收集和反馈的效率,其采用了两阶段的启发式方法,与最优解对比,两种方法最多相差5%,但是其没有考虑障碍物等约束。Kantaros等[3-4]利用了线性时序逻辑(linear-time temporal logic, LTL)对多智能体系统通过间歇性通信完成任务的问题,进行了系统性的研究,但是其更加关注任务执行效率,且只确保有关任务上的协商能够经常进行。而最近Aragues等[5]针对不同速度和通信范围的智能体巡逻一维度环形图各个位点问题,以最小化重访位点时间为目标设计了分布式算法。Scherer等[6]考虑智能体在巡逻过程中将信息通过智能体之间的间歇式通信传输到基站,针对传输时间有界建立了带时间窗的最短路径问题(shortest path problem with time windows, SPPTW)模型。Caraballo等[7]则讨论智能体之间信息传输时间有界。虽然已有上述一些优秀的成果,但是间歇式信息传输下的覆盖规划相关文献依然较少。

全覆盖路径规划常运用的方法是在单元分解后计算各个单元之间的最短覆盖路径。经典的单元分解方法,包括Boustrophedon[8-9]、Trapezoidal分解[10]、莫尔斯分解[11]、聚类分解[12]和单侧区域分割[13]等。Tung等[14]利用直接法 (direct method, DM)优化单元内的遍历路径,利用遗传算法规划各个单元间的覆盖路径。Cai等[15]采用A*算法求解覆盖路径。文献[16-17]利用螺旋卡壳规划 (rotating calipers path planner,RCPP)单元内路径规划方法和蚁群算法规划单元间遍历路径。王伟等[18]利用自适应升温的模拟退火算法优化遍历路径。而从智能体的模型出发,Yuan等[19]考虑无人机在覆盖时的能量限制设置了多个加油站。Theresa等[20]考虑了机器人转弯半径等约束。

针对通信距离约束下的覆盖,诸多文献重点兼顾通信保持与覆盖规划,尹洋等[21]利用改进的K-means++算法划分搜索区域,利用分布式拍卖给每个智能体分配区域。为实现连续通信,多智能体在进行分布式覆盖探索时可以沿着通信拓扑拉普拉斯矩阵第二小特征值减小的逆梯度方向前进[22-24]。王宁等[25]设计了一种能够在通信完全有效、局部有效以及完全失效下切换信息交互方法的信息交互与决策机制,在完成覆盖搜索任务时能够有效兼顾对运动目标的搜索。Banfi[26]在覆盖探索中采用经常性通信连接方法,智能体在完成一定区域覆盖后需要通过多跳通信传递信息给基站。相比Banfi,Benavides等[27]考虑了通信保持与覆盖探索的权衡。Pei等[28]则对通信保持和覆盖问题进行了分解,将其转化为集覆盖问题、Steiner树问题和线性分配问题求解。

上述文献较多地讨论了间歇式通信下的巡逻问题,主要研究了通信保持与覆盖的权衡,对间歇式通信下的覆盖规划问题讨论较少,也没有讨论如何实现间歇式通信与覆盖规划之间的权衡。针对上述问题,本文具有以下创新点。

创新点 1针对间歇式通信与覆盖规划之间的权衡问题,当需要覆盖的目标点较为分散且数量较少时,采用层次聚类方法对点集合进行聚类得到无人机每次从基站出发需要覆盖的路径点集合,在考虑了障碍物影响的情况下,提出了一种新的聚类距离度量方法。

创新点 2针对全区域覆盖问题,相对于创新点1需进一步考虑覆盖路径的质量,要减少路径中转角过大的情况,对此提出一种三阶段的智能优化方法。其思想是先利用文献[17]的覆盖路径求解方法最小化覆盖路径长度,再优化覆盖路径上的返回到基站的位点,实现所有环境位点信息传回基站的时间之和最小化,在降低问题求解复杂度的同时保证求解质量。

创新点 3在优化覆盖路径上的返回到基站的位点时,对目标函数(时间之和)进行分析,确定最优的返回次数搜索范围,进一步遍历得到最优往返次数的取值,此后利用整数编码的遗传算法优化在覆盖路径上的返回位点,实现解空间压缩后的高效求解。

1 问题建模

间歇式信息传输条件指的是:由于无人机在返回到基站的通信范围内时才能传递信息给基站,因此无人机需要往返于待访问目标点和基站之间,这种运动方式形成了间歇信息传输的形式。首先,据此建立间歇式信息传输条件下的覆盖规划模型。

1.1 地理环境建模

以无人机的感知范围半径Rs作为离散化的分度,对待覆盖区域进行离散化,从而实现对于地理环境的栅格化处理,并利用高程地图对其进行描述,高程地图的每个栅格均包含高程信息。

由于环境中时常包含着非结构化的部分,例如不规则的障碍区或禁飞区,另外地理环境对于无人机的运动影响较大,因此需要进一步处理这种非结构化的问题,本文对栅格化后的环境模型进行两次“过滤”处理。

本文中的无人机为小型无人机,考虑到其飞行能力受限,且从安全角度出发,设置其最大飞行高度为hthreshold。若该栅格内障碍高度大于hthreshold,则该栅格被障碍占据,无法通行。

考虑地理环境在二维平面角度非规则形状,如图1所示,采用两种策略进行处理。

图1 环境建模方法Fig.1 Methods of environment modeling

图1为栅格地图,黄色部分为障碍,如图1(a)所示。若栅格中心点C位置处于表示障碍的多边形外,则判定该栅格为自由栅格;否则,如图1(b)所示,判定其为障碍栅格。

1.2 间歇式信息传输下的覆盖规划模型

设无人机的平均移动速度大小为v,无人机初始点在基站。以无人机的感知范围半径Rs作为离散化的分度,对待覆盖区域进行离散化,设环境需要覆盖的位点集合为Tr,Tr={Tr1,Tr2,…,Tre},记作请求点集合,e表示请求点数量,在需要进行区域全覆盖时,其表示所有自由空间(障碍物之外的空间)的请求点数量。当无人机通过运动返回基站通信范围时,将位点信息传回基站。假设Tr1为基站,该问题只返回两次的问题图示如图2所示。

图2 问题图示Fig.2 Illustration of the problem

设无人机从基站Tr1出发沿着黑色实线箭头所示路径覆盖区域内的各个点(以蓝色五角星表示),从点a沿着蓝色虚线路径返回到基站通信范围反馈所得信息,点a称作返回点。之后,无人机从基站沿着红色虚线路径运动到点b,此时点b称作恢复点。无人机继续覆盖完所有区域后从返回点c沿着黄色虚线路径返回基站,完成所有区域覆盖。按照上述流程,覆盖路径按照往返次数,分成了图2中的两段覆盖路径。

该问题的目标是让基站尽快收集环境目标信息。设无人机从任务开始自基站出发到Tri被访问、再到返回基站通信范围且与基站交换Tri信息所用的时间为ti,则目标函数为

(1)

约束条件包括:

zi=1, ∀i∈{1,2,…,e}

(2)

(3)

(4)

(5)

决策变量按此定义:zi表示请求点Tri是否被无人机访问,若为1,则访问,否则为0;pij表示无人机是否从Tri运动到Trj,若为1,则是,否则为0;ui表示无人机是否从Tri回到基站通信范围回馈信息。

约束条件的描述为:式(2)表示每个请求点必须且仅访问一次,无人机需要经常回到Tr1通信范围回馈信息。式(3)确保每个请求点的出度等于入度,从而确保无人机行驶路线的连通性。式(4)表示无人机从Tr1出发开始运动。式(5)表示无人机至少往返于基站通信范围和覆盖路径一次。该问题模型由Sabo等[2]提出,本文将其推广到覆盖问题中。该问题相对于覆盖规划问题的区别在于无人机无法在覆盖过程中与基站通信,需要经常从覆盖区域返回到基站传递信息。核心难点问题和特点在于实现覆盖规划与信息传输的最优权衡。这种区别尤其体现在目标函数上,其不是最小化覆盖路径长度,而是最小化所有位点信息传递回基站的时间,若只在覆盖完所有区域才返回基站,则会增大信息回馈时间。体现在决策变量上,不仅需要规划覆盖,还需要求解间歇式信息传输的时机。

2 问题求解方法

针对覆盖规划问题与返回位点选取问题的耦合问题,求解思路如图3所示。

图3 求解思路Fig.3 Solution idea

先对问题的情形进行分类讨论,若是对区域进行全覆盖,则先执行步骤(a),求解最短覆盖路径。步骤(b)、步骤(c)则以式(1)最小化为目标,优化覆盖路径上的返回到基站的位点;若不是对区域进行全覆盖,即待覆盖位点分散且较少时,则执行步骤(d),对需要覆盖位点进行层次聚类,每个聚类包含无人机每次从基站通信范围出发需要覆盖的所有位点。无人机每次覆盖完这些聚类内的点之后返回基站通信范围。步骤(e)在得到无人机每次需要覆盖的点集合后,需要求解遍历这些点的覆盖路径。显然,覆盖路径的起点为恢复点,终点为返回点。以下在第2.1节中介绍非区域全覆盖的情形,进一步阐释步骤(d)、步骤(e)。第2.2节中讨论区域全覆盖的情形,进一步阐释步骤(a)～步骤(c)。

2.1 非区域全覆盖的情形

在待访问的请求点分布较为分散且数量较少时,Sinaga等[29]为划分得到待搜索任务点使用K-means++聚类的方法,而Sabo等[2]则采用了层次聚类的方法,实验结果良好。本文方法采取的步骤与Sabo等在文献[2]中采用的步骤相同,区别在于聚类时采用的聚类之间的距离度量不同。

首先简要说明Sabo的步骤,其主要的方法步骤为:对请求点进行层次聚类,聚类的度量是两个请求点到基站的欧式距离之比与请求点相对基站方位的夹角,比值越接近1且夹角越接近0,则两个请求点将会优先聚类。按照模糊推理得到唯一的最优聚类次数。模糊推理的参数则利用遗传算法离线学习得到。在聚类完成后,需要利用智能优化方法计算每个聚类内部点遍历的顺序,在得到所有聚类和每个聚类内各个节点的访问顺序之后,将聚类分配给无人机。

上述聚类的度量没有考虑障碍物的影响。本文对聚类的度量进行了改进。上述度量存在的问题以及改进方法如图4所示。

图4 Sabo的度量存在的问题Fig.4 Problem in Sabo’s measurement

图4中黑色粗线段表示边界或者障碍;x1和x2分别为利用Dijkstra算法求解得到的圆形节点1和节点2到基站的路径长度;x3和x4分别为圆形节点1和节点2到基站的欧式距离,显然两者相近。另外,相对基站的方位夹角β也很小。按照Sabo的度量方法,显然节点1和节点2可以聚成一类。但实际上,从节点1到节点2的路径长度远大于两者之间的欧式距离,若将节点1和节点2聚成一类,无人机在遍历该聚类时,将会行驶很长的路径才能从节点1到达节点2,这将极大增加式(1)的目标函数值,产生较差的结果。

本文对该度量进行了改进,在求解两个聚类Cluu、Cluv之间的距离d(Cluu,Cluv)时,设两个节点Tri和Trj满足Tri∈Cluu,Trj∈Cluv。在计算两个节点i和j的距离时,采用的第一个度量αij为两个节点i和j到基站的路径长度(利用Dijkstra算法所得长度)yi和yj之比:

(6)

yi和yj分别对应x1和x2。设两个节点i和j之间的路径长度为qij,则采用的第二个度量为βij:

(7)

式(7)由余弦定理得到,βij为两个节点相对基站方位的“广义”夹角。在使用该度量时,显然需要满足如下条件:yi、yj和qij可以构成一个三角形。

若3条边满足最短两边之和大于第3边,那么这3边可以构成一个三角形,由于Dijkstra算法所求的距离为两个点之间的最短距离,故易证yi、yj和qij满足该条件,也即可以构成一个三角形。

综上所述,yi和yj的距离度量d(Tri,Trj)为

d(Tri,Trj)=f(αij,βij)

(8)

式中:f(·)表示模糊规则。该规则的具体参数文献[2]已经说明。最后,得到两个聚类的距离d(Cluu,Cluv)为

(9)

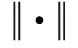
对于处于基站通信范围内的点,无人机先进行覆盖,这样可以较快将通信范围内的点信息传回基站。这些点不需要进行聚类,可直接求解最短路径。无人机在遍历完这些点之后,开始覆盖位于基站通信范围之外的点。在每次无人机覆盖完一个聚类的点之后,需要在通信范围内找到距离无人机返回点最近的点,无人机只需运动到该点即可将信息传回基站。同理,在区域全覆盖的情形下,也可采用该方法处理基站通信范围之内和之外的点。另外,可利用Dijkstra算法求解地图上所有位点之间的最短路径长度。

2.2 区域全覆盖的情形

对于区域全覆盖的情形,此时需要覆盖的位点分布均匀,而且区域中的点比较密集。相比于第2.1节中点较为分散的情形,需要进一步考虑无人机模型的影响。采用第2.1节中的覆盖路径求解方法显然没有对覆盖路径上路径平滑程度、转弯半径等进行考虑(在待覆盖点较为分散时该问题并不突出)。

对于此问题,本文提出一种三阶段的优化方法,即图3中步骤(a)～步骤(c)。针对步骤(a),先利用Boustrophedon法进行单元分解,利用智能优化方法优化单元之间和单元内的覆盖路径,具体步骤采用文献[17]的方法。该文献中求解的路径考虑了上述因素。以下具体介绍步骤(b)基于目标函数提取最优返回次数的可能范围和步骤(c)基于最优返回次数所处范围的返回位点智能优化。

2.2.1 基于目标函数分析提取最优返回次数的可能范围

在研究复杂规划问题时,智能优化方法必须要与问题特征相结合,才能发挥更好的搜索效果。可以利用运筹学方法分析得到问题特征,但利用其对最优解的特征进行严格理论分析时,可能会面临难以求解的情形。因此,本阶段在对问题的目标函数进行分析时,采取的思想方法是抓住影响目标函数的主要因素,忽略不重要的因素,按此方法得到问题特征。此特征虽无法得到严格理论证明,但对搜索最优解仍具有一定的指导意义。

由于选取合适的返回次数将会发挥重要的作用,因此可以基于此分析目标函数,得到最优返回次数可能的范围。

(10)

基于图3中步骤(a)得到的覆盖路径,将单元之间的衔接路径点集视作无效请求点集P,单元内部的覆盖路径点集视作有效请求点集Q,总点集合元素数量为

(11)

(12)

式中:M/K表示无人机一次覆盖的点数。

(13)

综上,现在需要完成以下目标:

(14)

对目标函数求导得到:

(15)

得到最优返回次数:

(16)

2.2.2 基于最优返回次数所处范围的返回位点智能优化

第2.2.1节得到最优返回次数所处范围,该阶段利用此范围先搜索最优返回次数,此后利用遗传算法进一步优化返回位点位置。

步骤 1对由图3中的步骤(a)得到最短的覆盖路径P,对其进行K*等分,设在覆盖路径上的分割点(或者称为返回点)对应的序号集合为X={Xr|r={1,2,…,K*}}。

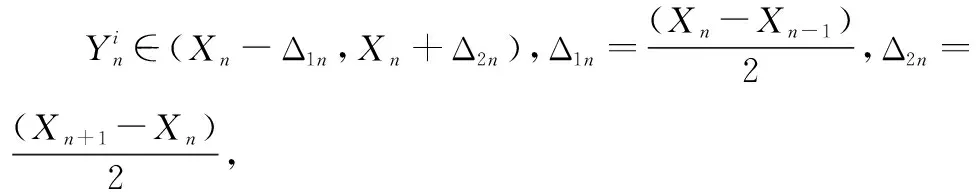
步骤 3采用均匀随机初始化方法初始化每个个体的每个基因位:

(17)

生成Np个个体,组成种群A1。

步骤 4开始进化,利用锦标赛方法[30]从A1中选取两个个体s1和s2。若rand小于交叉概率Pc,则随机选取一段基因位进行交叉:

(18)

式中:h为需要交叉的位置。

步骤 5若rand小于变异概率Pm,对个体s1和s2进行变异,随机选取一个位置m,针对基因位变异,有:

s(m)=(Xm-Δ1m)+rand·(Δ2m+Δ1m)

(19)

步骤 6将上述s1和s2作为子代种群中的成员,重复步骤4和步骤5,生成Np个子代成员。将A1中Np个个体与该Np成员合并,找到目标函数值排在前Np位的个体作为新的子代A1,用于之后的进化。

步骤 7重复步骤4～步骤6,直到输出最优的返回位点,其伪代码如算法1所示。

算法 1 基于遗传算法的返回位点智能优化输入覆盖路径P,最优返回次数K*输出P上最优返回位点集合S 1将P划分成 K*等份, 据此获得每次的覆盖点集合,设X={Xr|r={1,2,…,K*}}2先求初始解:设第i个个体对应的染色体为Yi={Yi1,Yi2,…,YiK*}其中染色体的每一位为Yin∈(Xn-Δ1n,Xn+Δ2n),其中的参数Δ1n=[(Xn-Xn-1)]/2,Δ2n=[(Xn+1-Xn)]/23初始化种群A1←Ø4For i=1:Np Do5For n=1:K* 6 Yin=(Xn-Δ1n)+rand·(Δ2n+Δ1n)7End For8 A1←A1∪Yi9End For10For u=1:Gmax Do11A2←Ø在A1中利用锦标赛算法和目标函数式(1)得到两个个体s1 and s212If rand

2.3 算法时间复杂度分析

对于第2.1节中非区域全覆盖的情形,其算法复杂度已经在文献[2]中进行了分析,本文相对于其算法只增加利用Dijkstra算法求解地图上所有点之间距离这一步骤,该部分的时间复杂度为O(M3),M为环境中自由位点的数量。

本文重点对区域全覆盖的时间复杂度进行了分析,时间复杂度包含图3中步骤(a)～步骤(c)3个阶段的时间复杂度,以下的时间复杂度都是在最差情况下的结果。在步骤(a),使用了Dijkstra算法求解所有环境位点间的路径长度,该部分的时间复杂度为O(M3)。设采用Boustrophedon法单元分解总的时间复杂度为O(M),设得到的单元数量为B。所有单元对应的多边形最大边数为A,则RCPP求解每个单元内覆盖路径的总时间复杂度为O(MA)。设置利用智能算法求解的单元迭代次数为G,单元间优化的时间复杂度为O(GB)。故步骤(a)的时间复杂度为O(M3+M+MA+GB)。

步骤(b)在计算所有点到基站的距离时直接利用步骤(a)的结果,故计算时间复杂度为O(M)。设步骤(c)遍历搜索的次数为F。设步骤(c)进化代数为G2。步骤(c)的时间复杂度为O((G2+F)M),则总体时间复杂度为

f=O(M(2+M2+A+G2+F)+GB)

(20)

3 仿真实验

本文的实验环境为Windows10系统下基于C++的Qt环境,运行内存为16 GB。本文的验证思路为:先验证第2.1节提出的聚类距离度量方法的优越性,此后对第2.2.1节中的重要参数最优返回次数等进行调节和分析。最后,为了验证3阶段优化算法的优越性,将本文算法与前沿算法进行对比。

3.1 非区域全覆盖方法对比

实验采用如图5所示的各种地图。

图5 实验用地图(非区域全覆盖)Fig.5 Maps used in the experiment (non regional full coverage)

图5中,黑色部分表示障碍物,绿色的栅格点集合为待访问的点集合。设无人机的移动速度为1个单位/s。本节验证步骤(a)覆盖规划算法的优越性,两个对比算法为:① 文献[2]中的Sabo的算法;② 结合文献[17]的方法得到覆盖路径,再利用遗传算法求解返回位点。两个算法的对比结果如表1所示。

表1 目标函数平均值Table 1 Mean values of objective functions s

从表1可以看到,本文算法在目标函数值上显然优于所有对比算法,本文算法采取的聚类距离度量考虑了障碍物的影响。利用Dijkstra算法求得两个点之间的路径长度,并以此对目标点聚类,避免相距较远的两个点聚成一类。针对图5(a)的各种算法的规划如图6所示。

图6 规划结果(非区域全覆盖)Fig.6 Planning results (non regional full coverage)

图6中,左下角的蓝色区域为基站的通信范围(通信范围半径设置为3),每次的覆盖路径用不同颜色的曲线表示(为方便观察,省略了无人机往返基站通信范围的路径)。如图6(a)所示,本文算法中蓝色曲线和红色曲线为两段覆盖路径;而图6(b)中Sabo的算法将处于障碍物两侧的一部分点集合聚成了一类,导致一次覆盖的路径过长,降低了目标函数的质量;而图6(c)则没有利用Sabo所分析的问题特征,求解质量较差。

3.2 针对区域全覆盖场景的参数调节

图7 实验用地图(区域性全覆盖)Fig.7 Maps used in the experiment (regional full coverage)

所得结果如表2所示。可以看到,λ值在分别取1、2、3时目标函数值相近且返回次数相近,参数在一定范围内变化所引起的目标函数值变化并不敏感。返回次数不在该范围内时,所得目标函数基本稍微劣于λ值为3对应的情况,而且此时返回次数与λ值为3对应的返回次数相近。经观察,在λ=3的情形下将会取得最优的效果,而且对应的返回次数搜索范围较小,由此可确定参数的取值。

表2 不同λ参数目标函数平均值对比Table 2 Comparison of mean values of objective functions with different λ s

3.3 区域全覆盖对比实验

经调研,近年来有关该问题的算法极少,本文选取的对比算法之一为Sabo的算法[2]。当环境中待访问位点数量较少时,Sabo通过实验验证其算法运行所得结果的目标函数值与最优解相差不超过5%,因此可以将其作为一个有相当竞争力的对比算法。另外,采取的前沿对比算法为:利用文献[17]的方法得到覆盖路径,再利用遗传算法求解返回位点。采用图7所示的4个地图进行实验,对比结果如表3所示。图8为针对图7(b)地图2的各算法规划结果,设无人机的移动速度为1个单位/s。图8蓝色区域为基站的通信范围,本文算法和对比算法均优先覆盖基站通信范围内的目标点集合,即各算法在这部分点对应的目标函数值均相同,故表3中不再考虑这部分位点的目标函数值。图8中,无人机每次的覆盖路径用不同颜色的曲线表示,为方便观察,省略了无人机往返基站通信范围的路径。

表3 目标函数平均值对比Table 3 Comparison of mean values of objective functions s

图8 规划结果(区域全覆盖)Fig.8 Planning results (regional full coverage)

从表3和图8可以看到,Sabo的算法中将所有聚类的位点内规划问题视作旅行商规划问题,随着位点数量增加,使用智能优化方法所得的目标函数值变差,而且经常容易产生转角过大的路径,不利于无人机飞行。

本文算法虽然存在表现上稍差的情形,即所求得的目标函数值稍逊于Sabo算法的结果,但从图8可以看到其覆盖路径显著优化,路径较为平滑。

图8(c)中的算法由于没有关注问题的特征,所以所得无人机往返基站通信范围的次数较多,导致目标函数质量下降。

以上算法消耗的时间如表4所示。

表4 算法运行时间比较Table 4 Comparison of running time consumption of different algorithms s

对比算法和本文算法都需要多次计算目标函数,这些都用到了地图上所有点之间的距离。为减少频繁多次计算目标函数带来的计算压力,需要先利用Dijkstra算法求解地图上所有点之间的路径长度,这一部分计算时间较长。本文算法的其他时间复杂度来自于单元分解、单元间遍历顺序计算,故分解的单元越多,计算时间越长,地图1～地图3单元数量较少,求解时间较短。对比算法的其他计算时间复杂度来源于点集合的层次聚类和类内点集合遍历顺序计算,因此点数量较多时计算时间偏长。

4 结 论

本文分析了间歇式通信下多智能体覆盖问题模型,针对区域非全覆盖和全覆盖两种情形进行了分类讨论,针对非全覆盖的情形提供了一种改进聚类度量的方法,充分考虑了障碍物对于聚类的影响,减少了聚类内遍历路径的长度。针对全覆盖的情形,提出了三阶段智能优化的方法,将覆盖规划问题和间歇式往返基站通信的耦合问题分解求解,每个阶段都抓住了影响目标函数的关键参数,如步骤(a)的覆盖路径长度,步骤(b)的返回次数。在保证较好求解质量的同时,所得的覆盖路径相对于前沿算法取得了显著改进,方便无人机进行飞行。本文重点研究了基于目标函数的问题特征分析方法,确定了关键特征,即最优返回参数的搜索范围。进一步将该方法融合到智能优化的求解之中,先确定关键参数最优返回次数,再进一步优化其他参数的选取,从而更加高效地获得了最优解。