镍基单晶高温合金多组元置换的第一性原理研究
2021-12-02孙浚晞吴雨沁
孙浚晞 杜 婉 肖 斌 吴雨沁 刘 轶
(1.上海大学省部共建高品质特殊钢冶金与制备国家重点实验室,上海 200444; 2.上海大学材料基因组工程研究院,上海 200444)
镍基高温合金广泛用于制造航空飞机发动机以及燃气轮机[1-3]中的燃烧室、涡轮叶片等零部件[4-6]。镍基高温合金的化学成分十分复杂,不同掺杂元素通过不同的强化方式影响高温合金的力学性能。研究合金元素在镍基高温合金γ-Ni和γ′-Ni3Al中的相择优和位点择优占位行为,对分析其在γ-Ni和γ′-Ni3Al中的强化机制至关重要。
目前研究人员主要采用基于密度泛函理论(DFT, density functional theory)的第一性原理方法研究Ni3Al中元素的位点择优,其中倾向于占Ni位的元素较少,大多数元素优先占据Al位。Wu等[7]计算发现,Mo、Re、Ta、W、Ti、Nb、Cr、Y均倾向于占Al位。Zhou等[8]、Yu等[9]和Liu等[10]通过对比原子探针和扫描电镜试验结果以及第一性原理计算结果,验证了掺杂元素的择优占位取向,发现Re、Ru、Cr、Ta倾向占据Al位。通过计算掺杂元素在γ-Ni和γ′-Ni3Al两相中的分配系数,发现Co和Ru倾向于分配到基体相中,而Re和Ta倾向于分配到γ′-Ni3Al相中。Chandran[11]使用第一性原理和蒙特卡洛方法计算得到Ti倾向于占据γ′-Ni3Al相。Shang等[12]利用第一性原理计算得到Ti、Hf、Ta、Cr、Mo、W、Re倾向于占据Al位,而Ru、Co的占位则决定于合金成分。目前,第一性原理研究主要集中于镍基高温合金单位点掺杂的择优占位,有关双位点掺杂的择优占位的研究则较少[13-15],且未见有关三位点掺杂的择优占位的文献报道。
为研究多组元掺杂元素在γ-Ni和γ′-Ni3Al相中的择优占位倾向,在镍基高温合金γ-Ni和γ′-Ni3Al中分别选取了1种和2种三位点掺杂方案:在γ-Ni相中的三位点选取3个最近邻的Ni位点,而在γ′-Ni3Al相中的三位点选取互为最近邻的3个Ni位点或者互为最近邻的2个Ni位点和1个Al位点。本文计算的γ-Ni与γ′-Ni3Al相中单位点掺杂、双位点掺杂、三位点掺杂体系共计1 062种,其中γ′-Ni3Al相的AlNiNi位掺杂体系(XAlYNiZNi@Ni3Al)共594种,γ′-Ni3Al相的NiNiNi位掺杂体系(XNiYNiZNi@Ni3Al)共234种,γ-Ni相中NiNiNi位掺杂体系(XNiYNiZNi@Ni)共234种。利用由第一性原理计算的置换能判断γ-Ni和γ′-Ni3Al相中单位点、双位点、三位点掺杂时的相择优占位及位点择优占位,并对稳定的置换缺陷复合体构型进行讨论。本文发现的稳定的多组元置换缺陷复合体对理解镍基高温合金中多组元合金元素协同强化机制提供了理论基础。
1 计算方法和模型
1.1 计算模型与第一性原理计算方法
分别对镍基单晶高温合金中γ-N与γ′-Ni3Al相的三位点合金元素掺杂进行建模。对γ-Ni(FCC)和γ′-Ni3Al(L12)单胞的晶胞体积、晶格常数和离子位置进行弛豫,弛豫后的γ-Ni和γ′-Ni3Al相的晶格常数分别为0.356 4和0.351 3 nm。利用上述晶格常数建立了γ-Ni和γ′-Ni3Al相的2×2×2超胞模型,共有32个原子,如图1所示。图1中蓝色球为Ni原子,粉色球为Al原子,橙色球为本文选取的Al原子,红色球为本文选取的Ni原子。使用测距线标记互为最近邻的3个掺杂位点。
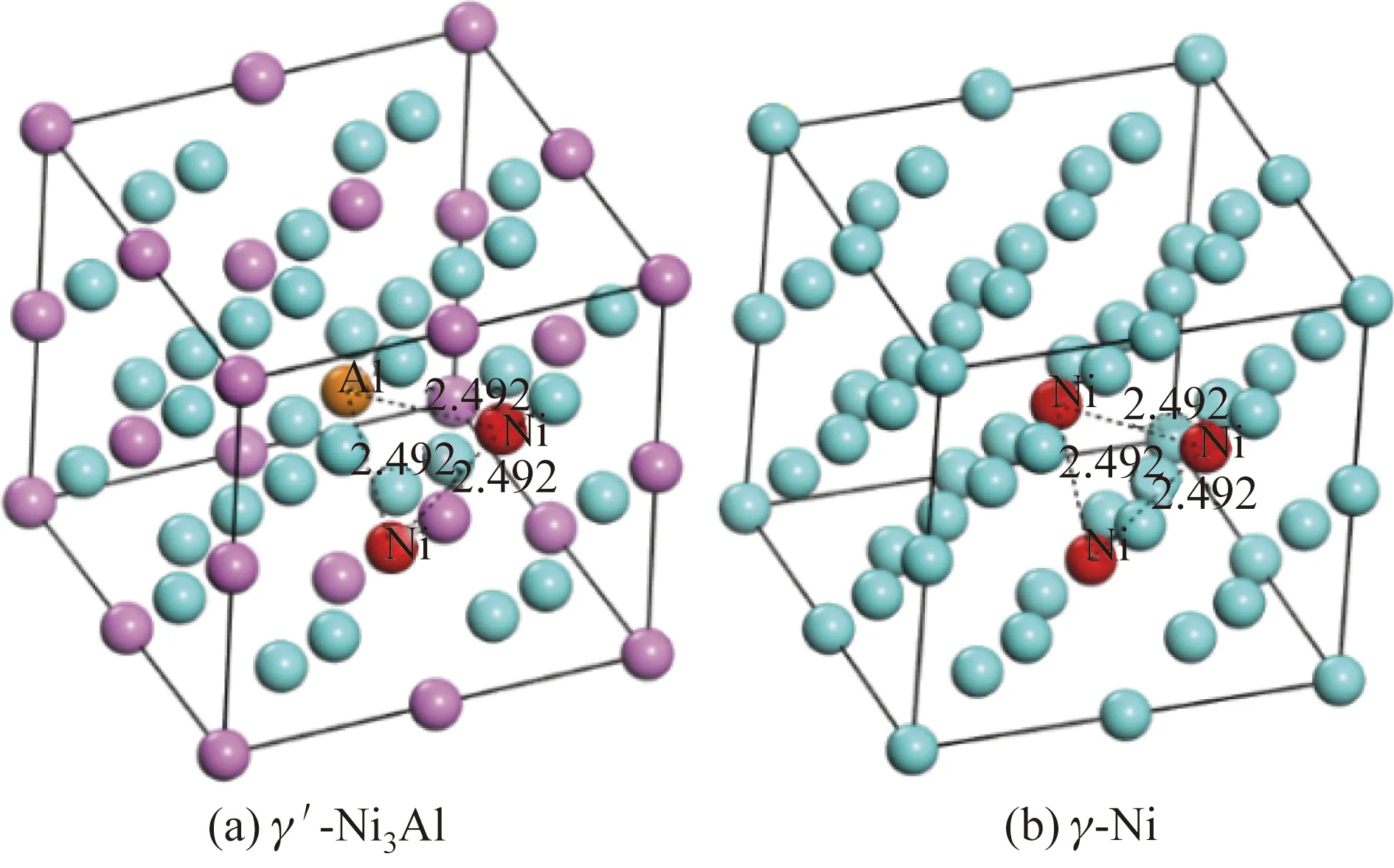
图1 γ′-Ni3Al和γ-Ni超胞的原子结构模型Fig.1 Atomic structure model of γ′-Ni3Al and γ-Ni supercell
γ-Ni相中只有1种不等效位点,而γ′-Ni3Al相中有Al位点与Ni位点2种不等效位点,即Al原子位点与Ni原子位点分别是各自的等效位点。在γ′-Ni3Al和γ-Ni两相中选取3种不等效位点组合:第1种组合是在Ni3Al中选取互为最近邻的AlNiNi 3个掺杂位点(XAlYNiZNi@Ni3Al);第2种组合是在Ni3Al中选取互为最近邻的NiNiNi 3个掺杂位点(XNiYNi-ZNi@Ni3Al);第3种组合是在Ni中选取互为最近邻的NiNiNi 3个掺杂位点(XNiYNiZNi@Ni)。通过文献调研确定了常用的9种掺杂合金元素,即X,Y,Z可为Al、Co、Cr、Hf、Mo、Ni、Ta、Ti、W元素,统计得到γ′-Ni3Al和γ-Ni两相中单位点、双位点、三位点掺杂体系共1 062种。
建立超胞模型后,固定Ni和Ni3Al体系的晶格常数,充分弛豫离子位置,然后进行电子自洽计算得到体系的能量。利用第一性原理计算出1 062种位点掺杂体系的总能量,在计算过程中仅考虑第一近邻(FNN, first nearest neighbor)原子,模型中待掺杂的3个位点互为第一近邻位点。采用VASP软件包[16-19]进行密度泛函理论计算,赝势函数选用投影缀加波(PAW, projected augmented wave)的赝势方法[20-21],交换关联泛函为广义梯度近似的Perdew-Burke-Ernzerhof(PBE)势[22],平面波的截断能为400 eV,布里渊区的k点采用Monkhorst-Pack[23]的撒点方式,模型使用5×5×5的k点网格。电子自洽计算的能量收敛标准为10-5eV,晶体所有原子在固定晶格常数的条件下进行完全弛豫,直至原子的局部力小于0.1 eV/nm[24-25]。
1.2 置换能公式
根据第一性原理,若置换Ni位点,则三位点掺杂的单位点置换能ESS的计算公式为:
ESS=Etot+ENi-Epure-Em1
(1)
置换Al位点,则ESS的计算公式为:
ESS=Etot+EAl-Epure-Em1
(2)
式中:Etot为基于DFT计算得到的三位点掺杂后系统的总能量;Epure为未掺杂合金元素的γ′-Ni3Al或γ-Ni相的能量;EAl为Al原子的能量;ENi为Ni原子的能量;Em1为第1种掺杂合金元素单质体相的每个原子的能量。
置换NiNi位点,则双位点置换能EDS的计算公式为:
EDS=Etot+2ENi-Epure-Em1-Em2
(3)
式中Em2为第2种掺杂合金元素单质体相的每个原子的能量。
置换AlNi位点,则EDS的计算公式为:
EDS=Etot+EAl+ENi-Epure-Em1-Em2
(4)
置换AlNiNi位点,则三位点置换能ETS的计算公式为:
ETS=Etot+EAl+2ENi-Epure-
Em1-Em2-Em3
(5)
式中Em3为第3种掺杂合金元素单质体相的每个原子的能量。
置换NiNiNi位点,则ETS的计算公式为:
ETS=Etot+3ENi-Epure-Em1-Em2-Em3
(6)
2 计算结果与分析
2.1 Al元素的掺杂
2.1.1 单位点掺杂
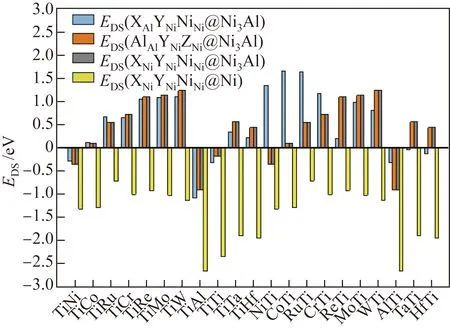
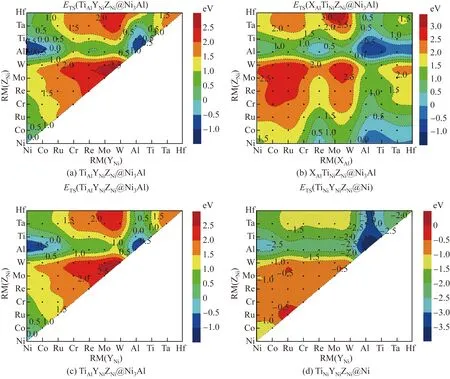
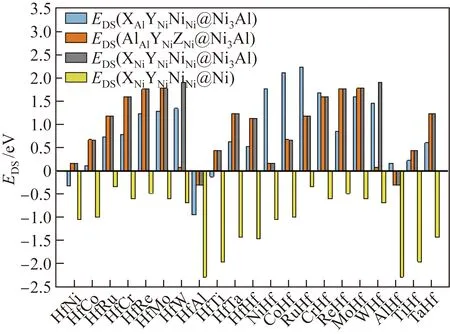
用Al进行单位点掺杂时,γ-Ni与γ′-Ni3Al相中共有3种不等效位点对,即γ′-Ni3Al中的Al位点、γ-Ni中的Ni位点。AlAlNiNiNiNi@Ni3Al的ESS为0 eV,AlAlAlNiNiNi@Ni3Al的ESS为-0.885 eV,AlNiNiNiNiNi@Ni的ESS为-1.511 eV,即ESS(AlNi-NiNiNiNi@Ni) 2.1.2 双位点掺杂 用Al进行双位点掺杂时,共有4种不等效位点对,即XAlYNiNiNi@Ni3Al、AlAlYNiZNi@Ni3Al、XNiYNi-NiNi@Ni3Al、XNiYNiNiNi@Ni。这4种不等效位点对的AlY和XAl双位点掺杂的置换能如图2所示。 图2 γ-Ni与γ′-Ni3Al中4种不等效位点对的AlY和XAl双位点掺杂的置换能(X、Y分别取Ni, Co, Ru, Cr, Re, Mo, W, Al, Ti, Ta、Hf元素)Fig.2 Substitution energies of AlY and XAl dual-site doping for the four non-equivalent dual-site configurations in γ-Ni and γ′-Ni3Al (X and Y standing for one element of Ni, Co, Ru, Cr, Re, Mo, W, Al, Ti, Ta, Hf) 大量Al元素双组元掺杂的双位点置换能为负值,并且分布在4种不等效位点对中。但与前几种掺杂元素相比,在4种不等效位点对中,对于相同的二元掺杂组合,Al在γ-Ni中的EDS(XNi-YNiNiNi@Ni)总是最低。当Al元素与原子半径RM大于0.143 2 nm的元素组成二元掺杂体系时,已为负值的EDS更小。在XNiYNiNiNi@Ni中,当二元掺杂元素组合为AlAl时,EDS最小,即EDS(AlNiAlNiNiNi@Ni)为-2.837 eV。 在γ′-Ni3Al的3种不等效位点对AlAlYNiZNi@Ni3Al、XNiYNiNiNi@Ni3Al和XAlYNiNiNi@Ni3Al中,每个二元组合所对应的EDS(AlAlYNiZNi@Ni3Al)与EDS(XNiYNiNiNi@Ni3Al)几乎相等。对于AlAl-YNiZNi@Ni3Al与XNiYNiNiNi@Ni3Al,如果掺杂元素为Ni、Co、Al、Ta、Ti、Hf,EDS小于0,这些元素可分成两类,一类是原子半径不大于0.125 2 nm的Ni和Co,另一类是原子半径不小于0.143 2 nm的Al、Ta、Ti、Hf;在掺杂元素原子半径介于0.125 2~0.143 2 nm的二元掺杂体系中,没有EDS小于0的体系。 在XAlYNiNiNi@Ni3Al中,当Al置换Al位点(即单位点置换)时,每个二元掺杂组合的EDS(XAlYNiNiNi@Ni3Al)都大于其他3种双组元掺杂的不等效位点对的EDS,表明Al在γ′-Ni3Al中的二元掺杂倾向于占据Ni位点。当Al置换Ni位点时,EDS与掺杂元素原子半径未呈现出线性关系,但总体趋势是原子半径较小的掺杂元素所在的体系能量较高,而原子半径较大的掺杂元素所在的体系能量较低,这表明当Al在XAlYNiNiNi@Ni3Al中置换Ni位点时,若置换Al位的掺杂元素的原子半径较大,则更容易得到稳定结构。 2.1.3 三位点掺杂 用Al元素进行三位点掺杂时,共有4种不等效位点对:AlAlYNiZNi@Ni3Al、XAlAlAlZNi@Ni3Al、AlNiYNiZNi@Ni3Al和AlNiYNiZNi@Ni。这4种不等效位点对的AlYZ和XAlZ三位点掺杂的置换能如图3所示。由图3可以看出,大量Al元素三位点掺杂的置换能为负值。 图3 γ-Ni与γ′-Ni3Al中4种不等效位点对的AlYZ和XAlZ三位点掺杂的置换能Fig.3 Substitution energy of AlYZ or XAlZ triple-site doping for the four non-equivalent triple-site configurations in γ-Ni and γ′-Ni3Al 在AlAlYNiZNi@Ni3Al构型中,当YZ组合为AlAl或者NiAl时,体系能量较低。如果Y与Z均为Al元素,则该体系AlAlAlNiAlNi@Ni3Al实质上是双组元置换体系。如果Y为Ni元素,Z为Al元素,则该体系AlAlNiNiAlNi@Ni3Al实质上是单组元置换体系。当YZ组合为AlAl时,体系能量最低,ETS(AlAlAlNiAlNi@Ni3Al)为-1.476 eV;当YZ的组合为WW时,体系能量最高,ETS(AlAlWNi-WNi@Ni3Al)为2.520 eV。 在XAlAlNiZNi@Ni3Al构型中,当置换Al位点的X元素的原子半径不小于Re时,体系的ETS小于0,AlAlAlNiAlNi@Ni3Al体系的ETS最低,为-1.476 eV。因此,在Al元素的三位点掺杂中,Al置换Ni位点的反位置换可得到最稳定的体系。 在AlNiYNiZNi@Ni3Al构型中,当Y和Z的原子半径介于0.125 2~0.143 2 nm之间时,体系能量均大于0。导致体系ETS小于0的元素可以分成两类,一类是原子半径不大于0.125 2 nm的Ni和Co,另一类是原子半径不小于0.143 2 nm的Al、Ta、Ti、Hf。如果Y和Z置换元素分别为Al和Ni,则体系的ETS最低,为-1.476 eV;当YZ组合为AlAl时,体系的ETS也较低,为-1.390 eV。 在AlNiYNiZNi@Ni构型中,所有体系的能量均为负值,说明在γ-Ni中使用Al元素置换Ni位后可有效稳定体系。当3个Ni位点均被Al原子置换时,体系的ETS最低,为-3.973 eV。 2.2.1 单位点掺杂 当Ti作为掺杂元素进行单位点掺杂时,在γ-Ni与γ′-Ni3Al中共有3种不等效位点,即γ′-Ni3Al中的Al位点、Ni位点以及γ-Ni中的Ni位点。TiAlNiNiNiNi@Ni3Al的ESS为-0.276 eV,AlAl-TiNiNiNi@Ni3Al的ESS为-0.345 eV,TiNiNiNiNiNi@Ni的ESS为-1.314 eV,即ESS(TiNiNiNiNiNi@Ni) 2.2.2 双位点掺杂 用Ti元素进行双位点掺杂时,共有4种不等效位点对:XAlYNiNiNi@Ni3Al、AlAlYNiZNi@Ni3Al、XNiYNiNiNi@Ni3Al、XNiYNiNiNi@Ni。这4种不等效位点对的TiY和XTi双位点掺杂的置换能如图4所示。 图4 γ-Ni与γ′-Ni3Al中4种不等效位点对的TiY和XTi双位点掺杂的置换能Fig.4 Substitution energies of TiY and XTi dual-site doping for the four non-equivalent dual-site configurations in γ-Ni and γ′-Ni3Al 在这4种不等效位点对中,对于相同的二元掺杂组合,Ti在γ-Ni中掺杂后体系的EDS(XNi-YNiNiNi@Ni)总是最低。与Al元素的二元掺杂相同,当Ti元素与原子半径大于0.143 2 nm的元素组成二元掺杂体系时,EDS很小。在XNiYNiNiNi@Ni中,当二元掺杂元素组合为TiAl时,EDS最小,为-2.655 eV。 在γ′-Ni3Al中的2种不等效位点对AlAlYNi-ZNi@Ni3Al、XNiYNiNiNi@Ni3Al中,每个二元组合所对应的EDS(AlAlYNiZNi@Ni3Al)与EDS(XNiYNi-NiNi@Ni3Al)几乎相等。对于AlAlYNiZNi@Ni3Al与XNiYNiNiNi@Ni3Al,只有掺杂元素的组合为TiNi、TiAl和TiTi时,EDS才小于0。除了含有Hf元素的体系外,γ′-Ni3Al中的这2种不等效位点对都呈现出相同的规律,即以Al元素为界,EDS与原子半径之间呈正比关系,随着掺杂元素原子半径的增加,体系EDS逐渐增大。 在XAlYNiNiNi@Ni3Al中,当Ti置换Al位点时,每个TiAlYNiNiNi@Ni3Al的变化趋势与Ni3Al中其余两种不等效位点对的变化趋势相似。在TiCo、TiRu位点对中,Ti更倾向于占据γ′-Ni3Al中的Ni位,而在其他9种位点对中,Ti更倾向于占据Al位点。当Ti置换Ni位点时,原子半径较小的掺杂元素所在的体系能量较高,而原子半径较大的掺杂元素所在的体系能量较低。由此可知,当Al在XAlYNiNiNi@Ni3Al中置换Ni位点时,若置换Al位的掺杂元素的原子半径较大,则获得的体系结构较稳定。 2.2.3 三位点掺杂 用Ti元素进行三位点掺杂时,共有4种不等效位点对:TiAlYNiZNi@Ni3Al、XAlTiNiZNi@Ni3Al、TiNiYNiZNi@Ni3Al、TiNiYNiZNi@Ni。这4种不等效位点对的TiYZ和XTiZ三位点掺杂的置换能如图5所示。 图5 γ-Ni与γ′-Ni3Al中4种不等效位点对的TiYZ和XTiZ三位点掺杂的置换能Fig.5 Substitution energies of TiYZ or XTiZ triple-site doping for the four non-equivalent triple-site configurations in γ-Ni and γ′-Ni3Al 在TiAlYNiZNi@Ni3Al构型中,当YZ组合为AlAl或者NiAl时,体系能量较低。当YZ组合为NiAl时,体系能量最低,ETS(TiAlNiNiAlNi@Ni3Al)为-1.080 eV;当YZ组合为AlAl时,ETS(TiAlAlNi-AlNi@Ni3Al)为-0.531 eV;当YZ组合为WW时,体系能量最高,ETS(AlAlWNiWNi@Ni3Al)为2.676 eV。 在XAlTiNiZNi@Ni3Al构型中,只有当置换Al位点的X元素的原子半径不小于Re的,并且置换Ni位点的Z元素为Ni或者Al时,体系ETS才小于0。AlAlAlNiTiNi@Ni3Al的ETS最低,为-0.901 eV。因此,在Ti元素的三位点掺杂中,Ti倾向于占据Ni3Al中的Ni位点。 在TiNiYNiZNi@Ni3Al构型中,当YZ置换元素为NiAl时,体系能量最低,ETS(TiNiNiNiAlNi@Ni3Al)为-0.852 eV。YZ置换元素组合为AlAl、CoAl、TiAl、RuAl、NiNi、NiTi的6个不等效位点体系的置换能均小于0,这些组合中掺杂元素的原子半径与Ni或者Al元素的较接近。 在TiNiYNiZNi@Ni构型中,所有体系能量均为负值,说明在γ-Ni中用Ti元素置换Ni位可得到稳定结构。当置换组合为TiAlAl时,ETS最小,为-3.809 eV。 2.3.1 单位点掺杂 用Ta进行单位点掺杂时,在γ-Ni与γ′-Ni3Al中共有3种不等效位点,即γ′-Ni3Al中的Al位点、Ni位点以及γ-Ni中的Ni位点。TaAlNiNiNiNi@Ni3Al的ESS为-0.224 eV,AlAlTaNiNiNi@Ni3Al的ESS为0.267 eV,TaNiNiNiNiNi@Ni的ESS为-0.941 eV,即ESS(TaNiNiNiNiNi@Ni) 2.3.2 双位点掺杂 用Ta元素进行双位点掺杂时,共有4种不等效位点对:XAlYNiNiNi@Ni3Al、AlAlYNiZNi@Ni3Al、XNiYNiNiNi@Ni3Al、XNiYNiNiNi@Ni。这4种不等效位点对中TaY和XTa双位点掺杂的置换能如图6所示。 图6 γ-Ni与γ′-Ni3Al中4种不等效位点对的TaY和XTa双位点掺杂的置换能Fig.6 Substitution energies of TaY and XTa dual-site doping for the four non-equivalent dual-site configurations in γ-Ni and γ′-Ni3Al 在4种不等效位点对中,对于相同的二元掺杂组合,Ta在γ-Ni中掺杂后体系的EDS(XNiYNi-NiNi@Ni)总是最低。与Al和Ti元素的双位点掺杂后的相同,当Ta元素与原子半径大于0.143 2 nm的元素组合成二元掺杂体系时,EDS突然变得很小。在XNiYNiNiNi@Ni中,当二元掺杂元素组合为TaAl时,EDS最小,为-2.201 eV。 在γ′-Ni3Al的2种不等效位点对AlAlYNi-ZNi@Ni3Al、XNiYNiNiNi@Ni3Al中,每个二元组合所对应的EDS(AlAlYNiZNi@Ni3Al)与EDS(XNiYNi-NiNi@Ni3Al)的数值相差10-4eV左右。对于AlAl-YNiZNi@Ni3Al与XNiYNiNiNi@Ni3Al,只有双组元掺杂元素的组合为TaAl时,EDS才小于0。除了含Hf元素的体系外,γ′-Ni3Al中2种不等效位点对都呈现出相同的规律:以Al元素为界,EDS与原子半径之间均呈正比关系。 在XAlYNiNiNi@Ni3Al中,当Ta置换Al位点时,每个TaAlYNiNiNi@Ni3Al的变化趋势与Ni3Al中其余2种不等效位点对的变化趋势相似,即以Al元素为界,EDS与原子半径之间均呈正比关系。对比Ni3Al中3种不等效位点对的置换能发现,每个TaAlYNiNiNi@Ni3Al的置换能都小于其余2种不等效位点的置换能,这说明双位点掺杂时Ta元素倾向于占据Ni3Al中的Al位。当Ta置换Ni位点时,EDS与掺杂元素的原子半径未呈线性关系。但根据Ta双位点掺杂体系EDS的大小,可将置换Al位的元素分为两类,一类是原子半径小于0.143 2 nm的元素,这类元素所在的Ta双位点掺杂体系的EDS偏高;另一类是原子半径不小于0.143 2 nm的元素,这类元素所在的Ta双位点掺杂体系的EDS偏低。由此可知,当Ta在XAl-YNiNiNi@Ni3Al中置换Ni位点时,若置换Al位的掺杂元素的原子半径较大,则更容易得到稳定结构体系。 2.3.3 三位点掺杂 用Ta元素进行三位点掺杂时,共有4种不等效位点对:TaAlYNiZNi@Ni3Al、XAlTaNiZNi@Ni3Al、TaNiYNiZNi@Ni3Al、TaNiYNiZNi@Ni。这4种不等效位点对的TaYZ和XTaZ三位点掺杂的置换能如图7所示。 图7 γ-Ni与γ′-Ni3Al中4种不等效位点对的TaYZ和XTaZ三位点掺杂的置换能Fig.7 Substitution energies of TaYZ or XTaZ triple-site doping for the four non-equivalent triple-site configurations in γ-Ni and γ′-Ni3Al 在TaAlYNiZNi@Ni3Al构型中,TaNiNi、TaNiAl、TaNiTi、TaCoAl、TaAlTi这5个体系的置换能小于0,其中置换Ni位点的元素至少有1个为Al或Ni元素。与Ti元素的三位点掺杂相似,当YZ组合为NiAl时,体系能量最低,为-0.857 eV;当YZ组合为WW时,体系能量最高,为3.178 eV。 在XAlTaNiZNi@Ni3Al构型中,置换能小于0的三位点掺杂体系只有1种,即AlAlAlNiTaNi@Ni3Al,其ETS最低,为-0.143 eV。因此,三位点掺杂时Ta元素倾向于占据Ni3Al中的Ni位点。 在TaNiYNiZNi@Ni3Al构型中,置换能小于0的体系没有明显的规律性,只出现了2个不等效位点体系的置换能小于0的三位点掺杂体系, 分别为Ta-Al-Al、Ta-Ni-Al。如果YZ置换元素为NiAl,体系能量最低,为-0.143 eV。 在TaNiYNiZNi@Ni构型中,除了TaRuMo、TaMoMo、TaRuRu三位点掺杂体系外,其余体系的能量全部为负值。当置换组合为TaAlAl时,Ta的三位点掺杂体系的ETS最小,为-3.281 eV。 2.4.1 单位点掺杂 用Hf元素进行单位点掺杂时,在γ-Ni与γ′-Ni3Al中共有3种不等效位点,即γ′-Ni3Al中的Al位点、Ni位点以及γ-Ni中的Ni位点。HfAl-NiNiNiNi@Ni3Al的ESS为-0.315 eV,AlAlHfNiNiNi@Ni3Al的ESS为0.174 eV,HfNiNiNiNiNi@Ni的ESS为-1.041 eV,即ESS(HfNi-NiNiNiNi@Ni) 2.4.2 双位点掺杂 用Hf元素进行双位点掺杂时,共有4种不等效位点对:XAlYNiNiNi@Ni3Al、AlAlYNiZNi@Ni3Al、XNiYNiNiNi@Ni3Al、XNiYNiNiNi@Ni。这4种不等效位点对的HfY和XHf双位点掺杂的置换能如图8所示。 图8 γ-Ni与γ′-Ni3Al中4种不等效位点对的HfY和XHf双位点掺杂的置换能Fig.8 Substitution energies of HfY and XHf Dual-site doping for the four non-equivalent dual-site configurations in γ-Ni and γ′-Ni3Al 在4种不等效位点对中,对于相同的二元掺杂组合,Hf在γ-Ni中掺杂后体系的EDS(XNiYNi-NiNi@Ni)总是最低。与Al、Ti、Ta元素的二元掺杂相同,当Hf元素与原子半径大于0.143 2 nm的元素组合成二元掺杂体系时,EDS突然变得很小。在XNiYNiNiNi@Ni中,当二元掺杂元素组合为HfAl时,EDS最小,为-2.270 eV。 在γ′-Ni3Al的2种不等效位点对AlAlYNiZNi@Ni3Al、XNiYNiNiNi@Ni3Al中,除HfW组合外,每个二元组合所对应的EDS(AlAlYNiZNi@Ni3Al)与EDS(XNiYNiNiNi@Ni3Al)相差10-4eV左右。EDS(AlAl-WNiHfNi@Ni3Al)为0.095 eV,而EDS(NiNiWNiHfNi@Ni3Al)为1.916 eV,二者相差较大。对于AlAl-YNiZNi@Ni3Al和XNiYNiNiNi@Ni3Al,只有双组元掺杂元素的组合为HfAl时,EDS才小于0。除了HfW与HfHf这两种二元掺杂体系外,γ′-Ni3Al中的2种不等效位点对的置换能都呈现出相同的规律,即以Al元素为界,EDS与原子半径之间呈正比关系。 在XAlYNiNiNi@Ni3Al中,当Hf置换Al位点时,每个HfAlYNiNiNi@Ni3Al的变化趋势与Ni3Al中其余2种不等效位点对的变化趋势相似,即以Al元素为界,EDS与原子半径之间呈正比关系。对比Ni3Al中的3种不等效位点对的置换能后发现,每个HfAlYNiNiNi@Ni3Al的置换能都小于其余2种不等效位点对的置换能,这说明双位点掺杂Hf元素倾向于占据Ni3Al中的Al位。当Ta置换Ni位点时,EDS与掺杂元素原子半径之间未呈现线性关系,但是当置换元素的原子半径大于等于Al的原子半径时,置换能突然降低。按照EDS大小,可将置换Al位元素分为两类,一类是原子半径小于0.143 2 nm的元素,这类元素所在的Hf双位点掺杂体系的EDS偏高;另一类是原子半径不小于0.143 2 nm的元素,这类元素所在的Hf双位点掺杂体系的EDS偏低。由此可知,当Hf在XAlYNiNiNi@Ni3Al中置换Ni位点时,若置换Al位的掺杂元素的原子半径较大,则体系结构较稳定。 2.4.3 三位点掺杂 用Hf元素进行三位点掺杂时,共有4种不等效位点对:HfAlYNiZNi@Ni3Al、XAlHfNiZNi@Ni3Al、HfNiYNiZNi@Ni3Al、HfNiYNiZNi@Ni。这4种不等效位点对的HfYZ和XHfZ三位点掺杂的置换能如图9所示。 图9 γ-Ni与γ′-Ni3Al中4种不等效位点对的HfYZ和XHfZ三位点掺杂的置换能Fig.9 Substitution energies of HfYZ and XHfZ triple-site doping for the four non-equivalent triple-site configurations in γ-Ni and γ′-Ni3Al HfAlYNiZNi@Ni3Al构型中有6个置换能小于0的掺杂体系,分别为HfNiNi、HfNiAl、HfNiTi、HfCoAl、HfAlTi、HfAlAl。在这6个体系中,置换Ni位点的元素至少有1个为Al或者Ni。当YZ组合为AlAl时,体系能量最低,为-1.175 eV;当YZ组合为WW时,体系能量最高,为3.166 eV。 XAlHfNiZNi@Ni3Al构型中只有1个置换能小于0的三位点掺杂体系,即AlAlAlNiHfNi@Ni3Al,其ETS为-0.292 eV。因此,三位点掺杂时Hf元素倾向于占据Ni3Al中的Al位点。 HfNiYNiZNi@Ni3Al构型中置换能小于0的体系没有明显规律性,只有2个不等效位点体系的置换能小于0,XYZ组合分别为HfAlAl、HfNiAl。如果YZ置换元素为NiAl,体系能量最低,为-0.292 eV。 HfNiYNiZNi@Ni构型中大部分体系能量为负值。只有当三元掺杂元素组合XYZ为ReRuHf、RuRuHf、RuMoHf时,ETS才为正值。当置换组合为HfAlAl时,Hf的三位点掺杂体系的ETS最小,为-3.329 eV。 (1)用9种合金元素在γ-Ni和γ′-Ni3Al相中进行单位点掺杂时,所有元素均倾向于占据γ-Ni相,γ′-Ni3Al相中Ni、Co、Cr、Al、Ti元素倾向于占据Ni位,Mo、W、Ta、Hf元素倾向于占据Al位。 (2)用9种合金元素在γ-Ni和γ′-Ni3Al相中进行双位点掺杂时,所有体系都显示出易分布于γ-Ni相的趋势。当X为Ni、Co、Cr、Al时,XY双位点掺杂倾向于占据γ′-Ni3Al相中的Ni位;当X为Mo、W、Ta、Hf时,XY双位点掺杂倾向于占据γ′-Ni3Al相中的Al位;当X为Ti时,出现了双位点掺杂的协同效应,若Y为Ni、Co、Ru,XY双位点掺杂倾向于占据γ′-Ni3Al相中的Ni位,而若Y为Cr、Re、Mo、W、Al、Ti、Ta、Hf,XY双位点掺杂倾向于占据γ'-Ni3Al相中的Al位。 (3)用9种合金元素在γ-Ni和γ′-Ni3Al相中进行三位点掺杂时,所有体系都显示出易分布于γ-Ni相的趋势。当X为Ni、Co、Cr、Al时,XYZ三位点掺杂倾向于占据γ′-Ni3Al中Ni位;当X为W、Ta、Hf时,XYZ三位点掺杂倾向于占据γ′-Ni3Al中的Al位;当X为Mo、Ti时,出现了三位点掺杂的协同效应,若Y为Ni、Co、Ru,XYZ三位点掺杂倾向于占据γ′-Ni3Al中的Ni位,而若Y为Cr、Re、Mo、W、Al、Ti、Ta、Hf,XYZ三位点掺杂倾向于占据γ′-Ni3Al中的Al位。 (4)在γ′-Ni3Al相中进行位点掺杂时,位点择优与掺杂元素的原子半径密切相关。掺杂元素的原子半径越小,掺杂元素原子越倾向于占据Ni位。掺杂元素的原子半径越大,掺杂元素原子越倾向于占据Al位。在双位点掺杂与三位点掺杂体系中,元素间的协同作用也与掺杂元素的原子半径密切相关。 (5)Al、Ti、Ta和Hf替代γ-Ni相中的Ni位是能量稳定的缺陷构型,还能稳定其他元素在其最近邻位点的置换,且AlNi、TiNi、TaNi~HfNi的稳定效果依次降低,其中反位AlNi是最稳定的缺陷。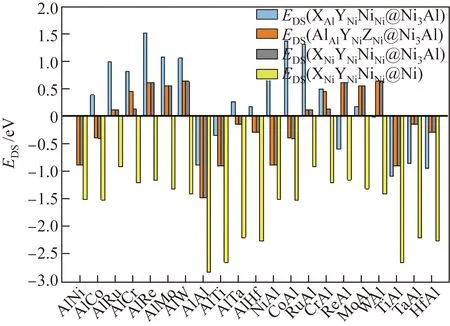

2.2 Ti元素的掺杂
2.3 Ta元素的掺杂


2.4 Hf元素的掺杂

3 结论
