基于PDW多特征融合的辐射源信号分选方法

罗佳奕, 李煊鹏,*, 李江浩, 薛启凡, 杨 凤, 张为公

(1. 东南大学仪器科学与工程学院, 江苏 南京 211189; 2. 中国航天科工集团8511研究所, 江苏 南京 211100)

0 引 言

辐射源信号分选是电子侦察的重要环节,是电磁目标识别和定位的前提保障。通过分选,对接收机获取到的辐射源信号进行特征提取及去交错处理,将混叠的辐射源信号进行区分,进而实现辐射源识别和威胁评估等目的,在现代战争中获取电磁对抗优势。

辐射源分选过程中使用到的主要参数可分为时域、空域和参数域。时域参数主要指脉冲到达时间(time of arrival, TOA);空域参数主要指脉冲到达角(direction of arrival, DOA);参数域参数包括脉冲频率(radio frequency, RF)、脉冲幅值(pulse amplitude, PA)、脉冲相位(pulse phase, PH)、脉冲脉宽(pulse width, PW)等,这些参数构成辐射源脉冲信号描述字(pulse description word, PDW)[1]。现有方法大多依赖时域参数,而忽略其他参数,易使分选结果的准确性不高。

按照分选过程使用数据参数的不同,当前国内外辐射源分选方法主要有以下两大类:基于脉冲重复间隔(pulse repetition interval, PRI)的方法和多参数特征融合方法。

基于辐射源PRI的方法具有物理意义明确、设备配置简便等特点,是过去辐射源信号主分选流程的核心关键技术之一,在辐射源侦察中得到广泛应用。其本质是使用统计学方法,以时域参数TOA为基础计算PRI。常见的PRI分选方法有基于直方图统计的方法和PRI变换法。直方图统计方法对辐射源脉冲序列中各个脉冲TOA的相互差值进行累积计数,构造全差直方图,设定判决门限以检测可能的PRI值。常见的方法如扩展关联法[2]、累计差值直方图法(cumulative difference histogram, CDIF)[3]、序列差值直方图法(sequential difference histogram, SDIF)[4]、PRI变换法等[5]。PRI变换法克服了传统直方图统计法的子谐波问题,具有较好的抗抖动性能[6]。然而,上述方法分选结果的准确性受到脉冲丢失和干扰噪声影响极大。直方图法不适用于重频率抖动信号,且同样受噪声影响较大;PRI变换法在脉冲数据点较多时性能较差。因此,传统PRI分选法只使用时域参数难以适应愈发复杂的战场情况。

基于多参数融合的方法主要包括聚类分选方法和神经网络分选方法。聚类分选方法将多参数组成的无标注样本按照相似性度量进行分组,很适合解决缺乏先验信息的辐射源信号分选问题[7]。对于本研究中的PDW辐射源信号数据,可选用的参数包括TOA、RF、PA、PH、PW等。相似性度量则可以用各种距离公式来衡量,如欧氏距离[8]、汉明距离[9]、马氏距离[10-11]、曼哈顿距离[12-13]等,可灵活运用各种不同的衡量标准以适配数据的实际意义。常见的聚类方法有K-均值算法[14]、空间密度聚类算法(density-based spatial clustering of applications with noise, DBSCAN)[15-16]、排序点结构算法(ordering points to identify clustering structure, OPTICS)[17]、凝聚层次聚类(agglomerative nesting, AGNES)[18]等。然而,常见的聚类方法由于数据信息使用不全或模型自身缺陷,尽管分选精度最高能达到90%左右,但所用数据混叠程度较小。

基于神经网络的分选方法对识别辐射源信号的调制方式也有良好的效果,主要思想为利用不同调制信号的时频差异,将辐射源信号分选问题转化为图像识别问题[19-20]。常见方法有基于长短期记忆(long short-term memory, LSTM)网络的方法[21]、基于卷积神经网络(convolutional neural network, CNN)的方法[22]、基于深度残差网络(deep residual neural network, DRNN)的方法[23]等。然而,基于神经网络的方法需要大量训练样本和标注,耗时较长且可解释性不强,目前仍然不是可以系统化使用的首选方法。

综上所述,基于多参数融合的方法显著降低了对数据的依赖性,相比PRI方法适应性更强,更适合信号点较多的数据集。本文在聚类方法的基础上提出多参数融合的两级分选框架。针对传统聚类方法难以处理混叠信号的问题,提出了时空密度聚类模型以降低时频域脉冲信号的混叠程度,作为第一级分选;针对单一分选方法精度不高的问题,利用信号幅值连续性,使用三维交并比(intersection-over-union, IoU)作为第二级分选,进一步提升总分选精度。

1 基于时空密度聚类和三维IoU的PDW信号分选方法

本研究使用全向干涉仪采集的PDW数据,具有时域、空域、参数域等多个维度的信息,各维度信息在参数空间严重混叠交错。此类数据存在大量噪声干扰,且存在大量脉冲丢失的情况,因此使用传统的PRI分选方法效果较差、精度较低[24]。

本研究提出一种多特征融合的层级分选方法:第一级为时空密度聚类,第二级为三维IoU,两级分选级联输出最终分选结果,算法流程如图1所示。

1.1 时空密度聚类

基于密度的聚类方法将数据集看作若干个高密度簇的集合,并将低密度区域分割,对密集数据点分选效果较好。DBSCAN算法是一种基于密度的常用算法,其核心思想是定义样本邻域、样本间距离及邻域参数,通过样本密度来衡量样本间的可连接性[25]。若某一区域的样本数据点密度大于设定的样本密度分布阈值,则将此样本数据归到此类分选样本集合中,否则,对此样本数据点重新生成新的聚类样本中心点,重新进行样本密度与阈值判断,直到遍历所有的样本数据集合,并生成聚类簇。

DBSCAN算法在一般几何规则分布的数据上表现效果佳[26],但在各维度间数据分布显著离散、或某些数据具有特殊意义时,空间密度聚类效果存疑[27]。

针对PDW信号数据这类具备时间维度,且信号点在时间维度上的密度显著大于其他空间维度的数据,应将时间维度纳入算法以提升效果[28]。因此,本研究在DBSCAN的基础上,将空间密度聚类在时域上进行拓展,构建图2所示的柱体模型时空密度聚类方法(spatial-temporal density-based spatial clustering of applications with noise, ST-DBSCAN),并有如下定义。

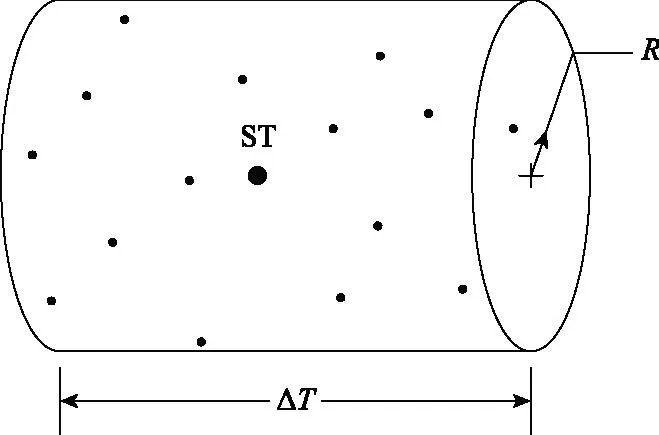
图2 对象的时空邻域柱体模型Fig.2 Spatial-temporal neighborhood of the object

时空实体:在时空多维空间内,选取一个核心点ST,称为时空实体。

时空邻域ε:时空实体ST的时空邻域ε定义为以R为底面半径,ΔT为高的圆柱体,如图2所示。

最低点数Pmin:时空邻域ε内手动设置的一个阈值,表示该邻域内应被包含点的最低数量。

核心对象p:对于给定的时空邻域ε、Pmin,若对象p的ε邻域包含的其他对象点个数Nε(p)满足下式,则点p为核心对象:

Nε(p)≥Pmin

(1)

直接密度可达:对于给定点p和q,若p在q的时空邻域ε内,则称对象p从对象q直接密度可达。

密度可达:对于给定的对象点集合D,若存在一个对象链P1,P2,…,Pn,P1=q,Pn=p,且对Pi∈D,(1≤i≤n),Pi+1从Pi关于ε和Pmin直接密度可达,则称对象p从对象q关于ε和Pmin密度可达。即密度可达由一系列直接密度可达传递得到。TOA-RF-PW三维空间内多个时空实体之间的关系如图3所示,密度可达用单箭头表示。

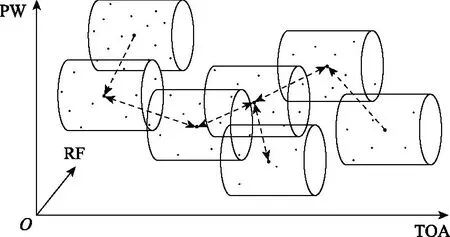
图3 三维ST-DBSCAN示意图Fig.3 Three-dimensional schematic diagram of ST-DBSCAN

密度相连:若对象点集合D中存在一个对象点o,使得对象p和对象q从o关于ε和Pmin密度可达,那么对象p和对象q关于ε和Pmin密度相连。如图3所示,密度相连用双箭头表示。

边界点:若对象点p不是核心对象,而是从某一核心对象q密度可达的对象,则称p为边界点。

噪声点:若对象点p不是核心对象,也不是任何核心对象的密度可达对象,则称p为噪声点。

使用ST-DBSCAN找到密度相连对象的最大集合,并以此为依据进行聚类,实现一级分选。具体分选流程如图4所示。

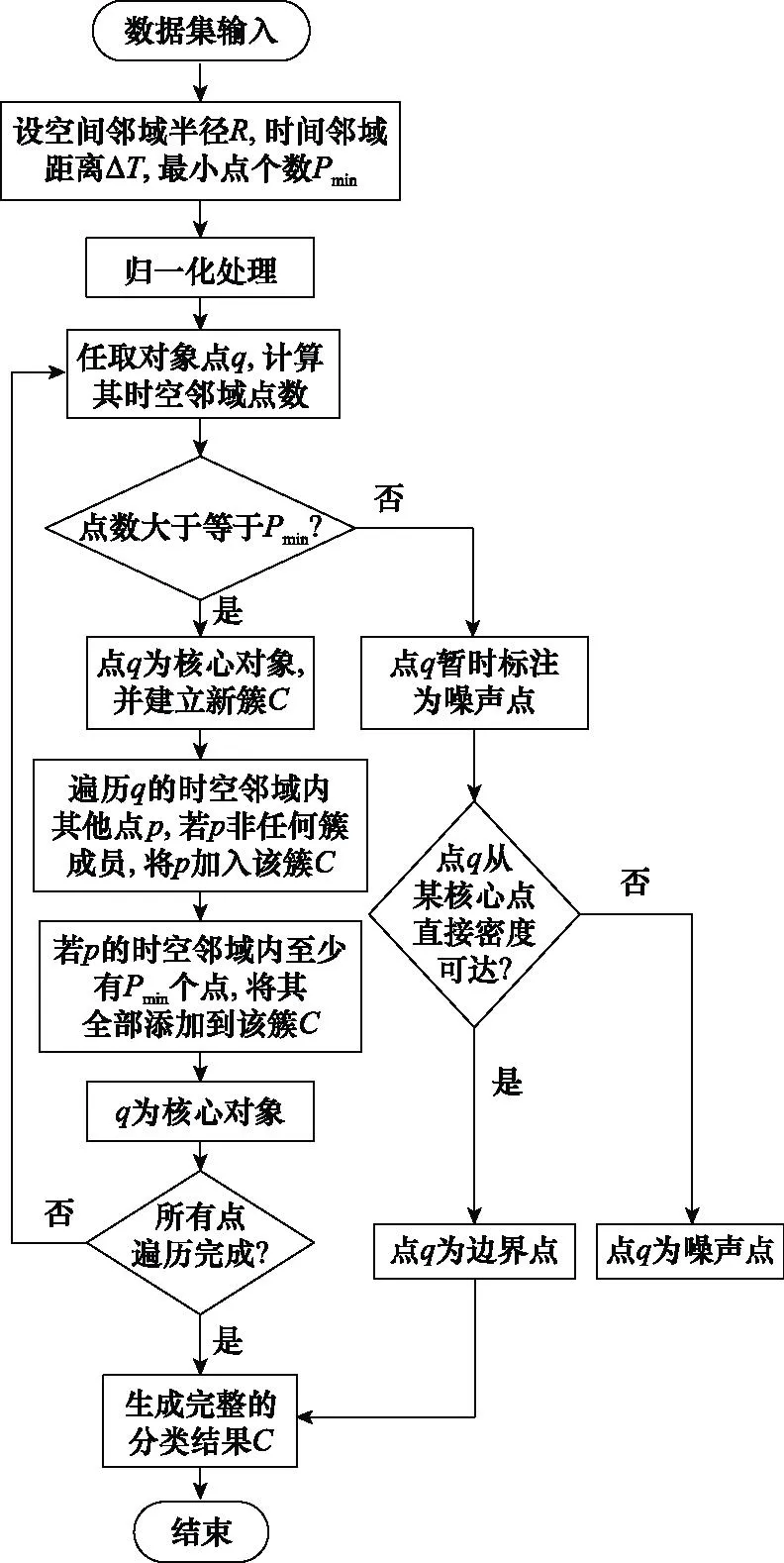
图4 ST-DBSCAN流程图Fig.4 Flow chart for ST-DBSCAN

与空间密度聚类思路相似,为了更好地适配柱体时空模型,应先根据实际情况人工设置时空邻域ε和Pmin参数,通常可直接设置区域半径来实现;为了提升柱体时空模型的效果,RF和PW两维度数据分布应较为均匀,因此需要进行归一化操作;之后,算法遍历检查每个点,从任一核心点出发,不断向密度可达的时空邻域ε扩张,得到一个包含核心点和边界点的最大化区域,视为一个聚类簇,且该簇内任意两点至少是密度相连的。针对所有核心点的统计均完成后,仍未聚类到任何一个簇中的对象将被认为是噪声并删去[29]。

通过上述时空密度聚类方法,可以输出一级分选结果C1,作为二级分选的输入做进一步优化。

1.2 三维IoU算法

IoU是目标检测中一种常见的用来衡量预测值和真实值之间关系的指标,定义为两个矩形交集与并集的比值,取值在[0,1]之间[30]。当IoU=0时,两对象完全无交集,表明其预测结果完全错误;当IoU=1时,两对象完全重合,表明其预测结果完全正确。通过手工设定IoU阈值可以调整分选结果。

一个简易的交并比包含A,B两块区域,定义如下:

(2)

属于同一辐射源的PDW信号在PA维度具备一定的包络特征,且TOA维度上信号点集中;在辐射源非变频调制时,属于不同辐射源的PDW信号在RF维度区分度显著。因此,本研究在TOA-RF-PA三维空间内计算各PDW信号间的IoU。如图5所示,点P1～P5三维邻域的IoU大于阈值,因此属同一点簇;而P6与P1～P5的IoU为0,因此不属于同一点簇。

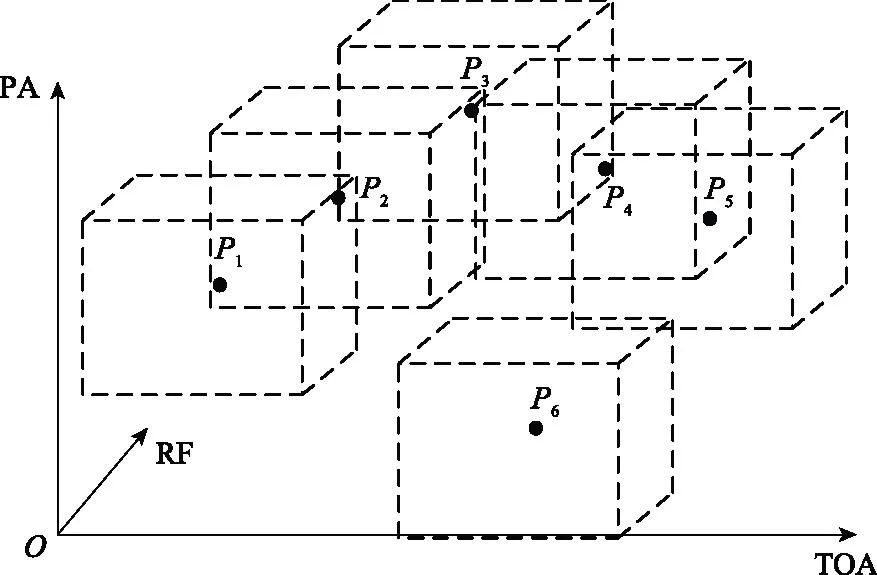
图5 TOA-PA-RF三维空间中的IoUFig.5 IoU in TOA-PA-RF three-dimensional space

在一级分选获取的每一个C1上使用三维IoU分选法,最终获取C2个聚类。

1.3 两级分选级联

综上所述,一级时空密度聚类方法接受原始PDW数据,使用TOA、RF、PW 3类参数输出一级分选结果,将原始数据集分成C1个聚类;二级IoU方法接收一级结果,针对C1中每一类使用TOA、RF、PA 3类参数再次分选,共获得C2个聚类。将二者级联,以输出更优质的分选结果。

“用不着了，我准备明天去自首。”范坚强淡淡地说，“后事已经安排好了，公司的财产已转到你名下，明天开始，你就是一风公司的总经理。我这样做，不是要你原谅我什么，这只是我对你们母子的一点补偿。”

2 实验与结果分析

2.1 仿真数据实验

本研究首先使用仿真模拟数据来验证方法的有效性。根据辐射源连续频率调制方法中的正弦非线性调频获取仿真辐射源信号,此类调频可以产生更高的传输平均功率,较为常用[31]。

如图6所示,仿真数据的具体生成方法如下:先确定组成目标PDW信号集的各簇、各参数取值范围,再对每一簇的频率和幅值分别做正弦型调制,并添加微小扰动以模拟真实情况下的数据误差。生成数据的流程如图6所示。

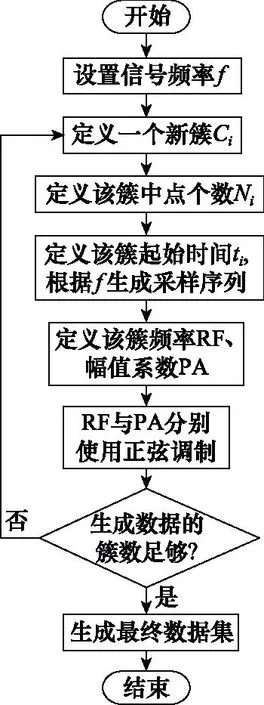
图6 仿真PDW数据生成流程Fig.6 Simulated generation process of PDW data

生成的数据集如图7和图8所示,仿真数据共包含近2 000个数据点,TOA设定在0～1 s,频率分布在0～60 Hz之间,PA绝对值不超过3 dB。

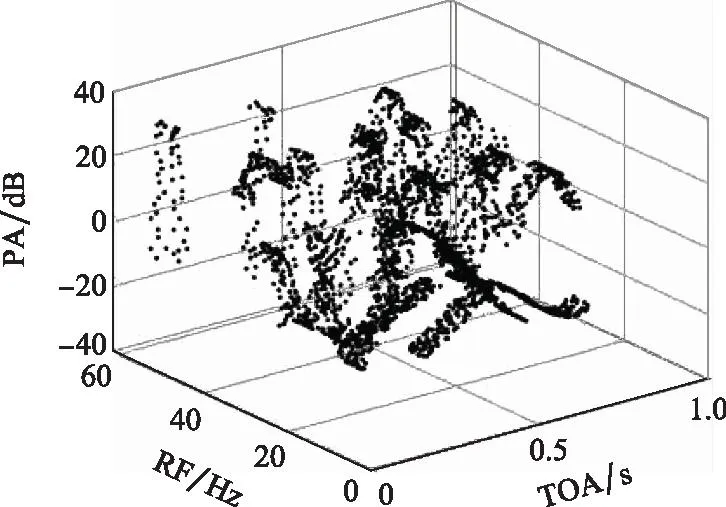
图7 仿真PDW原始数据三维分布Fig.7 Three-dimensional distribution of simulated PDW signals raw data

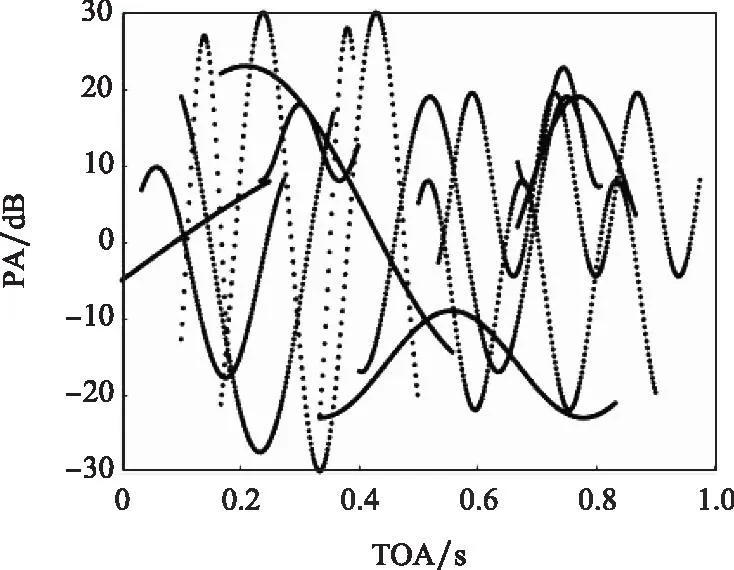
图8 仿真PDW原始数据二维分布Fig.8 Two-dimensional distribution of simulated PDW signals raw data

使用上述时空密度聚类对该仿真数据及进行两级分选,所得结果如图9所示,使用二维图像中的包络线特征做分选结果可视化,其中不同颜色点分别表示分选出的不同类辐射源信号簇。

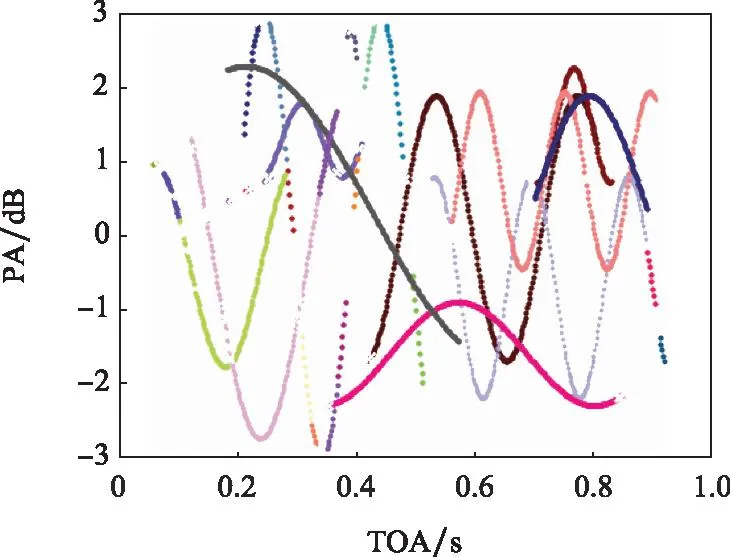
图9 仿真PDW数据分选结果Fig.9 Sorting results of simulated PDW data

与其他同类聚类方法相比,本研究在分选检出率和准确率上都有较大优势,如表1所示。由于K-均值聚类等方法需要提前指定聚类数目,难以满足本研究要求,因此不参与比较。

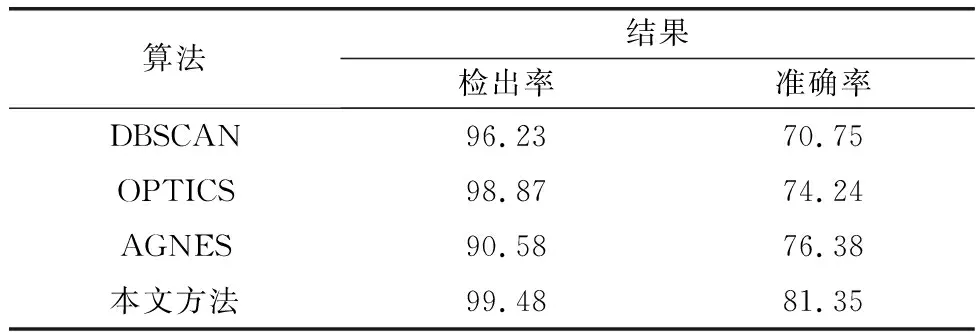
表1 仿真数据实验结果Table 1 Experimental results of simulated data %

2.2 实际数据实验

现代电磁环境下的辐射源信号错综复杂,且考虑到数据安全,常人为添加调制。接收机获取辐射源信号后,可采用数字瞬时测频(digital instantaneous frequency measurement, DIFM)或快速傅里叶变换(fast Fourier transform, FFT)等方法获取PDW信号的频率等参数,并经过变频和模拟变换后,通过模数转换器件量化采样得到幅值等参数[32-33]。

本文使用全向干涉仪实际采集得到的PDW数据为例进行实验。真实数据共有3 000个数据点,包含TOA、RF、PW、PA 4个维度的参数信息,如图10和图11所示,PDW信号在各个参数维度下尺度相差较大,TOA范围为0～64 ms, RF范围在502 MHz左右, PA范围为0～40 dB。

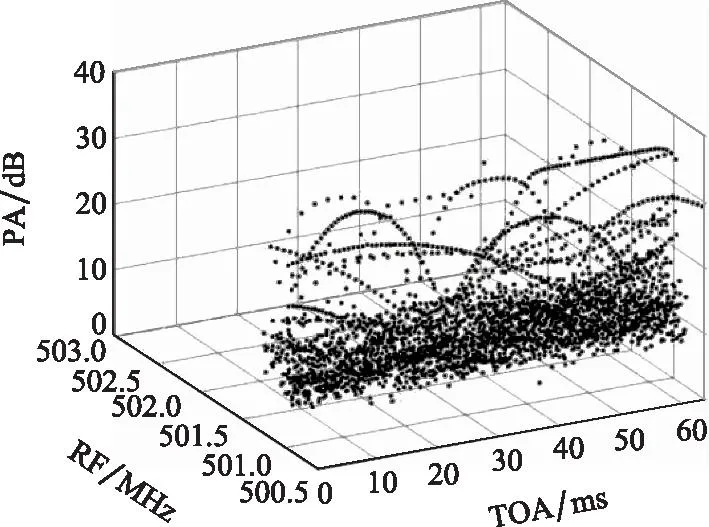
图10 真实PDW原始数据三维分布Fig.10 Three-dimensional distribution of real PDW signals raw data

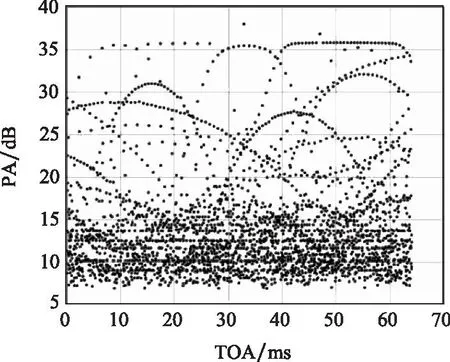
图11 真实PDW原始数据二维分布Fig.11 Two-dimensional distribution of real PDW signals raw data

使用上述时空密度聚类对该仿真数据集进行两级分选,所得结果如图12和图13所示,分别使用三维、二维图像中的包络线特征做分选结果可视化,其中不同颜色点分别表示不同的辐射源信号簇。

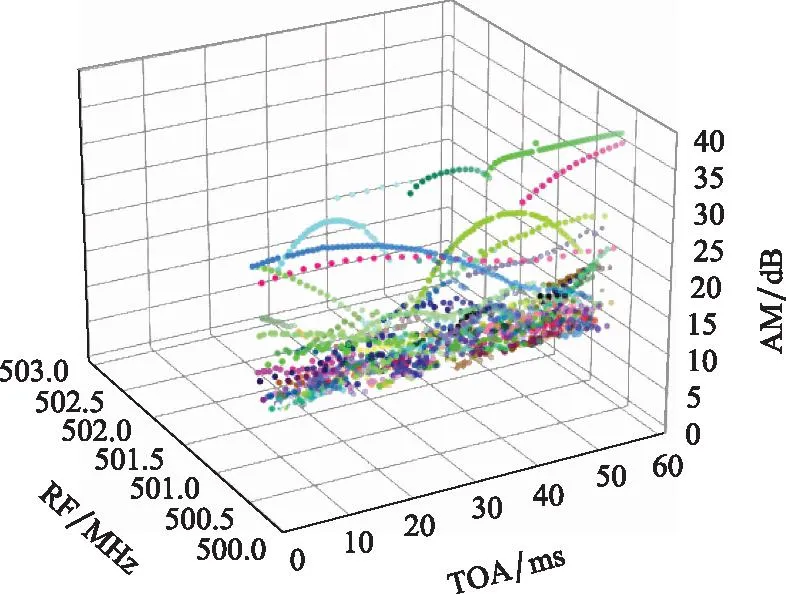
图12 真实PDW数据三维分选结果Fig.12 Three-dimensional sorting results of real PDW data

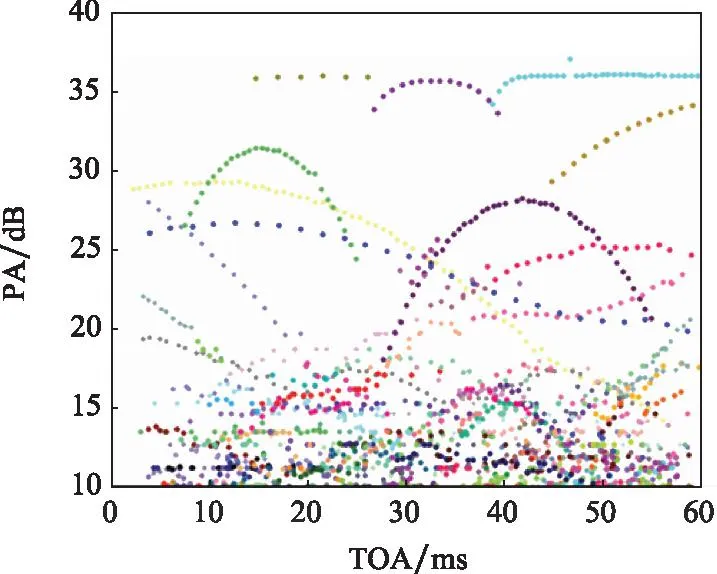
图13 真实PDW数据二维分选结果Fig.13 Two-dimensional sorting results of real PDW data

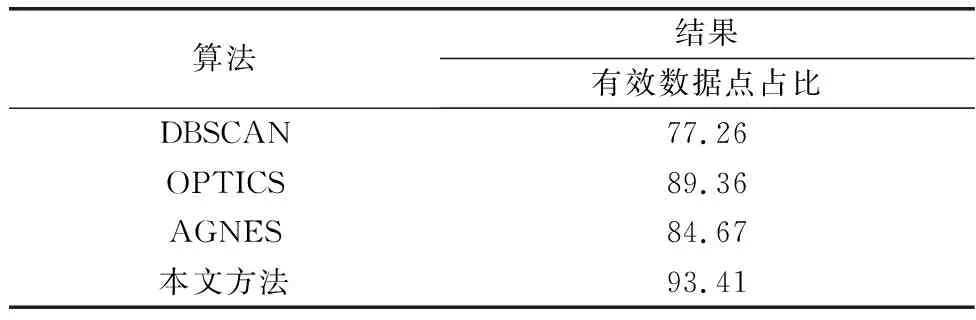
表2 实际数据实验结果Table 2 Experimental results of real data %

被分选后属于同一信号源的簇在TOA-PA空间内呈现明显的正弦包络特征,符合常见的辐射源幅值正弦调制方式[34]。

3 讨 论

本研究分别使用仿真数据和实际数据对多参数融合的辐射源信号分选算法做出检验,均取得可以量化的成果,体现出相比其他聚类分选方法的优越性。

本实验的结果仍可从以下角度进一步提升。

3.1 空间域的标准化尺度不统一

如图14所示,本研究使用的PDW信号数据在频率和脉宽上的分布不统一:在相同的标准化范围条件下,属于同一辐射源的PDW信号点在RF-PW空间内成椭圆分布。其中,横坐标轴为PDW信号点RF,纵坐标轴为PDW信号点PW,使用脉冲的下降沿和上升沿时间之差计算,长短轴差距极大,这导致柱体时空模型中仅使用单一半径R作为空间邻域半径的判定方法难以同时兼顾两个维度。改善归一化处理方法可以优化这个问题,但会让部分重叠区域区分度降低。

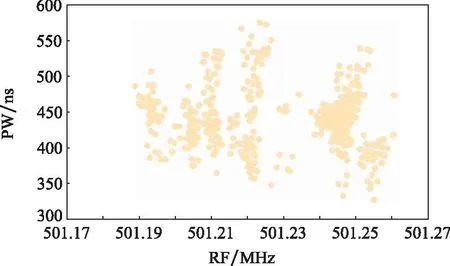
图14 空间域的标准化问题Fig.14 Standardization problem of spatial domain

3.2 多参数优化问题

本研究所述方法涉及4个参数:空间半径R,时间区域ΔT,最低点数Pmin和标准化参数δ。判断密度的核心是根据时空邻域中样本数量与最低点数Pmin的关系,同时涉及4个参数的调整。因此,如何获取各参数的联合最优解是一个可以改进的方向,可考虑对“密度”进行新的定义来解决。

3.3 IoU阈值选取问题

使用IoU方法需设置三维矩形框范围和IoU阈值,若阈值设置过高会导致数据点丢失,设置过低则会导致噪声点增多。通过改进自适应阈值选取方法可以有效改善这一问题。

3.4 多维IoU定义问题

由于不同维度信息数据的尺度和分布不同,在数据标准化时比例不同,导致各数据维度对IoU数值的贡献有所差异。因此,需要根据实际情况适度修正多维空间内IoU,使结果更优。

随着加入特征数量的增多,并集部分所占比重越来越低,使得新加入特征的边际效应持续递减,可以通过优化多维空间中IoU计算方法来改进这一问题。

4 结 论

本文提出了一种基于时空密度聚类和三维IoU的辐射源PDW信号两级分选方法。一级分选采用TOA-RF-PW三类参数,构建时空密度聚类模型进行分选。二级分选在一级分选的基础上,使用三维IoU方法在TOA-RF-PA三维空间内进行优化,提升了分选准确率。本文分别采用仿真数据和实际数据进行实验,最终分选结果的各簇内部经可视化验证均呈现正弦调制的包络特征,符合单一PDW辐射源特征规律,验证了该分选方法的有效性。

该方法改善了传统PRI分选法面对复杂辐射源信号的分选能力弱的局限性,但目前只适用于常规辐射源,针对捷变型等辐射源需开展进一步研究。