无频间钟偏差改正的BDS-2三频非组合PPP随机模型优化

周长江,余海锋,王林伟,雷云平,岳彩亚

(1. 中水北方勘测设计研究有限责任公司,天津 300222; 2. 山西省国土空间调查规划中心, 山西 太原 030000; 3. 聊城大学地理与环境学院,山东 聊城 252000)

随着计算机、通信和芯片等软硬件设备的不断升级和发展,多个全球导航卫星系统(GNSS)已具备播发多频观测数据的能力,为消除或减弱电离层延迟影响、抑制观测噪声放大提供了新方法,同时也为增强卫星定位几何强度和解算容错率提供了基础支撑[1-3]。然而,由于当前国际GNSS服务组织(IGS)分析中心发布的钟差产品中包含了无电离层组合的卫星端相位硬件延迟时变部分,导致当钟差产品被用到第3个频率时,使得全球定位系统(GPS)和北斗二号卫星系统(BDS-2)精密单点定位(PPP)验后残差出现较大波动,需要额外的处理频点之间的偏差,称为频间钟偏差(inter-frequency clock deviation,IFCB)[4]。相关研究已证明GPS Block IIF和BDS-2卫星IFCB变化量级最大可分别达30 cm和5 cm,这对于验后残差仅在厘米级的PPP技术而言必须加以改正[5]。为此,文献[6-8]提出了两个无电离层组合做差的历元间差分方法、星间历元间差分方法以及常数部分和时变部分分开解算的方法估计IFCB。利用上述估计的IFCB可直接用于PPP事后解算模型改正中,或是通过对IFCB建立预报模型进行实时多频PPP或PPP网解,相关结论已证明基于上述IFCB建模改正方法可较好地满足GPS Block IIF卫星多频精密定位。

而对于BDS-2卫星的IFCB,由于其影响量级相对较小,当利用上述方法进行IFCB建模改正时精度提升有限,并且会增强多频PPP计算负担[9]。为此,众多学者在处理BDS-2三频非组合PPP时,主要倾向于不加IFCB改正,且将3个频率载波观测值权重设置成相等或根据经验降低第三频率观测值权重。因此,为了客观评估无IFCB改正时BDS-2三频非组合PPP最优随机模型和提升多频观测数据融合定位性能,本文提出一种枚举方法重点分析当无IFCB改正时,BDS-2第三频率观测值权重的最优取值,并进行三频非组合PPP静态和动态定位性能验证。

1 BDS-2三频非组合PPP随机模型优化

1.1 三频非组合PPP定位模型

原始多频(j=1,2,3,…)非差伪距和载波相位观测方程可表示[10-11]为

(1)

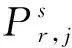
(2)

基于式(2),文献[13]将接收机钟差表达成了同种方式并进行了多频非组合PPP推导。为了突出重点,本文直接给出了顾及IFCB的BDS-2三频非组合PPP伪距和相位观测方程实用公式,为

(3)

(4)

(5)

(6)

1.2 随机模型优化

文献[9]已证明在附有IFCB约束的条件下BDS-2三频非组合PPP定位性能得到小幅度提升,但需提前估计IFCB,增加了程序计算负担和时间。因此,本文重点在未顾及IFCB对第三频率观测值改正的情况下,提出一种载波相位观测值权重枚举方法,分析并评估第三频率载波相位观测值与前两个频率观测值最优权比配置方法,以实现BDS-2三频非组合PPP随机模型优化。即

(7)

表1 不同方案下c的取值

图1 MGEX跟踪站分布

图2 不同方案下2小时PPP解坐标残差

2 试验结果与分析

为了进一步验证BDS-2三频非组合PPP优化随机模型的可用性,本文基于3种方案分别实施了亚太地区6个测站三频非组合PPP静态和动态解算。其中,方案1为无IFCB改正的BDS-2三频非组合PPP;方案2为基于真实IFCB改正值的三频非组合PPP;方案3为将c取值为3.0,既将第三频率载波相位观测值的权重降低3倍。表2中给出了6个测站的详细信息,均可正常接收BDS-2观测值,数据采样率为30 s,其他解算参数配置与随机模型优化部分完全一致。值得说明的是用于性能验证的6个测站并未参与随机模型优化评估。

表2 各MEGX测站详细信息

2.1 BDS-2三频非组合PPP静态定位性能验证

图3中以CUT0站和NNOR站为例,展示了不同方案下的BDS-2三频非组合PPP坐标残差序列。整体分析可知,方案2和方案3的时间序列残差基本重合,说明将BDS-2第三频率权重降低为原来的3倍具有与采用真实IFCB改正同等的定位效果,且方案2和方案3坐标残差序列均优于方案1,特别是在初始收敛阶段。

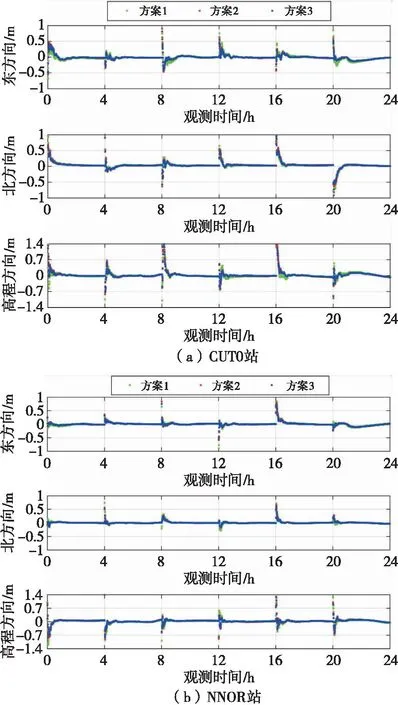
图3 CUT0站和NNOR站不同方案BDS-2 三频非组合PPP残差序列

为了详细分析不同方案下坐标解算精度差异,将每个测站分为6个弧段,并详细统计了所有测站36个弧段坐标定位精度,统计时以IGS发布的SNX文件中的各测站坐标作为真值[15],将每个弧段最后半小时坐标残差取平均作为解算精度,进而消除异常历元对统计精度的影响。表3中给出了3种方案下所有弧段PPP解算坐标平均残差,分析可知,当顾及IFCB影响条件下BDS-2三频非组合PPP定位精度可得到进一步提升,对于方案1和方案3,当BDS-2第三频率权重降低为原来的3倍时,坐标解算精度在东、北和高程方向分别可提升10.1%、5.7%和7.1%。对于方案2和方案3,定位精度基本一致。

表3 不同方案BDS-2三频非组合PPP平均残差和收敛时间

为了分析优化的BDS-2三频非组合PPP随机模型对收敛时间的改善,表3中同样统计所有弧段收敛到10 cm所用的时间。其中,收敛时间定义为坐标东、北和高程方向坐标残差均收敛到10 cm以内所用的时间,且在后续历元保持稳定。为了能得到客观的收敛时间,本文在对36个弧段收敛时间平均时,以3倍的中误差作为阈值进行异常值的剔除。对表3分析可知,当顾及IFCB的影响时,可进一步提升坐标残差收敛速度。其中,相对于方案1,采用方案2和方案3进行PPP解算时,在东、北和高程方向可分别提升约11.0、4.8和9.2 min,并且同样展示出了方案2和方案3具有同等效果的收敛速度提升。

2.2 BDS-2三频非组合PPP动态性能验证

为了验证优化的BDS-2三频非组合PPP随机模型的动态定位性能,分别基于3种方案实施了6个测站动态解算,坐标的过程噪声均方误差设置为60 m。限于篇幅,图4中仅以JFNG站为例展示了该点定位残差,表4中统计了6个测站平均均方根误差(RMS)。整体分析可知,3种方案下均可实现厘米级定位精度,方案2和方案3定位残差序列具有较高的重合度,说明此两种方案动态定位结果较为接近,且均优于方案1。基于表4进一步分析可知,相对于方案1,在顾及IFCB影响的情况下,方案2和方案3均可实现坐标精度小幅度改善,而方案2和方案3定位精度则表现得基本一致。通过统计平均RMS值可知,相对于方案1,当采用降低第三频率相位观测值权重的方法时,可分别实现东、北和高程方向10.7%、6.1%和9.2%的精度提升。

图4 JFNG站不同方案BDS-2三频动态非组合PPP时间序列

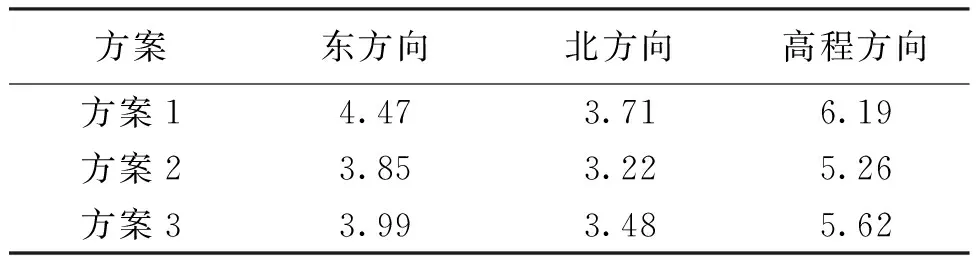
表4 不同方案BDS-2三频非组合PPP动态残差平均RMS cm

3 结 语

本文针对BDS-2传统钟差产品无法直接应用于多频精密单点定位的问题,提出了一种BDS-2三频非组合PPP随机模型优化方法,并通过亚太地区大量MGEX跟踪站实测数据进行验证。结果表明,当无IFCB改正时,可将第三频率相位观测值方差放大到原始方差的2～4倍。为了进一步验证优化的随机模型,基于亚太地区6个MGEX站分别实施了无IFCB改正,利用真实IFCB改正和将第三频率相位观测值方差放大到原始值3倍的BDS-2三频非组合PPP动态和静态解。结果表明,无论是动态解还是静态解,当顾及IFCB影响的情况下均可实现定位精度和收敛速度改善,相对于采用真实IFCB改正,采用将BDS-2第三频率观测值权重降低为原来3倍的方法基本具有同等PPP性能改善,但可避免对IFCB进行事前估计的问题。