基于图卷积神经网络的道路网匹配

齐 杰,王中辉,李驿言

(1. 兰州交通大学测绘与地理信息学院,甘肃 兰州 730070; 2. 地理国情监测技术应用国家地方联合工程研究中心,甘肃 兰州 730070;3. 甘肃省地理国情监测工程实验室,甘肃 兰州 730070)

数字化的道路数据是对实体道路的抽象化表达,是基础地理数据库重要的组成部分[1]。随着道路的不断变化,道路网数据的快速更新成为一个亟待解决的问题,而道路网匹配是道路网数据变化检测和增量式更新的前提与关键技术,更是实现地图自动综合的必然要求。

道路网匹配一般通过计算道路的语义相似性和几何相似性进行匹配。基于语义相似性的匹配方法主要通过计算线要素之间的语义相似性进行道路网匹配[2-4],很大程度上依赖于属性信息的唯一性。而多源道路数据往往缺少具有唯一性的属性信息,因此该方法只能用于辅助匹配。基于几何相似性的匹配方法通过计算线要素之间的几何相似性进行道路网匹配[5-7]。几何相似性包括方向、距离、形状、拓扑关系等相似性度量指标,通常选取一种或多种相似性度量指标,确定指标之间的权重组合,选择合适的相似度匹配阈值,完成道路网的匹配。该方法通常采用主观赋权法进行相似性指标权重组合和匹配阈值确定,对匹配结果具有较大影响。

图卷积神经网络(GCN)是目前最常用的图数据深度学习网络,具有自动提取局部空间特征的能力,从而减少了人工特征工程的构建过程,实现了数据端到端的预测。目前,GCN在道路网模式识别领域得到了重要的应用[8-9]。鉴于此,本文针对现有道路网匹配方法中相似性度量因子之间的权值分配和匹配阈值确定方法的不足,结合图卷积神经网络,提出一种道路网匹配方法。

1 图卷积神经网络的基本原理

文献[10]基于图谱理论从卷积定理出发,在谱空间定义图卷积,首次提出基于频域的图卷积神经网络。文献[11]用切比雪夫展开多项式参数化卷积核,实现谱卷积神经网络,从而避免拉普拉斯矩阵的特征分解,加速特征矩阵的求解。文献[12]通过限制Cheb Net的图卷积操作在一阶邻域内执行,大大提高了计算效率。

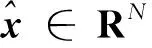
(1)

图傅里叶的逆变换为

(2)

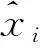
图结构数据的节点排列不均匀,邻域结构不固定,不能满足平移不变性,无法定义节点域的卷积运算。模仿离散时间信号处理中的卷积借助傅里叶变换,将图的卷积运算转换为谱域中傅里叶变换的点乘运算,公式为

f*g=F-1[F(f)⊙F(g)]=Q[(QTg)⊙(QTf)]

(3)

式中,⊙为哈达玛积,指两个矩阵(或向量)的逐点乘积;f为特征函数;g为卷积核。如果把QTg整体看作可学习的卷积核,记为gθ,则图卷积公式为

σ=QgθQTf

(4)

基本的频域卷积网络要计算拉普拉斯矩阵所有的特征值和特征向量,计算量大。切比雪夫多项式(Chebyshev polynomials)可加速特征矩阵的求解。Cheb Net通过对拉普拉斯矩阵进行泰勒展开定义图滤波器,其卷积层定义为

(5)

通过K控制滤波器的复杂度,可极大地降低过拟合风险。但是由于在进行矩阵特征分解时具有较高的时间复杂度,计算效率低,因此在实际应用中效率较低。

文献[12]通过限制式(5)中的K=1,定义第l层的卷积运算,即

(6)

2 基于图卷积神经网络的道路网匹配

将待匹配道路网数据转化为对偶图,利用对偶图将道路构建为图结构数据,将节点所代表的两条道路是否为匹配道路作为标签,输入GCN模型中进行训练,完成道路网的匹配。模型框架如图1所示,主要包括以下步骤:①数据处理,对数据进行预处理,确定待匹配道路的候选匹配集;②特征提取,选取长度相似性、距离相似性、方向相似性、拓扑相似性4个特征因子作为对偶图节点的特征;③GCN学习,先构建对偶图,并对道路网标注标签,再以图数据转化后的对偶图作为输入数据,利用卷积运算提取特征,通过反复迭代最终使模型达到收敛。

图1 基于图卷积神经网络的道路网匹配整体框架

2.1 数据处理

将获取的数据利用ArcGIS进行拓扑检测和属性表检查,对重复路段和孤立路段进行删除,统一两个地图数据的坐标系。对可匹配道路进行节点数量的检查,为满足后续对待匹配路段和参考路段进行图结构构建,需要在不影响道路整体结构的前提下对道路进行增加或删除节点的处理,使节点的数量达到一致。利用缓冲区增长法确定待匹配道路的候选匹配集。

2.2 特征提取

为了度量待匹配的两弧段的相似性,定义如下相似特征的度量指标,作为后续卷积运算的特征参量。

2.2.1 长度相似性

参考路段的几何长度和待匹配路段的几何长度的相似程度,公式为

(7)

式中,LA、LB为道路A、B的长度;min()为获取最小值函数;max()为获取最大值函数,余同。

2.2.2 距离相似性

参考路段与待匹配路段的距离相似程度,采用两线要素之间的有向Hausdorff距离进行计算,距离越近相似度越高。计算方法为,若待匹配道路A上的节点集合为P(p1,p2,…,pn),对于集合P上的任意一点pi(Xi,Yi),作点pi到参考道路B的垂线;若垂线与道路A相交,即垂足在道路B上,则采用垂直距离;若垂足不在道路B上,而在道路B的延长线上,则采用节点间的欧式距离[13]。距离相似性公式为

(8)

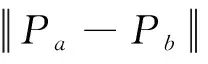
2.2.3 方向相似性

参考路段和待匹配路段在道路走向上的相似程度,采用方向角计算方向的相似程度,公式为

(9)

式中,Sori表示道路A、B方向相似度;OriA、OriB表示道路A、B的方向。

2.2.4 拓扑相似性

采用节点连通度对拓扑相似性进行描述。节点的连通度即道路节点关联弧段的数量[14],见表1。道路A、B的拓扑相似度可表示为

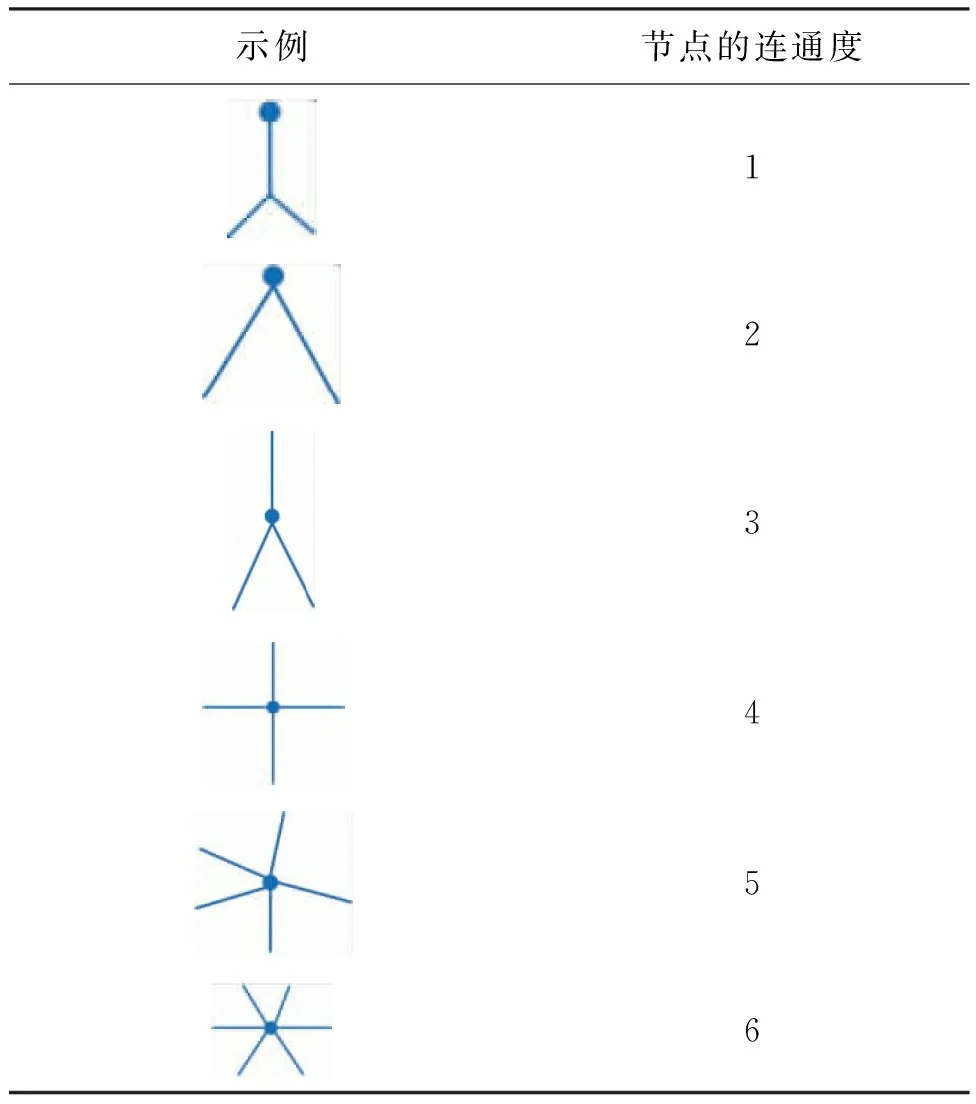
表1 节点连通度示意

(10)

式中,CA、CB表示道路A、B收尾节点的连通度的和。

2.3 GCN学习

2.3.1 道路网对偶图构建

对道路网数据进行预处理后,需要将道路网数据构建为图结构,使之符合图卷积神经网络对输入数据的结构形式要求。现有的图卷积方法都是针对节点的分类或图分类,因此选择道路作为节点,道路之间的连接关系作为边,将道路网抽象为对偶图。试验在进行道路网匹配时是在两个数据集上进行的计算,因此在进行对偶图构建的过程中,将两个数据集中待判断是否匹配的道路抽象表示在一张对偶图上,每个节点所提取的特征因子即为两条道路之间的相似性度量。如图2所示,将待匹配道路A和参考道路B抽象为一个对偶图C。其中,C1为道路L1和道路M1所抽象的对偶图节点,C1提取的特征因子即为道路L1和道路M1之间各相似性度量因子的计算值,C2和C3同理。因此,将道路网匹配问题转化为节点的分类问题,输出为0或1,0表示不能匹配道路,1表示可匹配道路。

2.3.2 图卷积网络模型构建

道路网匹配任务的标注、输入和输出如下。

(1)标注:y∈{0,1}。标签值为1,则说明该对偶图所对应的两条道路为匹配道路;反之,标签值为0,则说明该对偶图所对应的两条道路为不匹配道路。

(2)输入:将数据集转化为对偶图,把道路的路段作为图的节点,连接关系作为图的边,最终得到的道路网图模型G=(V,E,A)。每个图模型都包含N个节点,每个节点都有4个计算特征值{f1,f2,f3,f4},分别对应长度相似性、距离相似性、方向相似性、拓扑相似性。所有节点构成N×4的特征向量和一个N×N的邻接矩阵。

模型分为输入层、卷积层、输出层3部分,如图3所示。

3 试验与分析

考虑不同地区自然地理环境和经济发展水平不同,其道路网类型也各有不同。当前道路网的类型可以被归纳为方格网式、环状放射式、自由式、混合式4种。为验证本文方法的合理性和普适性,选取较为常见的方格网式道路和环状放射道路,在同尺度和多尺度下进行道路网匹配试验。如图4所示,方格网式道路共有1410条待匹配道路,环形放射式道路共有920条待匹配道路。将待匹配道路和参考道路构建为对偶图,完成标注后作为试验样本。将试验样本按8∶2的比例划分为训练样本和测试样本。

图4 不同尺度下的两种类型道路网

如图5所示,选取不同卷积层数和不同的卷积核,所得到的匹配精度和曲线拟合速度不同。综合分析,试验最终使用的图卷积模型由4个卷积层和1个输出层组成,每个卷积层包含64个卷积核。将ReLU作为激活函数、Adam作为优化器进行参数更新,设置学习率为0.005,L2正则化参数为0.000 5。模型经过400次迭代达到收敛,损失值基本不再发生变化。

为验证模型的合理性和普适性,通过计算匹配的准确率P和召回率R,评价道路网的匹配质量[15],公式为

(11)

(12)

式中,S为道路总数;M为存在匹配关系的道路数量;C为正确匹配的道路数量。

为了同时考虑道路网的匹配率和召回率,避免因匹配率和召回率相反变化引起的描述与评价不便,采用匹配准确率和召回率的调和平均值F进行结果的评价[16],公式为

(13)

式中,P为准确率;R为召回率。

匹配试验的迭代过程如图6所示,同尺度方格网式道路、同尺度环状放射道路,以及不同尺度方格网式道路、不同尺度环状放射道路的匹配结果,具体见表2。

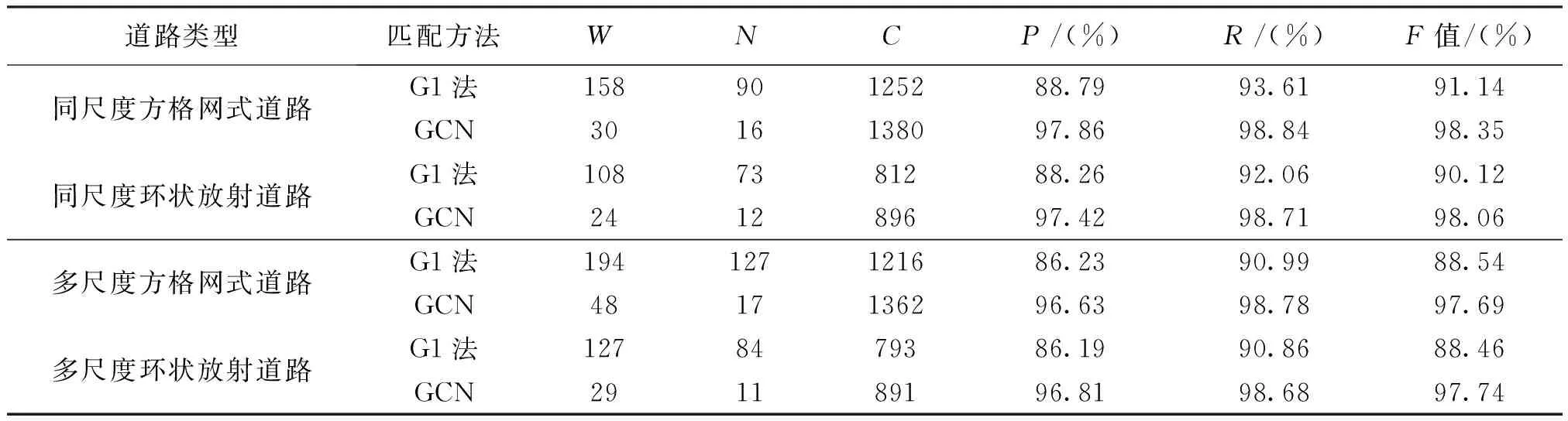
表2 不同试验数据下道路网匹配结果

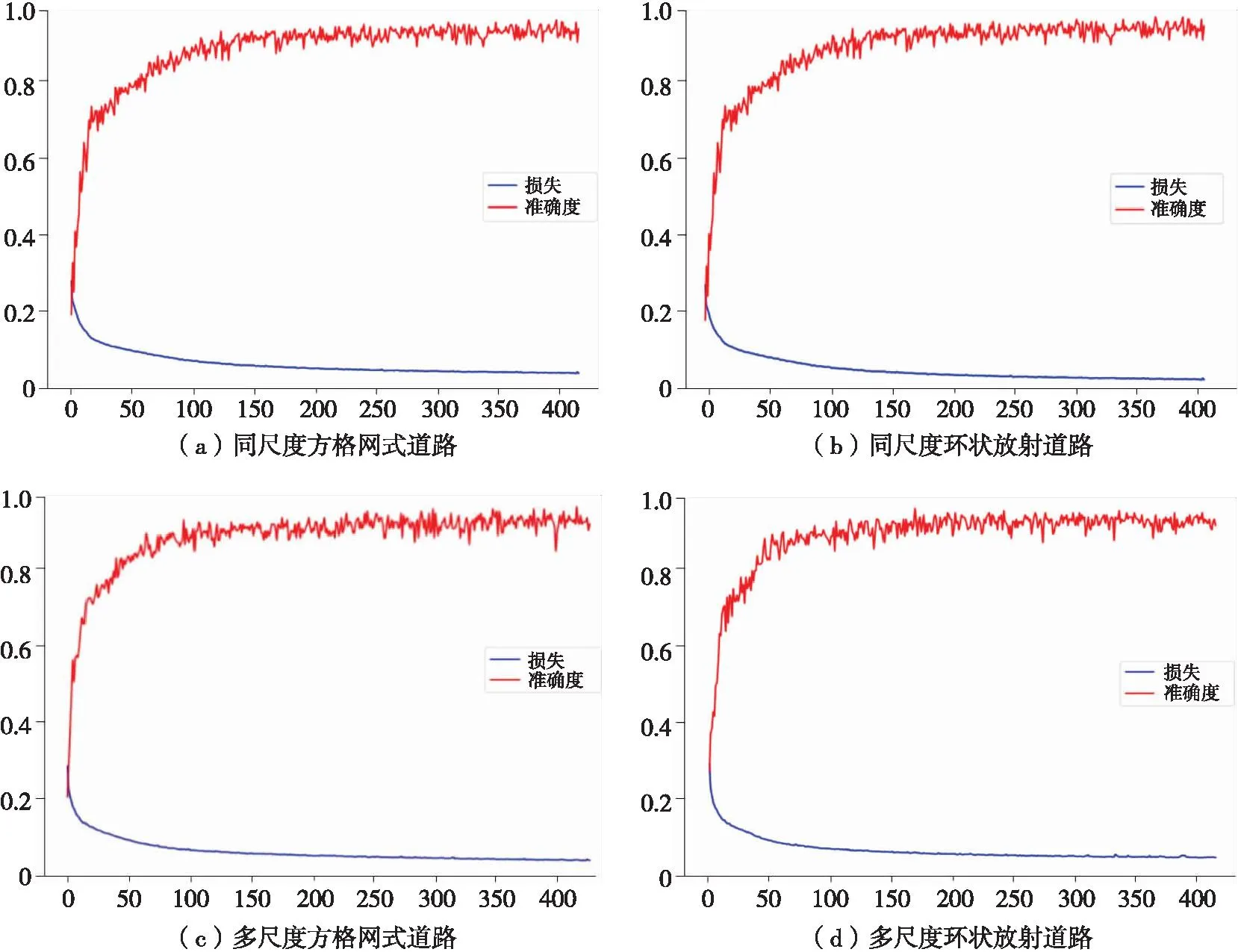
图6 匹配试验的损失与准确度变化

对试验结果进行分析可知:

(1)两种方法在同尺度下的匹配结果均优于多尺度下的匹配结果。比例尺相同的两幅地图采集数据与制作地图时的精度相同,特别是在环岛、立交等较为复杂的道路上表现尤为明显。在大比例尺数据中这部分道路被完整刻画,而在小比例尺道路数据上会被简化甚至删除,这就造成在相同比例尺道路上能够成功匹配的复杂道路在不同比例尺上极易产生辅路与主路无匹配的情况,从而导致在不同比例尺道路匹配的结果低于在相同比例尺道路上匹配的结果。

(2)同尺度下方格网式道路的匹配结果优于环状放射式道路的匹配结果。这是由于方格网式道路网中多为平行或垂直的直线型道路,结构较为简单,而环形道路网中曲线型道路数量较多,两条可匹配道路之间部分路段的差异性较大,导致匹配结果产生误差。而在多尺度下环状结果却优于方格网式,对数据进行统计分析发现,方格网式道路中复杂道路尤其是环岛类型路段的数量多于环状道路,这使得最终的匹配结果出现了不同的变化。

(3)G1法的匹配率和召回率在同尺度方格网式道路数据中最高,分别达到88.79%和93.61%;在不同尺度环状放射道路最低,只有86.19%、90.86%。这主要是由于G1法是一种主观赋权法,主要依据专家的经验赋予各个相似性度量因子之间的权值,具有一定的主观性。而GCN的方法中匹配率和召回率最低的也达到96.63%、98.68%,F值最低为97.69%,相较于G1法具有更好的匹配精度。

4 结 语

本文提出了一种基于图卷积神经网络的道路网匹配方法,在进行监督分类学习后,利用反向传播机制,自动调整权重和阈值,完成道路网的匹配。试验结果表明,该方法具有以下优势:①可以自动对相似性度量因子进行权重赋值,有效降低了由主观赋值导致的匹配错误,提高了匹配精度;②可以自动确定匹配阈值,无须人为设定初始匹配阈值和经过反复试验调整阈值,提高了匹配效率。

但图卷积神经网络叠加多层会出现过拟合现象,使模型产生退化,从而导致过于简化的复杂路段的局部特征相似度较低,产生错误匹配的情况。下一步工作考虑采取残差网络等复杂网络结构,增加网络深度,提高匹配精度。