三弧段等距型面设计参数计算研究

廖鹏，张虞，刘飞，马宪智

（中国船舶集团有限公司 第七〇三研究所 无锡分部，江苏 无锡 214151）

0 引言

三弧段等距型面属于型面联接的一种，这种联接属于无键联接[1]。等距型面联接的主要优点：1）能够自动定心；2）无应力集中；3）轴、轮毂及动力传递部分强度高；4）各方向具有等尺寸性，测量方便；5）廓形曲线为圆弧，便于加工[2]。这种联接结构适合在高转速、大转矩、安装空间要求小和振动要求高的场合使用。国外将该结构广泛应用于机床、矿山机械、高速水力测功器等领域[3]。近年来，国内学者对三弧段等距型面联接做了大量研究：郑友益等[4]对三弧段等距型面曲线方程和旋轮线型面曲线方程做了详细推导，并从测量方便的角度得出三弧段等距型面曲线比旋轮线型面曲线更优越的结论；王德胜等[5]通过几何关系研究了三弧段等距型面型面公差配合的影响因素，并给出了选用原则；杜可可等[6]基于三弧段等距型面结构分析，应用CAD/CAM软件得到了三弧段等距型面图形、轮廓刀具路径及NC数控加工程序，并实施了实体切削仿真；吕宝占等[7]基于等距型面工作原理，导出了三弧段等距型面轴强度近似计算方法，该方法简单、方便，能够满足工程需要；王德胜等[8]介绍了三弧段等距型面工作表面挤压应力的计算公式与三弧段等距型面联接挤压强度的验算条件，并通过应用实例分析了三弧段等距型面孔与轴的工艺性；以上研究主要集中于轮廓曲线方程推导、强度验算、型面公差配合选用、数控加工等方面，而对于三弧段等距型面曲线参数计算的研究很少。廖鹏等[9]提出了最大距离比较模型及最小二乘模型，采用该模型得到了某型水力测功器主轴三弧段等距型面拟合曲线及其设计参数，但参数计算过程较为繁琐。因此，找到一种更为简单的参数计算方法有重要的科学意义和应用前景。

本文首先分别介绍了三弧段等距型面曲线的成型原理、曲线方程，再针对某型高速水力测功器主轴三弧段等距型面曲线实际测点，通过提出的简单参数计算方法，得到了某型高速水力测功器主轴三弧段等距型面拟合曲线及其设计参数。三弧段等距型面拟合曲线理论坐标点与实际测点吻合程度高，验证了本文提出方法的准确性，为今后某型高速水力测功器主轴三弧段等距型面的加工设计提供参考。

1 三弧段等距型面曲线

1.1 三弧段等距型面曲线成型原理

如图1所示，三弧段等距型面曲线中心位于坐标系原点o，其由3组半径为r1、r2的圆弧依次相切组成，3组圆弧圆心在半径为7.5e（e为偏心量）的圆上，且互成120°。三弧段等距型面曲线内切圆直径为d3，外切圆直径为d2，任意两条相切于该廓形曲线的平行线之间的距离均等于d1（d1为等距值）。其中，半径7.5e的圆称为三弧段等距型面曲线的基圆，r1为大圆弧半径，r2为小圆弧半径。

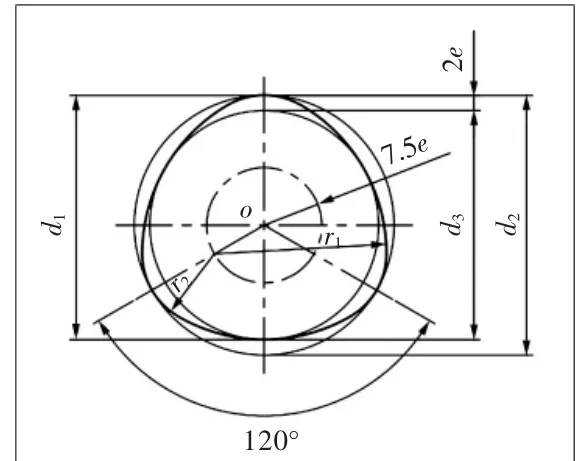
图1 三弧段等距型面曲线图

图1中各参数存在如下关系：

1.2 三弧段等距型面曲线方程

建立xoy坐标系，如图2所示，三弧段等距型面曲线方程[10]为:

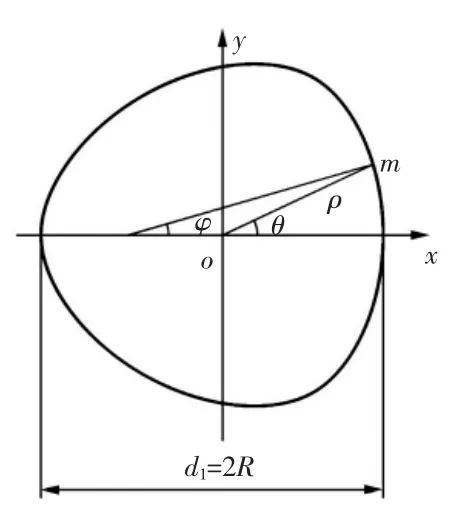
图2 三弧段等距型面曲线方程

式中：R为平均半径；e为偏心量；φ为角参数，即三弧段等距型面曲线上任意一点m的法线与x轴之间的夹角，0≤φ≤2π。

以o为原点，ox为极轴，则三弧段等距型面曲线的极坐标方程为：

对于三弧段等距型面曲线，其基本参数为R和e，R主要影响廓形曲线的轮廓大小，e主要影响廓形曲线的形状。

2 三弧段等距型面曲线拟合

2.1 三弧段等距型面曲线设计参数计算

已知某型大功率高速水力测功器主轴三弧段等距型面曲线实际测点，如图3所示，现需确定该轴三弧段等距型面曲线参数。根据式（1），三弧段等距型面曲线内切圆直径d3与外切圆直径d2可通过作图求出，偏心量e按式（4）计算得到：

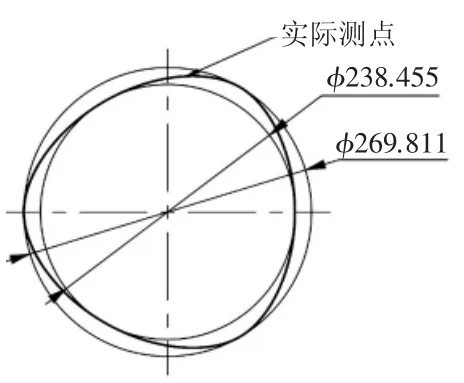
图3 三弧段等距型面曲线实际测点

通过式（1）计算得到等距值d1，平均半径R计算公式为

计算结果如表1所示。

表1 参数计算结果

至此，三弧段等距型面曲线设计参数均已获得。

2.2 三弧段等距型面曲线实际测点数据处理

由三弧段等距型面曲线极坐标方程可以看出，对于任意给定的角参数φ，都能计算得到相应的极角θ和极径ρ，极角θ和极径ρ存在一一对应的关系，但无法直接给出极径ρ关于极角θ的方程。这给三弧段等距型面拟合曲线理论坐标点与实际测点的比较带来了困难。因此，有必要对三弧段等距型面曲线的实际测点进行数据处理。

通过三坐标测量仪，可以得到某型大功率高速水力测功器主轴三弧段等距型面曲线（任意截面）实际测点，得到的数据是各个测点的平面坐标值（x，y），三弧段等距型面曲线实际测点的极径ρ1和极角θ1计算公式为：

式中，极角θ1计算结果在［-π/2，π/2］范围内变化。而式（3）中极角θ的变化范围为［0，2π］，因此需要让三弧段等距型面曲线实际测点的极角θ1也在［0，2π］范围内变动。根据正切函数y=tan x的曲线特点，将三弧段等距型面曲线实际测点按所在象限分为A、B、C三组，通过编程实现将三弧段等距型面曲线实际测点的极角θ1在［0，2π］范围内变动。

由于某型大功率高速水力测功器主轴在使用过程中出现局部变形或机械加工偏差过大，三弧段等距型面曲线（任意截面）实际测点所形成的轨迹趋势与理论曲线趋势会存在一定偏差，这种偏差导致通过三弧段等距型面曲线（任意截面）实际测点计算得到的极角会出现失真的情况，即：在第一象限内，随着三弧段等距型面曲线实际测点坐标x值的减小，极角反而减小。因此需要排除这些失真测点。在得到三弧段等距型面曲线实际测点极角θ1的情况下，通过编程将三弧段等距型面曲线实际测点极角θ1中的失真测点排除。

由式（3）可知，三弧段等距型面曲线实际测点的极角、极径方程属于关于参数φ的参数方程，由于该方程不管是通过极径还是极角都难以直接求解参数φ，若想通过参数φ在三弧段等距型面拟合曲线理论坐标点与实际测点之间建立联系将显得非常困难，因此需要寻求其它的方法来解决这一难题。这里，由于目前已经得到三弧段等距型面曲线实际测点的极径、极角值，而三弧段等距型面拟合曲线理论坐标点的极径、极角值可以通过更改计算步长的办法得到，为了保证三弧段等距型面拟合曲线理论坐标点的极径、极角值能够覆盖三弧段等距型面曲线实际测点的极径、极角值，计算步长的取值可以尽可能地小，这里取0.001。当找到三弧段等距型面拟合曲线理论坐标点与实际测点相同的极角值时，两者对应的极径差值即可求出。在寻找三弧段等距型面拟合曲线理论坐标点与实际测点的相同极角值时，需要设定一个误差范围，保证能够收敛，并且这个误差范围是可以接受的，这里我们取误差范围delta的值小于0.000 014。通过编程筛选出三弧段等距型面拟合曲线理论坐标点与实际测点的相同极角值。

通过上述得到的三弧段等距型面拟合曲线理论坐标点与实际测点的极径值，可以得到三弧段等距型面拟合曲线理论坐标点极径ρ0与实际测点极径ρ差值随角度θ变化的关系曲线（如图4），以及三弧段等距型面拟合曲线理论坐标点极径ρ0相对误差ε随角度θ变化的关系曲线（如图5）。三弧段等距型面拟合曲线理论坐标点极径ρ0相对误差ε计算公式为

图4 拟合曲线与测点极径差值随角度变化曲线

图5 拟合曲线极径相对误差随角度变化曲线

从图4可以看出，三弧段等距型面拟合曲线理论坐标点与实际测点基本吻合，两者极径差值随角度在-0.09～0.02 mm范围内变化。角度在0°～60°范围内，三弧段等距型面拟合曲线理论坐标点与实际测点极径差值随着角度的增大而增大；角度在60°～250°范围内，三弧段等距型面拟合曲线理论坐标点与实际测点极径差值随角度的增大而呈减小趋势，在160°～180°范围内，三弧段等距型面拟合曲线理论坐标点与实际测点极径差值随角度的增大而增大，原因可能是某型高速水力测功器主轴三弧段等距型面在180° 位置附近由于受力变形或者加工偏差过大；角度在250°～360°范围内，三弧段等距型面拟合曲线理论坐标点与实际测点极径差值随角度的增大而增大。理论上，对于一根未投入使用的三弧段等距型面轴而言，拟合曲线理论坐标点与实际测点极径差值与角度呈周期性变化关系，在图4中，添加ρ0－ρ=0.035水平线，图4曲线近似呈周期性变化，因此，本文针对三弧段等距型面参数计算所采用的方法准确，可为今后某型大功率高速水力测功器主轴三弧段等距型面的加工设计提供参考。

从图5可以看出，三弧段等距型面拟合曲线理论坐标点极径相对误差基本控制在0.09%以内，三弧段等距型面拟合曲线理论坐标点极径相对误差的变化趋势与图4曲线变化趋势基本一致，误差满足工程需要，进一步说明本文采用的参数计算方法准确可靠，所得到的参数可以作为某型高速水力测功器三弧段等距型面曲线的设计参数。

3 结语

本文介绍了三弧段等距型面曲线的成型原理、曲线方程，选取某型大功率高速水力测功器主轴三弧段等距型面曲线测点作为研究对象，提出一种简单的参数计算方法，通过该方法得到了三弧段等距型面曲线偏心量、等距值等设计参数，再通过极坐标方程得到三弧段等距型面拟合曲线理论坐标点。

经与实际测点对比分析，得出如下结论：1）得到了某型大功率高速水力测功器三弧段等距型面拟合曲线理论坐标点及其设计参数，以期为高速水力测功器主轴的加工设计提供参考；2）三弧段等距型面拟合曲线理论坐标点与实际测点基本吻合，两者极径差值随角度在-0.09～0.02 mm范围内变化，变化趋势呈先增、后减、再增，曲线近似呈周期性变化，说明本文采用的方法准确可靠；3）在160°～180°范围内，三弧段等距型面拟合曲线理论坐标点与实际测点极径差值随角度的增大而增大，原因可能是某型高速水力测功器主轴三弧段等距型面在180°位置附近受力变形或加工偏差过大；4）三弧段等距型面拟合曲线理论坐标点极径相对误差基本控制在0.09%以内，变化趋势与极径差值曲线基本一致，误差满足工程需要，说明本文采用的参数计算方法准确可靠，所得到的参数可以作为某型高速水力测功器三弧段等距型面曲线的设计参数。