区域地理加权回归分析方法

王增铮,张福浩,,赵阳阳,仇阿根

(1. 西南交通大学地球科学与环境工程学院,四川 成都 611756; 2. 中国测绘科学研究院地理空间大数据应用研究中心,北京 100036)

地理加权回归(GWR)的提出有效地探测了空间非平稳特征,丰富了空间分析方法[1]。20多年来,国内外学者基于传统GWR方法,从交叉验证[2]、异方差剔除[3]、稳健估计[4]、时空特征探测[5-6]等方面发展了该方法,并广泛应用到大气反演[7]、疾病预测[8]、城市景观[9]、房价估算[10-12]等多个自然社会领域。根据传统GWR原理,空间权重是核心,反映了观测点对回归点的影响程度。

空间异质性是指过程和关系在空间上的变化[13],是地理学、生态学及空间分析中的一个重要概念,被视为局部统计的基础[14]。空间异质性分为连续异质性和离散异质性[15],对两者的精确解算是空间回归分析能否揭示地理要素之间复杂的相互关系的决定性因素。在回归模型中,空间异质性的存在要求回归系数在空间上变化,即在空间不同单元之间离散变化或在空间上连续变化[16]。以往的空间回归分析关注了空间离散异质性,却对空间的连续性考虑不够,遗漏了一些重要的局部变化[16-17]。GWR建立在“临近相关,距离越远相关性越小”的假设前提下,这种方法是对空间连续异质性的有效探测[16]。

但在现实中,受空间离散异质性的影响,空间距离相近的事务,属性也会相差较远[18]。特别是在社会经济领域,受区划因素的影响,距离相近的事物,属性可能相差较远。如商品房屋价格受区域政策和学区影响,即使两个小区距离很近,价格也会相差很大。传统的GWR方法仅考虑空间距离,但未考虑离散异质性导致的离散异质区的区域距离,这导致区域临界处拟合不充分[19]。本文综合考虑在GWR的空间核函数中增加区域判别,提出区域地理加权回归方法(regionally geographic weighted regression, RGWR),通过构建区域空间权重计算策略有效筛选观测点,修正核函数,优化权重计算方法,在探测空间非平稳性的同时探测空间离散异质性。

1 区域地理加权回归分析方法

1.1 地理加权回归方法

GWR在多元线性回归基础上,把位置参数嵌入回归系数中[20],公式为

(1)

式中,(ui,vi)为第i个观测点的坐标位置;βk(ui,vi)为第i个观测点的第k个回归系数;εi～N(0,σ2),Cov(εi,εj)=0(i≠j)。

1.2 区域地理加权回归分析方法

RGWR是GWR的一个扩展,用于探索空间非平稳和空间离散异质性,其基本思路是通过向GWR中添加区域变量,将地理位置嵌入回归系数中,允许每个单独的点具有不同的值以估计回归系数,且受每个回归点的空间离散异质区域的影响[18]。模型可表示为

(2)

在估计采样点i的回归系数时,在GWR的基础上添加了区域因子,因此当观测点位于区域范围之外时,该点参与回归的权重除了受空间权重矩阵的影响,还受区域因子的影响。同样使用局部最小二乘法,点i处的回归系数估计值计算公式为

(3)

区域空间权重矩阵RWi表示为

(4)

式中,rwij表示观测点对回归点的区域空间权重。

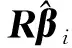
(5)

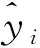
(6)

1.2.1 区域空间权重计算策略

GWR用带宽筛选“有效观测点”进行回归点估计,对于一个给定的回归点X,采样点的权重在该回归点的位置上达到最大,随着两点之间距离的增加,权重逐渐下降。但是这种方式没有考虑空间离散因素。为了更好地刻画空间离散异质性在空间权重计算中的作用,本文提出了区域空间权重计算策略,引入特定因素解释空间离散异质性,对不同空间离散异质区之间的区域影响因子进行分开计算。

受特定因素影响的区域权重的高斯函数rwij定义为

(7)

截尾型核函数为

(8)

式中,rij表示区域影响因子;dij表示观测点i与采样点j之间的距离;h表示带宽。当观测点i和采样点j位于同一区域时,rwij=1,空间核函数的计算与传统GWR没有区别;当观测点i和采样点j位于不同区域时,根据不同空间离散异质区之间的主要差异,计算不同的区域间影响因子rij,如图1所示。

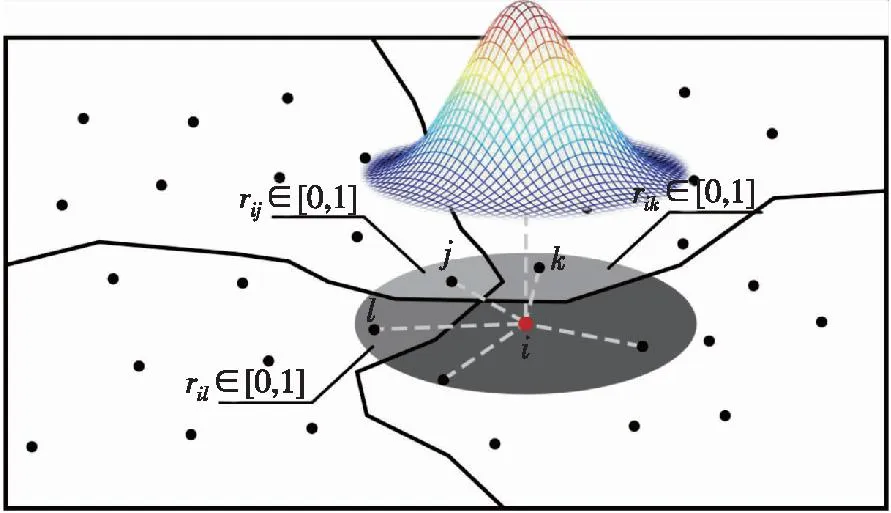
图1 GWR和RGWR高斯核函数空间权重计算策略

1.2.2 区域影响因子的计算方法

(1)一般情况下区域影响因子计算方法。在现实社会中,不同的研究问题和研究区域,影响空间离散异质性的特定因素不同。这需要在建模过程中,针对具体的空间过程和地理现象选定影响空间离散异质性的特定因素,再根据不同区域间主要因素的差异构建不同的影响因子。选定特定因素最简单的方法可以参考混合地理加权回归中直接指定常系数的方式[1,17],直接根据分析师对研究区域和研究对象的经验和前人的研究指定。

例如,本文根据前人研究和对商品房价格研究的经验[21],将研究区内受空间离散异质性影响大的因素划定为研究区域内小学,引入各区重点小学和小学数量,以各区间优质小学教育资源的差异,建立各区受教育影响的区域影响因子为

(9)

式中,rij为区域教育影响因子;ri=qir/qiall;qir为i点所在区域内优质教育资源的数量;qiall为i点所在区域内所有教育资源的数量。

(2)特殊情况下的区域影响因子计算方法。根据式(7)-式(9)区域空间权重的计算存在一种特殊情况:不同空间离散异质区的区域影响因子都相等,rij=固定值。当观测点与回归点位于同一区域时,观测点获得的权重与GWR一致,当回归点和观测点处于不同区域内时,观测点将获得受区域影响因子影响较低的权重。图2(a)为该情况下的固定型带宽策略,图2(b)为调整型带宽策略。

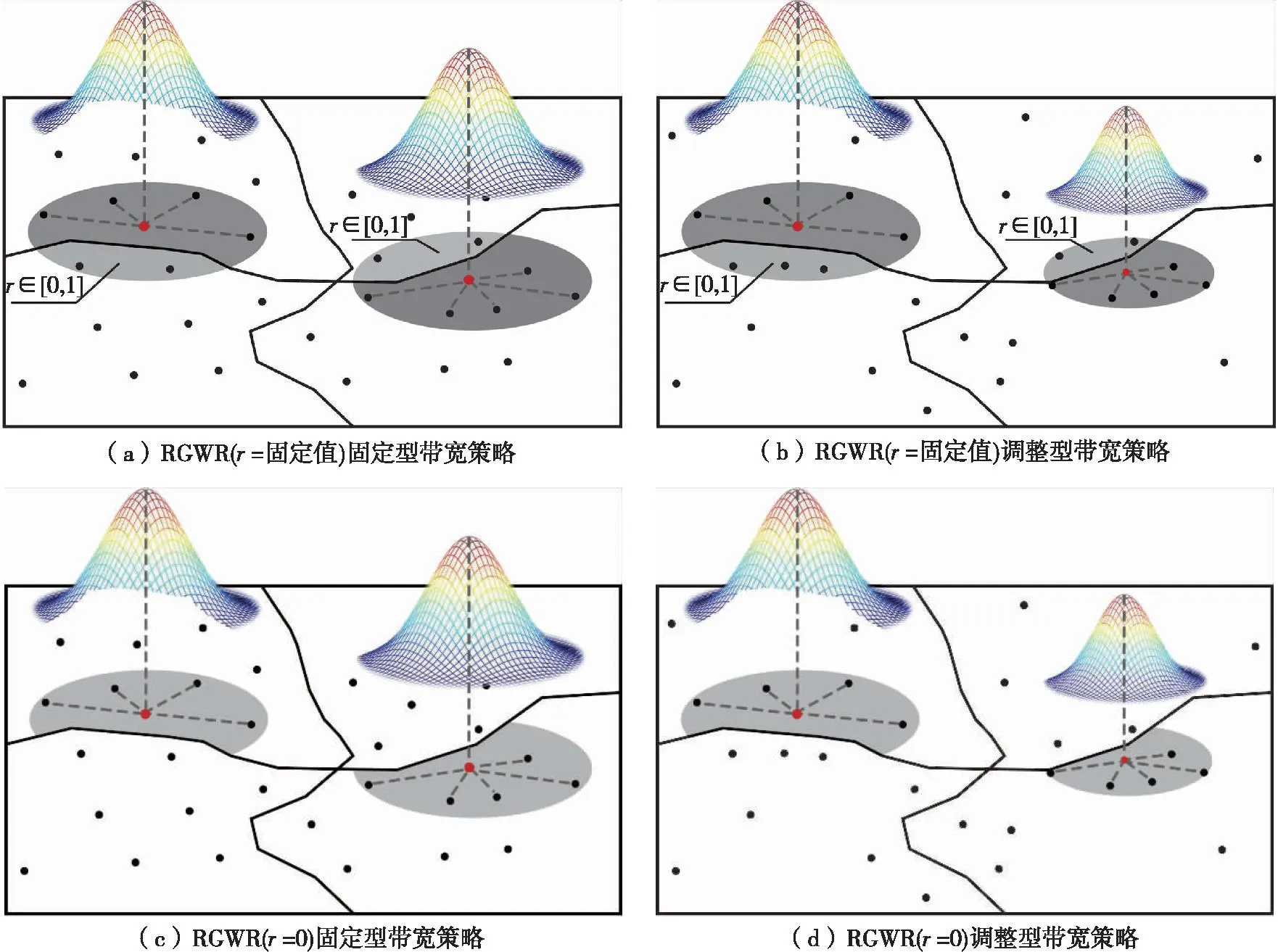
图2 RGWR特殊情况下的高斯核函数空间权重计算策略

当区域影响因子等于0时,此时区域空间权重相当于对不同的空间离散异质区进行了严格的区域判别,即当观测点与回归点位于同一区域时,该观测点将参与回归点的估算;观测点与回归点位于不同区域时,则该观测点不参与回归点的估算。图2(c)为该情况下的固定型带宽策略,图2(d)为对应调整型带宽策略。

由于特殊情况下区域影响因子rij=固定值,估算此情况下的区域影响因子可以参照GTWR估算时间因子的方法,先采用传统GWR方法,按照Akaike信息量准则(Akaike information criterion,AIC)或交叉验证方法(cross-validation, CV),选择最优带宽h,再采用RGWR方法,继续按照AIC或CV方法,最终确定区域因子的取值。

2 算法流程

图3为RGWR模型的算法流程。整体上RGWR估算分为两部分:一是参数调优,即计算最优带宽和区域影响因子;二是参数估计,即估算回归系数、拟合值和模型评价指标。为了方便对区域影响因子的有效性进行比较,对采用特殊情况下的空间权重计算策略的区域地理加权回归记为RGWR-S,其他情况下的区域地理加权回归记为RGWR。

图3 RGWR模型算法流程

数据包括自变量、因变量、空间位置变量、备选带宽和区域影响因子。步骤流程如下:

(1)初始化数据。设置带宽取值范围,针对每个带宽建立GWR模型,对每个观测点构建空间核函数和空间权重矩阵,计算本组带宽对应模型的AIC或CV值,循环上述过程,选择最小AIC或CV值对应模型的参数,即为最优带宽。

(2)设置区域影响因子取值范围,针对每个区域影响因子采用最优带宽建立RGWR-S模型,构建特殊情况下的区域地理加权空间核函数和空间权重矩阵,计算本组区域影响因子对应模型的AIC或CV值,循环上述过程,选择最小AIC或CV值对应模型的参数,即为最优区域影响因子。

(3)利用最优带宽建立GWR模型,对每个观测点构建空间核函数和空间权重矩阵,并计算模型回归系数、拟合值和评价指标。

(4)利用自变量、因变量、空间位置变量、最优带宽和最优区域影响因子建立RGWR-S模型,对每个观测点构建区域空间核函数和区域空间权重矩阵,并计算模型回归系数、拟合值和评价指标。

(5)利用最优带宽建立RGWR模型,构建空间核函数,在每个点i和点j之间建立受特定因素影响的区域影响因子。对每个观测点,计算受特定因素影响的地理加权空间权重矩阵,并计算模型回归系数、拟合值和评价指标。

3 试验及结果分析

3.1 研究区和数据预处理

以武汉市住宅挂牌销售价格为特征价格数据,区域划分以武汉市区级行政区划为标准,构建特征价格模型,开展试验分析。收集了武汉城区957个小区作为样本点,获取各小区2019年12月住宅平均挂牌价格(元/m2)、容积率、绿化率、物业费(元/m2)和建造时间(以1988年为基准年,每增加一年建造时间加1)等属性数据,同时采集了武汉市地铁站、小学、中学等兴趣点数据,见表1。

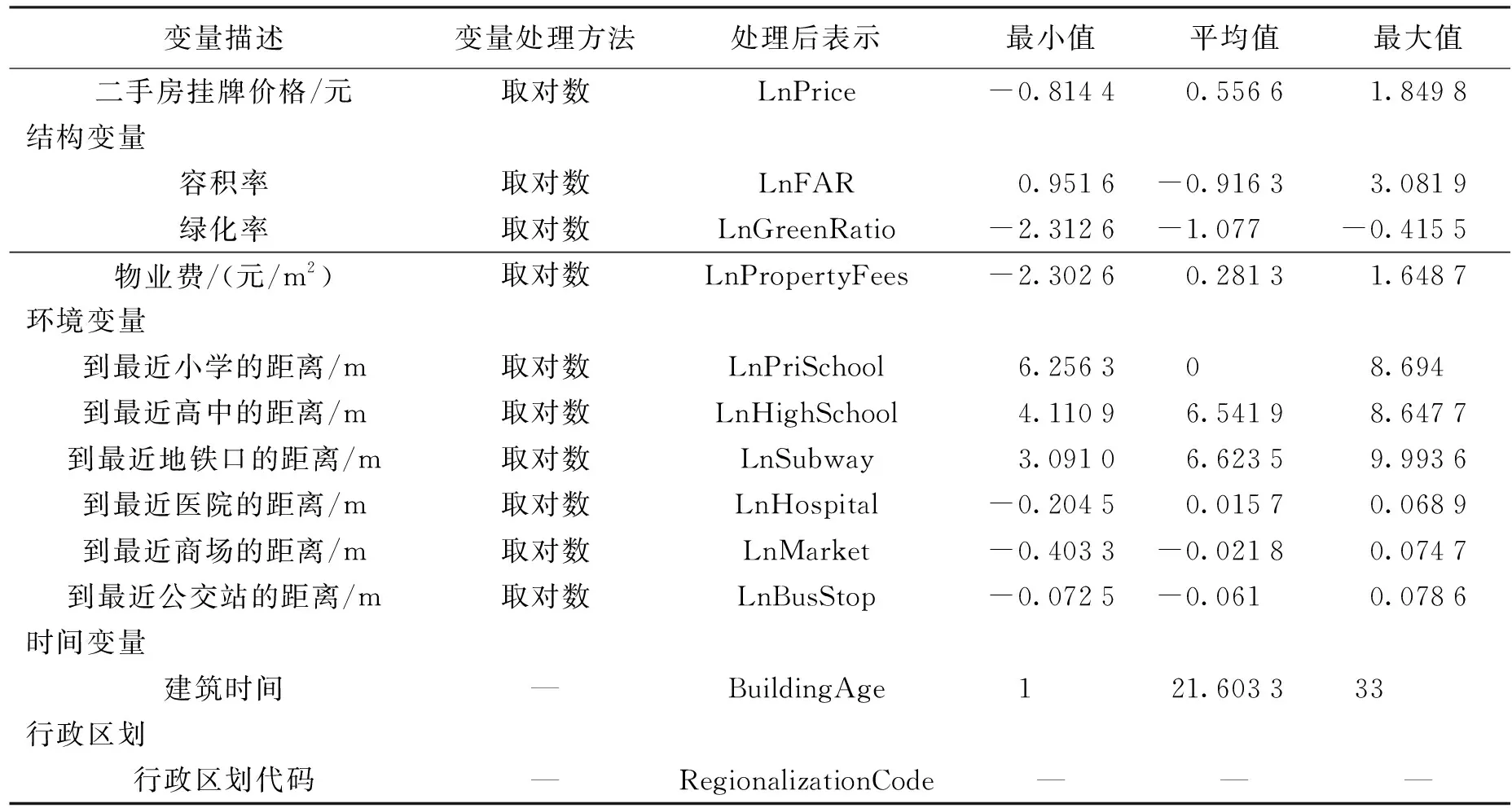
表1 特征价格变量

表2 RGWR和GWR方法性能对比

在建立模型之前,需要对数据进行预处理:首先,计算样本点到最近不同兴趣点的距离,单位均为m;其次,采用叠置分析获取样本点与武汉市各区的区划关系;然后,为了减小量纲和异方差带来的影响,对连续型变量取对数运算[22];最后,采用多重共线性分析和逐步回归分析,确定自变量因素[23]。经计算选取容积率、绿化率、物业费、建造时间,以及小区中心点到最近地铁口、医院、商场、公园、小学和大学的距离作为自变量,小区住宅平均房价为因变量,分别采用GWR、RGWR和RGWR-S方法建立特征价格模型。采用AIC法确定GWR最优带宽,其中最优带宽固定型为12 000,调整型为355。试验以GWR为对比方法,从区域影响因子有效性、模型性能、拟合效果3个角度进行分析。

3.2 试验分析

3.2.1 区域影响因子有效性分析

为了观察区域影响因子对RGWR的影响,令区域影响因子在特殊情况下分别取0,0.05,0.1,…,1,采用基于高斯核函数的RGWR,分别计算基于固定型带宽和调整型带宽下各模型的拟合优度(R2)、均方根误差(root mean squared error, RMSE)和误差项平方和(sum of squares for error,SSE)。结果显示,首先,两种带宽策略下各模型的R2均大于0.6,说明采用RGWR方法可以建立可靠的特征价格模型,较好地估算武汉城区住宅销售价格;然后,两种带宽策略下,R2随着区域影响因子的增大而减小,RMSE和SSE随着影响因子的增大而增大,当r=1时(即GWR),R2最小,RMSE和SSE最大,模型性能最差,当r不等于1时,R2、RMSE和SSE均有提升,证明区域因素存在且影响拟合精度,考虑区域因素影响后,模型精度有所提升;最后,图4(a)显示在固定型带宽策略下,当r=0时,R2最大,RMSE和SSE最小,模型拟合效果最好,图4(b)显示在调整型带宽策略下,当r=0.05时,R2最大,RMSE和SSE最小,模型拟合效果最好。说明区域影响因子越小,武汉城区住宅销售价格特征模型精度越高。考虑区域因素后,模型精度均有大幅度提升,说明区域影响因子对于改进地理加权回归方法有显著作用。

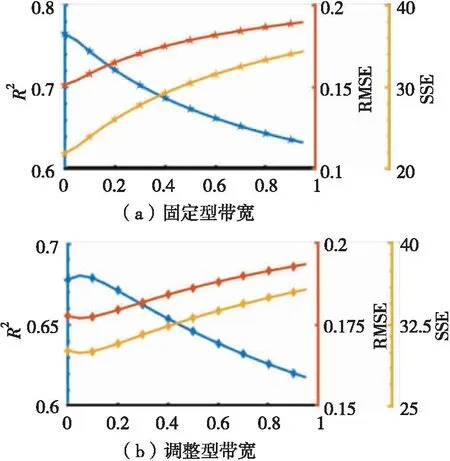
图4 RGWR模型精度随区域影响因子的变化趋势

3.2.2 模型性能对比

由图4可知,特殊情况下,在固定型带宽策略下r=0时,RGWR模型拟合效果最好;在调整型带宽下r=0.05时,RGWR模型效果最好。表1为RGWR模型、RGWR-S与GWR的相关指标对比情况。RGWR模型在固定型带宽下,R2为0.766 2,比GWR模型提升了21.83%,调整R2(R2adj)提升了22.23%,MSE提升了37.09%,RMSE提升了20.64%,SSE提升了37.01%。RGWR模型AIC值为-319.122 4,比GWR小11.782 4。RGWR在调整型带宽下,GWR模型和区划因子r=0.05时的RGWR-S模型提升效果不如RGWR模型,此时RGWR模型R2为0.680 4,比GWR模型提升了10.58%,R2adj提升了10.75%,MSE提升了16.93%,RMSE提升了8.85%,SSE提升了16.91%。一般地,AIC相差3以上说明两个模型有显著差别,AIC值越小,模型拟合精度越高[24]。说明不论是固定型带宽策略还是调整型带宽策略,RGWR均能够比GWR更好地模拟武汉城区住宅销售价格。

3.2.3 模型拟合效果比较

通过比较RGWR和GWR模型中房价的预测值和实际值,可以直观地探索模型的拟合效果。在前文中,已能够说明在本文研究区域,无论是固定型还是调整型带宽策略,RGWR模型估算效果最好,因此采用RGWR的拟合效果分布与两种带宽策略下的GWR模型进行对比。图5为固定和调整型带宽策略下RGWR和GWR的拟合效果分布,虚线表示实际值与预测值相同。因此,预测值点分布和真实值点位置越接近虚线,模型的拟合效果越好。

图5 不同模型拟合散点

在相同的带宽策略下,RGWR的点分布在虚线附近,显著高于GWR的点分布,表明RGWR模型的拟合效果比GWR的拟合效果显著提高。类似的,在固定带宽策略和自适应带宽策略之间,可以看到RGWR固定带宽的点分布高于虚线附近的自适应带宽。同时,固定带宽策略下RGWR模型的R2值为0.777 7,比自适应带宽下的R2值高18.64%。这表明,在本文的数据环境中,固定带宽策略下RGWR模型的拟合效果优于自适应带宽策略下的RGWR模型。

4 结 语

本文提出了一种区域地理加权回归方法,通过构建区域空间权重计算策略,在空间核函数计算中引入区域影响因子变量,修正空间核函数,优化空间权重,在探测空间非平稳性的同时探测空间离散异质性。最后以武汉市住房销售价格为例开展试验分析,证明了引入区域影响因子的有效性。研究发现,在武汉市住房销售价格模型中,模型精度随着区域影响因子的减小而增大,说明区域影响因子对于改进地理加权回归方法有显著作用。同时,当采用受教育影响区域影响因子时,模型的拟合效果好于采用固定值的方式,RGWR方法相比传统的GWR方法R2提升了21.83%,说明RGWR能够有效解决空间离散异质的区域对武汉市住房销售价格影响的问题。

本文提出的“区域”并不只是行政区划,在面对不同的研究问题时,可以根据不同的特征选择不同的分区方式和分区尺度,如可以按照行政区划、流域、温度带、经济圈等方式对区域进行分区。后续研究将着力于如何进一步优化算法提高拟合精度,以及将该方法应用于不同分区尺度、不同领域的不同分区方式的适用性和差异性。