基于状态空间模型的加工中心功能铣头实时寿命预测

刘丽娜，秦飞跃，2，宋欣钢

(1.黄河交通学院机电工程学院，河南焦作 454950；2.河南理工大学机械与动力工程学院，河南焦作 454003)

0 前言

数控机床是目前最为热门的加工设备，而铣头是数控机床中最重要的设备之一。铣头加工成本较高、生产周期较长，因此在有限的环境和运行数据下，建立铣头的寿命预测模型具有重要的研究意义[1]。铣头在运行过程中因关键零部件磨损、结构问题以及本身质量问题，导致加工精度下降，进而使得铣头失效[2-3]。当铣头出现一定的磨损之后，最直接的表现就是温度不断上升，因此可以通过测定运行过程中的温升数据判断铣头的运行状态[4]。彭卫文等[5]使用运行过程中的温升数据，应用贝叶斯方法，结合故障机制构建加速性能退化实验，建立了铣头的可靠性评估预测模型。刘毅[6]分析了直角铣头的常见故障，发现直角铣头故障一般都是由台阶、螺旋伞齿轮齿面以及轴承磨损、壳体破坏等构成，故障的主要原因还是铣头内部磨损。但是，目前有关铣头的寿命预测模型研究相对较少，再者铣头的寿命预测数据相对难以获取，许多研究学者目前主要采用可靠性研究方法对数控机床及其关键零部件进行寿命预测[7-8]。

铣头运行过程中的温度升高是其内部磨损、性能退化的直接体现。实际生产过程中，铣头的退化状态不可直接测量，本文作者提出基于状态空间模型对铣头运行过程中的退化状态进行描述，并使用贝叶斯状态估计对建立的模型进行求解，计算铣头的失效时间分布，实现对铣头实时寿命的预测[9]。

1 模型建立

在设备或者系统运行过程中，会呈现出两种状态变量：一种是可以直接通过相应的传感器测量到的数据，这种状态变量称为观测量，也可称为可观测序列；另外一种是无法通过相应的传感器测量，但是却真实存在的变量，这种状态变量称为状态向量。状态向量能真实反映出设备或者系统运行的内在运行状态，它由一个马尔科夫链构成。状态空间模型建立了可观测量与状态向量之间的关系，通过状态空间模型，能将设备或者系统运行过程中的内在状态呈现出来。

图1描述了系统或者设备运行过程中可观测量与状态向量之间的关系，其中A0，A1，…，An，An+1指的是系统或者设备运行过程中的状态向量，与之对应的B0，B1，…，Bn，Bn+1是系统或者设备的可观测序列。

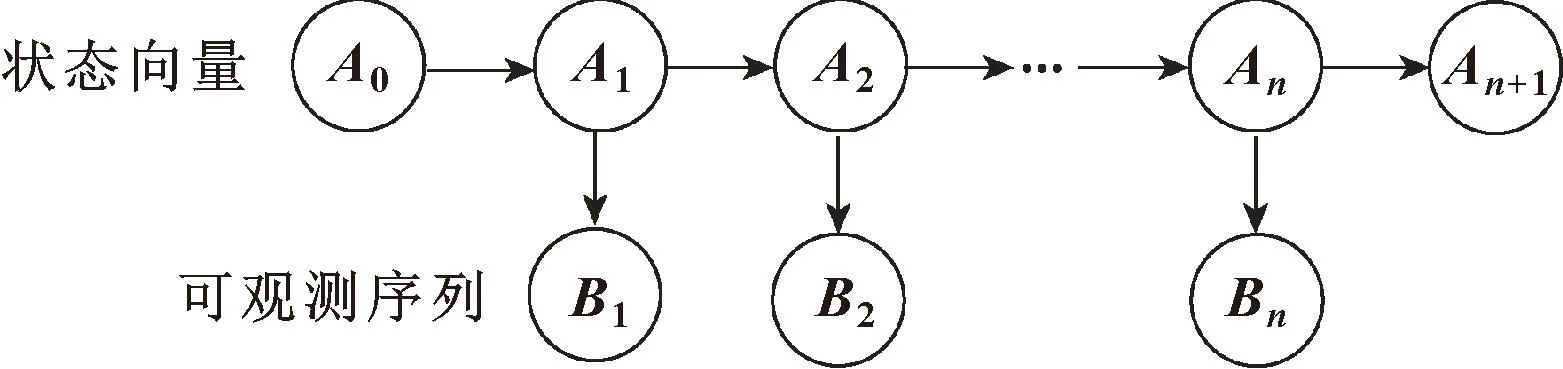
图1 状态向量与可观测序列之间的关系Fig.1 Relationship between state vector and observable sequence

贝叶斯状态估计与预测可以用来对状态空间模型求解。每当传感器观测到一个数据时，可以得到一个先验分布，通过贝叶斯公式计算得到一个后验分布。当观测到新数据时，之前产生的后验分布可以作为先验分布，继续参与计算得到新的后验分布，如此循环往复，每当观测到新的数据，就可以及时更新模型参数，从而实现对设备或者系统的状态估计。

铣头作为一种复杂的精密机械设备，随着运行时间的增加，会因为关键零部件磨损而使得加工精度降低，而关键的零部件磨损无法通过相应的传感器测量出来，最终表现出来的是铣头温度增加，因此可以通过测量温度，利用建立的状态空间模型实现对铣头的寿命预测。

铣头性能退化及实时寿命的状态空间模型可以通过式(1)来实现[10]：

(1)

其中：gθ(·)为状态方程，描述铣头退化状态随着运行时间的变化关系；fθ(·)为观测方程，指铣头在运行过程中温度与其内部的关系；t为铣头的运行时间；yt为铣头运行到t时刻的可观测序列，即温度；xt为铣头运行到t时刻的实际退化状态；wt和vt分别为系统的过程噪声和观测噪声。

已知t时刻的铣头状态后验分布π(xt|y1，t)，根据贝叶斯公式，可得到任意t+k的状态分布：

π(xt+k|y1,n)=

(2)

累积失效概率指设备或者系统运行期间内的失效概率。假设文中研究对象铣头设定的温度阈值为TR，当铣头运行过程中温度Tr超过设定的阈值时，即可判定铣头失效。设F(t)为铣头运行t时刻后的累积失效概率，累积失效概率计算公式[11]为

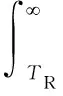
(3)

利用式(2)得到t+k时刻的状态分布后，根据式(3)可以得到t+k时刻的铣头累积失效概率为

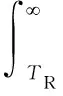
(4)

失效概率密度是对累积失效概率公式的微分，铣头在t时刻的失效概率密度的表达式为

本次研究纳入的4100例孕妇中共计有26例经产后或者引产证实为胎儿肢体缺陷。产前常规超声检出12例，联合检查检出17例，连续顺序追踪超声检出25例。连续顺序追踪超声检出效果明显优于其他超声检查，P＜0.05，差异具有统计学意义，见表1。

(5)

给定铣头的温度后，以动态线性增长模型作为状态方程，描述铣头的退化轨迹[12]，如式(6)所示：

(6)

使用R语言对建立的铣头性能退化模型进行编程并求解[13]，可以得到任意时刻陶瓷铣头的性能退化状态、累积失效概率以及失效概率密度。

任何预测模型得出的结果与真实值都有一定的偏差，在预测过程中也有一定的不确定性，为了消除此种不确定性带来的影响，在预测模型中引入置信区间来增加预测结果的可靠性，文中将置信区间设置为95%。

2 结果与分析

2.1 铣头退化状态估计与预测

由于寿命数据具有难以获取、样本小以及成本高等特点，因此文中使用的铣头在运行过程中的温度数据及其获取方法见文献[5]。图2所示为铣头运行过程中的温升数据。

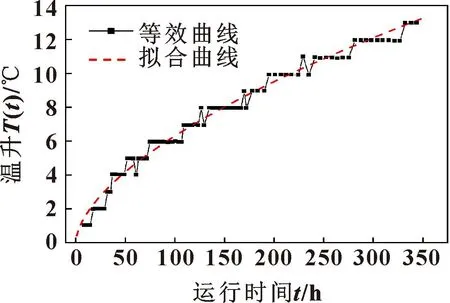
图2 铣头温升数据Fig.2 Milling head temperature rise data

通过对铣头温升的数据进行最小二乘拟合，可以得到铣头寿命公式如式(7)所示：

T(t)=0.408 8×t0.593 9

(7)

其中：t为铣头实际运行时间，h；T(t)为铣头温升，℃。

假设当温升达到13 ℃时，铣头寿命结束。通过式(7)计算此时铣头理论运行时间为338.6 h。

图3所示为基于铣头运行前110 h的温升数据得到的铣头预测运行时间。通过上述建立的状态空间模型计算出铣头温升为13 ℃时所需要的运行时间为191.8 h，与通过式(7)计算出的理论运行时间338.6 h差别较大。铣头运行前110 h时退化状态变化率δ110=0.023。图中阴影面积为根据式(3)(4)、使用前110 h的温升数据计算得到的运行第220 h时铣头的累积失效概率。此时的阴影面积较小，说明铣头在较短的运行时间时，失效概率较低，铣头可靠度较高。

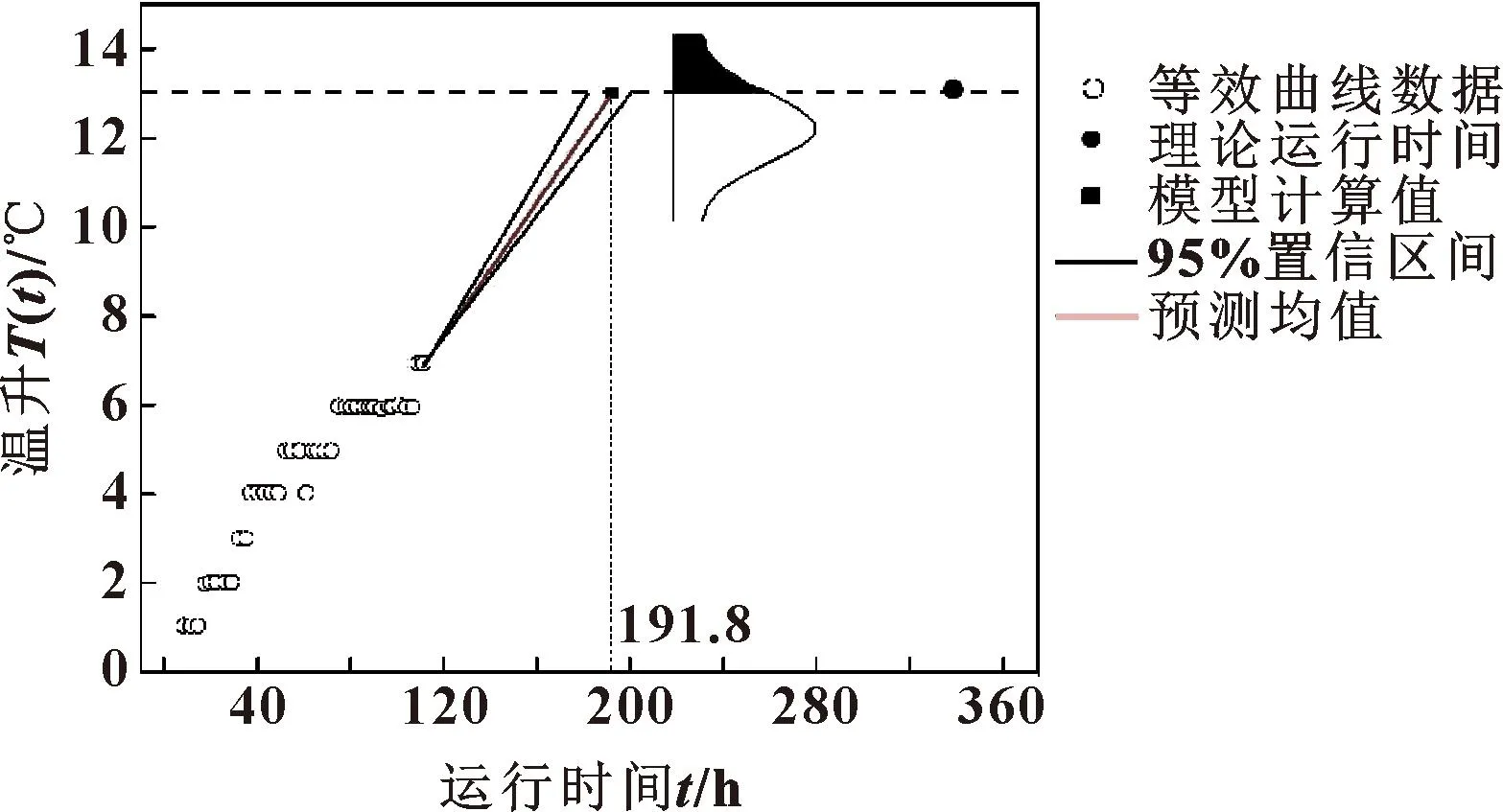
图3 基于运行前110 h铣头温升数据的退化状态估计与预测Fig.3 Degradation state estimation and prediction based on the first 110 h milling head temperature rise data

图4所示为基于铣头运行前220 h的温升数据得到的铣头预测运行时间。通过状态空间模型计算出铣头温升为13 ℃时所需要的运行时间为275.3 h，与通过式(7)计算出的理论运行时间338.6 h还是有一定的差别，但是与运行前110 h温升数据相比，差别进一步缩小。铣头运行前220 h时退化状态变化率δ110=0.015，退化状态变化率与运行前110 h相比，进一步减小。图中阴影面积为根据式(3)(4)、使用前220 h的温升数据计算得到的运行第310 h时铣头的累积失效概率。此时与前110 h温升数据对比，阴影面积增大，说明铣头在又运行了110 h后，失效概率增大，可靠度降低。

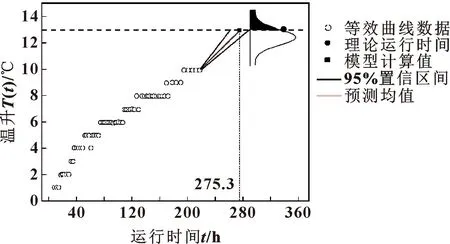
图4 基于运行前220 h铣头温升数据的退化状态估计与预测Fig.4 Degradation state estimation and prediction based on the first 220 h milling head temperature rise data

图5所示为基于铣头运行前310 h的温升数据得到的铣头预测运行时间。通过状态空间模型计算出铣头温升为13 ℃时所需要的运行时间为330.5 h，与式(7)计算出的理论运行时间338.6 h差别进一步缩小。可以看出：在置信区间内，失效时间预测已经超过理论运行时间，证明预测模型的准确性。由于失效时间预测已经超过理论运行时间，因此再对运行338.6 h后铣头的累积失效概率计算已经没有实际意义，这里不再给出累积失效概率预测图。铣头运行前310 h时退化状态变化率δ110=0.008，其退化状态变化率进一步减小，这也能与图2铣头温升数据前期增加较快、后期增加较慢相印证。

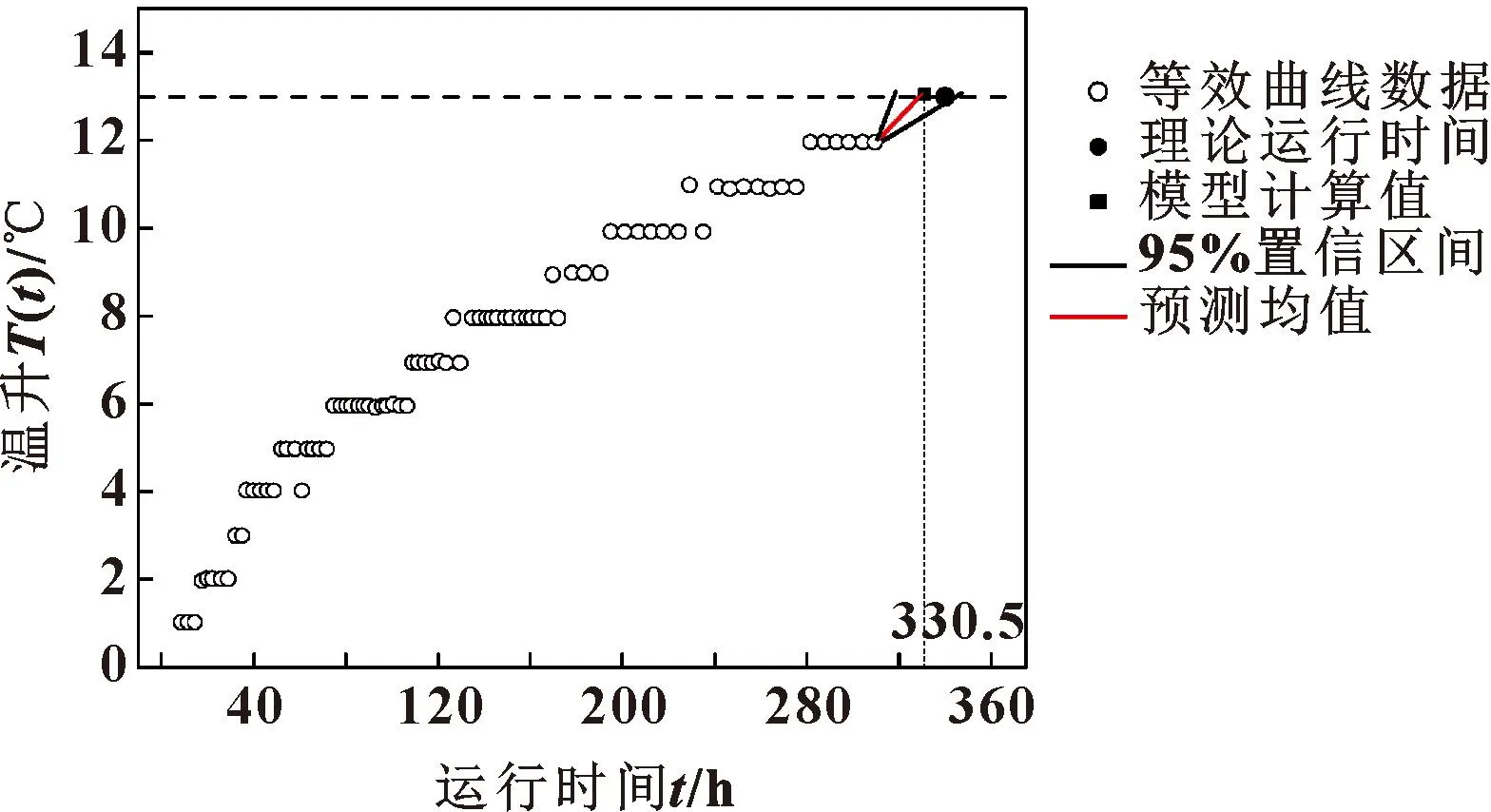
图5 基于运行前310 h铣头温升数据的退化状态估计与预测Fig.5 Degradation state estimation and prediction based on the first 310 h milling head temperature rise data

2.2 铣头失效概率密度预测

结合式(4)(5)计算可以得到任意时刻铣头的失效概率密度分布。文中分别选取铣头运行前110、220、310 h时的温升数据，计算对应的失效概率密度分布，如图6所示。其中竖直垂线是铣头温升阈值为13 ℃时，由式(7)计算得到的理论运行时间，为338.6 h。

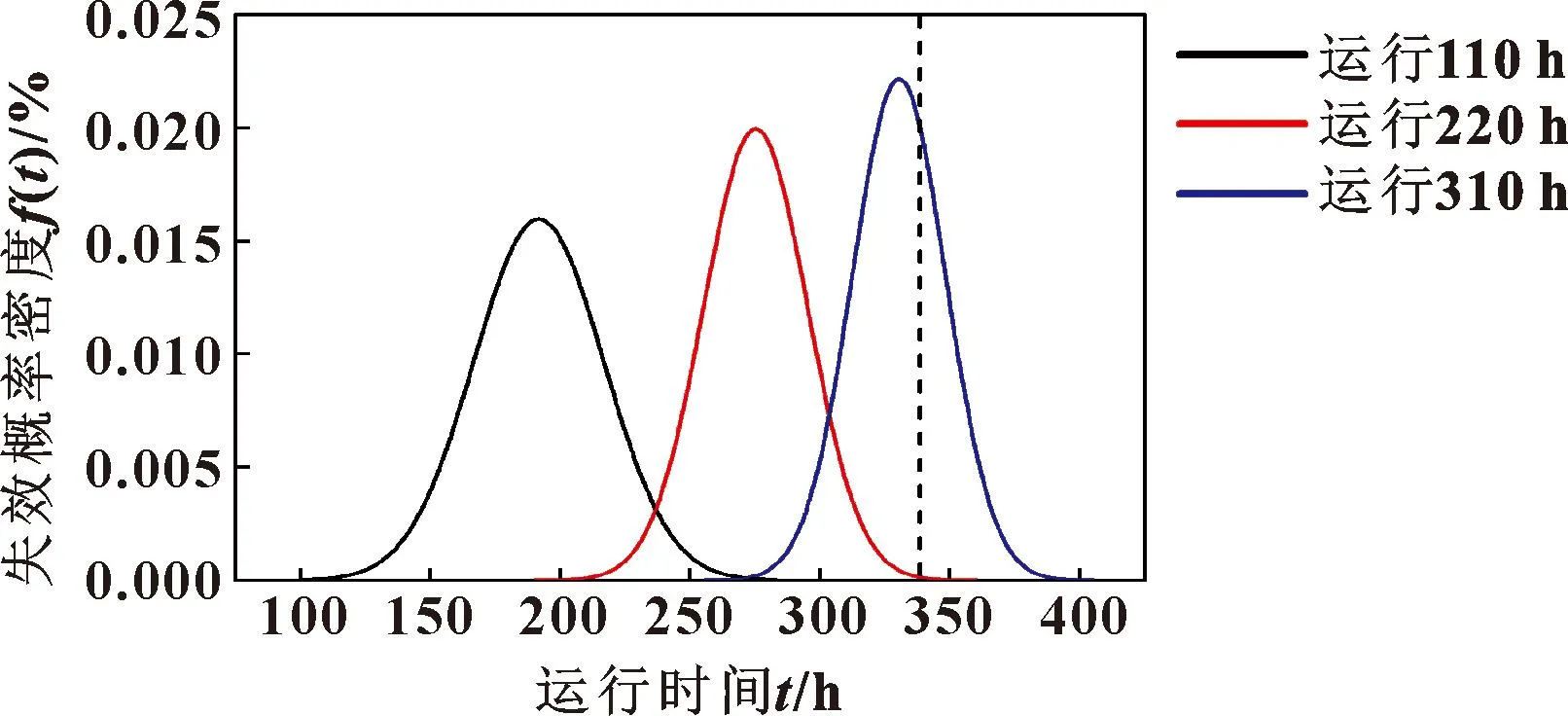
图6 铣头失效概率密度预测Fig.6 Failure-probability density prediction of milling head

由图6可以看出：随着温升数据不断增多，铣头失效时间预测越来越收敛于理论值，说明模型预测的不确定性越来越小。这是因为贝叶斯能不断融入新的温升数据，通过计算先验分布和后验分布来及时更新状态空间模型参数。

3 结论

铣头在运行过程中，由于关键零部件磨损使得加工精度降低，从而导致其性能状态不断退化，而且退化状态不可直接测量，只能通过测定运行过程中铣头温升来判断退化状态；同时铣头寿命数据具有难获取、样本小以及成本高等特点，使得难以实时预测铣头寿命。文中以实际运行过程中铣头温升数据为基础，结合状态空间模型与贝叶斯理论，建立了铣头的实时寿命预测模型。得到的结论如下：

(1)建立的铣头实时寿命预测模型可以根据前期铣头的温升数据，来预测任意时刻铣头退化状态以及剩余寿命，并且可以根据最新融合的温升数据及时更新模型参数，从而使得预测结果越来越收敛于理论值。

(2)随着运行时间的增加，预测模型计算得到的铣头退化状态变化率逐渐减小，这与铣头刚开始投入使用时温升增加较快、后期增加较慢这一现象相互印证。

(3)不同运行时间内，模型计算出的铣头失效概率密度随运行时间的增加不断接近真实值，一定程度上可以为铣头失效做出判断。