基于多信息融合与GRU的轴承剩余寿命预测

2024-01-16曹胜博徐彦伟颉潭成王浏洋

机床与液压 2023年24期

曹胜博，徐彦伟，2，颉潭成，2，王浏洋

(1.河南科技大学机电工程学院，河南洛阳 471003；2.智能数控装备河南省工程实验室，河南洛阳 471003)

0 前言

地铁牵引电机轴承作为整个地铁动力系统的关键零件，其性能的好坏直接影响地铁动力系统能否正常运行。在实际工作中，地铁需要频繁地启动停止，地铁牵引电机轴承需要频繁承受载荷和转速的变化，使得轴承容易产生内外圈裂纹、滚动体点蚀等故障[1]。牵引电机轴承一旦出现故障，极易造成重大经济损失及人员伤亡。如果使用一定的方法计算出地铁牵引电机的剩余寿命，及时发现早期故障并对设备进行维护，地铁发生重大事故的风险将大大降低。

传统的滚动轴承剩余寿命预测方法主要通过模拟机制构建数学模型进行[2]。但在实际应用中，轴承的工作环境复杂，退化过程具有随机性，难以建立准确的机制模型。基于数据驱动的寿命方法不需要建立繁杂的数学机制模型，并且能够有效利用各种算法挖掘数据中的隐藏特征，建立轴承的性能退化模型，预测轴承寿命，逐渐成为研究的热点[3-5]。随着计算机技术的不断发展，越来越多的研究人员使用深度学习技术建立轴承退化模型，进行轴承寿命预测方面的研究[6]。在采集轴承的振动信号时，往往包含其他零部件间的噪声。如何对采集到的信号进行处理，是轴承剩余寿命预测的重中之重。唐旭等人[7]从多元时间序列中提取时域特征数据导入神经网络，进行剩余寿命预测。赵德尊等[8]研究了基于自适应广义解调变换的滚动轴承时变非平稳故障特征的提取方法。卷积神经网络作为深度学习中一种常用的网络模型，常被用于挖掘数据的深度特征。杨宇等人[9]提出一种动态自学习深度置信网络，可以从原始信号中提取退化特征，不但缩短训练神经网络的时间，同时提高了模型预测准确度。王玉静等[10]使用一维卷积神经网络直接对原始一维振动信号进行特征提取。周扬将采集到的未经处理的一维振动信号转化为二维灰度图，之后将灰度图导入卷积神经网络中进行故障识别，取得了良好的效果[10]。

在寿命预测方面，深度学习技术也展现了强大的非线性拟合能力。张世岩等[11]提出一种结合时间序列数据扩增和双向长短时神经网络的轴承寿命预测方法，通过对采集到的时间序列数据进行扩增，分析轴承实际工作过程中的退化规律，旨在提高轴承寿命预测的精度。臧传涛等[12]在长短时记忆神经网络的基础上，使用黏菌算法优化参数，取得了良好的预测效果。

上述方法大多只采集单一振动信号作为数据处理的素材，而振动信号在实际采集过程中极易受到轴承工作环境的干扰。为解决这一问题，本文作者提出一种基于信息融合的门控单元神经网络预测模型。该模型使用声发射信号和振动信号融合后的信号作为输入，能有效弥补单通道数据易受干扰的不足，然后使用GRU神经网络对寿命进行预测。

1 相关理论

1.1 一维卷积神经网络

卷积神经网络根据输入维度的不同可以分为：一维卷积、二维卷积、三维卷积等。其中提取一维信号数据时，一维卷积神经网络在特征提取时表现出良好的效果。单层的卷积神经网络由2个主要部分组成：卷积层和池化层。CNN提取特征的主要步骤为：(1)输入的一维数据被卷积核依次遍历，挖掘出深度特征信息；(2)池化层对这些信息进行压缩降维，选取其中更具有代表性的数据；(3)进行过卷积，池化后产生的新数据序列作为输入，进行下一次卷积和池化，直到得到想要的数据。下面是具体的运算过程。

(1)卷积层。卷积层的任务是提取出数据中包含的退化信息。根据设计的卷积核的大小，得到不同的特征值。其具体步骤为：卷积核在一维数据上扫描，每移动到一个新的位置，便对该位置的数据进行加权求和，依次进行，直到遍历完整个数据。提取的数据长度受到卷积核的影响。可以通过设置卷积核的个数、大小、步长等参数调整提取出的特征值。卷积的计算公式如下：

(1)

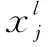
(2)池化层。由于卷积得到的数据量大，含有冗余，因此需要输入池化层中进行降维处理。池化操作可以有效降低计算量，并减少模型过拟合的概率。池化函数有多种选择，例如平均池化、L2-范数池化、最大值池化等。其计算公式如下：

(2)

1.2 GRU神经网络

传统RNN方法在处理长序列数据时，随着数据量的不断增加，因为网络结构的原因，会因数据长期依赖带来梯度消失和梯度爆炸等问题，影响最终的预测效果。为解决这些问题，GRU和LSTM神经网络随之而生。这两者都通过引入一组储存单元，使得神经网络可以自主学习，保存重要历史信息，及时更新储单元[13]。两者不同的是，GRU的网络结构将LSTM网络的输入门和遗忘门合二为一成为更新门。GRU的具体结构如图1所示。

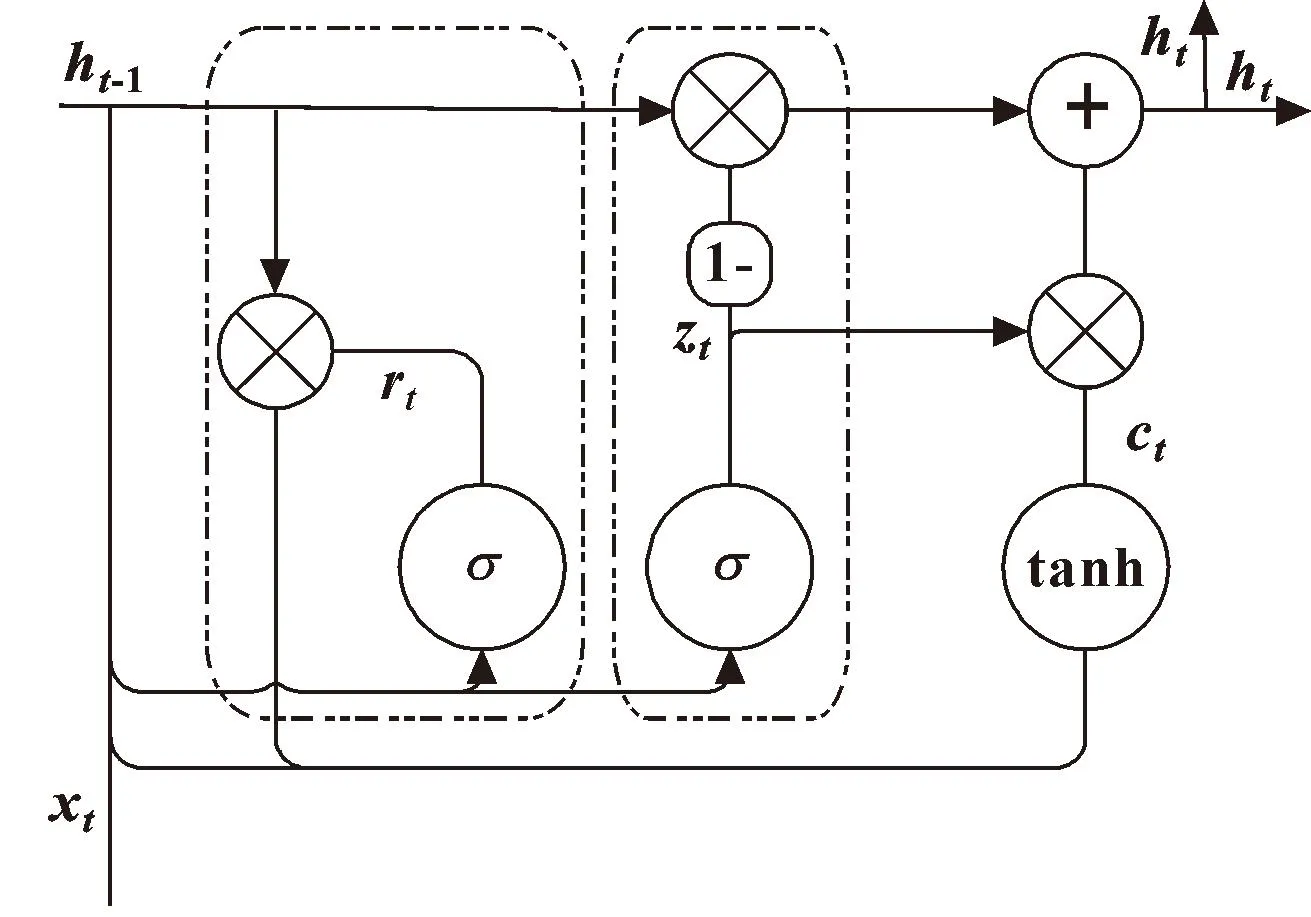
图1 GRU网络结构Fig.1 GRU network structure

图中，zt为更新门，rt为重置门。其中更新门的作用是调整前一时刻状态ht-1对当前状态ht的影响量。前一状态对当前状态的影响越大，更新门的数据值越高，数据传入的信息越多。其表达式如式(3)所示：

zt=σ(wxz+xt+whzht-1+bz)

(3)

重置门的作用是控制前一时刻的状态ht-1对候选状态ct的影响量。前一状态对候选状态的影响越小，重置门的数据值越低，数据传入的信息越少。

重置门的表达式和更新门表达式相同，只是线性变换的参数和偏置有所改变，计算方法见式(4)：

rt=σ(wxrxt+whrht-1+br)

(4)

最后，可得候选状态ct和输出ht为

ct=tanh(wxcxt+whc(rt⊗ht-1)+bc)

(5)

ht=(1-zt)⊗ht-1+zt⊗ct

(6)

式中：xt为输入序列；ht-1为上一时刻隐藏状态；ht为当前隐藏状态；wxz和whz是更新门的权重矩阵；wxr和whr是重置门的权重矩阵；wxc和whc是候选状态的权重矩阵；bz、br、bc表示相应的偏置。图中的⊗表示逐元素相乘，tanh表示tanh函数作为候选状，σ表示Sigmoid函数，其表达式分别如公式(7)和公式(8)所示。

tanh(t)=(et-e-t)/(et+e-t)

(7)

σ(t)=1/(1+e-t)

(8)

设置Sigmoid函数作为更新门和重置门的激活函数，输出值固定在0～1之间，以此达到保留或忘记信息的效果。

1.3 信息融合

由于采集到的振动信号和声发射信号中量纲不统一，需要对特征信息进行信息融合。根据融合方式的不同，信息融合技术可分为决策层融合、数据层融合和特征层融合。决策层融合会对采集的数据进行压缩处理，势必导致信息的大量丢失，不适合处理轴承寿命数据。由于振动传感器和声发射传感器探测技术不同，因此不适合直接将数据合并的数据层融合。特征层融合是先分别提取不同传感器的特征值，之后通过归一化处理消除不同传感器的差别，能够有效保留轴承退化信息。此次试验选用特征层融合[15]，其融合方式如图2所示。

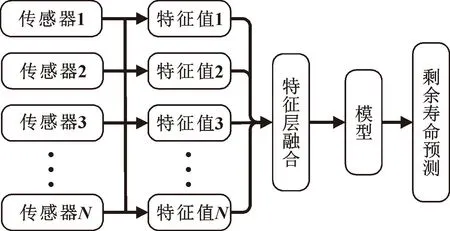
图2 融合方式Fig.2 Fusion method

选择归一化进行特征层融合。一维卷积采集到的信号特征属于离散型数据变量，适合选用线性归一化方法。线性函数常用的归一化方式如公式(9)所示：

(9)

其中：x为经过特征提取后的离散数据；xmin为处理后数据的最小值；xmax为处理后输入数据的最大值；y为最终的输出值。

1.4 轴承寿命预测流程

图3所示为牵引电机轴承寿命预测流程。具体为以下步骤：

图3 轴承寿命预测流程Fig.3 Flow of bearing life prediction

(1)信号采集。使用振动传感器和声发射传感器分别采集轴承的振动信号和声发射信号。

(2)特征提取。对采集到的轴承振动信号和声发射信号进行傅里叶变换(Fast Fourier Transform，FTT)，使用卷积神经网络自动提取出包含退化信息的特征数据。

(3)归一化处理。为减少不同传感器采集数据的物理影响，需要对提取出的振动信号和声发射信号的特征进行归一化处理。

(4)剩余寿命预测。以归一化后的特征参数作为神经网络的输入、轴承的剩余寿命作为标签对CNN-GRU模型就行训练。

2 试验验证

2.1 试验设计及平台

文中使用的地铁牵引电机试验轴承型号为NU216，结构参数如表1所示。

表1 轴承结构尺寸Tab.1 Bearing structure dimensions

为了减少试验周期，同时模拟轴承实际运行中可能产生的早期缺陷，使用大族YLP-MDF-152型三维激光打标机在滚动体上进行缺陷预制，预制的点蚀直径为20 μm，裂纹宽度为15 μm，在此基础上进行剩余寿命试验。

试验按照GB/T 24607-2009《滚动轴承寿命与可靠性试验及评定》标准进行[14]，详见表2。共采集2 000组包含轴承衰退信息的信号。

轴承退化信息采集系统由轴承试验台、试验轴承、传感器采集模块液压加载模块和计算机组成，如图4所示。

图4 轴承试验台Fig.4 Bearing test bench

2.2 轴承寿命预测流程

首先对采集到的振动数据和声发射数据进行傅里叶变换(FTT)，之后使用一维卷积神经网络对特征进行深度提取。

对提取出的特征信息归一化处理后划分训练集测试集。对模型进行训练前要对轴承数据集样本进行寿命标签设置。引入健康度指标(HI)作为标签，其计算公式如式(10)所示：

(10)

式中：T为全部的数据集数量；t为当前的数据集序号；δHI的取值为0～1。数据集序号按照时间序列排序。0点代表轴承完全失效时刻，1点代表轴承退化起始点时刻。最后，双通道数据的CNN-LSTM和单通道数据的CNN-GRU网络进行对比，以验证模型的有效性。

文中设计的网络模型由特征提取层和分类层组成，具体设计为卷积-卷积-池化-卷积-卷积-池化-卷积-卷积-池化-卷积-卷积-池化-全连接-GRU分类器的结构模型。其中，池化层采用最大池化方式。模型参数如表3所示。

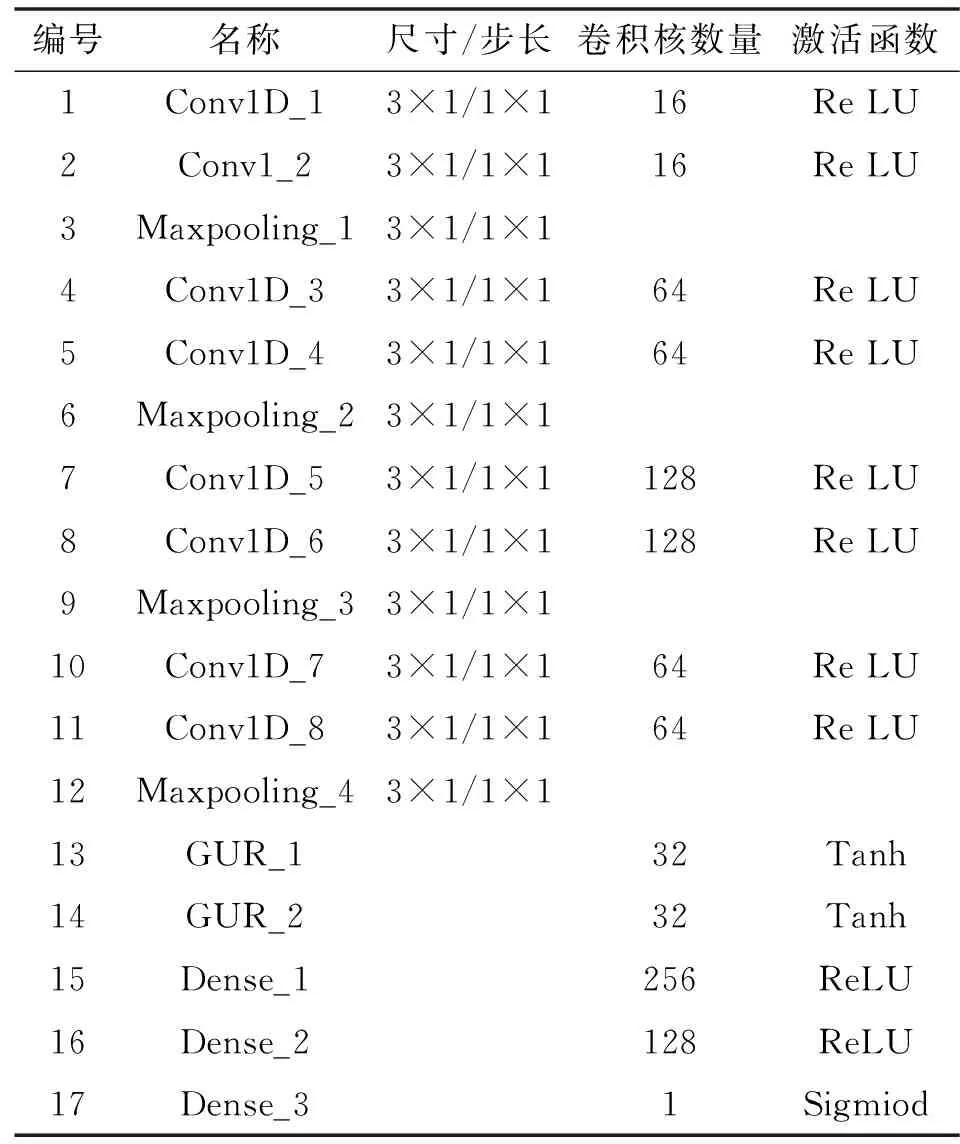
表3 模型结构与参数配置Tab.3 Model structure and parameter configuration

将归一化后的特征数据输入GRU网络进行训练，同时将均方误差函数作为损失函数，并采用Adam优化器对网络权值进行更新。将测试集的退化特征向量输入到训练好的GRU模型当中，输出得到测试集轴承的剩余寿命。

由图5可以看出：当迭代次数达到30次左右时，模型的损失函数已经稳定。图6所示为预测效果。可以看出：经过双通道数据训练的CNN-GRU模型的拟合效果良好。

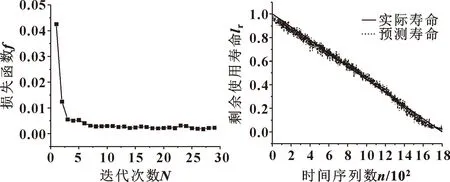
图5 损失函数曲线图6 双通道CNN-GRUFig.5 Curve of loss function Fig.6 Dual channel CNN-GRU

为了达到对比效果，单振动信号输入的CNN-GRU模型和双通道输入的CNN-LSTM模型使用同一数据进行寿命预测。效果如图7、8所示。为了进一步说明模型的预测效果，用均方根误差(Root Mean Square Error，RMSE)为指标进行评估，均方根计算公式如式(11)所示。计算结果见表4。

表4 预测误差Tab.4 Prediction errors

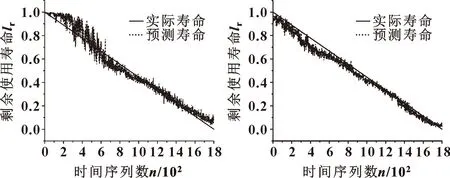
图7 单通道CNN-GRU 图8 双通道CNN-LSTMFig.7 Single channel CNN-GRU Fig.8 Dual channel CNN-LSTM

(11)

式中：m为数据数量；y(i)为模型输出的预测值；x(i)为采集到的真实值。

由图7、8和表4可知：(1)双通道CNN-GRU模型相较于单通道的CNN-GRU模型预测误差更低，说明采用信息融合技术的双通道预测模型能够有效提高预测精度。(2)双通道CNN-GRU模型相较于双通道的CNN-LSTM模型预测误差更低，说明最后的预测算法选择结构更简便的GRU模型比LSTM模型效果更好。