GA-LSTM模型在数控机床故障预测中的应用

王舒玮，薛敏杰

(1.山西大同大学机电工程学院，山西大同 037000；2.内蒙古北方重工业集团有限公司试验基地，内蒙古包头 010400)

0 前言

数控机床是最典型的机电设备，其主要特点是灵活性好、效率高、精度高、产品质量稳定。数控机床涵盖自动控制技术、机械制造技术、计算机技术和测试技术等，在现代机械工业中发挥着重要作用[1]。由于数控机床是一种复杂的机械结构，发生故障的可能性随着机床的复杂性而增加，降低数控机床的可靠性。因此在实际加工中，有些故障需要尽早避免，以确保数控机床的加工精度和稳定性。

传统的数控机床故障预测的实现都是基于丰富的实验数据，通常需要大量的故障信息才能准确预测，使得预测难度加大[2]。由于数控机床在全国应用范围较为广泛，收集故障信息数据需要大量的时间和财力，同时随着数控机床更新换代频率的增加，很难创建大数据库[3]。在数据匮乏的情况下，准确预测数控机床故障是目前需要研究的重点[4]。

目前，遗传算法优化长短期记忆神经网络广泛应用于各个领域，但将它应用于数控机床故障诊断还未做深度研究。本文作者采用遗传算法(Genetic Algorithm，GA)优化长短期记忆神经网络(Long Short Term Memory，LSTM)的超参数，并构建预测数控机床故障的网络模型预测机床故障，并获得最小预测误差。

1 数控机床故障分析

在研究数控机床的可靠性之前，有必要收集故障数据。获取数据的先决条件是：(1)真实性，即记录出现故障的时间和表现方式；(2)连续性，即故障数据记录必须持续，出现的任何故障都需要记录；(3)完整性，应清楚记录关于机床的使用状态、工作环境、维护时长和方法等基本信息。

在特定的条件和时间内，数控机床的某些性能指标无法保持在特定范围以及数控机床在特定条件下和特定时间对人、环境、能源、材料等的影响超过允许范围等[5]，都可视为出现故障，数控机床无法按时完成规定条件下的任务。根据数控机床故障的各种原因，可分为相关故障和非相关故障。由产品本身缺陷引起的相关故障，包括零件损坏和零件在生命周期内磨损引起的故障。非相关故障是指无特定条件或其他外在因素(如人为因素导致的操作错误或安装错误)而导致的故障[6]。

数控机床是一种复杂的机械结构，其故障受到许多因素的影响。根据触发因素的特点，故障类型可分为突然发生型和渐进发生型。突然发生型故障是由于机械变形、加工零件损坏或故障，加工设备失去某些功能等。这种类型的故障可能会导致机床停止，如主轴停止旋转、固定装置无法打开或关闭操作等[7]。这种情况往往规律性较差，故障预测无法解决。而渐进式故障是随着机床零件长时间工作、老化和逐渐磨损等导致的故障。由于机床运行时间和加工量的积累，数控机床的精度会降低。通常此类故障不会导致机床突然停止，但会影响加工零件的质量，导致加工精度不足、噪声振动增加或磨损严重等[8]。这种故障隐藏在实时加工状态中，也是文中研究的重点内容。

整理收集的10部数控机床一年内出现的故障数据，由于数据量大，先对它进行预处理。不讨论并删除因操作人员或维护人员操作不当和其他非相关问题而导致的人为因素。划分和整理相关故障数据共有100组。

数控机床的故障可根据子系统分为3种类型：数控系统的故障、电气系统的故障和机床机械部件故障[9]。数控和电气系统通常具有内部自我诊断功能，并通过成熟的报警代码进行维护，不需要考虑故障预测。文中重点研究机床机械部件故障。

为了更好地了解机床机械部件故障，根据出现故障的功能部件分布情况进行划分和分析。以现有开放式数控系统S-100M实验平台为例，首先，根据功能类型，除数控系统和电气系统外，数控车床按照主次又分为6个子系统：主轴系统、进给系统、刀架系统、液压系统、伺服装置、其他辅助系统[10]。为直观体现发生故障的部件，各子系统发生故障的概率如图1所示。

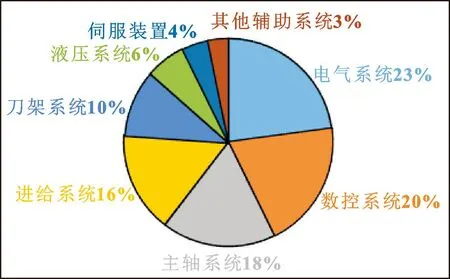
图1 系统故障统计Fig.1 System fault statistics

由图1可知：除数控系统和电气系统外，主轴系统、进给系统出现故障的次数较多，且这2个系统对加工误差影响也较多，也是文中实现预测的重要部分。

2 长短期记忆神经网络介绍

长短期记忆神经网络的特点在于以细胞状态为模型特征，可选择性地保留一些状态，遗忘一些状态，负责在任何时间段“保存”数据。由于存在细胞结构，无论分类或预测，LSTM都是一个非常适合处理时间序列数据的模型[11]。此外，与之前的模型相比，LSTM可以从信息中获取长距离数据，因此在长序列中表现更好。

LSTM内存单元中有输入门、遗忘门和输出门3个门。其中的任何一个都可以被视为传统的人工神经元，通过激活功能来计算总权重。当模型处理数据信息时，由输入门判断哪些数据需要存入存储单元；进入存储单元的数据由遗忘门选择满足需求的即为有用数据，其余数据删除；有用数据经过处理后将最终数据传递至输出门，得到最终输出值[12]。LSTM的内部结构如图2所示。

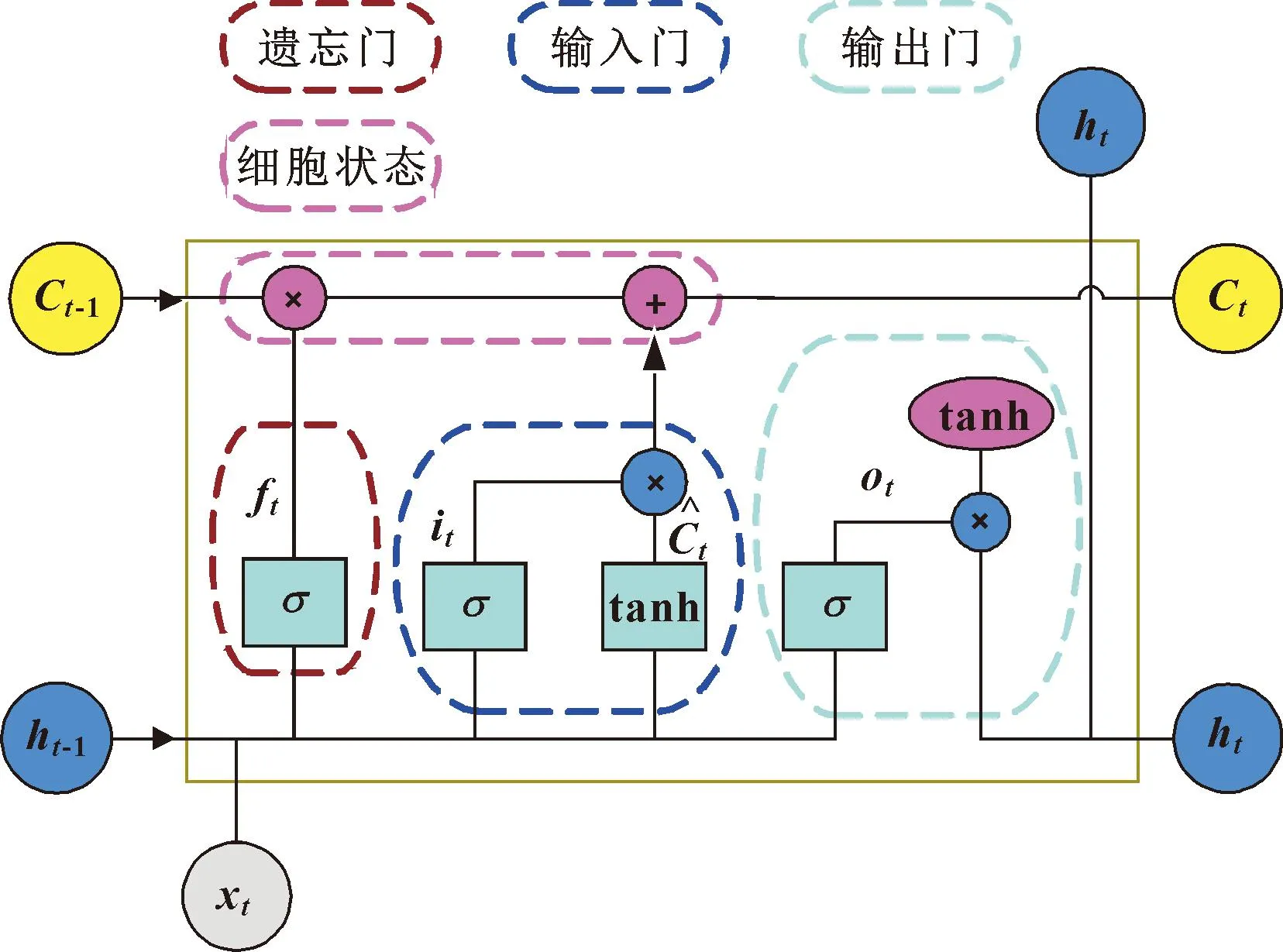
图2 LSTM的内部结构Fig.2 Internal structure of LSTM

输入门的功能是有选择地在细胞状态中记录和识别新信息，并存储在细胞状态中。输入门以σ层和tanh层的形式存在。σ层决定更新值，tanh层生成新的内存，并添加有关删除属性等其他信息。公式如下：

it=σ(Wi×[xt，ht-1]+bi)

(1)

(2)

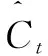
ot=σ(Wo×[xt,ht-1]+bo)

(3)

ht=ot×tanh(Ct)

(4)

式中：Wo代表权重；bo代表偏置；ht为隐藏层最终输出。

遗忘门的任务是有选择地过滤细胞状态的信息，并选择性地遗忘[13]。通过接收前一单元的输出Ct-1并选择保留或遗忘Ct-1的部分，公式如下：

ft=σ(Wf×[xt，ht-1]+bf)

(5)

(6)

式中：xt是t时刻神经元的输入；ht是神经元的输出；Wf代表权重；bf代表偏置；σ是神经元sigmoid激活函数；ft是遗忘门的结果。

LSTM的一大优势在于考虑了对时间特征连续事件的依赖性。LSTM使用专用的单元取代传统的神经元[14]。在LSTM中，内存块包含输入和输出等特定元素，允许LSTM更新和监视每块中的信息流。使用输入、输出和遗忘门不断更新预测，这种能力使得LSTM在短期内对机床故障预测相对有用。

3 GA-LSTM预测模型

3.1 模型构建

由于LSTM模型中有许多超参数需要手动调整，例如隐藏层中的神经元数量、初始学习率、最大迭代次数、最小处理量和时间步长等，这些超参数对预测结果有一定影响[15]。找到最佳超参数是文中需要解决的问题。遗传算法是一种仿生优化算法，能够模拟生物体的进化。它用于改善超参数，并使用从种群持续遗传进化过程中发展的一组具有最佳能力的参数模型，在此组参数框架内获得模型的最优结果。因此，遗传算法被添加到优化LSTM模型标准中，以创建GA-LSTM预测模型。文中提出的GA-LSTM模型(见图3)由以下四部分组成：

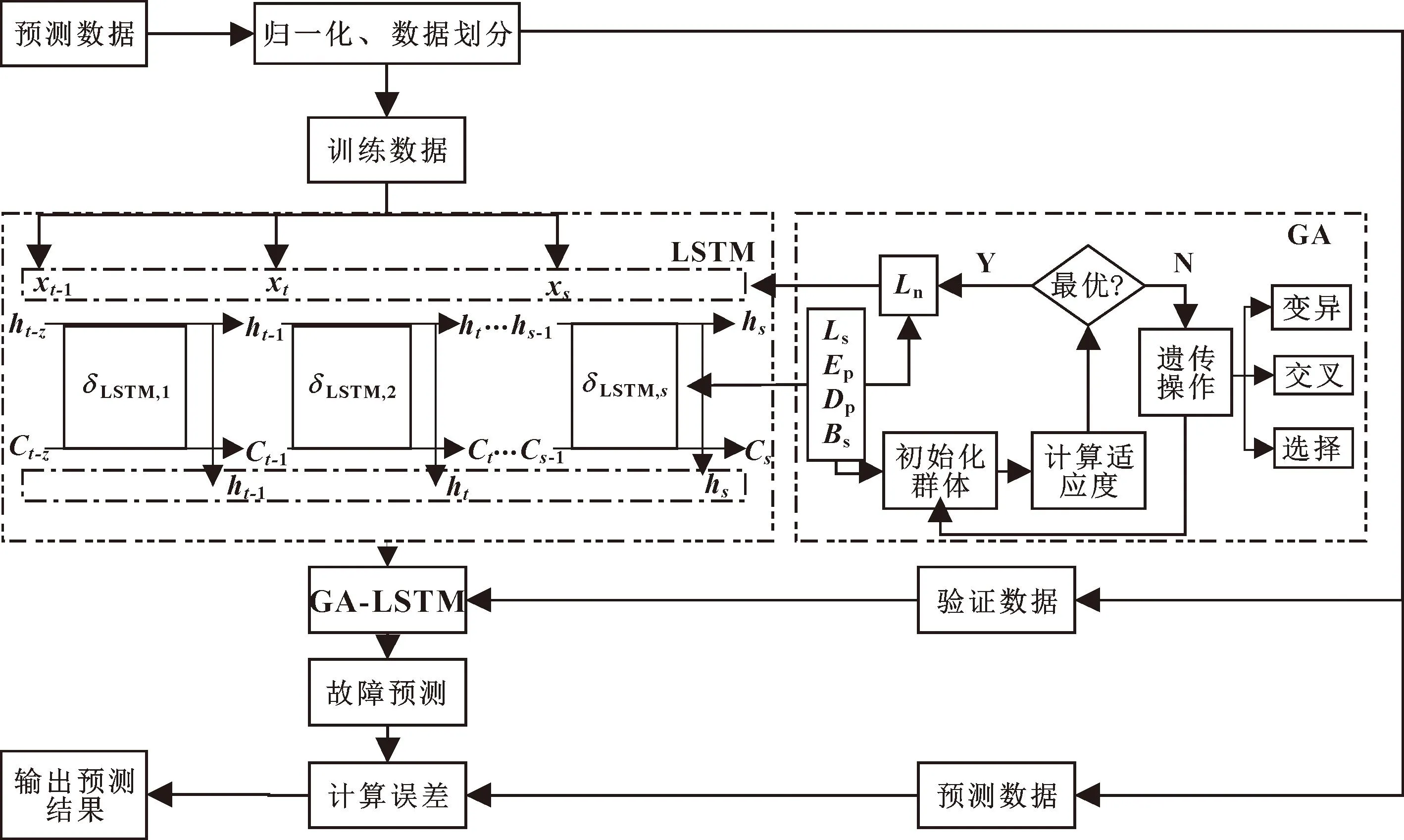
图3 GA-LSTM预测模型流程Fig.3 Flow of GA-LSTM prediction model

(1)输入层。将划分后不同时刻的传感器数据xt传入到LSTM网络中，以获得预处理后的传感器数据集。例如经过清理、标准化等操作，消除数据之间的关系，降低复杂性与机床故障关联最小的数据计算。

(2)LSTM层。进入输入层的数据输入到LSTM网络中进行权重W和偏置b处理，以提取数据时间属性。将xt-1输出层数据传递到当前xt层作为输入，得出ht，然后再将输出数据作为xt+1层输入，此时xt+1层即为第二个LSTM层的输入。xt-1接收到数据以获得隐藏的ht输出层进入下一步长；为了确定输入和输出之间的逻辑关系，采用多层LSTM层提取隐藏在时间数据中的时间特征[16]。最后，LSTM网络层的输出值即可通过多层处理获得。

(3)GA层。为了实现优化，提高预测准确性，利用GA遗传算法的特性，最终确定LSTM模型各层实际参数。

(4)输出层。输入数据与数控机床故障之间的关系是LSTM网络的主要关联。从LSTM层获得结果传递到全连接层，并根据加权求和转换为输出层进行判断，获得机床输出状态。

3.2 预测思路

文中提出的GA-LSTM模型中，为了及时提取隐藏信息，应考虑增加LSTM层的深度。一方面，可以通过深化LSTM层来识别复杂环境中的故障样本，从而创建堆叠LSTM网络[17]。另一方面，为了提高可预测性，可以增加总联接层的层数并调整神经元的数量。

通过修改和设计结合遗传算法的LSTM神经网络，其模型的超参数可实现优化。该模型用于训练和预测数据，最终获得数控机床故障的预测值。具体模型和预测思路如下：

(1)拆分和处理数据集。文中选择数控机床中常见故障的数据进行训练，使用常见故障中较容易出现的故障数据进行验证，测试大概率出现的故障数据。同时，数据集已标准化。

(2)设计LSTM结构模型。文中设计的LSTM模型的网络结构包括隐藏层数量、学习速度和迭代次数等，以构建多变量、多维单步LSTM神经网络模型。

(3)遗传算法改善模型参数。针对LSTM模型超参数例如隐藏层中的神经元数量、初始学习速度、最大迭代次数、最小批处理量、时间等参数进行调节，获得最佳的超参数组。

(4)使用最佳GA-LSTM模型对训练集进行训练以获得最终模型。

(5)使用最终模型进行预测测试，获得数控机床故障的较高准确性预测。

4 实验测试过程与结果讨论

基于上述GA-LSTM模型的预测步骤，分析已有的开放式数控系统S-100M实验平台在2017-2022年选取的故障数据，整理出150组样本数据，选取其中70%的数据作为训练集、30%的数据作为测试集。 由于直线插补是数控加工中最基础的运行过程，且刀具切削运行较为稳定。因此，文中仅预测数控系统加工直线插补运行过程中出现误差的可能，运行过程如图4所示。若选定其他工况(如圆弧插补等)，还需考虑实行曲线轨迹走刀时，切削加速度波动、曲率半径大小、走刀状态是否稳定等因素对模型的预测结果的影响，在后续实验中进一步研究。

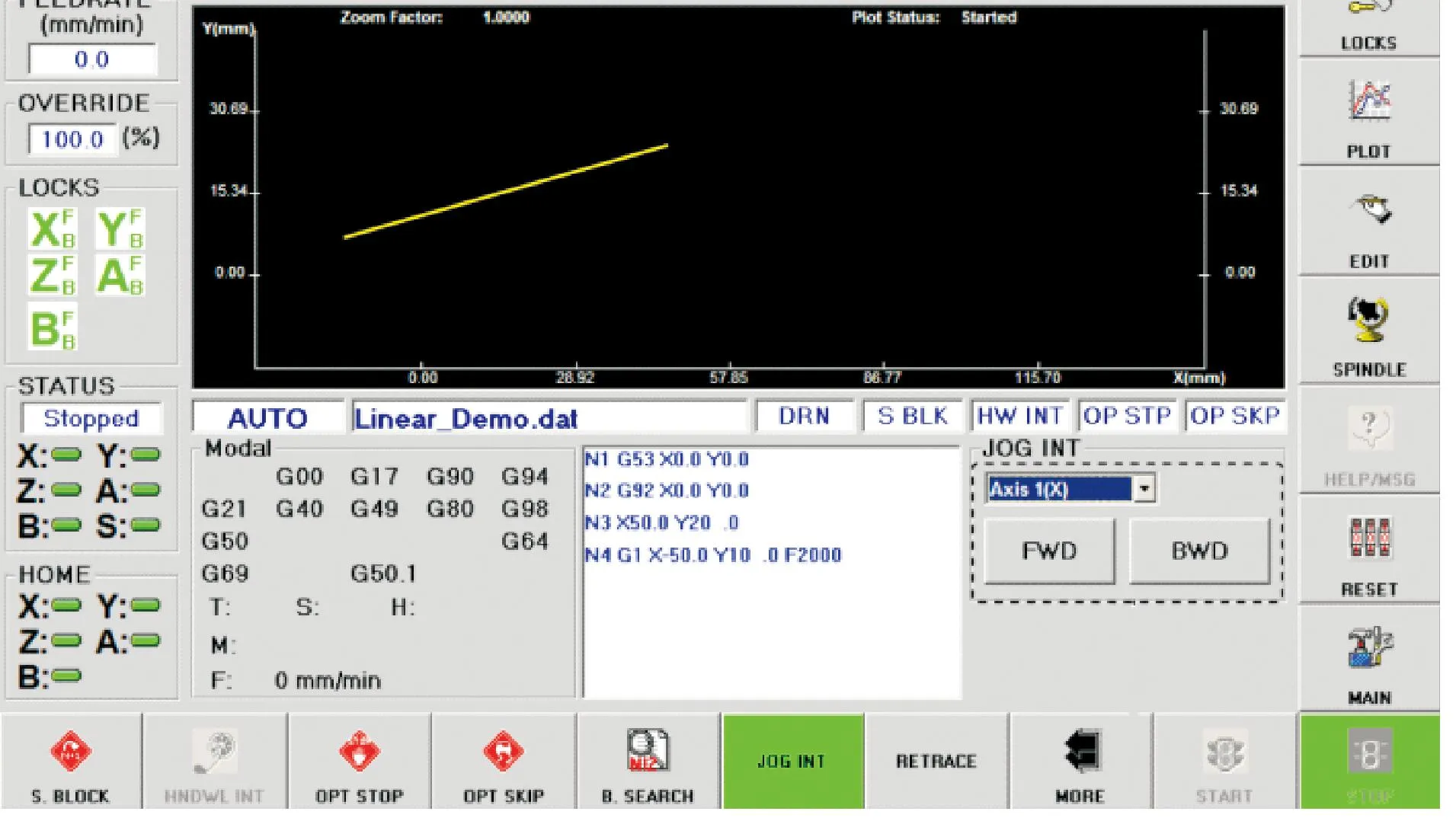
图4 加工路径Fig.4 Processing path

在MATLAB软件中设置相应程序代码，设置时间步长为1，隐藏层节点为200，输出层神经元个数定为1，求解器设置为′adam′并进行50轮训练。学习率为0.01。图5分别显示BP、LSTM、GA-LSTM 3种模型的预测状态对比。

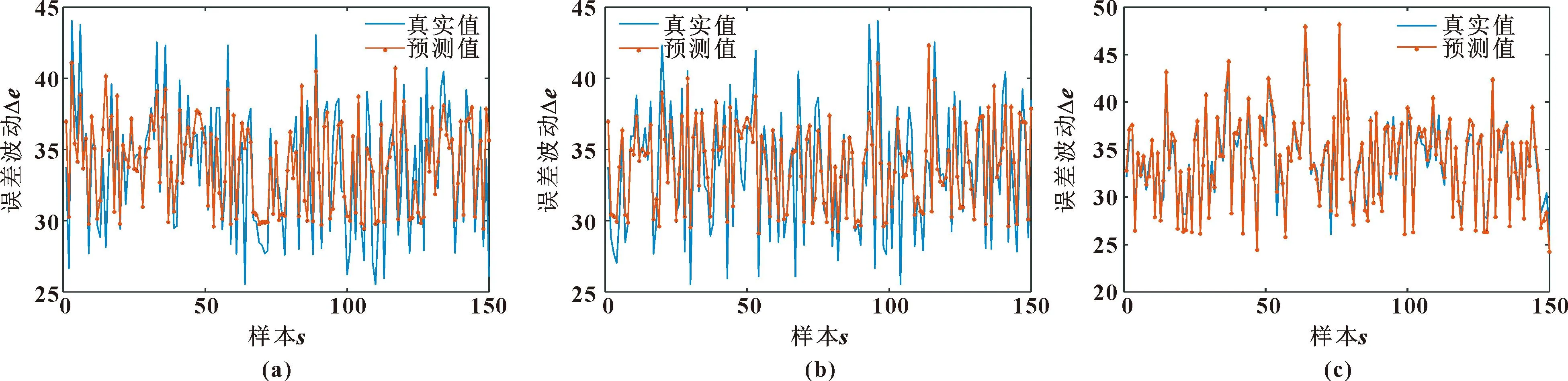
图5 BP(a)、LSTM(b)、GA-LSTM(c)预测状态对比Fig.5 Comparison of BP(a)，LSTM(b)and GA-LSTM(c)prediction states

将BP、LSTM、GA-LSTM 3种模型的预测状态相关数据进行对比，如表1所示。GA-LSTM预测模型相比其余常规预测方法的运行时间有所减少，相对误差明显减小，预测误差状态更趋于真实值。

表1 3种模型均方误差与预测误差对比Tab.1 Comparison of mean squared error and prediction error of the three models

5 结论

综上所述，数控机床故障预测是提高数控加工误差精度的基础。通过实验测试结果得出以下结论：

(1)通过分析数控机床常见故障类型，对常见加工路径过程进行分析，建立了基于GA-LSTM的机床故障网络预测模型，通过优化隐藏层节点、训练次数等超参数，实现了对数控机床故障的准确预测。

(2)相比其余常规预测方法，GA-LSTM预测模型运行时间有所减少，预测误差状态更趋于真实值。

(3)文中所提出的GA-LSTM模型用于预测数控机床故障时具有一定可行性。