基于FTA优化CPSO算法的锻压机典型故障诊断研究
2024-01-16赵燕燕汤瑞习岗俞生伟
赵燕燕,汤瑞,习岗,俞生伟
(1.郑州西亚斯学院电信与智能制造学院,河南郑州 451100;2.开封技师学院汽车工程系,河南开封 475000;3.西安理工大学理学院,陕西西安 710048;4.杭州大华仪器制造有限公司,浙江杭州 311400)
0 前言
金属锻压已经成为现阶段部件成型加工的一种重要技术,而锻压机则是其加工过程所需的一种关键成型设备[1]。为适应多种类型的产品加工需求,要求锻压机具备良好的通用性并可以实现高度自动化控制的功能,同时满足锻压、冲压等各类产线的加工过程[2-3]。采用智能诊断方法可以实现故障大规模诊断的功能,同时达到智能调控的效果。根据现有报道可知,已有多种智能诊断方法实现了诊断设备运行故障的功能[4]。当系统较复杂时,则难以建立准确的故障树模型,通常采用遗传算法实现运行设备的故障诊断,获得良好的诊断性能[5-6]。虽然利用遗传算法有助于刀具达到更高故障诊断准确率,但较易造成局部最优,而且采用这一算法需要编制复杂的程序,极大提高了整体处理过程的难度[7]。董伟航等[8]利用人工神经网络方法对机床伺服控制系统运行故障进行了诊断测试,实现了故障诊断精度的大幅提升,并且缩短了诊断过程的处理时间。考虑到人工神经网络方法只能存储很少的故障数据,因此利用模糊理论实现机床刀架故障诊断。由于模糊理论分析方法缺乏良好的学习性能,较易出现错误的判断结果[9]。杜柳青、李仁杰[10]采用粒子群算法对模拟电路的故障进行诊断分析,此算法具备快速收敛以及易于建模的优势,相对其他算法可利用参数调整的方式实现局部寻优,同时实现故障信息的全局搜索功能,不需要复杂的操作过程。而在最初搜索的过程中会发生快速收敛,从而造成早熟以及需要进行大量计算的缺陷。张开哲等[11]针对锻压机转台轴承摩擦力矩精确度不足的问题,基于BP神经网络与二阶响应曲面法,提出了基于BP神经网络与二阶响应曲面法的预测方法。
采用单一故障诊断算法也会造成较多的问题,包括无法获得高的故障诊断率以及需要设置复杂的诊断措施等[12]。为获得更优的诊断效果,本文作者运用故障树分析与混沌粒子群相结合的方式实现故障诊断。
1 FTA优化CPSO故障诊断方法
从锻压机故障产生的部位可知,它包含主控结构、主轴结构、伺服结构、液压结构、润滑结构等,文中重点研究了锻压机伺服结构运行过程中的故障诊断。为了对伺服结构故障进行准确、高效的诊断,综合运用FTA与CPSO的优势进行了优化计算,由此完成伺服故障树测试。
1.1 伺服系统故障树分析
锻压机伺服结构是在外部指令的作用下达到运动控制的过程,可以通过小功率指令对高功率负载进行控制,确保机械动作与电信号之间保持高精度匹配状态,从而在不设置机械连接的条件下,达到远距离的传动控制效果。伺服系统在运行阶段容易发生故障问题[13],结合前期研究结果[14],可以将锻压机伺服系统的故障分为继电器有误、机床达到极限、电流负载过大、开关失灵、电机永久磁体去磁、绕组内部短路等形式,得到图1所示的故障树。

图1 锻压机伺服系统故障树Fig.1 Fault tree of forging press servo system
1.2 伺服系统故障的CPSO分析
文中首先计算系统运行时FTA故障发生的概率,由此构建FTA-CPSO锻压机故障诊断法,之后利用CPSO实现精确的故障诊断。根据以上分析确定系统故障特征与概率。下面通过CPSO分析了锻压机伺服系统的故障[15]。
总共设置5个传感器作为伺服系统欠压报警故障的采集部件,各组数据分别为一个粒子,所有粒子组成故障种群,再将它置于D维搜索空间内,构建的D维向量Xj代表第j个粒子位置对应的变化率,CPSO粒子可以记录搜索阶段的最佳位置Xp,后续迭代时继续更新粒子速度与位置以获得合适的搜索路径。
式中:W表示惯性权重,该参数是粒子保持原有运动状态的能力,随着惯性权重的增大,收敛速率也更快,处于较小惯性权重下时,则可以有效消除局部极值的问题;c1与c2为学习因子,有利于粒子运动到最佳位置;r1、r2都是取值介于[0,1]之间的随机数。进行最优粒子搜索时,容易产生局部最优的结果,此时可以通过混沌扰动的方式克服。
以下为混沌扰动的具体处理过程。先对最佳粒子位置进行映射计算,使它转化为定义域[0,1]内的值,具体计算过程为
按照以下公式获得混沌变量可行解适应参数:
当迭代至最大次数时,搜索范围大幅缩小,同时对较差粒子起到替换的作用。
采用FTA-CPSO算法诊断锻压机运行故障的步骤如下:
(1)首先构建锻压机的故障树,确定系统最小割集并计算故障概率,按照从大往小的顺序对故障概率进行排序;
(2)选择最大故障概率为目标粒子,通过CPSO算法获得最优搜索,并确定最佳粒子;
(3)比较搜索粒子和目标粒子,判断是否完成全局搜索条件;
(4)通过CPSO算法继续搜索最优粒子,并跟目标粒子进行对比分析;
(5)当条件符合时,搜索过程结束;当条件不符合时,重复执行步骤(2)(3)(4),直至各类故障模式都完成搜索过程。
图2所示为故障诊断的具体流程。
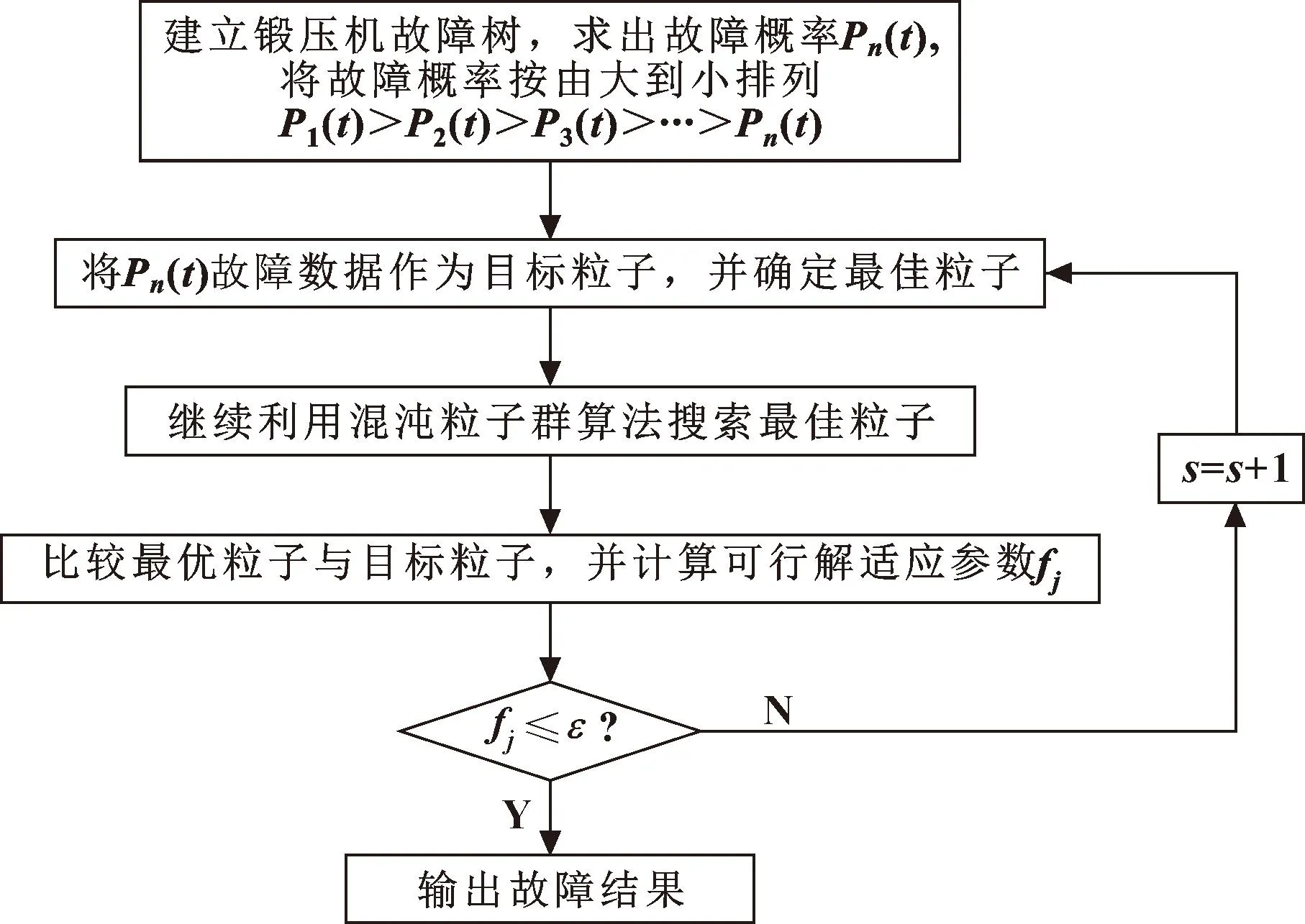
图2 故障诊断流程Fig.2 Fault diagnosis flow
2 实验结果分析
文中对BXS-300T型锻压机开展了研究,测试现场如图3所示,以DPS系统完成锻压机各项运行参数以及故障信号的采集。持续测试7 d,再分析伺服系统的故障。

图3 测试现场照片Fig.3 Test site photos
为测试FTA-CPSO算法诊断锻压机故障的可靠性,将该算法和遗传算法(GA)以及PSO算法进行了伺服系统故障诊断的性能测试对比。此次测试总共采集得到6种欠压报警故障测试参数。经过初期预处理后获得包含1 000组样本的测试集,该数据集内同时存在正常与故障数据。之后再从现有故障库内筛选500组故障数据进行训练。从表1中可以看到:样本数据包含了训练与测试样本2种类型。
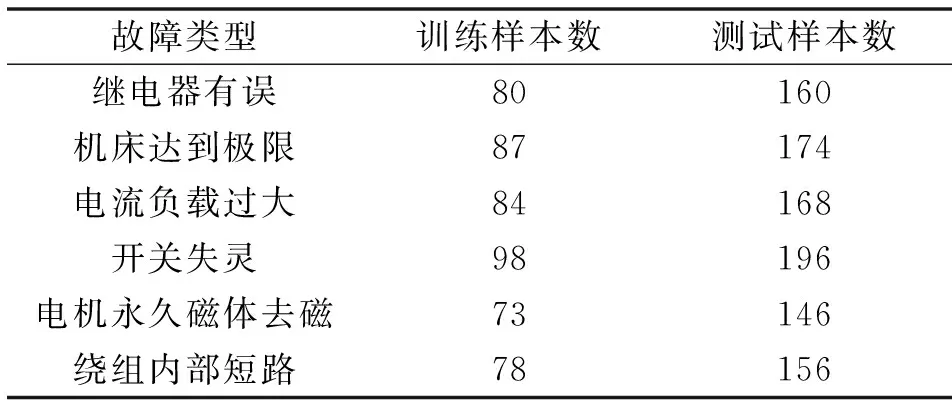
表1 样本数据的组成Tab.1 Composition of sample data
此实验选择MATLAB软件程序,总共设置了500组训练样本,依次对GA、PSO与FTA-CPSO实施训练。按照实际测试结果确定各项参数:将各算法种群大小设定在1 000,共迭代500次,对于PSO与FTA-CPSO 2种算法,同时将惯性权重设定为W=0.7,最大搜索步长为8,g为0.09,根据文献[7]设置其他参数。算法训练结果见表2所示。

表2 算法训练结果Tab.2 Algorithm training results
对以上训练情况进行分析,在训练后算法内输入1 000组样本数据进行测试,分别以3种算法诊断欠压报警故障获得表3所示各项参数。分析表3可以得到:GA、PSO与FTA-CPSO依次达到了92.01%、94.06%与98.26%的准确率,其中,FTA-CPSO算法的故障诊断准确率比GA高6.25%,比PSO高4.20%。由此可以判断,FTA-CPSO相对GA与PSO实现了准确率的显著提升。从表3中可以看到:分别以3种算法进行故障诊断时的均方差依次为0.19、0.12与0.04,其中,GA相对FTA-CPSO具有了4倍以上的诊断率均方差,PSO相对FTA-CPSO具有了3倍的诊断率均方差。对各算法进行寻优测试发现,GA与PSO的寻优误差较大,以FTA-CPSO算法进行处理可以获得较小的误差,相对GA与PSO达到了更优诊断性能。

表3 诊断结果Tab.3 Diagnosis results
之后采用文中设计的FTA-CPSO算法测试了锻压机故障诊断的收敛性能。分别对各算法的适应值在不同迭代次数下达到的收敛状态进行测试,结果见图4。可以发现:经过多次迭代后,此实验所有算法的适应值都有减小的趋势。GA诊断样本故障的过程中迭代约260次,达到了0.089的适应值。对样本进行PSO故障诊断时,迭代约250次后适应值趋于稳定,其值为0.086。FTA-CPSO算法进行200次迭代运算后其适应值也趋于稳定,值为0.080。根据图4可以发现,FTA-CPSO可以在最短时间内完成迭代计算。
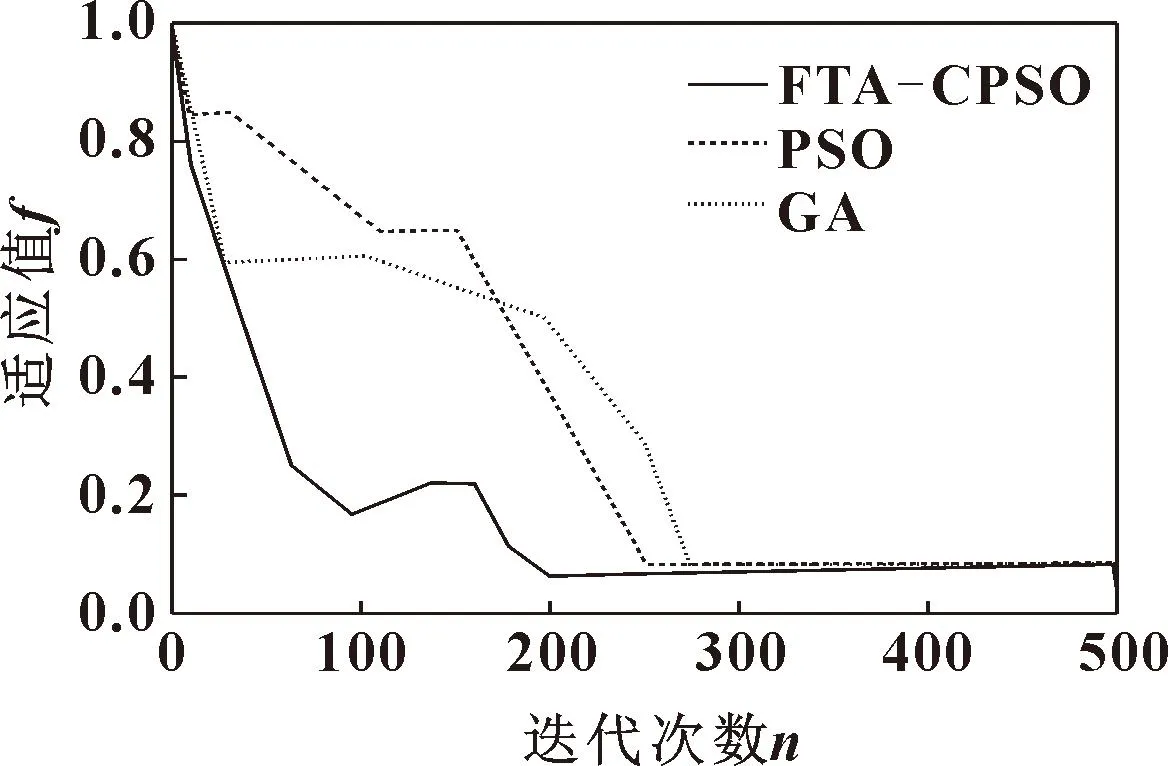
图4 适应值随迭代次数变化Fig.4 Adaptation value changes with the number of iterations
FTA-CPSO算法通过故障树分析的过程计算出故障模式概率,再根据CPSO算法搜索获得较大概率的故障。可以有效降低迭代次数,同时搜索时间也明显缩短,还可以有效避免产生局部极值的问题,大幅提升了诊断精度。
3 结论
文中开展基于FTA优化CPSO算法的锻压机典型故障诊断研究,取得如下有益结果:
(1)FTA-CPSO算法的故障诊断准确率比GA高6.25%,同时比PSO高4.20%。FTA-CPSO算法可以获得较小的误差,相对GA与PSO达到了更优的诊断性能。
(2)经过多次迭代后,此实验所有算法的适应值都减小。FTA-CPSO可以在最短时间内完成迭代计算,可以有效降低迭代次数,同时搜索时间也明显缩短。
