基于Sobel算子的池化算法设计
2023-03-15冯松松王斌君
冯松松,王斌君
(中国人民公安大学信息网络安全学院,北京 100038)
卷积神经网络(convolutional neural networks,CNN)是根据生物视知觉原理构建的前馈神经网络,可对输入信息按设计的阶层进行平移不变分类,适用于有监督学习和无监督学习任务。卷积神经网络最早可追溯到1979—1980年福岛邦彦模拟生物视觉皮层机制提出的“neocognitron”深度神经网络[1],初步实现卷积层和池化层功能,可对特征进行提取、筛选,对后续卷积神经网络的发展具有启发性意义。
Waibel等[2]首次将卷积神经网络用于语音识别,设计出了时延卷积神经网络(time delay neural network,TDNN)算法,并采用反向传播机制进行训练,获得了圆满的效果,优于同时期的主流语音识别算法隐马尔可夫模型(hidden Markov model,HMM)等。
LeCun等[3]提出适用于计算机视觉问题的LeNet,它包含卷积层、全连接层,并用随机梯度下降(stochastic gradient descent,SGD)进行学习,结构上已接近现代卷积神经网络。同时期,随着支持向量机(support vector machine,SVM)等核学习方法的流行,对卷积神经网络的研究热度逐渐降低。Hinton等[4]正式提出深度学习(deep learning)概念,开启了现代深度学习研究新纪元。深度学习源于人工神经网络的研究,是机器学习的一种,目前,卷积神经网络、深度神经网络、深度信念网络等深度学习模型已成功应用于计算机视觉、自然语言处理、语音识别等众多领域,硕果显著。
此后,得益于硬件设备计算能力的提升,以及大数据时代的到来,AlexNet[5]、ZFNet[6]、VGG[7]、GoogLeNet[8]、ResNet[9]、DenseNet[10]和UNet[11]等一系列深度卷积神经网络被提出,广泛应用于不同计算机视觉任务中;此外TextCNN[12]、DPCNN[13]、TextRCNN[14]等卷积神经网络在文本分类等自然语言处理任务中也取得显著成果,这些成就和实质性的进展,极大地推动了卷积神经网络的深入研究和蓬勃发展。
现代卷积神经网络由输入层、多个隐藏层、输出层3个主要模块组成,其中,每个隐藏层通常还可包含卷积层、池化层等。不同的网络结构设计,实现的效果也有较大差别。通常池化层可实现特征选择、缩小参数矩阵、降低特征维度的功能。此外,池化操作还具有扩大感受野等作用。
在实际使用中,为更好地保留内容和风格特征,减少特征信息损失,研究人员根据整体模型架构提出了不同的池化方法。本文按池化结果与池化窗口内单个点的值或多个点的值有关,将现有的池化方法分为单值策略和多值策略。下面分别进行阐述。
(1)单值策略。这类池化算法中最具代表性的是最大池化。最大池化是取每个池化窗口内的最大值,能很好地保留最强的纹理、轮廓等特征,但会淡化其它纹理特征以及整体背景风格等信息。
He等[15]提出空间金字塔池化(spatial pyramid pooling)方案,在该池化算法中,作者使用不同尺寸的最大池化核对特征图进行池化,对得到的池化结果进行拼接,获得了多个尺度上的特征,丰富了感受野。
Wu等[16]提出最大池化失活(max pooling dropout)方案,作者指出在训练时使用最大池丢失等价于具有可调参数的多项分布抽样激活,本质是对池化窗口内部分元素进行随机失活,再取余下元素的最大值。此外,Zhai等[17]还提出随机采样池化等。
(2)多值策略。平均池化是多值策略的代表,平均池化是对池化窗口内的所有元素求均值,降低了估计值方差,能很好地保留整体风格特征,但会弱化纹理、轮廓等信息。
Deliège等[18]提出顺序池化(ordinal pooling)方案,将每个池化窗口内的元素按顺序排列,并根据对应位置的权重计算求值,其中权重是在训练中学习得到的。顺序池化考虑到了池化核内的每个元素,减少了特征信息的丢失,但计算复杂度较大。
Rippel等[19]提出谱池化(spectral pooling)方案,基于快速傅里叶变换,对特征图进行离散傅里叶变换,通过截断频域实现特征降维,再经过傅里叶逆变换得到池化结果。谱池化具有滤波功能,在保存低频变化特征的同时可灵活调整输出维度。整体保存了更多特征信息。但是,计算量大,训练时间长。
刘砚萍等[20]提出引入少量可学习参数的自学习池化算法,对不同特征通道进行独立池化,并给池化层可学习权重添加正则约束项,增加算法的鲁棒性。
此外Stergiou等[21]提出基于Softmax加权的池化方案,Gong等[22]提出多尺度无序池化(multi-scale orderless pooling),Gao等[23]提出基于局部重要性的池化,Sharma等[24]提出引入模糊逻辑的模糊池化,Wan等[25]提出基于信息熵的特征加权池化,Lin等[26]提出用于特征融合的双线性池化,Arandjelovic等[27]提出局部特征聚合的NetVlad池化,王宇航等[28]提出基于高斯函数的加权平均池化等均属于多值池化方案。
除上述两种基本的池化方法外,Yu等[29]提出混合池化(mixed pooling)方案,在最大池化和平均池化中随机选择,结合了两种经典池化方案的优点,丰富了特征层,一定程度上解决了过拟合问题,但普适性较差。
针对上述各池化算法存在的问题,在设计全新的池化算法时,将考虑特征图整体的内容及风格特征分布,有选择性的进行池化,在保持池化前后特征图的内容、风格特征分布一致的情况下,稳定提高模型准确率,并且可用来替代常用的最大池化、平均池化,成为一种通用的池化算法。
1 池化算法设计
池化的最终目的是对特征图进行降采样,在降低模型参数量的同时,尽量减少特征信息的损失,保持池化前后特征图的不变性。当前,常用的池化方法是在池化窗口内取某个代表值(如最大池化)或多个值的加权(如平均池化),同一池化层采用相同的策略。一般来说,单值策略能更好的保持特征图的某些内容特征,而多值策略则能更好的保持图像的整体风格特征。因此,现有的池化方法要么导致池化前后特征图的均值保持接近,要么导致池化前后特征图的标准差保持接近,二者难以兼顾。
受人眼视觉系统更关注图像中的边缘区域以及视觉皮层分级处理视觉信号的启发,在对卷积后的特征图进行池化时,不仅要保留池化域中的最大值、平均值,还需保留一部分最小值。保留部分最小值有两个好处,一是使池化前后特征图的均值、标准差分布保持一致,特别是能减少整体特征的损失;二是使池化后的特征图有明显的对比,边缘清晰,便于后续进一步识别。为此设计全新的池化算法,根据特征图中风格特征、内容特征的分布,合理地选择池化窗口内的最大值、平均值或最小值作为池化结果。
1.1 Mam池化算法
为保持池化前后特征图中的风格特征、内容特征不变,在对同一卷积后的特征图池化时,不仅要选择池化窗口内的最大值、平均值作为池化结果,还要有一部分池化窗口选择最小值,保持池化前后特征图的均值、标准差分布一致。
Mam(maximum-average-minimum)池化算法的设计思路是对池化窗口进行划分,即一部分池化窗口取最大值;一部分池化窗口取均值,还有一部分池化窗口取最小值。划分的依据为每个池化窗口的均值Avg(aij)与整个池化域的均值mA和标准差sA的加权做比较。以非重叠池化为例,池化核大小、步长均为k,aij=A[k*i:k*i+k,k*j:k*j+k]表示池化域中的每一个池化窗口。其中,i,j表示池化后特征图的第i行、第j列,*表示卷积操作。具体池化过程表达式为
(1)
式(1)中:A表示池化前特征图;B表示池化后特征图;α、β为可调节参数。
Mam池化算法的优点是实现简单,便于理解,引入的额外计算量小。缺点也很明显,并没有考虑每个池化窗口内的特征分布与整个池化域的内容特征、风格特征分布之间的内在关联,而是简单根据整个池化域的均值、标准差对不同池化窗口进行划分,在实际使用中表现不佳。
1.2 Sobel池化算法
理论上讲,Mam池化算法能保持池化前后特征图的整体内容和风格特征分布一致。为使池化更能充分体现整体风格、主要内容等特征的分布,本文使用了Sobel算子对卷积后的特征图进行处理,得到每个像素点的梯度值,并根据梯度值大小分布选择池化窗口内的最大值、均值或最小值做为池化结果。
1.2.1 Sobel算子
Sobel算子是基于一阶导数的离散性差分算子,对像素值变化更为敏感,常用作对数字图像进行边缘检测。在进行边缘检测时,Sobel算子对周围像素的重要性根据位置进行加权求值,边缘检测效果较好。
Sobel算子包括检测水平边缘的gx算子[图1(a)]和检测竖直边缘的gy算子[图1(b)],本文中在使用Sobel算子进行边缘检测时,只保留梯度值,不考虑梯度方向。
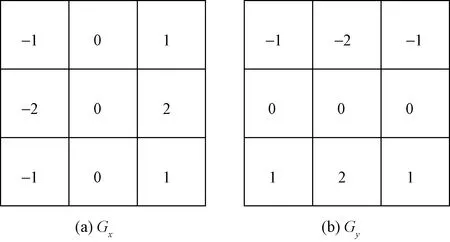
图1 Sobel算子Fig.1 Sobel operator
计算每个像素点梯度值的流程如下:
(1)用gx算子在图像A上做卷积(*)操作检测水平边缘,即
Gx=A*gx
(2)
(2)用gy算子在图像A上做卷积操作检测垂直边缘,即
Gy=A*gy
(3)
(3)结合水平方向和垂直方向计算图像A中每一个像素点的梯度值,即
G=|Gx|+|Gy|
(4)
1.2.2 Sobel池化算法
池化也称降采样,旨在对输入的特征图进行压缩,减少冗余信息,合理的池化算法能在减小模型参数量的同时,最大程度保留关键特征。为使池化前后特征图中内容特征、风格特征分布保持一致,将特征损失降至最小,先用Sobel算子对特征图进行边缘检测得到每个像素点的梯度值,对特征图进行池化时,考虑到池化窗口的梯度均值与整个特征图的梯度均值和梯度标准差之间的关系,确定取该池化窗口内的最大值、均值或最小值作为池化结果[式(5)],使每个池化窗口的取值更合理。
具体实现过程如图2所示(以单个特征图池化为例),算法如下。
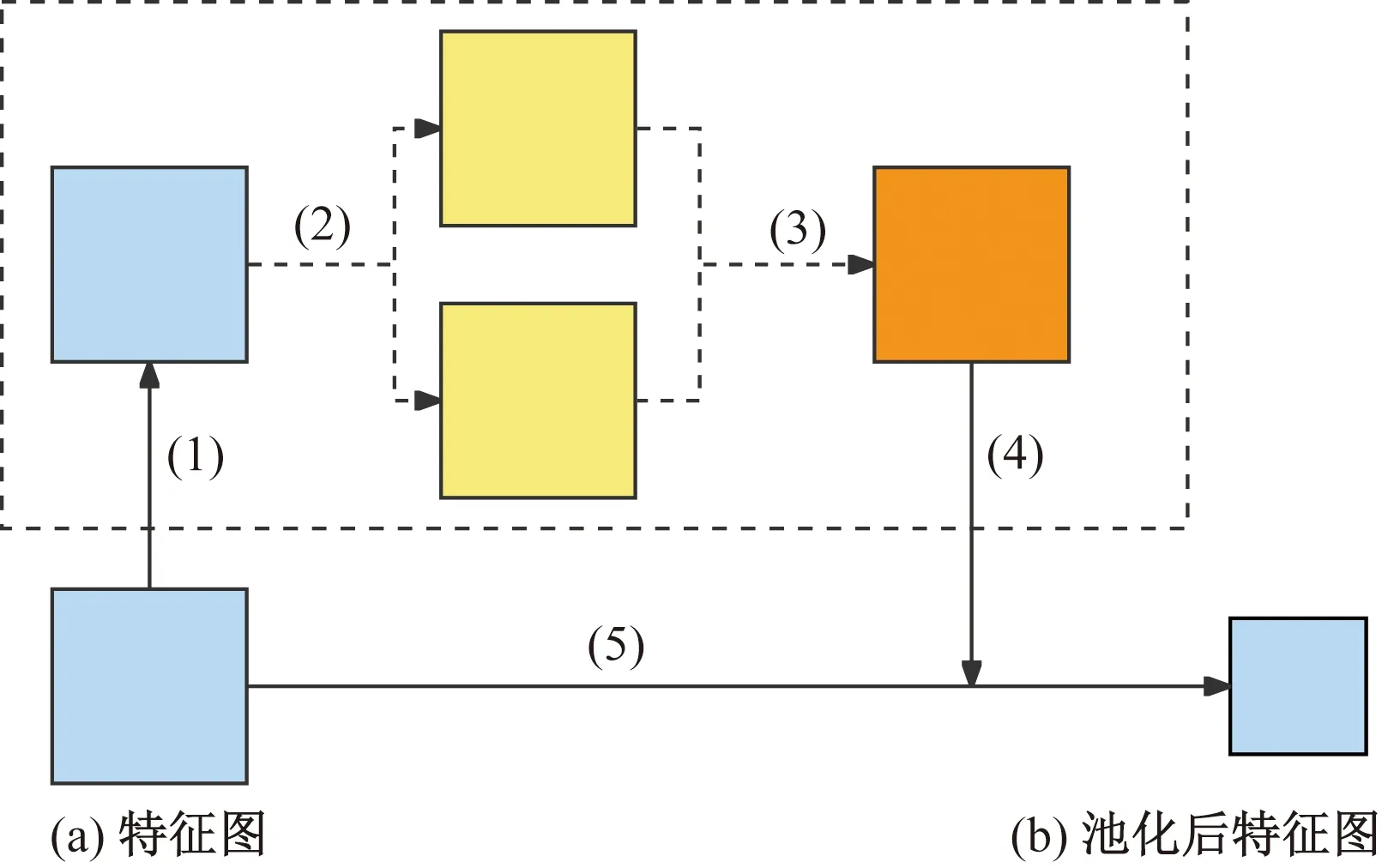
图2 Sobel池化流程图Fig.2 Sobel pooling flow chart
(1)对特征图A进行上、下、左、右为1的边缘复制填充,使采用Sobel算子计算得到的梯度图G保持尺度大小不变。
(2)对填充后的特征图进行水平[式(2)]、垂直[式(3)]两个方向的边缘检测求得Gx、Gy。
(3)采用式(4)合并Gx、Gy得到特征图中每一个点的梯度,求得梯度图G,不考虑梯度方向,只保留数值。
(4)对梯度图G求均值mG,标准差sG。以非重叠池化为例,按照池化核大小、步长k将梯度图G划分成多个k×k大小的池化窗口,对每个池化窗口分别求均值Avg(gij),其gij=G[k*i:k*i+k,k*j:k*j+k]。
(5)以非重叠池化为例,按照池化核大小、步长k将特征图A划分成多个k×k大小的池化窗口aij,其中aij=A[k*i:k*i+k,k*j:k*j+k]。对特征图进行池化,Avg(gij)大于mG+αsG的取特征图A中对应池化窗口内最大值作为池化结果,Avg(gij)小于mG-βsG的取特征图A中对应池化窗口内最小值作为池化结果,Avg(gij)介于mG-βsG到mG+αsG之间的取特征图A中对应池化窗口内均值作为池化结果,计算过程为
(5)
2 实验设计及结果分析
本节实验选择计算机视觉领域经典的分类任务来验证设计的池化方法能在不同图像分类模型、不同图像数据集上起到较好的分类效果。
进行实验的环境为一台4核心、16 G内存的服务器,操作系统为Windows10,并配有一张32 G显存的NVIDIA Tesla V100显卡,使用Python 3.7.13、Pytorch 1.11.0+cu113框架。
2.1 不同池化方法效果对比
为验证设计的Sobel池化算法对图像池化后,得到的图像层次更加分明、易于判别,选择了最大池化、平均池化、Mam池化做对比,直接对颜色、细节、纹理、对比度等各不相同的2 048×2 048像素高清图像连续进行4次2×2非重叠池化,采用各池化算法池化后的图像如图3所示。

图3 不同池化方法池化效果Fig.3 Pooling results of different pooling methods
从图3中可以看出:采用最大池化得到的图像只保留了每个池化窗口内的最大值,导致池化后图像像素均值高于原图,使图像整体偏亮,明、暗区域层次不明显;采用平均池化得到的图像保持了池化前后图像像素均值不变,但池化后图像像素的标准差小于原图,导致池化后图像边缘轮廓模糊,辨别度低;采用Mam池化、Sobel池化得到的图像,既保留了原图中的部分最大值,也保留了部分最小值,使得池化前后图像的均值、标准差变化较小,得到的池化图像轮廓清晰,明、暗区域层次分明,易于识别,但采用Mam池化算法得到的的图像存在亮的区域更亮、暗的区域更暗,而且边缘位置会向亮的区域偏移,出现失真,而本文中采用的Sobel池化算法能很好地均衡图像的明、暗区域分布,使得图像边缘轮廓更为清晰真实,易于识别。
2.2 不同经典模型在同一数据集上的表现
为验证设计的Sobel池化算法具有普适性,能够取代最大池化、平均池化,在VGG、ResNet等经典且广泛适用的模型上取得较好的分类结果,设计了本实验,选择的数据集为猫、狗数据集,它是kaggle上经典的图像二分类竞赛数据集,实验时猫、狗各选择2 000张作为基础数据集,按8∶2划分训练集、测试集。训练、测试时,输入图像尺寸为256×256像素,不做图像增强,Batch设置为64,采用随机梯度下降优化器,学习率为0.001,动量设置为0.9,采用交叉熵损失函数,Sobel池化、Mam池化中的α、β均设置为0.5。评价标准为充分训练后在测试集上的最高准确率,为降低偶然性,将测试集前五准确率均值也作为评价指标之一。
如表1所示,将VGG、ResNet等经典模型的池化层替换成Mam池化层后,Mam池化整体上优于平均池化,但并不优于最大池化,虽然Mam池化算法实现了对不同池化窗口进行划分,但并没有考虑特征图整体的内容、风格特征分布,因而效果并没有达到预期。
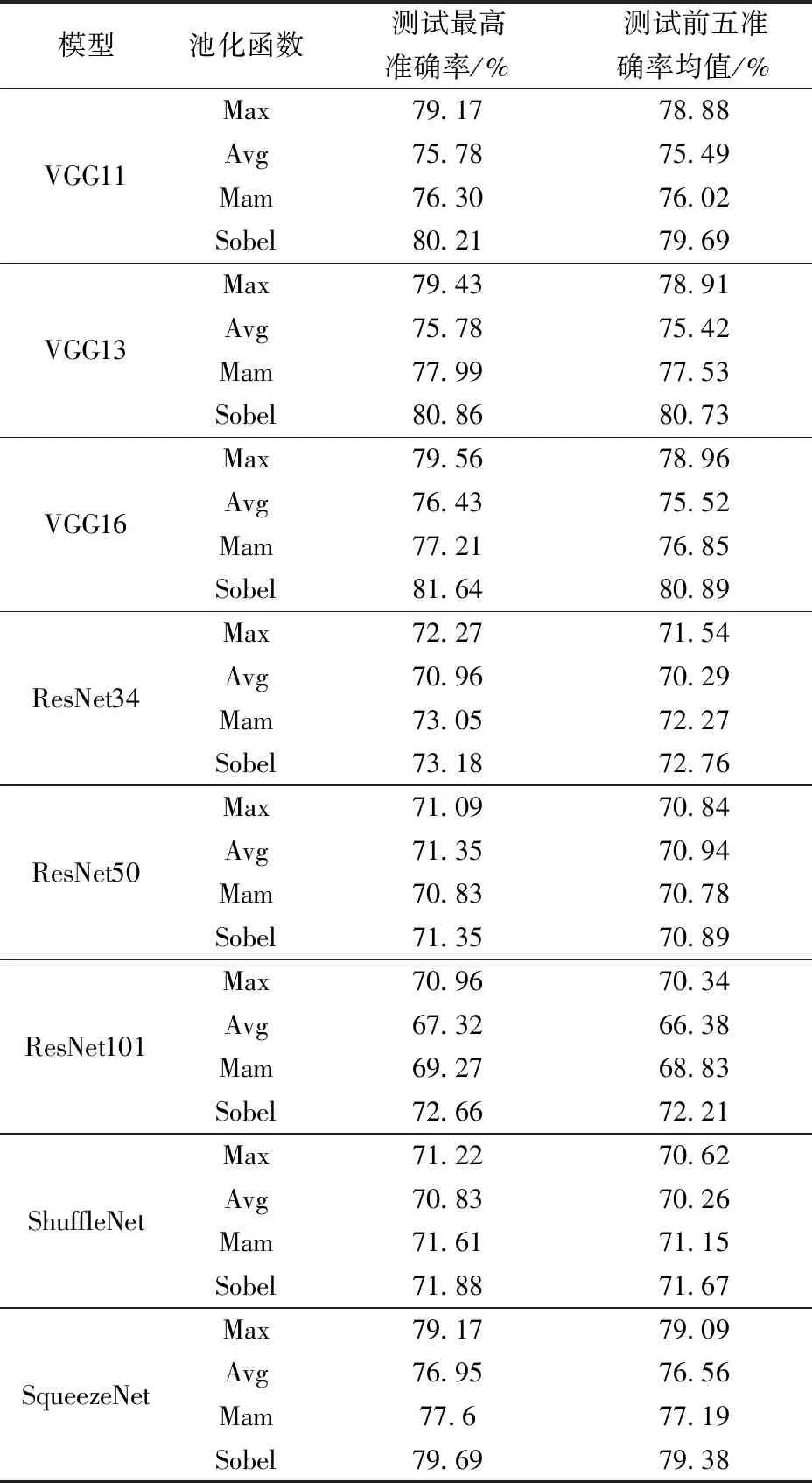
表1 各经典图像分类模型准确率Table 1 Accuracy of each classic image classification model
将池化层替换成本文设计的Sobel池化算法后,在测试集的准确率上有明显提升,均优于最大池化、平均池化、Mam池化,这也证实了Sobel池化算法能够替代常用的最大池化、平均池化,适用于各种卷积神经网络模型。
2.3 VGG16、Resnet34在不同数据集上的表现
本节实验选择的是广泛应用于图像分类、目标检测定位、图像分割等任务的基础VGG16模型以及Resnet34模型,所选择的数据集为Caltech101、Flowers数据集和Fruits360数据集[30]。Caltech101是用于图像分类、目标识别的数据集,包含101个种类,每种类别图像数量在40~800张不等,图像大小约为300×200像素。Flowers数据集是网上公开数据集,它包括雏菊、蒲公英、玫瑰、向日葵、郁金香5个种类,共计4 326张图像。Fruits 360数据集包含蔬菜、水果共计131个种类类,90 483张图片,图像大小为100×100像素。
如表2所示,本文所设计的Sobel池化算法不仅能够适用于不同经典模型,对同一模型在不同尺寸大小、不同数据量的图像数据集上亦能取得显著的提升,测试集上准确率均高于常用的最大池化、平均池化以及Mam池化,再一次证实了Sobel池化算法的具有较强的泛化性,适用于不同模型、不同数据集。
2.4 α、β超参数探索
Sobel池化中参数α、β的设定影响着模型准确率,根据式(7)知,当mG+αsG
如表3所示,根据实验结果可以看出,在一定范围内,随α、β取值的增大,准确率程下降趋势。随着(α+β)sG接近Gmax-Gmin时,Sobel池化测试准确率也在逐渐接近平均池化准确率。

表3 不同α、β取值下VGG16测试准确率Table 3 Accuracy of VGG16 under different α and β values
2.5 结果分析
根据上述实验结果可以看出,用本文设计的Sobel池化算法替换VGG、ResNet等经典模型中的池化层,经模型充分拟合训练集数据后,在测试集上的准确率均高于最大池化、平均池化以及简单的对激活后特征图求均值、标准差后分层的Mam池化,此外,Sobel池化算法在不同复杂数据集上亦取得了显著的提高,这证实了Sobel池化算法具有普适性、通用性,能够增强模型的泛化能力,稳定提高模型准确率。
3 结论
本文设计了一种基于Sobel算子的池化算法,将其命名为Sobel池化。Sobel池化先用Sobel算子对激活后特征图进行边缘检测得到梯度值,根据梯度变化明显点的分布,对特征图不同池化窗口进行选择性池化,这样能够在减少参数量的同时,尽可能的保留关键特征,降低信息损失,由于对特征图中的数据不只保留最大值或加权均值,而是根据特征图内容、风格分布综合决定每一个池化窗口选择最大值、平均值还是最小值作为池化结果,能够合理的保留背景、纹理等关键特征信息,有效的避免过拟合,稳定提升模型准确率。
通过实验可以明显看出本文设计的Sobel池化算法具有普适性、通用性,能够在不同的卷积神经网络模型、不同复杂数据集上取得较好的效果,可以用来替代常用的最大池化、平均池化。
