车铣复合数控机床空间误差建模和补偿
2024-01-16孟晓华于大国
孟晓华,于大国
(1.山西机电职业技术学院,山西长治 046011;2.中北大学机械工程学院,山西太原 030051)
0 前言
复合化、多功能数控机床的相关技术在不断更新,目前,这种机床的市场份额一直在增加,种类也一直在变化,在未来,这种机床占据的市场份额可能达到2/3。制造行业的发展方向细分化使该行业的个性化需求增多,因此,能够个性化、小批量生产的机床具备十足的发展潜力[1]。如何适应现代市场对个性化、多品种、低成本、小批量零件高效生产的需求是这种中小型机床目前必须要解决的问题,其关键就在于对自身性能的高要求、严标准[2]。机床自身的部件与结构对其加工性能的好坏有着直接的影响,确保其空间误差较低是保障零件加工效率与加工质量的前提。然而目前中小车铣复合数控机床的部件质量参差不齐,尤其是主轴部件,在性能与结构上都存在一定问题,因此机床普遍存在一定的空间误差,对其进行建模与补偿是解决该问题最简单的方法,因此对该问题进行研究。
对于数控机床来说,空间误差的建模与补偿问题一直是一个研究热点,很多学者都进行过该问题的研究。其中文献[3]提出一种基于灵敏度分析的建模与补偿技术,主要是通过切比雪夫多项式与关键误差元素的测量数据实现空间误差补偿模型的构建,并开发实时误差补偿系统。文献[4]提出一种精密卧式加工中心的误差建模、测量与补偿方法,主要是根据三维误差建模结果进行测量与补偿,提高了机床的空间定位精度。由于上述方法在车铣复合数控机床的应用中存在定位精度提升效果不好的问题,对此,设计一种车铣复合数控机床空间误差建模和补偿方法。
1 空间误差建模和补偿方法设计
1.1 几何误差辨识
针对车铣复合数控机床的两个旋转轴,忽略两轴位置的无关误差,通过齐次坐标变换理论分别构建其几何误差辨识模型,并对测试进行优化,实现两轴的几何误差辨识[5]。
用C轴表示旋转轴中的车削主轴,其误差辨识模型的构建过程具体如下:
(1)在测试前需要对直线轴误差进行补偿,以提升测试精度;
(2)在工作台上夹装一个球杆仪,用a表示工作台端球,b表示主轴端球;
(3)d表示球a与工作台端面之间的Z向高度,f表示其与C轴轴线的实际距离;
(4)使球杆仪与Z轴轴线平行,启动球杆仪的RTCP功能,并持续转动C轴,对球杆仪此时Z向的伸长量变化进行记录;
(5)以齐次坐标变换理论为依据,工件坐标系中球a的理想位置ai可以用下式来表示:
(1)
工件坐标系中球a的实际位置aj可以用下式来表示:
(2)
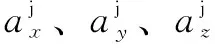
启动RTCP功能后,在C轴转动时,主轴端球b相对于C轴的位置几乎不变,而球a的实际位置与其理想位置间的差值如下式:
(3)
由于此时球杆仪与Z轴轴线是平行的,可以认为上式中Z轴轴线方向上球a的位置变动与球杆仪的伸缩量相等,如果在工件坐标系中改变球a的位置:a1(f1,d1)、a2(f2,d2)、a3(f3,d3),并使球杆仪与X、Y、Z轴线分别平行,能够获取以下方程组:
(4)

将上式展开,初步完成C轴误差辨识模型的构建:

(5)
通过对该误差模型进行求解,可以获得C轴的6项几何误差。以方程组解之间的存在性关系为依据,可知存在唯一解需要满足未知数个数与矩阵的秩相等的条件,因此可以将构建的C轴误差辨识模型简化,也就是对测试进行优化,直接省略a3(f3,d3)处的X、Y向测试与a2(f2,d2)处的Y向测试[9]。优化后的C轴误差测试流程具体如下:
(1)a1(f1,d1)处的X、Y、Z向测试;
(2)a2(f2,d2)处的X、Z向测试;
(3)a3(f3,d3)处的Z向测试。
通过以上步骤完成C轴最终误差辨识模型的构建,实现C轴的几何误差辨识[10]。
用B轴表示另一个旋转轴,通过同样的方法建模,实现其几何误差辨识,表达式为
(6)
1.2 空间误差模型构建
在工件坐标系下,根据旋转轴几何误差辨识结果,采用多体理论构建机床空间误差模型[11]。
空间误差模型的构建步骤如下:
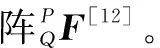
基于多体系统理论,将机床各体之间的运动变化等效转换为相邻随动坐标系之间的运动变换。在误差综合影响下,以P变换至Q的X轴坐标系为例,可以将这种运动变换分解为以下4种形式:
(7)
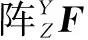
(8)
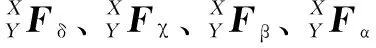
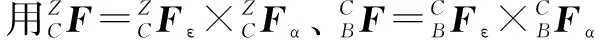
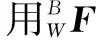
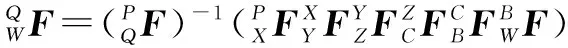
(9)
用实际刀尖点位置减去其理想位置,即可获取空间误差模型,具体如下式:
(10)
式(10)中:X、Y、Z表示三轴上的坐标值。
就此完成空间误差模型构建。
1.3 补偿策略设计
基于理想状态的逆运动学设计同步空间误差补偿策略,通过迭代方式对各轴补偿值进行计算,实现空间误差的补偿。该策略的具体运行流程如下:
(1)启动NC加工程序;
(2)通过下式表示各轴运动量,也就是各轴的机械坐标:
K=[X′,Y′,Z′,φ,φ]
(11)
式(11)中:X′、Y′、Z′、φ、φ分别表示X轴、Y轴、Z轴、B轴、C轴上的运动量。
(3)对各轴运动量进行更新,具体如下式:
K′=K+ΔK
(12)
式(12)中:ΔK表示更新的各轴运动量;K′表示更新后的各轴运动量[15]。K′的初始值为K′=K,ΔK=0。
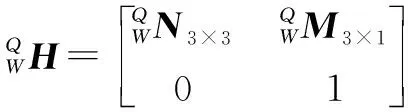
(13)
根据上式获取刀具的理想位姿,用(ωi,ξi)来表示。并根据存在几何误差的正运动学式计算此时转动链的变换矩阵,根据该矩阵获得刀具的预测位姿,用(ωj,ξj)来表示[17]。
(4)根据(ωi,ξi)和(ωj,ξj)计算此时的残留空间误差,当残留的空间误差比允许公差小,各轴补偿值具体如下式:
Kc=K′-K=[ΔX′,ΔY′,ΔZ′,Δφ,Δφ]
(14)
式(14)中:ΔX′、ΔY′、ΔZ′、Δφ、Δφ分别表示X轴、Y轴、Z轴、B轴、C轴上的运动补偿量[18]。
当残留的空间误差比允许公差大,根据理想逆运动学思想,求取各轴的运动量,并将其作为各轴的补偿值。首先在理想状态下机床的逆运动学求解过程中代入[Δω,Δξ′]所对应的位姿增量,获取其运动学逆解。其中Δω表示理想位姿的偏差;Δξ′表示实际位姿的偏差的单位向量。获取的运动学逆解为ΔK1=[ΔX′1,ΔY′1,ΔZ′1,Δφ1,Δφ1]。在之前的运动量上叠加ΔK1,此时刀具实际运动姿态用P1来表示,计算P1处的运动量。此时相比理想位置,P1处产生一组新误差[19]。不断重复以上过程,使刀具逐渐接近理想位姿,并不断对该过程中的运动量进行计算,叠加所计算的运动量,完成各轴运动量的求取,作为各轴的补偿值[20]。
2 实验测试
2.1 机床参数
为证明设计的车铣复合数控机床空间误差建模和补偿方法的有效性,以一台车铣复合数控机床为研究对象,对该机床实施空间误差建模和补偿。实验机床各轴的行程与定位精度如表1所示。

表1 实验机床具体参数Tab.1 Specific parameters of the experimental machine tool
2.2 实验准备
实验中的坐标系设置情况如表2所示。

表2 坐标系具体参数Tab.2 Specific parameters of coordinate system
2.3 实验方法设计
实施旋转轴的几何误差辨识。在辨识前首先对直线轴误差进行补偿,补偿方式为校正机床机械零点。具体校正步骤如下:
(1)通过压表法寻找Z轴轴线与B轴轴线平行时的角度,将其设置为-90°;
(2)寻找检棒平行于Y轴、X轴的4个高点;
(3)调整Y轴、X轴的坐标,使C轴与检棒同心;
(4)将Y轴、X轴此时的机械坐标置零;
(5)使B轴返回0°,将刀仪与工件主轴端面靠近,考虑检棒半径与对刀仪距离,将机械坐标零点直接设置在工件主轴端面与刀具主轴轴线对齐的位置。
构建的C轴和B轴几何误差辨识模型如公式(5)和公式(6)所示,接着构建其空间误差模型,并通过同步空间误差补偿策略进行空间误差补偿,根据补偿结果测试各轴的定位精度及其重复定位精度,并对机床进行圆锥体的误差补偿测试,对其测量结果进行分析,观察设计方法的直观误差补偿效果。
在测试中,为形成对比效果,将基于灵敏度分析的建模与补偿技术与精密卧式加工中心的误差建模、测量与补偿方法作为对比方法,共同进行实验。用方法1、方法2表示这两种方法,使叙述更加简洁。
2.4 定位精度测试
首先测试3种方法补偿后机床各轴的定位精度,观测3种方法各轴的定位精度相较于原本定位精度的变化情况,测试结果如图1所示。
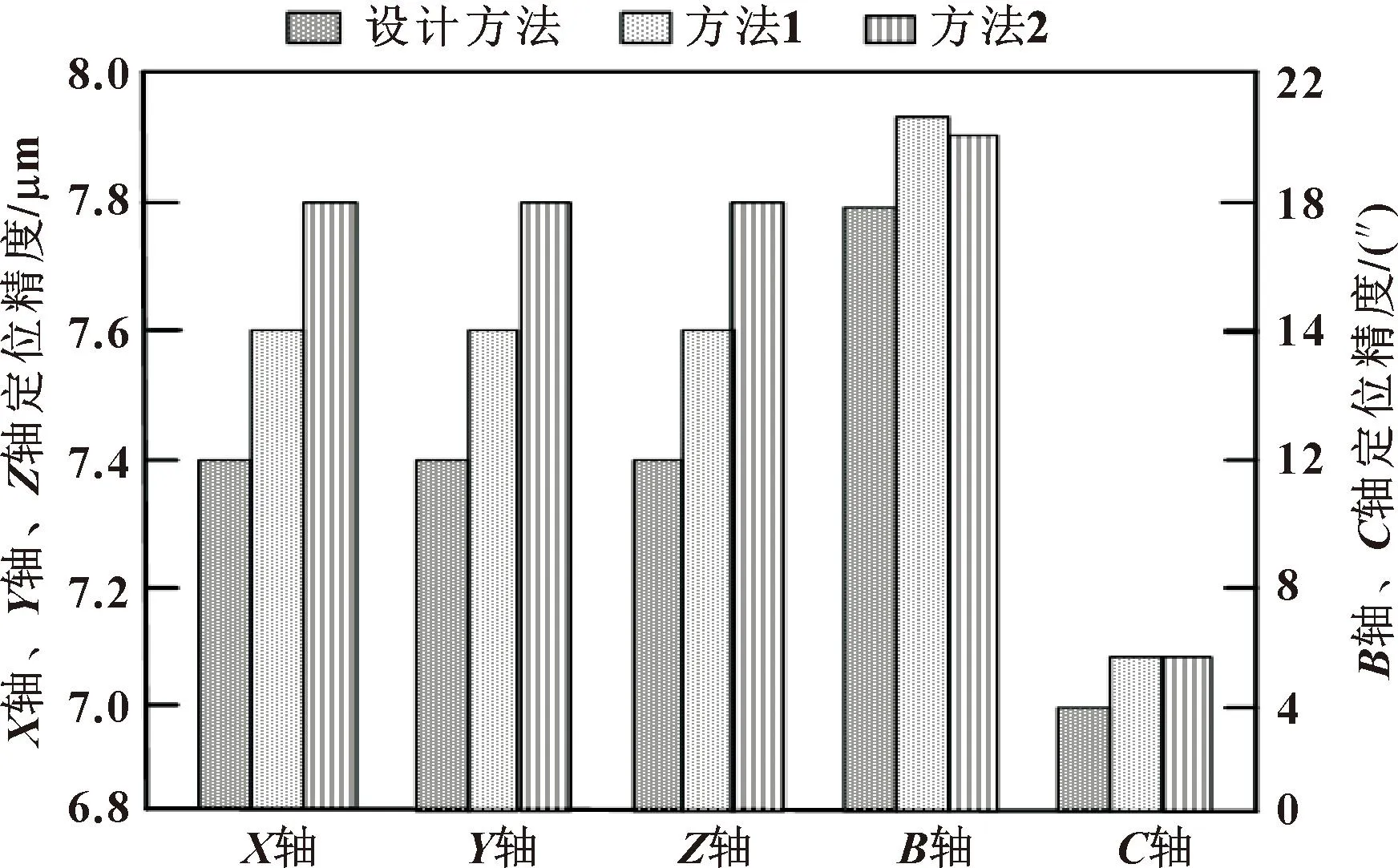
图1 各轴的定位精度测试结果Fig.1 Positioning accuracy test results for each axis
由图1可以得出:文中方法补偿后,实验机床X轴、Y轴、Z轴的定位精度相比原本的定位精度提升了0.6 μm,B轴的定位精度提升了4″,C轴的定位精度提升了3″;方法1补偿后,实验机床X轴、Y轴、Z轴的定位精度相比原本的定位精度提升了0.4 μm,B轴的定位精度提升了1″,C轴的定位精度提升了1″;方法2补偿后,实验机床X轴、Y轴、Z轴的定位精度相比原本的定位精度提升了0.2 μm,B轴的定位精度提升了2″,C轴的定位精度提升了1″。对比可知,文中方法能够实现最大程度的定位精度提升。
2.5 重复定位精度测试
接着测试3种方法补偿后机床各轴的重复定位精度,观测3种方法各轴的重复定位精度相较于原本重复定位精度的变化情况,测试结果如图2所示。
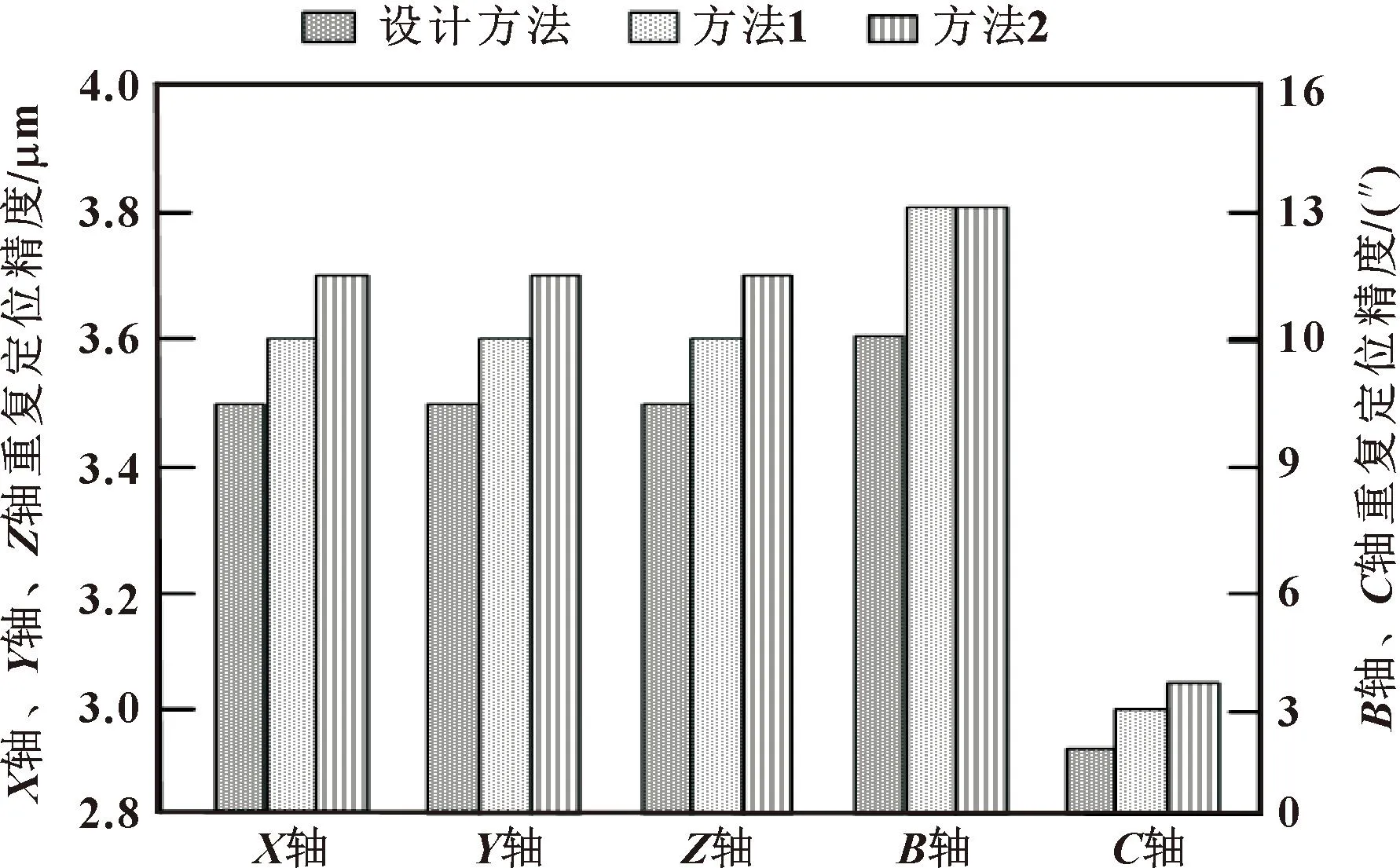
图2 各轴的重复定位精度测试结果Fig.2 Repetitive positioning accuracy test results for each axis
图2表明:文中方法补偿后,实验机床X轴、Y轴、Z轴的重复定位精度相比原本的重复定位精度提升了0.5 μm,B轴的重复定位精度提升了6″,C轴的重复定位精度提升了3″;方法1补偿后,实验机床X轴、Y轴、Z轴的重复定位精度相比原本的重复定位精度提升了0.4 μm,B轴的重复定位精度提升了3″,C轴的重复定位精度提升了1″;方法2补偿后,实验机床X轴、Y轴、Z轴的重复定位精度相比原本的重复定位精度提升了0.3 μm,B轴的重复定位精度提升了3″,C轴的重复定位精度提升了1″。经过对比,设计方法能够最大程度上提升重复定位的精度。
2.6 圆锥体的误差补偿测试
对补偿后的实验机床进行圆锥体的误差补偿测试,主要是对正反行程中反行程产生的误差进行测试,以获得更加直观的误差补偿效果。共进行3次实验,每次正反行程的半径不同,分别测试半径较大、居中、偏小的圆度情况。
半径较大时,反行程的实验圆度如图3所示。
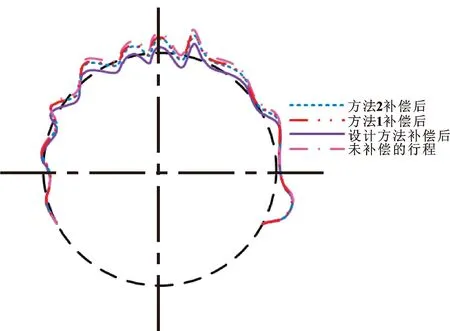
图3 半径较大的测试情况Fig.3 Test cases with larger radii
根据图3,半径较大时,经过方法1、方法2的补偿后,反行程的实验圆度得到了一定降低,而经过设计方法的补偿后,设计方法反行程实验圆度比方法1、2好,说明设计方法的误差补偿效果更好。
半径居中时,反行程的实验圆度如图4所示。
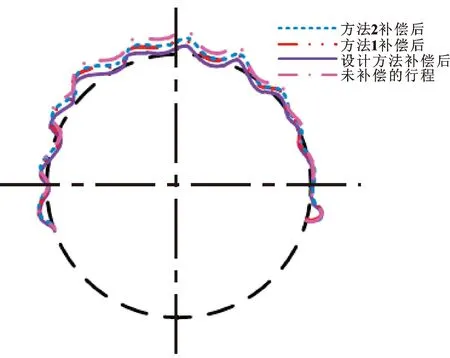
图4 半径居中时的测试情况Fig.4 Test situation when the radius is centered
图4表明:半径居中时,经过方法1、方法2的补偿后,反行程的实验圆度得到了一定降低;而经过设计方法的补偿后,反行程实验圆度的降低幅度比方法1、方法2大,同样能够证明设计方法的误差补偿效果更好。但整体来看,3种方法的降幅都比半径较大时小。
半径偏小时,反行程的实验圆度如图5所示。
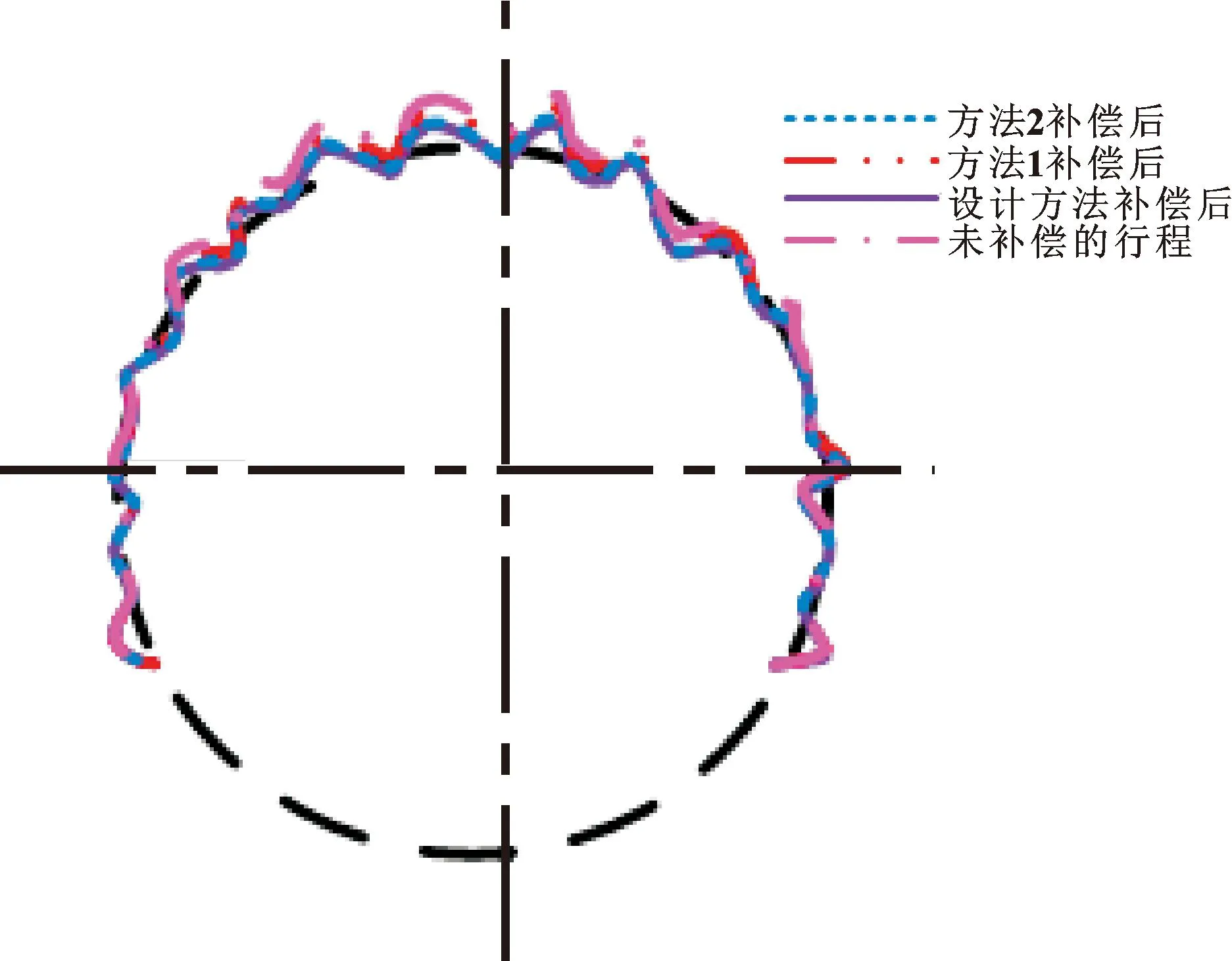
图5 半径偏小时的测试情况Fig.5 Test situation with small radius deviation
图5表明:半径偏小时,同样是设计方法的圆度降幅大于方法1、方法2。但半径偏小时3种方法的整体降幅在3种半径情况中最小,说明行程半径越大,能够实现的误差补偿部分越大,反之,能够实现的误差补偿部分越小。
3 结束语
针对车铣复合数控机床进行系统性研究,提出一种空间误差建模和补偿方法,实现了误差的离线补偿,提升了机床的柔性加工制造与灵活的误差补偿,解决了目前的方法存在的局限性,对于中小车铣复合数控机床的精细化发展有意义。
