轴流式止回阀缓冲结构参数对止回性能的影响

张立强，刘岱阳

(兰州理工大学能源与动力工程学院，甘肃兰州 730050)

0 前言

轴流式止回阀具有启闭迅速、正向流阻低等特点，通常安装在长输管线以及泵站的出口位置，以防止介质倒流以及反向水锤对管线和泵站的破坏。

近年来，随着国内阀门制造的步伐逐渐加快，对于轴流式止回阀的研究也逐渐深入。冯明、吴业飞[1]对轴流式止回阀的阀瓣以及阀体喉部进行优化设计，确定了最小流阻的收缩因数为80%。黄昕珂等[2]通过模拟水泵停电后的回流过程，验证了轴流式止回阀优异的抗水锤性能。周强强等[3]针对核电站主给水管线破裂事故引起的水锤效应，采用数值仿真的方式，验证了带有缓冲装置轴流式止回阀的优势。张希恒等[4]应用Fluent动网格技术对阀瓣闭合过程中的加速度以及阀座受力情况进行分析，得出了阀门内部流场的变化情况。WANG等[5]采用显示动力学对止回阀关闭过程中阀瓣对阀座的冲击进行模拟，得到了阀瓣的响应速度及阀门闭合过程中的能量变化情况。张娜等人[6]对轴流式止回阀的止回过程进行仿真，分析了阀瓣闭合过程中的应力变化情况。王廷[7]根据离心泵的工作特性曲线，结合C语言编写的阀瓣驱动程序，对阀瓣的闭合过程进行了分析。王秋林等[8]针对阀门实际尺寸较大而无法实验的情况，利用流动相似原理对模型进行缩小，在保证结果正确的前提下简化了实验过程。

在上述研究的基础上，为了提升止回阀止回过程的抗水锤能力，本文作者对原有的笛形缓冲结构进行改进，该缓冲装置可以保证阀瓣在反向止回过程中实现快关缓闭，从而最大程度地降低阀瓣对阀体的冲击[9-11]。同时，针对改进后缓冲装置的结构参数进行正交试验，并进行极差分析，最终对影响阀门闭合速度、瞬态液动力的因素进行权重排序。

1 轴流式止回阀的工作原理

图1所示为轴流式止回阀的结构示意，它由阀芯和阀体两部分组成，其中阀芯包含阀瓣、导流罩、阀杆、阀套以及弹簧等。

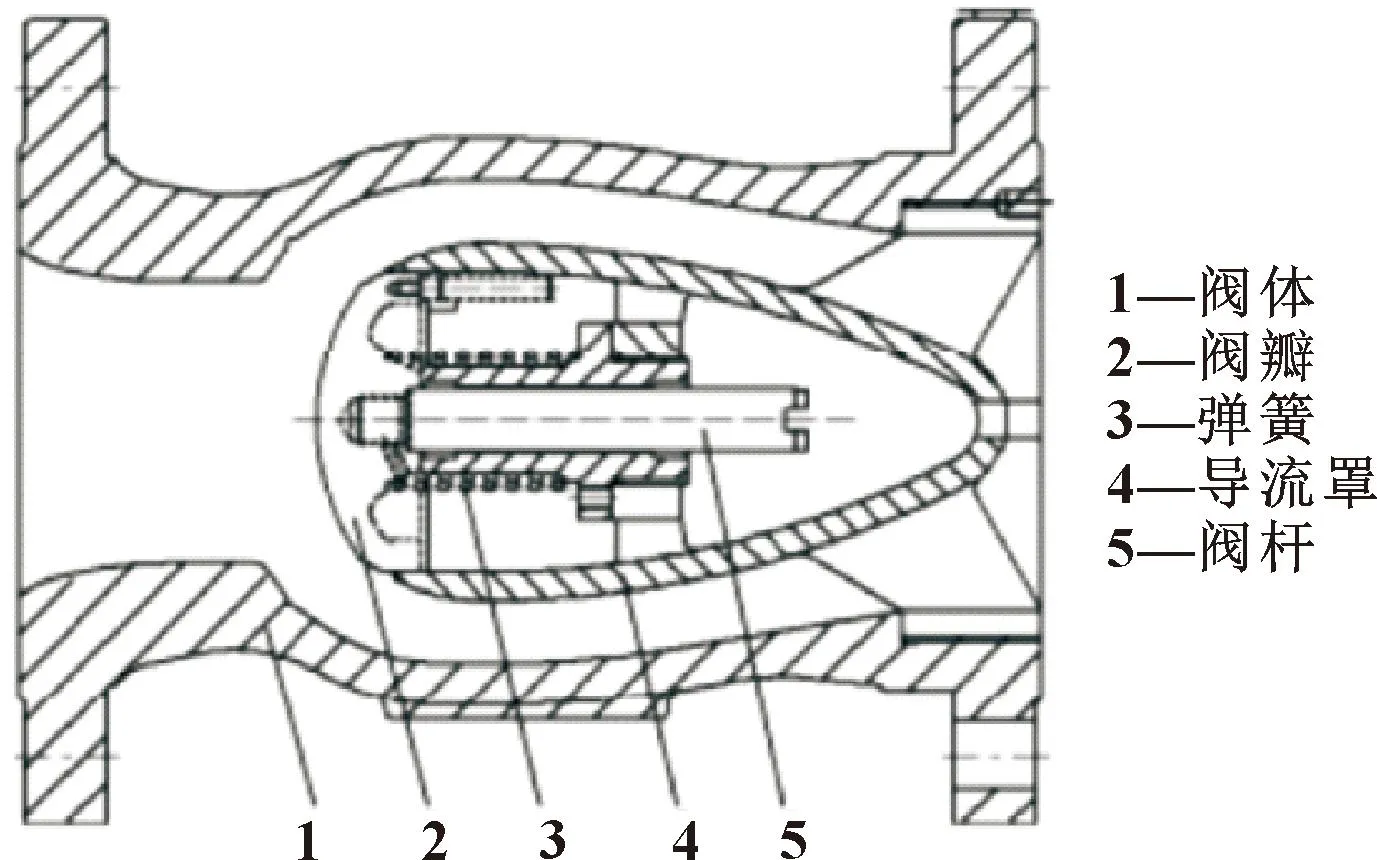
图1 轴流式止回阀内部结构示意Fig.1 Internal structure schematic of axial flow check valve

其工作原理为：当正向来流从左向右通过止回阀时，阀瓣在前后压差以及正向来流冲击的作用下从左向右运动，实现阀门的开启；当反向水锤从右向左进入止回阀时，阀瓣在反向水锤和弹簧力的共同作用下从右向左运动，实现阀门的闭合。

2 缓冲结构的工作原理

图2所示为缓冲结构示意。在止回阀阀杆的尾部增加一个液压缓冲缸和活塞。止回时，在水锤的推动下，缓冲活塞带动阀杆以及阀瓣向左运动，实现阀门的闭合，而当缓冲活塞进入到液压缸内部时，高速运动的活塞会对液压缸内的流体介质进行压缩，流体介质通过活塞与液压缸壁间的缝隙以及阻尼孔排出，并对活塞产生反向阻尼作用，实现阀门的两阶段“快关缓闭”，起到保护阀门的作用[12]。

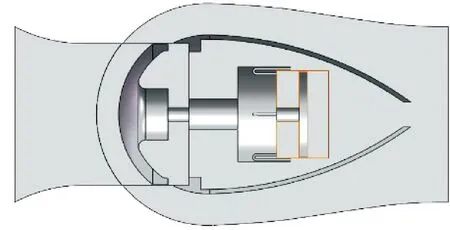
图2 改进缓冲结构示意Fig.2 Schematic of the improved buffer structure

决定阀瓣止回过程中缓冲性能的结构参数包括：活塞直径、活塞行程、阻尼孔直径、阻尼孔个数、环缝间隙大小等。将阻尼孔开在阀套的端盖上，阻尼孔的通孔面积不会因活塞的运动而发生变化，因此在止回过程中缓冲装置的阻尼呈现线性。除此之外，将阻尼孔的结构设计为U形，可以改变液压缸内被压缩流体的流动方向，抵消一部分反向水锤的冲击，从而达到提升止回性能的目的。

3 数值试验

3.1 三维模型的建立以及前处理

对轴流式止回阀阀芯的不同缓冲结构验证，需要采用动网格技术进行数值试验，文中对PumpLinx动网格中的滑阀模板进行仿真。需要注意的是，由于PumpLinx中需要定义阀芯弹簧的压缩反向以及阀芯的初始位置，为了模拟出真实情况下轴流式止回阀阀芯的止回过程，需要对阀门启闭的一个周期进行数值试验。

此外，使用PumpLinx对止回阀进行数值试验，需要提前将阀体的内部流道结构的三维模型抽取出来，并且需要划分不同的网格区域，即将阀芯的移动区域与固定区域进行切分。并且在局部区域需要进行网格的细化处理，以避免因网格重叠导致试验失败。具体将整个流道区域划分为4个部分：阀门进口、阀瓣运动区域、缓冲结构的运动区域以及阀门出口区域。具体的流道模型如图3所示。

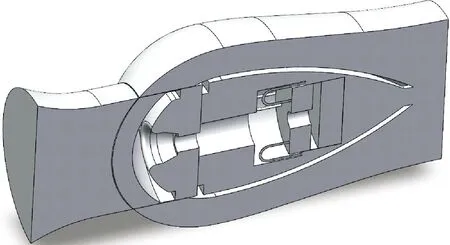
图3 流道模型三维结构Fig.3 The 3D structure of flow channel model

在PumpLinx中，使用General Mesher对阀门的进、出口区域进行网格划分，最大体积网格单元尺寸为0.005 mm。对阀瓣以及缓冲结构的移动区域采用Valve Template Mesher进行动网格区域的划分，最大网格单元尺寸为0.001 mm。此外，还需要在划分之前指定阀芯表面、压缩面以及阀芯位移的起始和终止面。最终生成的网格如图4所示。

图4 网格划分示意Fig.4 Schematic of grid division

3.2 缓冲装置的阻尼孔结构验证

笛形缓冲结构的阻尼孔开在液压缸侧壁上，这种结构的优点是加工容易、简单可靠，同时抗污染能力较强，较小的颗粒污染物也不容易堵塞。但是其缺点是：当活塞进入到液压缸内时，阻尼孔的通流面积会随活塞的位移变化而减小，造成流量减少，从而导致缓冲阻尼突然增加，最终使得阀芯内部的瞬态液动力发生突变，产生振动。

因此，改变笛形缓冲装置的节流孔位置，在液压缸的端盖位置开孔，可以保证阻尼孔的通流面积不随缓冲活塞的位移而发生改变，从而最大限度地保证缓冲过程中阻尼的线性度[13]。

对2种不同缓冲结构的缓冲效果进行数值验证，以长度333 mm、质量136 kg、弹簧刚度2 730 N/m、通径252 mm的轴流式止回阀作为试验对象，验证方式选择PumpLinx软件对止回阀的闭合过程进行动态数值模拟。首先，在SolidWorks中建立止回阀的2种内部流场结构，分别如图2和图5所示。其次，将其保存为“.STL”格式，并导入到PumpLinx中，通过计算阀门闭合过程中最大的瞬态液动力判断不同缓冲装置的线性程度。以100 m扬程的实际工况为例，进行试验对比分析[14]。在实际工况中，当阀门前端管线出现破裂或者泵站突然停电时，阀门入口压力会突然降低至标准大气压。经过计算，阀门出口的压力可以达到981 000 Pa，为了试验方便，近似为1 MPa。此外，通过正向阀门的开启试验，已经初步验证进口压力为10 MPa、出口压力为5 MPa时，阀门的正向开启时间为0.01 s，因此采用变进口压力函数、定出口压力函数的方法设定边界条件[15]。进口压力函数如式(1)所示：

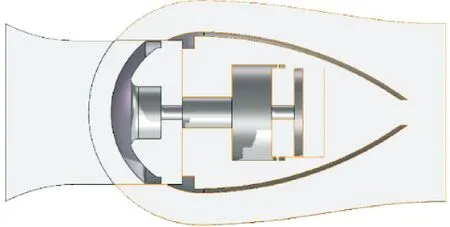
图5 笛形缓冲结构示意Fig.5 Schematic of flute buffer structure

(1)

保持出口压力1 MPa不变，对2种不同模型的试验结果进行对比分析。图6所示为安装改进缓冲结构止回阀的阀瓣在一个启闭周期内的位移曲线，阀瓣完全闭合的时间为0.038 6 s，并且在闭合的过程中，分为2个阶段。以0.030 7 s为分界点，止回的前半部分为缓冲活塞在反向水锤冲击下自由运动的阶段；而在0.030 7 s到阀瓣完全闭合的第二阶段，缓冲活塞进入液压缸，受到反向阻力，因此位移曲线斜率发生了较大变化。

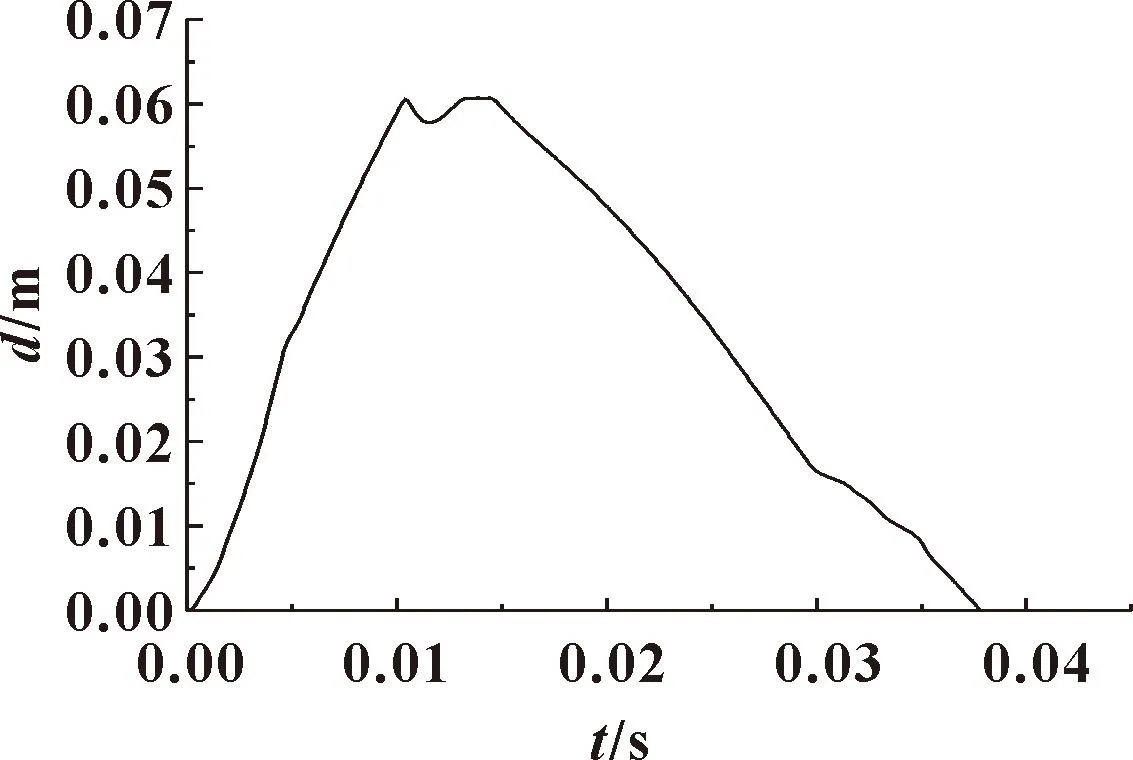
图6 改进缓冲结构阀瓣位移Fig.6 Disc displacement of improved buffer structure

图7所示为安装传统笛形缓冲装置止回阀的阀瓣启闭过程位移图像。可以看出：阀瓣在止回过程中的位移图像同样分为2个阶段，不同的是，在止回过程的第二阶段，即0.035 2 s处，阀瓣位移突然出现了短暂的反向运动，并且阀瓣的反向闭合时间延长，由原来的0.038 6 s延长至0.039 2 s，延长了0.000 6 s。这是因为与改进缓冲结构相比，笛形缓冲结构的阻尼孔面积会受到活塞移动的影响，随着阀门开度逐渐减小，缓冲活塞也逐渐靠近液压缸的端盖。随着位移的增加，对笛形阻尼孔面积的遮挡也逐渐增大，因此液压缸内的流体介质只能通过环缝间隙排出，从而增加了缓冲活塞的阻尼，才出现了反向运动。

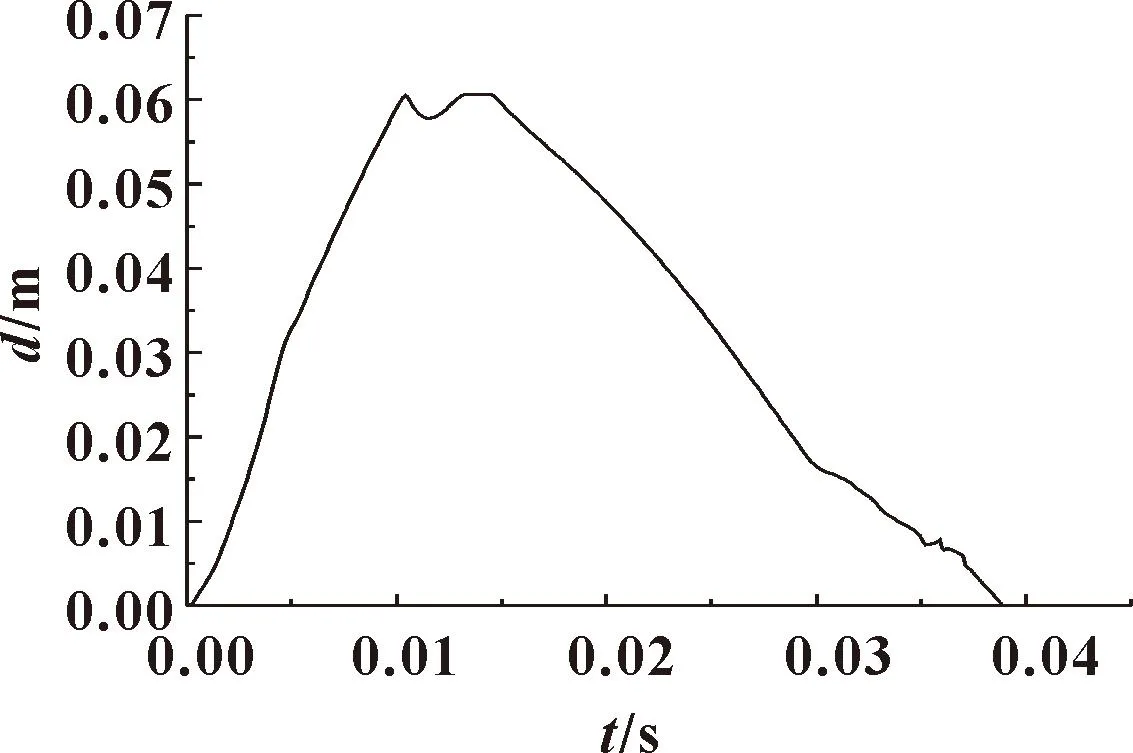
图7 笛形缓冲结构阀瓣位移Fig.7 Disc displacement of flute buffer structure

图8和图9所示分别为2种不同缓冲装置在阀瓣一个启闭周期内的瞬态液动力曲线。可以看出：2种缓冲装置间的最大区别发生在0.038 3 s以后，改进缓冲装置的瞬态液动力保持在50 000 N左右，而传统笛形缓冲装置的瞬态液动力则始终保持在120 000 N左右。

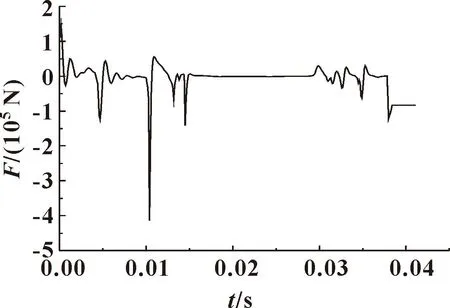
图9 笛形缓冲结构的瞬态液动力Fig.9 Transient fluid power of the flute buffer structure

这是由于活塞移动一定的行程后将阻尼孔堵塞，使得被压缩的流体介质只能通过环缝排出液压缸，从而使得缓冲阻尼瞬间增加，形成较大的瞬态液动力。相比之下，改进缓冲结构不受液压缸活塞运动的影响，在阀瓣闭合的后段瞬态液动力总体较小，因此整体缓冲过程更趋于线性，引起的阀芯振动也相对较小[16]。

3.3 结构参数的选取及正交试验

分析影响缓冲性能的结构参数，需要设计正交试验，以保证其试验结果均匀分布、整齐可比[17-18]。具体选取的结构参数为液压缓冲缸的行程、缓冲活塞直径以及阻尼孔的直径。各个结构参数对应的水平选取范围分别为：液压缸缓冲行程为16.0～20.0 mm，缓冲活塞直径有效范围为119.0～121.0 mm，阻尼孔直径变化范围为2.5～3.5 mm。通过测量，长度333 mm、质量136 kg的轴流式止回阀阀瓣从全开到完全闭合的行程为45.74 mm。

液压缸缓冲行程水平均匀地选取3个，分别为16.0、18.0、20.0 mm；缓冲活塞直径共选取3个水平，依次为119.0、120.0、121.0 mm；阻尼孔直径的水平分布为2.5、3.0、3.5 mm。因此，对上述3个结构参数进行三因素五水平正交试验设计，总试验次数为9，正交试验方案如表1所示。

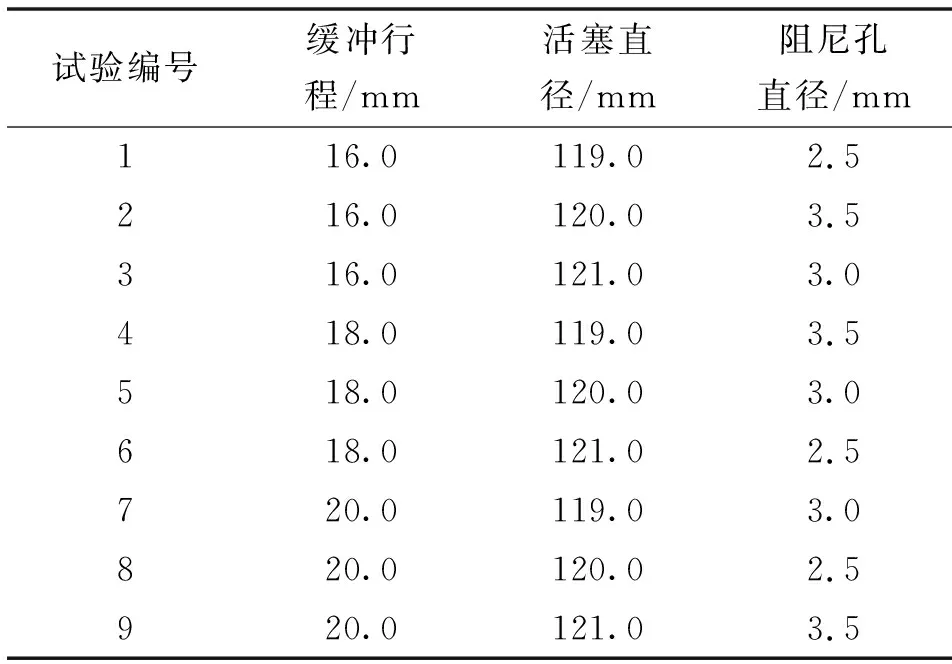
表1 止回阀缓冲结构参数正交试验方案Tab.1 Orthogonal test scheme of buffer structure parameters of check valve

针对上述9组模型，首先采用SolidWorks三维软件在流道区域进行建模，后续通过PumpLinx测试止回性能。测试的指标主要有2个：阀门的完全闭合时间以及止回过程中阀门的最大瞬态液动力。具体的试验结果如表2所示。

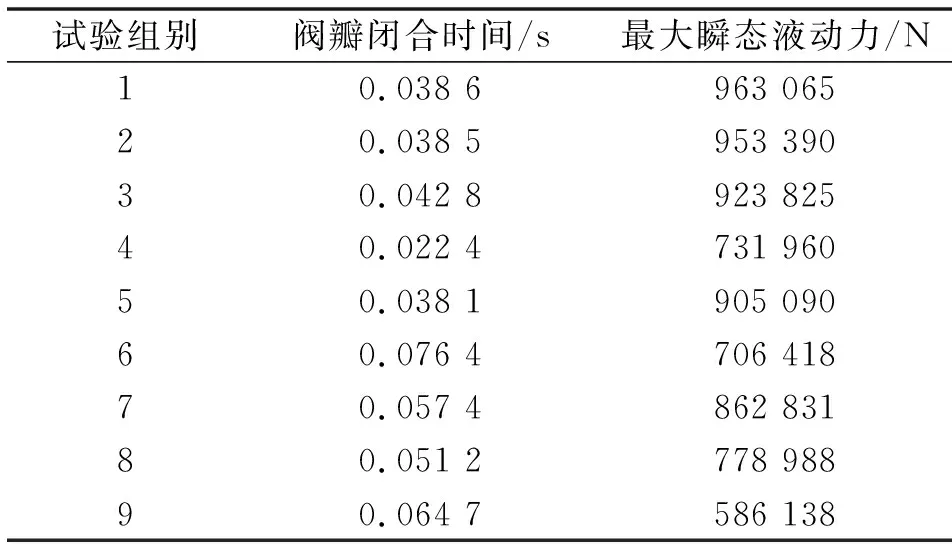
表2 正交试验结果Tab.2 Orthogonal test results

4 试验结果处理

4.1 极差分析

分析正交试验结果的极差，从而对影响阀门2个止回性能的结构参数进行权重排序。利用Excel表格计算极差，首先对阀瓣的闭合时间进行分析。通过计算可以得知：缓冲行程所对应的极差为0.017 8，活塞直径对应的极差为0.021 8，阻尼孔直径对应的极差为0.013 5。因此，结构参数对于阀瓣闭合时间的影响大小为：活塞直径>缓冲行程>阻尼孔直径。

同样，对最大瞬态液动力进行分析，活塞直径、缓冲行程以及阻尼孔直径对应的极差值分别为140 362、204 107和140 086，对最大液动力的影响因素排序为：缓冲行程>活塞直径>阻尼孔直径。

4.2 缓冲结构参数的多目标优化

对于轴流式止回阀的改进缓冲结构，增加缓冲阻尼以及降低止回过程中阀芯的振动是优化的2个主要目标。具体体现在延长阀瓣闭合时间的同时降低最大瞬态液动力。

使用均匀设计试验法，重新选取样本点进行数值试验。并将Kriging插值模型、RBF神经网络、响应面模型(RSM)以及正交多项式模型(OPM)与试验结果进行对比，最终以方差和的形式进行误差分析，如表3所示。

表3 不同代理模型的误差分析Tab.3 Error analysis of different agent models

从表3可知：拟合结果与实际测量值最接近的代理模型为响应面模型。因此，选用响应面模型对正交试验的样本点进行拟合。

使用响应面代理模型对正交试验的9个数值结果进行曲面插值，预测出全局结果，图10所示为活塞直径和缓冲行程对阀瓣闭合时间的影响趋势。

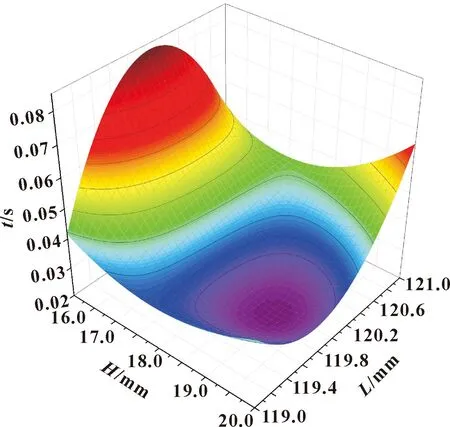
图10 活塞直径和缓冲行程对阀瓣闭合时间的影响趋势Fig.10 Influence of piston diameter and buffer stroke on disc closing time

同样，图11所示是活塞直径和缓冲行程对瞬态液动力的影响趋势。

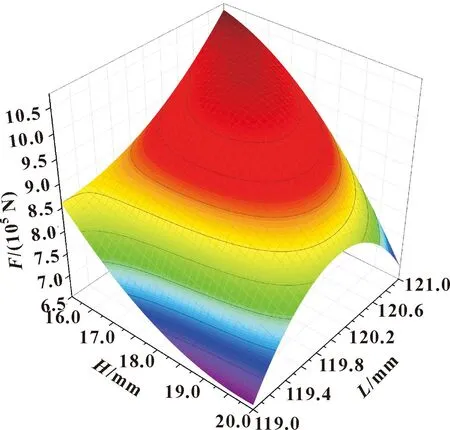
图11 活塞直径和缓冲行程对瞬态液动力的影响趋势Fig.11 Influence of piston diameter and buffer stroke on transient fluid power

最后，利用NSGA-II遗传算法[19]对全局寻得的最优结果进行多目标优化。并采用均值平方差的方法作为目标函数，具体如式(2)所示。

(2)

其中：s1(x)和s2(x)分别为阀瓣关闭时间的均方差以及瞬态液动力的均方差；p为总试验次数；t和F分别为每一种结构参数下对应的阀瓣闭合时间以及瞬态液动力；f(x)为实际工况下阀瓣闭合时间以及瞬态液动力随结构参数的变化函数。约束条件为：缓冲行程16.0～20.0 mm，活塞直径119.0～121.0 mm，阻尼孔直径为2.5～3.5 mm。此外，通过上述分析可知对于轴流式止回阀缓冲结构的要求是：在保证阀瓣闭合时间较小的前提下，尽可能地降低止回过程中阀芯的振动，即阀瓣闭合时间t以及瞬态液动力F都要尽可能小。

快速非支配排序遗传算法(NSGA-Ⅱ)是目前使用范围较广的遗传算法之一，其核心思想就是通过非支配排序以及拥挤度筛选出符合优化目标的种群，并且在最终的Pareto前沿中得到具有不同支配地位的可行优化解。在Isight的Optimization模块中，由Kriging代理模型得到全局解。设置初始种群数量为200，迭代次数为500步，最终得到的Pareto前沿如图12所示。

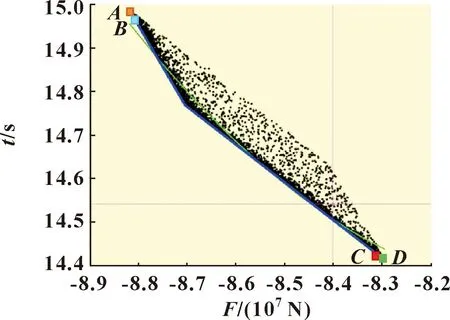
图12 多目标优化Pareto前沿Fig.12 Pareto front of multi-objective optimization

由图12可以看出：图像中的每一个点都是最终优化完成后的一个可行解。然而，对于改进缓冲结构的多目标优化[20]，被优化的2个目标具有对立性，即减小阀门止回时间的同时，阀芯的振动增大。因此，对于止回阀缓冲结构的多目标优化并不存在最优解，图12中位于曲线上的所有点为优化后的解集，针对不同的实际工况可以选取前沿上的最优解。

具体而言，图12中的点A表示止回过程中瞬态液动力最大而阀瓣闭合时间最长的工况，点D表示止回用时最短而瞬态液动力最小的工况。最终可以根据实际要求，在Pareto前沿(图12的蓝色曲线)上选取合适的最优解。点B与点A的最优解性能相似，一定程度上可以替代点A，而点A、B的实际结构尺寸却不相同，这意味着可以在降低加工精度的情况下使产品达到相同的性能。同理，点C与点D性能相同，但是两者的结构尺寸并不相同，因此降低了对加工精度的要求。

5 结论

文中基于轴流式止回阀的笛形缓冲结构得到了一种改进缓冲结构，并针对其止回性能进行数值试验，最后对试验结果进行优化。得到了以下结论：

(1)综合对比轴流式止回阀改进缓冲结构与传统笛形缓冲结构在100 m扬程工况下的止回性能可知：笛形缓冲结构由于受阻尼孔面积变化的影响，阀门闭合时间较改进缓冲结构增加了0.000 6 s。此外，在0.038 3 s以后，改进缓冲结构的瞬态液动力维持在50 000 N左右，低于传统笛形缓冲结构的120 000 N，有效地降低了止回过程中阀芯的振动，提高了阀门稳定性。

(2)通过对改进缓冲结构的参数进行正交试验，并通过极差对影响缓冲性能的结构参数进行权重排序可知：对于阀门止回时间的影响因素权重为：活塞直径>缓冲行程>阻尼孔直径；对于阀门止回最大瞬态液动力的影响因素权重为：缓冲行程>活塞直径>阻尼孔直径。

(3)通过Kriging插值进行正交试验结果的无偏估计以及NSGA-Ⅱ遗传算法的优化，可以得到最终的Pareto前沿。可以看出：2个被优化目标的最优解并不具有统一性，因此并不存在唯一的最优解，可以根据实际需求选取Pareto前沿上对应的最优结构参数。同时，由于每一个可行解的周围都有很多结构参数差异不大但性能相同的解，因此，在保证性能相同的前提下，可以通过适当降低加工精度的方式来节约制造成本。