互质阵MIMO雷达DOA估计性能综合分析

杨清亮, 王鸿帧,, 张宇乐, 陈 晨

(1.中国人民解放军93575部队,河北 承德 067000; 2.空军工程大学,西安 710000;3.中国人民解放军95980部队,湖北 襄阳 441000)

0 引言

波达方向(DOA)估计作为阵列信号处理的研究内容之一,在雷达、声呐、通信等军事和经济领域均有着广泛的应用[1-2]。空间谱估计测向技术可以不受阵列的物理孔径限(常称为瑞利限)的限制,分辨位于一个波束宽度内的空间目标,在不增大天线孔径的前提下,提高DOA估计精度[2-4]。多输入多输出(MIMO)雷达是把无线通信中的多输入多输出技术引入雷达领域,进而与数字阵列技术结合所产生的一种新型雷达[5-6]。MIMO雷达由于采用了波形分集技术,与传统阵列雷达相比具有抗干扰能力强、分辨率高、多目标跟踪能力强的优点[6]。

随着MIMO雷达概念被提出,研究者们开始关注并研究MIMO雷达的DOA估计方法,在MIMO雷达的基础上提出了许多新的、更有效的DOA估计方法[6]。文献[7-8]提出了基于MIMO雷达的多重信号分类(MUSIC)算法,较大地提升了DOA估计精度;为了估计相干目标来波方向,文献[9]提出了适用于MIMO雷达的空间平滑算法,该算法虽然具有不错的解相干能力,但一定程度上损失了阵列孔径;文献[10]针对极化 MIMO雷达特点,在不损失阵列孔径的前提下提出了一种加权极化平滑算法,该算法具有更高的DOA估计精度;文献[11-12]将最大似然算法应用于MIMO雷达,有效解决了米波MIMO雷达中低仰角估计中的多径问题;上述算法由于谱峰搜索计算复杂度较大,为了降低计算量,文献[13]将旋转不变子空间(ESPRIT)算法应用于MIMO雷达系统,有效地估计出信号的波达角,且运算量较小;文献[14-16]在保持一定DOA估计精度的前提下,通过实值和降维处理方法进一步降低了基于MIMO雷达的ESPRIT算法复杂度。

以上算法均采用均匀线阵(ULA)MIMO(ULA-MIMO)雷达信号模型,目前适用于均匀线阵MIMO雷达的DOA估计技术已较成熟[17-18]。现代战争具有敌空中目标数量多、间隔小等特点,促使目标探测需要更高的角度分辨力、测角精度及自由度[19]。均匀线阵MIMO雷达在自由度、测角精度和分辨力方面已满足不了现代战争的实际需求[19]。而互质阵(Co-Prime Array,CPA)[20-25]以其特有的高自由度、高分辨力、高精度、低互耦率和低开销等优势为解决这一问题提供了较为成熟的方案,且其巨大性能优势与MIMO雷达结合可构造和联合阵列(Sum Coarray,SCA)以及和差联合阵列(SDCA)[22]提升自由度和扩展虚拟阵列孔径,进而提升角度估计性能。基于此,本文结合MUSIC算法,根据单基地互质阵MIMO雷达特点,详细分析了基于和联合阵列及和差联合阵列的DOA估计方法,最后运用仿真实验与均匀线阵进行参数对比,验证了互质阵MIMO雷达测向性能的优越性。

1 互质阵MIMO雷达信号模型

1.1 阵列结构

典型互质阵列主要有简单互质阵列(CPA)、扩展互质阵列(ECA)和展开互质阵列(UCA)[25]3种。

CPA结构如图1所示。

图1 CPA结构

CPA由阵元间距互质的两个ULA交叉构成,分别记为子阵1和子阵2。子阵1有M′个阵元,阵元间距为N′d;子阵2有N′个阵元,阵元间距为M′d。M′和N′为互质整数,d=λ/2,λ为信号波长。

ECA与CPA结构相似,如图2所示。ECA同样由两个稀疏ULA组成,子阵1的阵元数从M′增加到2M′,阵元间距不变,子阵2不变,这样得到一个阵元数为2M′+N′-1的扩展阵列。当阵元数相等时,ECA能够得到比CPA更大的连续虚拟孔径,但ECA较CPA,物理孔径并没有得到扩展,因此ECA与CPA的DOA估计性能相近。

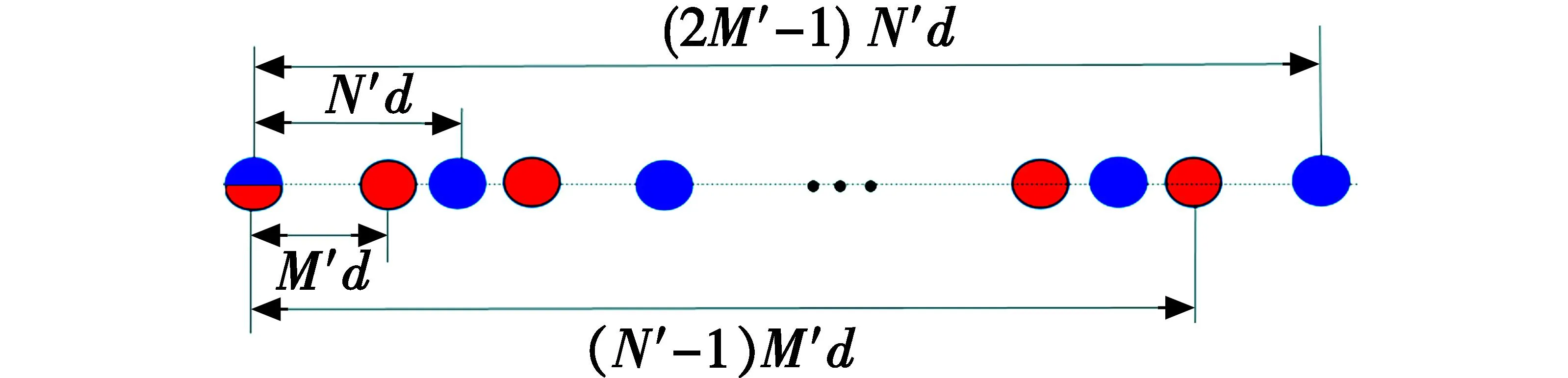
图2 ECA结构

UCA阵列结构如图3所示。

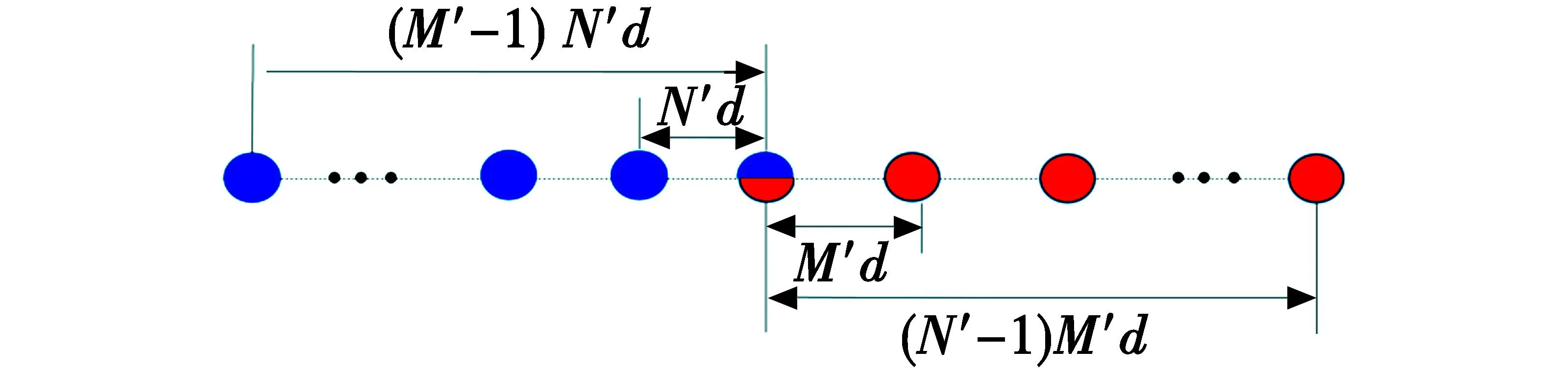
图3 UCA结构

UCA区别于CPA之处则是将CPA的两个子阵沿反方向排列,同样地,子阵1和子阵2阵元数分别为M′和N′,其阵元间距分别为N′d和M′d,子阵1末阵元与子阵2首阵元相重合,UCA继承了CPA的优点,并进一步扩展了阵列物理孔径。不难发现,UCA较CPA和ECA具有更大的阵列孔径,因此其DOA估计性能在三者之中最优异。

1.2 信号模型

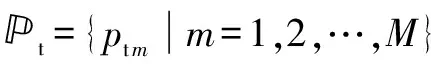
(1)

式中:b(t)=[b1(t),b2(t),…,bM(t)]T,为发射信号;w(t)=[ω1(t),ω2(t),…,ωN(t)]T,为加性高斯白噪声;αt(θk)和αr(θk)分别为第k个目标的发射、接收导向矢量,具体为

αt(θk)=[e(-j2πpt1sin θk)/λ,…,e(-j2πptmsin θk)/λ,…,e(-j2πptMsin θk)/λ]T

(2)

αr(θk)=[e(-j2πpr1sin θk)/λ,…,e(-j2πprnsin θk)/λ,…,e(-j2πprNsin θk)/λ]T

(3)

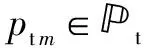
MIMO雷达发射信号是相互正交的,则其协方差矩阵Rb满足

Rb=E[b(t)b(t)H]=IM

(4)

式中:E[·]表示求统计期望运算;(·)H表示矩阵的共轭转置运算;IM表示M×M维的单位矩阵。

对回波信号匹配滤波得

[αt(θ1)⊗αr(θ1),…,αt(θK)⊗αr(θK)]s(t)+

n(t)=(At⊙Ar)s(t)+n(t)

(5)

式中:s(t)=[β1,β2,…,βK]T;n(t)为经匹配滤波后的高斯白噪声;At=[αt(θ1),αt(θ2),…,αt(θK)]和Ar=[αr(θ1),αr(θ2),…,αr(θK)]分别为发射接收阵列方向矩阵; ⊗为Kron积;⊙为Khatri-Rao积。

则回波信号的协方差矩阵为

R=E(x(t)x(t)H)=(At⊙Ar)Rs(At⊙Ar)H+

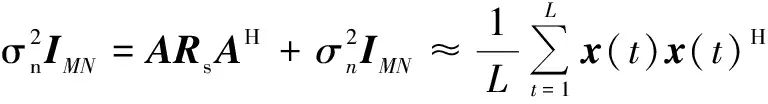
(6)

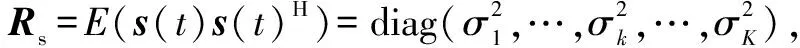
矢量化R得到虚拟域观测向量r,即

(7)

(8)

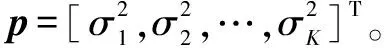
分析式(8)可知,B的虚拟阵元位置可通过物理阵元位置的“和差联合阵列”计算得到[26]。

2 互质阵MIMO雷达DOA估计方法

2.1 基于和联合阵列的DOA估计方法

单基地互质阵MIMO雷达分为简单互质阵MIMO(CPA-MIMO)雷达、扩展互质阵MIMO(ECA-MIMO)雷达及展开互质阵MIMO(UCA-MIMO)雷达。下面以简单互质MIMO雷达为例,分析基于和联合阵列的互质阵MIMO雷达DOA估计方法。假设收发共用同一互质阵,即发射、接收阵列阵元数为Mt=Nr=M+N-1,则总物理阵元数为T=Mt+Nr=2M+2N-2。

(9)

风影明白，当年那个缠着他将竹笛子带来的小姑娘已经消失了，取而代之的已是一个世俗的妇人。说来，红琴的那个世界更有存在的理由，人不能不食五谷杂粮，不能生活在一个没有人间烟火味的梦境之地，世外桃源是不存在的。东泉岭的茶楼再美再好，也不能成为红尘世界的避难所，不能成为另一种寺院。茶楼不开在古色古香的东白湖古镇上，而开在这个荒山野岭，也只有他这个还俗的和尚才能想得出来，或许是他的骨子里依然有着一种看破红尘四大皆空从而遁入空门隐居起来的出世情结。

(10)

由式(5)可知,矩阵At⊙Ar的虚拟阵元位置由物理阵元位置的“和联合阵列”组成,具体为

(11)

选取R中与式(11)中扩展虚拟阵元位置对应的数据,重新排列后得到新的观测矢量为

x0(t)=A0s(t)+n0(t)

(12)

式中:n0(t)为对应位置的噪声向量;A0为

(13)

则新的协方差矩阵为

(14)

然后对式(14)进行特征值分解后利用MUSIC等子空间类算法实现非相干目标DOA估计。

2.2 基于和差联合阵列的DOA估计方法

分析式(8)可知,矩阵B=A*⊙A的虚拟阵元位置由物理阵元位置的“和差联合阵列”组成,“和差联合阵列”可由“和联合阵列”中的元素作差处理得到[26],即

(15)

选取矩阵B中与虚拟阵元对应的阵列流型数据,传统DOA估计算法通常删除同一虚拟阵元位置的多余数据,即冗余删除法,这样会丢失接收信号中的部分信息。为了充分利用所有虚拟阵元数据,文献[26]将多余阵列流型数据进行平均,即冗余平均法,显著提升DOA估计性能。因此,下面简要介绍本文所采用的冗余平均法。

首先,将“和差联合阵列”中同一位置虚拟阵元进行平均,然后,按照虚拟阵元位置有序选取连续数据,构造P×K维的方向矩阵A1。其中,P为和差联合阵列连续虚拟阵元数,由于互质阵MIMO雷达和差联合阵列存在孔洞,可知,P小于2MN+4M+4N-9,P随发射、接收阵元数M和N的值变化。方向矩阵A1为

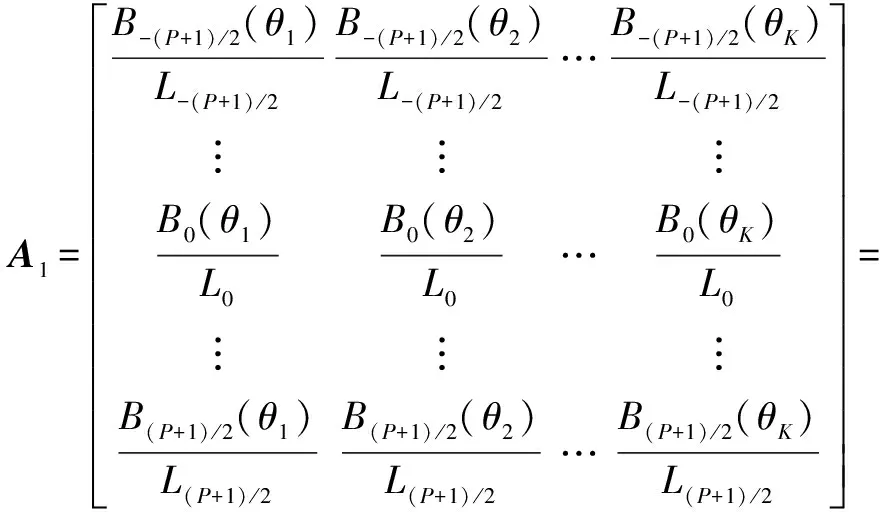
[α(θ1),α(θ2),…,α(θK)]

(16)

式中:Li(-(P+1)/2≤i≤(P+1)/2)为式(15)中第i个虚拟阵元位置的权重;Bi(θk)为B所对应同一虚拟阵元位置的导向矢量之和;α(θk)=[e-jβkz-(P+1)/2,e-jβkz-(P-1)/2,…,0,…,e-jβkz-(P-1)/2,e-jβkz(P+1)/2]T,zi为虚拟阵元位置,-(P+1)/2≤i≤(P+1)/2,βk=2πsinθk/λ。

此时,对应回波信号矢量为

(17)

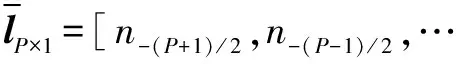
为克服单快拍影响,利用r1构建Toeplitz矩阵

(18)

式中:

(19)

式中:pk为p中的第k个元素;ni为第i个虚拟阵元处的高斯白噪声矢量;zi和zs均为虚拟阵元位置,且-(P+1)/2≤i+s≤(P+1)/2。则式(18)可以表示为

(20)

式中:

(21)

(22)

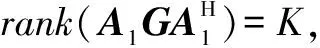
综上所述,总结基于虚拟阵元冗余平均的单基地互质阵MIMO雷达非相干目标DOA估计算法步骤如下:

1) 将回波信号x(t)按照式(5)、式(6)和式(7)依次做匹配滤波、求协方差矩阵和向量化处理得到虚拟域观测向量r;

2) 根据式(16)对矩阵B=A*⊙A中重复的虚拟阵元进行平均处理并选取连续数据,得到方向矩阵A1;

3) 根据式(17)构建新的回波信号矢量r1;

4) 利用r1构建Toeplitz矩阵R1;

5) 对R1进行特征值分解,利用MUSIC算法求得非相干目标DOA。

3 实验仿真

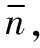
(23)

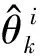
3.1 角度分辨力对比实验(仿真1)

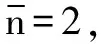
图4 基于和联合阵列、和差联合阵列的MIMO空间频谱对比

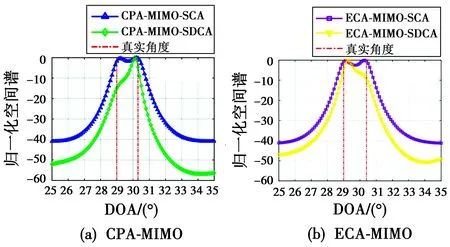
图5 典型互质阵MIMO雷达空间频谱对比

由图4、图5可以发现:1) 图4中,目标入射角间隔2°,分别是29°和31°,基于和联合阵列、和差联合阵列测角的互质阵MIMO雷达均能清晰分辨2个目标,等阵元数的ULA-MIMO雷达空间谱仅1个谱峰,无法分辨2个目标,可见,在同等条件下,互质阵MIMO雷达角度分辨力高于ULA-MIMO雷达;2) 图5中,目标入射角间隔分别为1.3°,1.4°,0.7°,基于和联合阵列测向的互质阵MIMO雷达能够清晰分辨2个目标,基于和差联合阵列测向的空间谱仅1个谱峰,无法分辨2个目标,可见,在同等条件下,基于和联合阵列测向的互质阵MIMO雷达角度分辨力高于和差联合阵列,原因是和差联合阵列在去除冗余及不连续虚拟阵元时将部分信息丢失;3)对比3种典型互质阵MIMO雷达,在同等条件下,UCA-MIMO雷达角度分辨力最高,最小能够区分间隔0.7°的2个目标,CPA-MIMO和ECA-MIMO雷达次之,分别能够区分间隔1.3°和1.4°的2个目标。

3.2 信噪比影响测角精度实验(仿真2)

图6 SNR对测角精度的影响

由图6可以发现:1) SNR与各阵列MIMO雷达基于两种方法的测角精度呈正相关关系;2) 在同等SNR下,互质阵MIMO雷达测角精度比等阵元数的ULA-MIMO雷达更高;3) 在同等SNR下,同一互质阵MIMO雷达采用和联合阵列测角精度比和差联合阵列略高,这是由采用和差联合阵列进行测向时去除冗余及部分不连续虚拟阵元信息造成的;4) 对比3种典型互质阵MIMO雷达,在同等信噪比下,UCA-MIMO雷达测角精度较高,CPA-MIMO和ECA-MIMO雷达次之。

3.3 快拍数影响测角精度实验(仿真3)

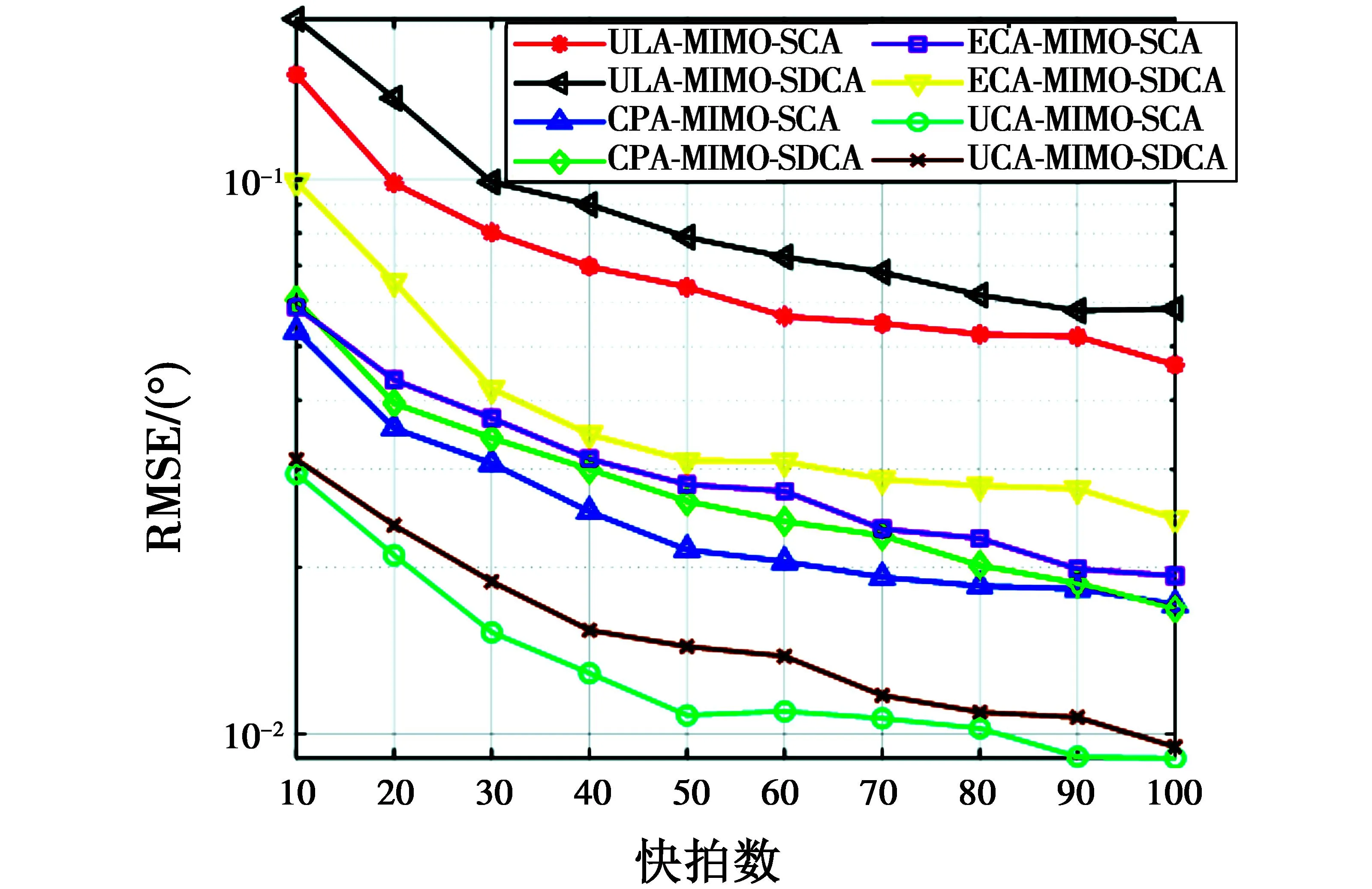
图7 快拍数对测角精度的影响

由图7可发现:1) 快拍数与各阵列MIMO雷达基于两种方法的测角精度呈正相关关系;2) 在同等快拍数下,互质阵MIMO雷达测角精度比等阵元数的ULA-MIMO雷达更高;3) 在同等快拍数下,同一互质阵MIMO雷达采用和联合阵列测角精度比和差联合阵列精度略高,这是由采用和差联合阵列进行测向时去除冗余及部分不连续虚拟阵元信息造成的;4) 对比3种典型互质阵MIMO雷达,在同等快拍数下,UCA-MIMO雷达测角精度较高,CPA-MIMO和ECA-MIMO雷达次之。

3.4 自由度对比实验(仿真4)

实验条件:SNR为0 dB,快拍数L=100,均匀设置目标入射角度间隔,各阵列MIMO雷达基于两种方法测向时均采用MUSIC算法,测得的空间谱见图8,图8(a)～8(d)和图8(e)～8(h)为各阵列MIMO雷达分别基于和联合阵列、和差联合阵列测向的空间谱图,正确测量信源的个数就是该阵列MIMO雷达的自由度。

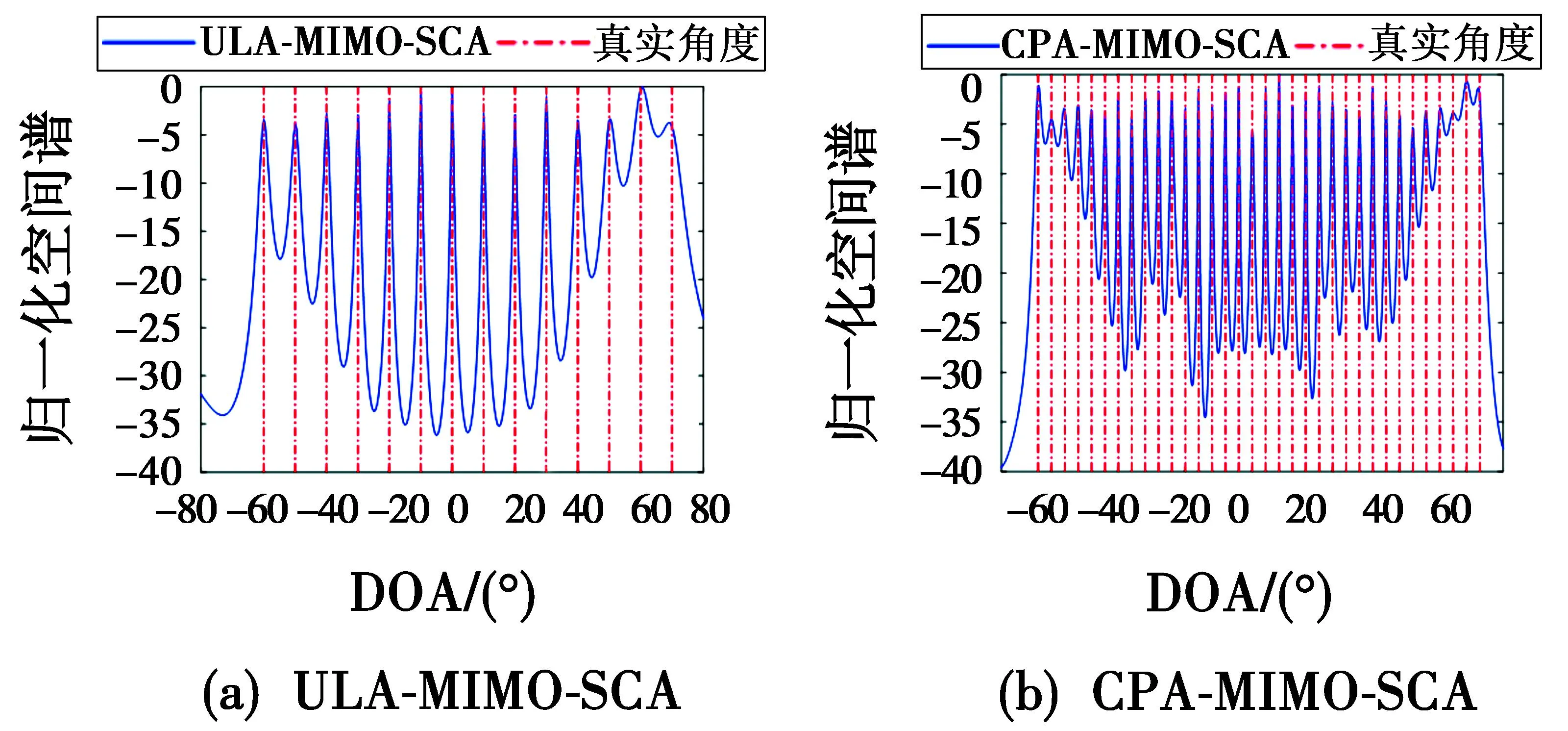
图8 DOA估计空间频谱图

由图8可以发现:1) 在同等条件下,基于两种方法测角的互质阵MIMO雷达自由度均高于均匀线阵MIMO雷达;2) 在同等条件下,基于和联合阵列测角的各互质阵MIMO雷达自由度均高于和差联合阵列,原因是和差联合阵列将冗余和不连续虚拟阵元信息丢失;3) 对比3种典型互质阵MIMO雷达,在同等条件下,UCA-MIMO雷达自由度最高,CPA-MIMO和ECA-MIMO雷达次之。

4 结束语

本文以非相干信源为对象,结合MUSIC算法,综合分析了单基地互质阵MIMO雷达基于和联合阵列与和差联合阵列的DOA估计性能。互质阵MIMO雷达较均匀线阵MIMO雷达具有更高的角度分辨力、测角精度和自由度,这是因为物理阵元数目一定的前提下互质阵较均匀线阵具有更大的阵列孔径,叠加MIMO雷达的虚拟孔径扩展能力具有更好的角度分辨力和测角精度。对于互质阵MIMO雷达,基于和联合阵列DOA估计方法的角度分辨力、测角精度及自由度最高,基于和差联合阵列DOA估计方法的性能稍差,主要原因是基于和差联合阵列的DOA估计方法将冗余及不连续虚拟阵元信息丢失。对比3种典型互质阵MIMO雷达,在同等条件下,展开互质阵MIMO雷达角度分辨力、测角精度和自由度最高,简单互质阵MIMO雷达和扩展互质阵MIMO雷达次之。