基于PRT与频率联合调制的随机跳频雷达成像方法

胡杰民, 滕俊鹏, 邹 博, 杨 旭

(1.浙江理工大学信息学院,杭州 310000; 2.陆军航空兵研究所,北京 101000)

0 引言

雷达抗欺骗干扰是雷达探测与识别中的核心关键技术。干扰的产生依赖于电子支援措施(ESM)截获探测雷达发射信号,并通过数字射频存储器(DRFM)存储、调制、转发等步骤将满足信号相参性的干扰发射回雷达信号来波方向[1]。因此,雷达波形抗干扰可从两个方面进行考虑:一是降低信号截获概率[2],使侦察设备无法感知雷达信号;二是破坏干扰信号的相参性,从而降低干扰信号的相参累积增益,使之无法形成有效干扰。雷达信号的波形设计与相参处理是雷达系统设计中的一个研究重点[3],在很大程度上决定了雷达的探测和抗干扰能力,因此,设计合适的信号波形对于提高雷达系统的探测精度和对抗干扰至关重要。

在低截获波形设计中,步进频信号体制应用最为广泛[4],它将探测信号的能量分散于多个调制频率线性跳变的单频子脉冲,并通过相参处理获得高信噪比的距离像[5]。然而,频率的线性跳变使简单的延时转发就能够形成有效干扰,给后端信号处理带来了巨大挑战。具备抗干扰性能的信号体制主要包括随机捷变频体制[6]、随机噪声体制[7]、随机跳频体制[8]等。传统捷变频雷达,没有考虑脉间相参合成高分辨距离像,难以提取目标细节信息。随机噪声体制的信号频率由噪声连续调制,噪声的全频带特性导致信号难以抽样存储和恢复,只能通过延迟相关等手段处理,难以实际应用[9]。随机跳频信号可看作是噪声信号的离散形式[10],它通过发射一组频率随机跳变的单频子脉冲实现对目标区域的探测。相比噪声信号大带宽导致的存储困难,单频信号可直接采用数字频率无损存储并合成,随机跳频信号是一种低截获且抗干扰性能优良的信号波形[11]。文献[12-13]对随机跳频雷达的低副瓣波形进行了研究。

利用随机跳频雷达对目标进行成像时,目标运动引入的相位高次项将导致距离像散焦,需要进行运动补偿[14]。文献[15]利用相邻距离像的互相关结果对目标速度进行估计,其补偿精度与距离分辨率相当,无法达到随机跳频信号波长量级的补偿精度要求;文献[16]在距离波门内搜索代价函数极值确定目标速度,算法性能敏感于搜索的步长和范围;文献[17-18]将压缩感知理论应用于随机跳频雷达成像,在构造原子字典时需要遍历目标所有可能的速度和加速度,巨大的计算量难以满足实时应用条件;文献[19]提出基于互补码调制的速度估计方法,通过发射具有互补关系的相邻脉冲串实现速度的高精度估计,其缺点是需要两个脉冲串才能完成速度估计,降低了雷达数据率。

采用运动补偿[20]的思路实现随机变频雷达高分辨成像时,通常以牺牲计算量或估计精度作为代价。本文从波形设计角度出发,通过脉冲重复时间(Pulse Repe-tition Time,PRT)与频率联合调制消除目标运动引入的相位高次项,并设计了基于核函数的快速成像算法,在目标运动参数未知的情况下,实现了运动目标的高质量成像。利用仿真数据和实测数据的实验结果验证方法的有效性。该方法兼顾了雷达信号的抗干扰性能与信号处理的时效性,为弹载雷达探测提供一种可行思路。

1 常规随机跳频雷达信号回波建模

图1所示为常规随机跳频雷达波形。如图1所示,随机跳频雷达通过处理一组频率随机排列的相参脉冲串获得高分辨距离像。每组脉冲串包含N个单频子脉冲,脉冲宽度为T,脉冲重复周期为Tr。假设随机跳频雷达带宽为B,最小跳频步长为Δf,则子脉冲数满足NΔf=B。随机跳频雷达信号可表示为

(1)

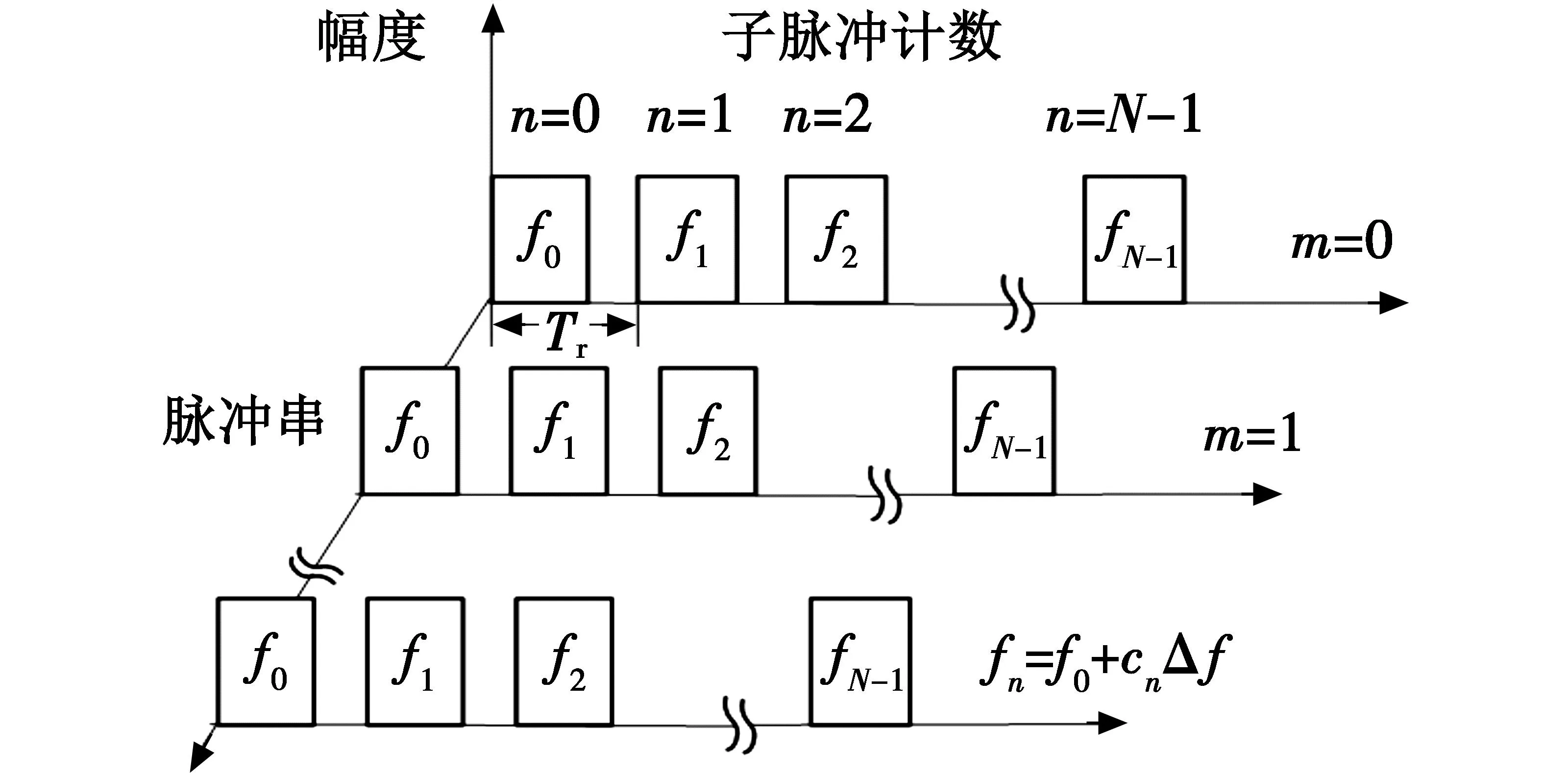
图1 常规随机跳频雷达波形示意图

式中:f0为信号载频;cn为跳频系数,表示将n=0,1,…,N-1这N个整数随机排列后,第n个数的值,对应的第n个子脉冲频率为fn=f0+cnΔf;rect(·)表示单位矩形函数,表达式为

(2)

假设目标包含K个散射中心,第k个散射中心的强度为σk,第n个子脉冲发射时刻第k个散射中心与雷达的距离为rk(n),则rk(n)随着发射时间的变化可表示为

rk(n)=rk0+vlosnTr

(3)

式中:rk0表示初始时刻第k个散射中心与雷达的距离;vlos为目标速度在雷达视线方向的投影分量。

目标回波混频后可表示为

(4)

式(4)相位项中:第1项为常数项,对成像没有影响;第2项为各散射中心距离引入的随机非线性相位延迟,是高分辨成像所需信息;第3项为目标运动引入的附加相位项,既包括运动引入的线性相位项,也包括频率随机调制与目标运动的高次耦合项,将造成距离像的散焦。在合成高分辨距离像时,现有方法通常对vlos进行估计,然后构造补偿因子,消除运动附加项的影响,vlos的估计需要大量计算资源且存在估计误差。

2 PRT与频率联合调制的随机跳频雷达成像方法

2.1 回波建模

PRT与频率联合调制的随机跳频信号如图2所示。

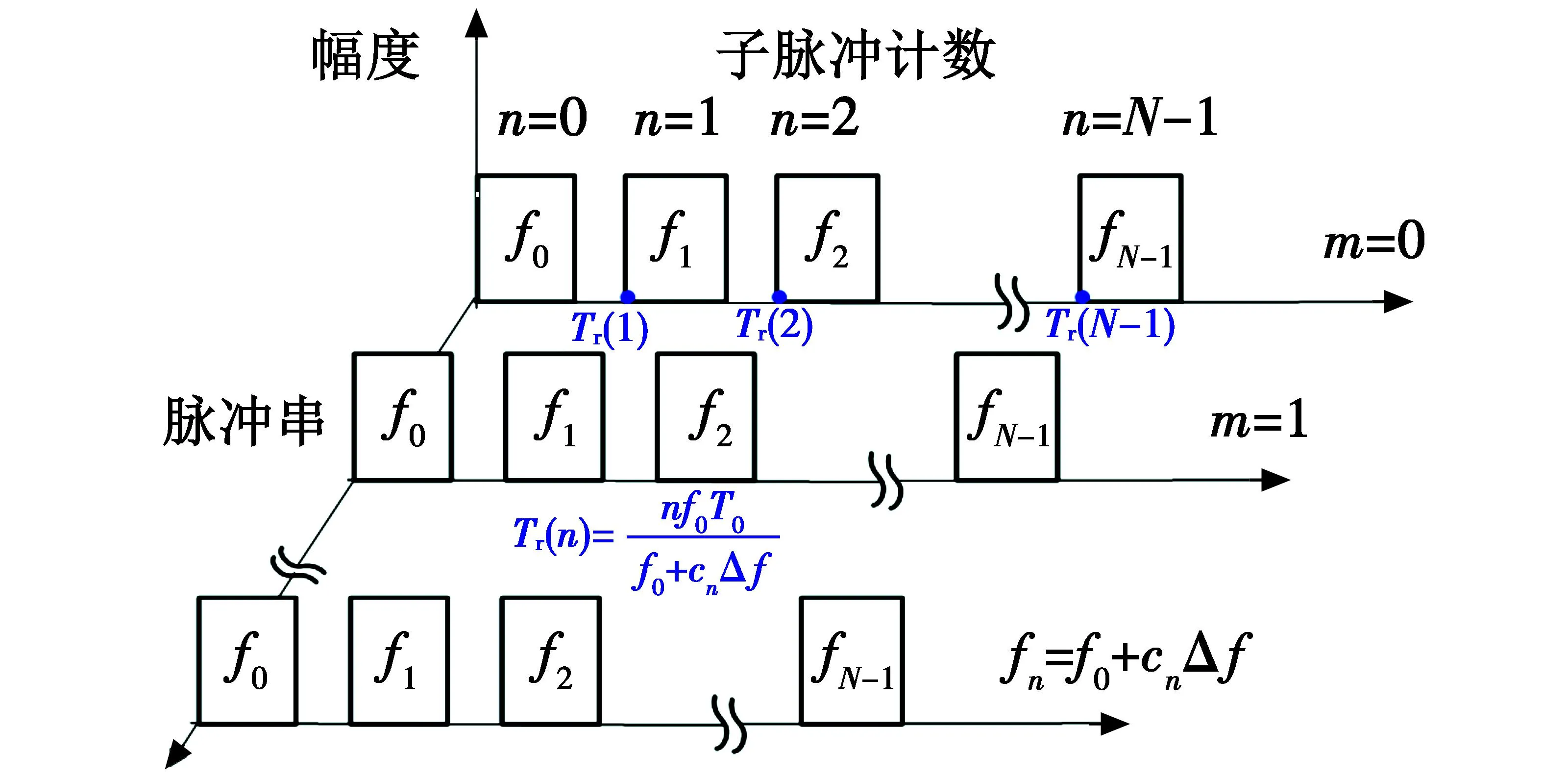
图2 PRT与频率联合调制的随机跳频雷达波形示意图

每组脉冲串除PRT外,其他信号参数与传统随机跳频信号一致。第n个子脉冲重复时间为

Tr(n)=(nf0T0)/(f0+cnΔf)

(5)

式中,T0为脉冲重复时间参数,大小与常规随机跳频信号的脉冲重复时间一致。将式(5)代入式(3),可得

(6)

因此,目标回波混频后可表示为

(7)

通过对比式(4)可知,频率非线性调制与目标运动耦合的相位高次项已经消除,然而,回波相位由散射中心距离引入的随机非线性相位与速度引入的线性相位组成。线性相位与非线性相位的叠加导致FFT或核函数方法均无法直接高分辨成像。

2.2 成像方法

由上述分析可知,尽管PRT与频率联合调制消除了运动引入的相位高次项,散射中心距离调制的非线性相位和运动调制的线性相位仍然叠加于回波之中,难以直接进行高分辨成像。本文采用核函数补偿与FFT相结合的方法实现高分辨距离成像,分别针对每个距离单元利用核函数补偿随机非线性相位项,得到对应该距离单元的线性相位回波,然后利用FFT实现线性相位信号的聚焦。具体过程如下所述。

假设随机跳频的信号的距离分辨率为Δr,成像距离门内包含的距离单元数为L,分别针对每个子脉冲的第l个距离单元设置对应的核函数表示为

(8)

式中,n为子脉冲计数。利用各子脉冲回波sr(n)分别计算每个距离单元补偿后的基带回波,补偿过程为

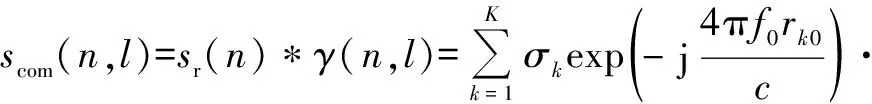
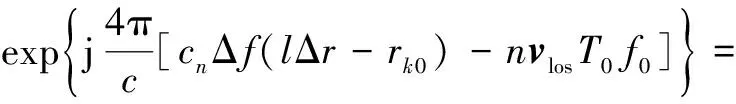
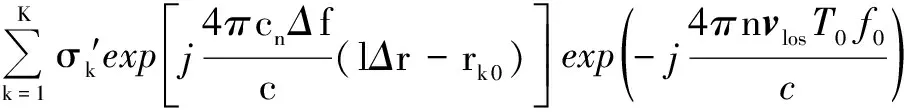
(9)

(10)

可见,补偿后第k1个散射中心回波表现为n的相位线性变换序列,经过FFT后,回波能量将相参积累于第m=2NvlosT0f0/c个多普勒单元;同时,其他散射中心分量的非线性相位调制依然存在,FFT后处于散焦状态。因此,分别对每个距离单元的回波序列进行FFT变换,即可在第m=2NvlosT0f0/c个多普勒单元获得该距离单元的相参积累结果。

对l个距离单元做FFT变换,即

(11)

实际应用中目标速度未知,在一个脉冲串成像时间内,假定目标速度近似不变,则目标上所有散射中心的能量均搬移至第m=2NvlosT0f0/c个多普勒通道中,因此将能量最大的多普勒通道中的距离像作为目标高分辨距离像进行输出。成像流程说明如图3所示。

图3 改进随机跳频波形成像流程

3 性能分析

3.1 时间调控精度分析

图4所示为本文脉冲重复时刻与常规随机跳频信号脉冲重复时刻的比较情况。

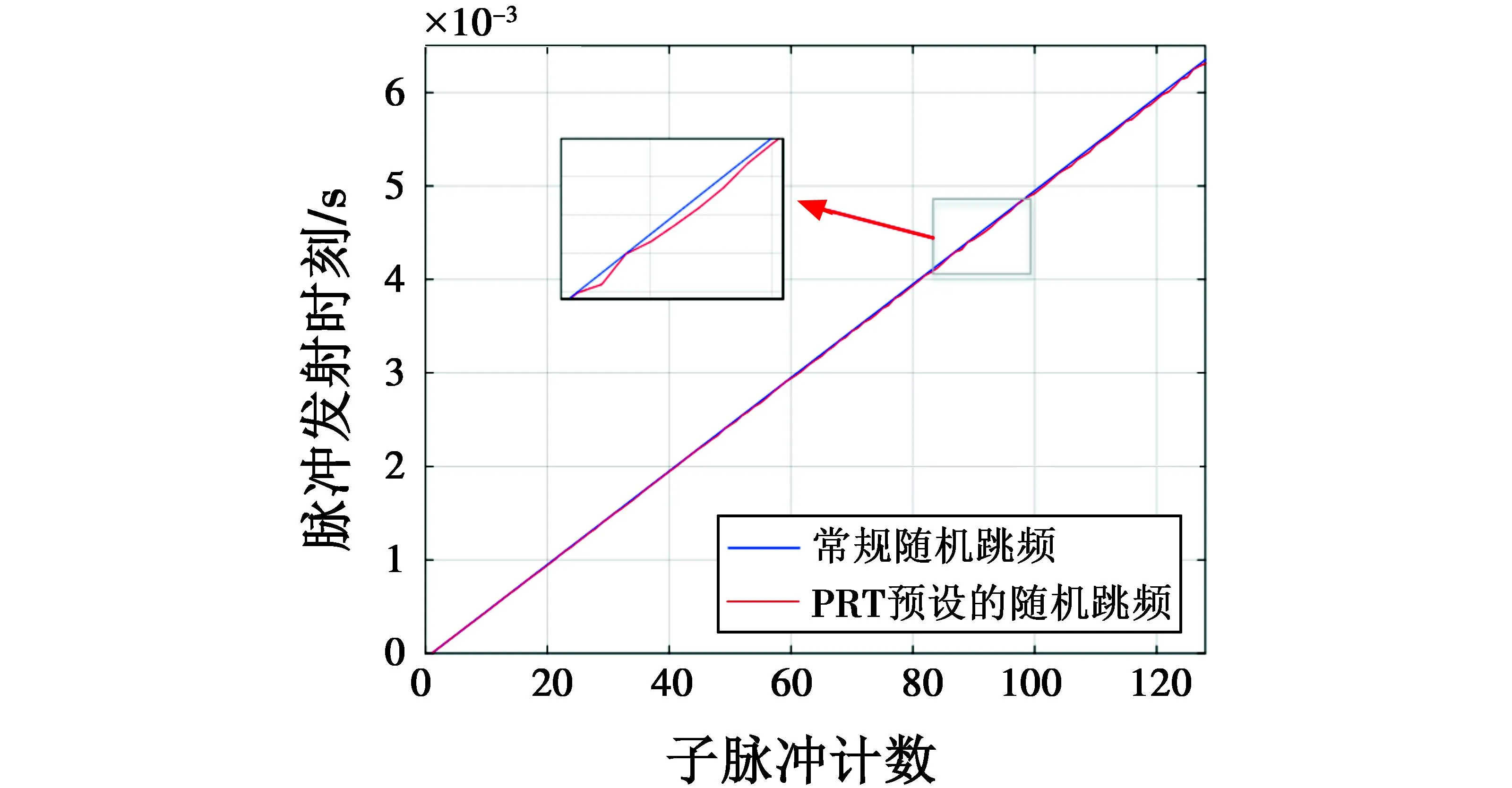
图4 改进随机跳频波形与常规随机跳频波形的脉冲发射时刻比较

由式(5)可知,所设计PRT由子脉冲调制频率精确决定。而实际应用中,雷达系统通常基于晶振参考源工作频率对PRT进行调控,调控精度存在约束。假定雷达硬件对脉冲重复时刻的调控误差最大为Δt,调控误差将影响脉冲发射时刻目标的距离。式(6)修正为

rk(n)=rk0+vlos[Tr(n)+Δt]

(12)

代入式(7)可得

(13)

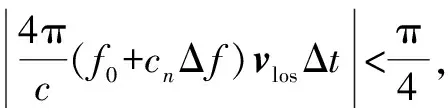
(14)

假定目标的最大速度为vmax,则式(14)可简化为

(15)

当雷达载频为f0=35 GHz,B=256 MHz,vmax=10 m/s时,需满足Δt<53.182 μs。假设目标包含4个散射中心,相对距离表示为0 m,4.5 m,7.8 m,11 m,散射强度分别为1,1,1,1,图5所示为雷达系统时间调控误差Δt分别为10 μs,20 μs,50 μs,100 μs时的高分辨距离成像结果,幅度无单位。

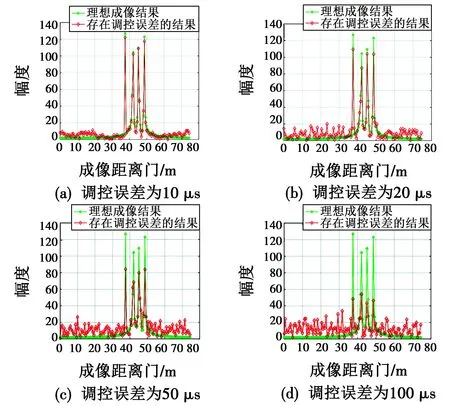
图5 不同调控误差下的成像结果

由图5可见,当调控误差小于50 μs时,高分辨距离像能够有效聚焦,而当调控误差达到100 μs时,时间调控误差引入的附加相位项将导致高分辨距离像的散焦,这与式(15)的分析结果一致。需要指出,实际应用中,雷达系统时间控制精度能达到0.1 μs甚至更高。因此,现有系统时间调控精度能够满足本文波形设计需求。

3.2 距离遮挡

与常规随机跳频信号相比,新波形的PRT是不断变化的,会造成子脉冲的最大探测距离随时间改变;若目标回波时延大于当前脉冲重复周期,雷达接收机无法对回波进行采样,将会造成距离遮挡现象,因此需要对新波形的探测距离进行分析,如图6所示。

图6 距离遮挡分析

假设Δf=2 MHz,子脉冲数为N=128,T0=50 μs,随机产生一组新波形的PRT(图6(a)),可见,与常规随机跳频信号体制相比,不同子脉冲的PRT不断变化,因此,随着探测距离的增加,子脉冲被遮挡的数目逐渐增加。随机产生10000组随机跳频信号波形,然后计算不同探测距离对应的平均子脉冲遮挡数,得到如图6(b)所示结果。可见:当探测距离为4.5 km时,被遮挡的子脉冲数占比为5%;探测距离6.5 km时,被遮挡的子脉冲数占比为21%;当探测距离为7 km时,被遮挡的子脉冲数占比约为31%,而常规随机跳频信号在探测距离7.5 km以内,不存在距离遮挡现象。因此需要对新波形的探测距离进行进一步分析。

假设目标包含4个散射中心,相对距离表示为0 m,4.5 m,7.8 m,11 m,对应散射强度表示为1,1,1,1,目标处于静止状态,雷达信号参数同前文。图7所示为目标探测距离分别为4.5 km,6 km,7 km时新波形的子脉冲遮挡情况,以及采用新波形的高分辨距离成像结果,为了方便比较,图7中还给出了常规随机跳频波形的高分辨成像结果,幅度无单位。

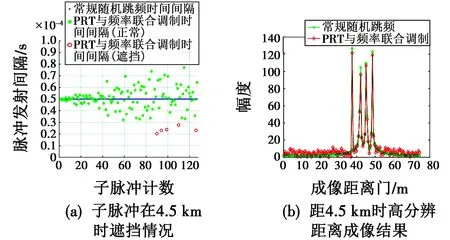
图7 距离遮挡及成像结果比较

由图7可见,当探测距离为4.5 km时,被遮挡的子脉冲数为6,对新波形进行高分辨距离成像时,目标散射中心均能有效聚焦,同时,由于6个子脉冲回波缺失的影响,导致新波形的距离像幅度较传统随机跳频信号略有下降;当探测距离增加到6 km时,被遮挡的子脉冲数增加至23,此时高分辨距离像幅度下降约25%;当探测距离增加至7.5 km时,被遮挡的子脉冲数增加至64,此时高分辨距离像的幅度明显下降,导致目标检测困难。因此,新波形的有效探测范围为6 km,为传统随机跳频信号有效探测距离的80%。

3.3 计算量分析

新波形高分辨距离成像流程如图3所示,成像计算量主要由基于核函数相关和FFT变换组成,高分辨距离单元数通常与采样频点数N一致。每个频点采用核函数补偿需要N次复数乘法,N个频点采用核函数补偿的总计算量为ηa=N2次复数乘法。此外,FFT变换需要对每个距离单元执行一次,每次需要的计算量为NlbN/2次复数乘法和NlbN复数加法。因此FFT变换步骤的总计算量为N2(lbN)/2次复数乘法和N2lbN复数加法。

常规设计的随机跳频在已知计算量的基础上再对相位高次耦合项中vlos进行补偿估算,以最小波形熵速度估计方法[19]为例,对计算复杂度进行比较。假设需要搜索的速度采样点数为P,对于每个速度采样点,需要2N次复数乘法补偿所有频点回波,然后采用核函数方法进行成像,每次成像需要N2次复数乘法和N(N-1)次复数加法,然后计算距离像的熵值,每次计算需要计算量为N次复数乘法和(N-1)次复数加法,因此总的计算量为P(2N+N2)N次复数乘法和PN(N-1)2次复数加法。两种方法的计算量总结如表1所示。

表1 不同方法成像计算量比较

由表1可见,采用新波形探测时,避免了速度估计引入的计算量,因此具有很高的计算效率。

4 实验验证

4.1 仿真数据成像验证

假设子脉冲数为128,带宽为256 MHz,由此得到最小跳频步长Δf=2 MHz,雷达载频为35 GHz,脉冲重复时间参数T0=50 μs。目标包含4个散射中心,相对距离表示为0 m,4.5 m,7.8 m,11 m,对应散射强度值表示为1,1,1,1。

目标距离雷达为3 km,此时距离遮挡现象可忽略。当目标速度分别为0 m/s,5 m/s,10 m/s,15 m/s时,分别采用新波形和传统随机跳频波形进行高分辨距离成像,得到的结果如图8所示,幅度无单位。

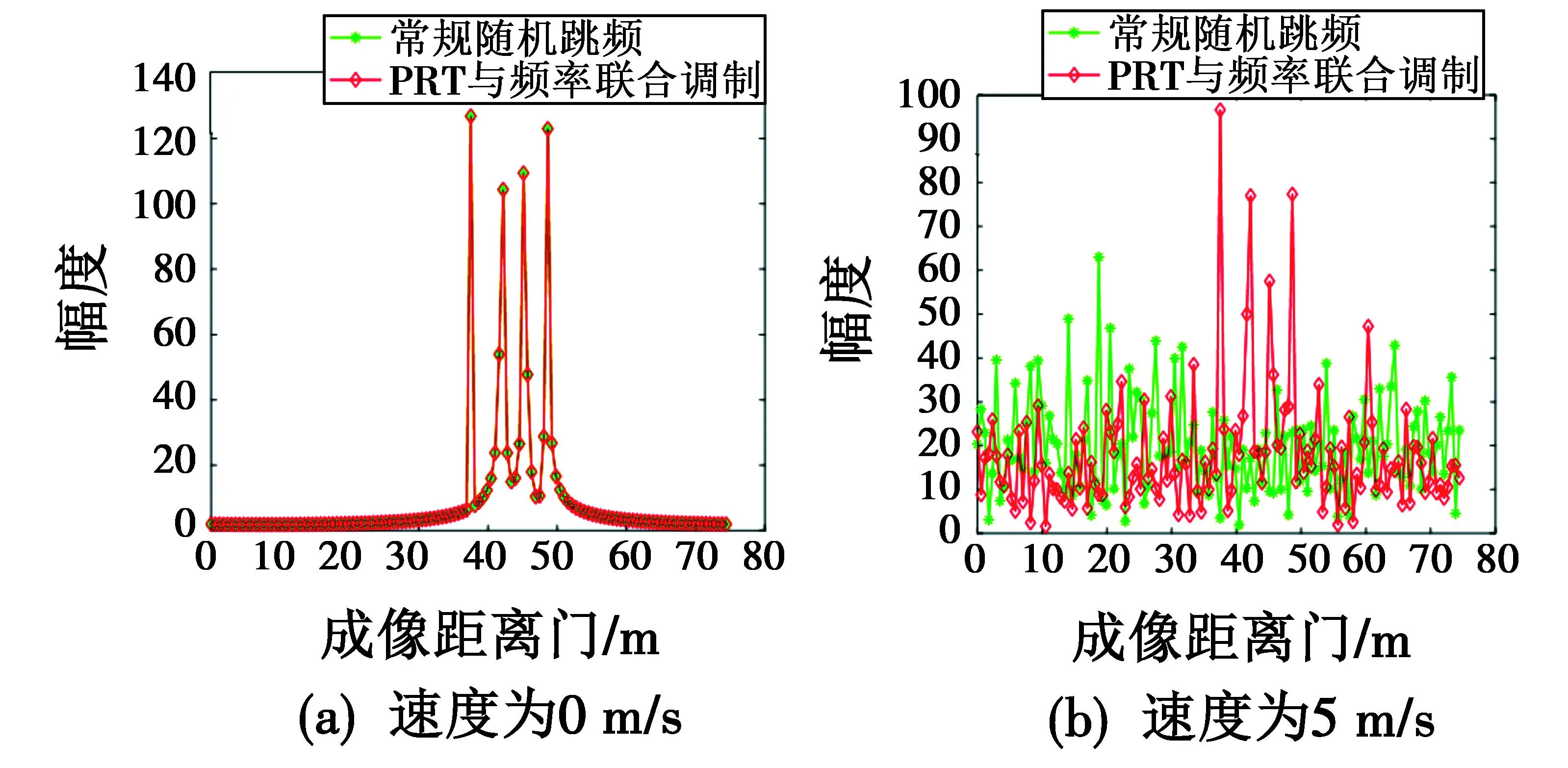
图8 高分辨距离成像结果比较

由图8可见,当采用传统随机跳频波形时,高分辨距离像对速度非常敏感,目标运动时距离像散焦严重,而采用本文设计的波形时,目标速度引入的相位高次项被消除,因此距离像聚焦性能良好,仿真结果验证了本文设计波形的有效性。

4.2 实测数据成像验证

理想的散射点模型在目标处于光学区时适用,然而它并不能完全反映复杂目标的电磁散射机理,本文利用实测数据验证本文方法的有效性。由于目前没有本文所设计雷达信号的实测数据,因此需要对实测数据进行转换,其过程如下:首先对实测线性调频信号解线频调,获得目标距离像序列,然后通过逆傅里叶变换重新变换到原始数据域后,根据跳频系数cn重新排列得到随机跳频信号的回波数据。假设目标运动速度为v,时间参数T0=50 μs,雷达载频为35 GHz,带宽为300 MHz,一帧脉冲串包含256个子脉冲,每个子脉冲回波相位延迟项可由式(6)计算得到。对每一个子脉冲频点数据分别乘以相对应的相位延迟项即可转换为所设计波形的回波数据。

假设常规随机跳频信号的脉冲周期为T0,图9所示为目标速度分别为5 m/s,10 m/s,15 m/s情况下利用常规随机跳频信号和所提信号的距离像成像结果,幅度无单位。

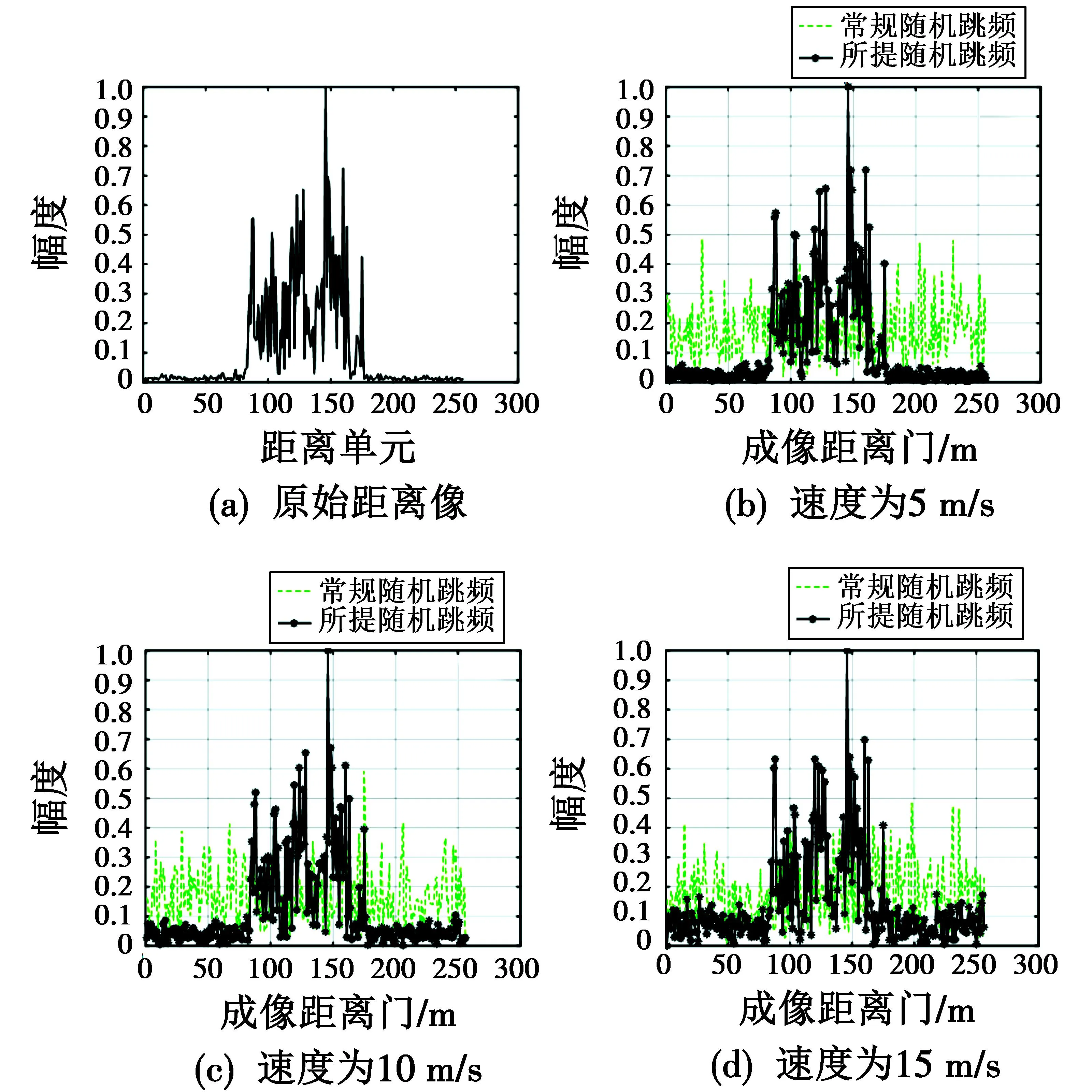
图9 实测数据成像结果比较

由图9可知,目标运动导致随机跳频信号合成的距离像散焦严重,不能反映目标散射点的径向分布,而所提信号没有高次项的干扰,距离像没有产生散焦现象。实测数据的成像结果进一步验证了本文方法的有效性。需要指出的是,所提方法对于坦克、舰船等传统地/海面目标均适用,但对于速度更高的空中目标,需要考虑目标高速运动引入的速度模糊,这与脉冲多普勒雷达类似。

5 结束语

传统随机跳频信号高分辨距离成像时,运动与频率耦合引入的相位高次项将导致距离像散焦。本文从波形设计的角度出发,在推导回波相位表达式的基础上,提出一种新的随机跳频波形,该波形是通过PRT与频率联合调制消除目标运动引入的相位高次项,然后采用核函数与FFT相结合的方式实现高分辨距离成像。通过仿真实验与传统随机跳频信号的探测效果进行对比,结果表明,新波形在探测距离略有降低的情况下,有效消除了目标速度的散焦效应。新波形兼顾了雷达信号的抗干扰性能与信号处理的实时性,为弹载雷达探测提供了一种可行思路。