基于多尺度Harris角点检测的图像配准算法

尚明姝, 王克朝,2

(1.哈尔滨学院信息工程学院,哈尔滨 150000; 2.哈尔滨工业大学计算机科学与技术学院,哈尔滨 150000)

0 引言

图像配准是为同一场景的数幅有重叠的小图像,计算各幅图像间的变换模型,确定几何对应关系,使重叠部分对齐,进而合成一幅大场景图像的技术,在医学图像处理、人工智能、卫星图像分析、军事目标识别等领域都有重要应用。

1988年,HARRIS等[1]提出的Harris算法是一种经典的特征点检测算法,该算法提取的特征点数量适中、计算量小、对图像旋转、变换视角都有较强的鲁棒性,抗噪能力佳,但由于是在单一尺度下检测特征点,特征点不具有尺度不变性,不适用于图像尺度变化较大的场合;2004年,LOWE[2]提出的SIFT算法虽具备尺度不变性,但检测得到的特征点数量过多、计算量大、运算时间较长、占用系统资源过多。而将尺度空间和Harris算法相结合使用,既可使特征点具备尺度不变性,又能提高算法效率,是进行相关研究的一个方向。

MIKOLAJCZYK等[3]提出的Harris-Laplace算法,为图像建立多尺度空间,令Harris算子在多尺度空间内检测特征点,特征点便具备了尺度不变性。但由于没有进一步的特征点提纯运算,算法整体精确度不高;徐贤峰等[4]提出对多尺度Harris特征点分组来解决算法精准性问题,但效果一般;年华等[5]提出将多尺度Harris算子和SURF描述符相结合使用,但SURF描述符为较复杂的64维向量,算法整体效率不高。

针对以上问题,本文提出一种高效、简便的算法。首先,利用高斯核函数为图像建立多尺度空间,使用 Harris算子在多尺度空间提取特征点,这样特征点便具备了尺度不变性,简化128维的SIFT特征描述符,建立简单的32维特征向量,采用特征点的最近邻与次近邻的欧氏距离比值来衡量特征点的相似性完成特征匹配;然后,使用改进的相似三角形法筛选匹配点,再利用改进的K-means算法对特征点分组,使相同区域的特征点聚在一起,不同区域的特征点彼此远离;最后,将特征点分为不同的组,令改进的RANSAC算法从不同组中选取特征点计算变换矩阵,可避免选取的特征点距离过近,算法陷入局部最优。实验验证了本文算法的运算量较小、精确度较高。

1 特征点提取与描述

1.1 特征点提取

Harris算子通过计算每个点的自相关矩阵得到该点的Harris响应值,若响应值大于阈值,则该点为特征点。但该算法简单、计算量小,检测出的特征点具有旋转和平移不变性,不具有尺度不变性,特征点定位精确度不高,因此提出一种改进多尺度Harris特征点检测算法。

1) 生成多尺度空间。

令一系列不同尺度的高斯核函数与原始图像做卷积运算生成多尺度空间[6]。

图像尺度变换

Iout(x,y,σ)=G(x,y,σ)⊗Iin(x,y)

(1)

(2)

其中:σ为当前积分尺度;Iin(x,y)为原始图像;Iout(x,y,σ)为变换后的图像;G(x,y,σ)为高斯核函数。

2) 特征点检测。

多尺度Harris自相关矩阵定义为

(3)

式中:σD为微分尺度;Ix(x,y,σD),Iy(x,y,σD)分别为图像经过高斯平滑后在x,y方向的偏导数。

多尺度Harris算子定义为

(4)

3) 求Harris最大值点。

在各尺度空间,以Harris角点为中心的8邻域内,求Harris响应值最大的点,该点作为候选特征点。

4) 利用LoG函数筛选特征点。

计算候选特征点的LoG值,若其LoG值在当前尺度和上下相邻尺度的8邻域内均为极大值点则该点为最终特征点,即

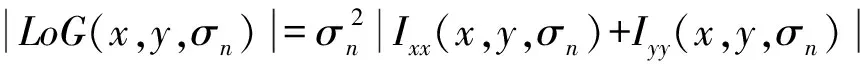
(5)

式中:σn为当前尺度;Ixx,Iyy分别为I(x,y,σn)在x,y方向的二阶偏导数。

1.2. 特征点描述

1.2.1 特征点主方向

为使特征点具有旋转不变性,还需为其指定主方向[7]。以特征点为圆心,1.5σ为半径(σ为特征点的尺度因子),形成一圆形邻域,计算圆形邻域内每个像素的梯度模值和方向,即

(6)

(7)

利用直方图统计各像素的梯度方向,梯度直方图一柱代表10°,共有36柱,直方图峰值即为特征点的主方向。式中,L为特征点所处的尺度空间。

表1 实验数据

1.2.2 特征向量

将以特征点为圆心、8为半径的圆形邻域划分成2×2个子窗口,每个子窗口是一个4×4子区域。在每个子窗口内计算各区域的像素梯度值与方向,再以45°为间隔,累计8个方向的梯度值,形成一个种子点。一个特征点有4个种子点,每个种子点又有8个方向向量,这样构成了特征点的32个方向向量即32维特征向量,为减少光照变换的影响,对特征向量做归一化处理。32维特征向量如图1所示。

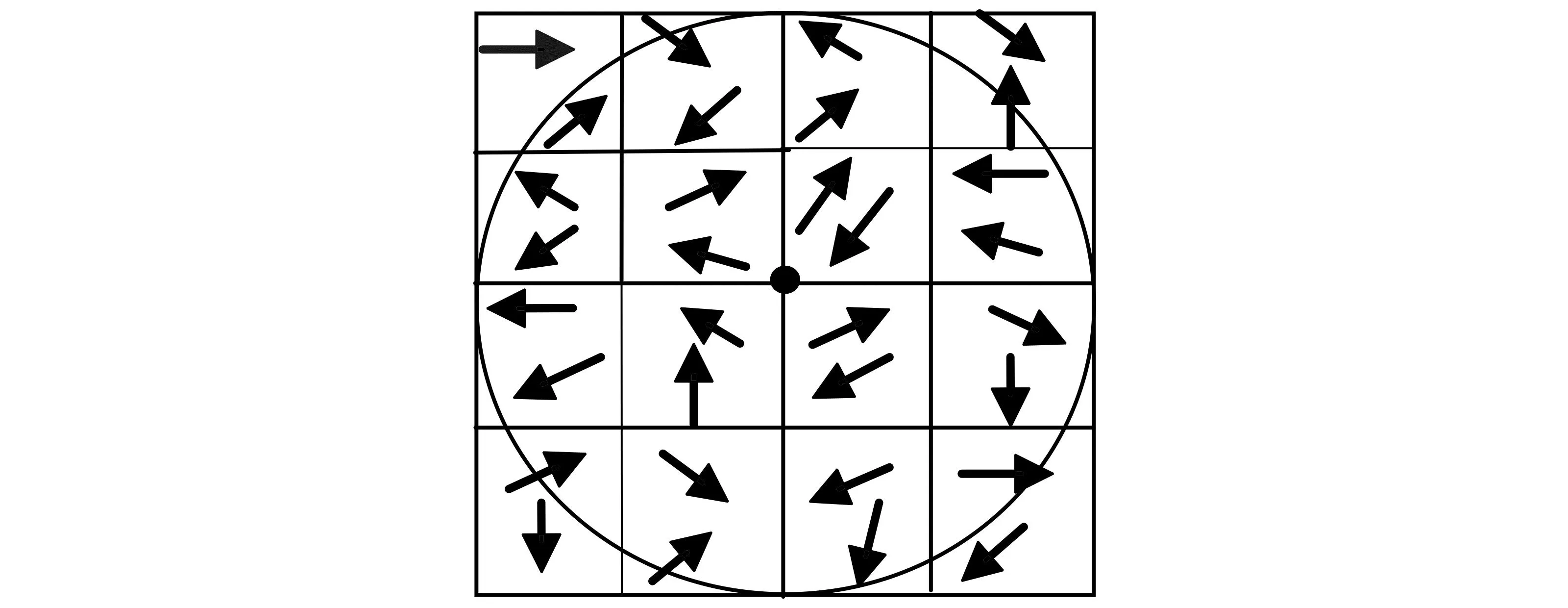
图1 32维特征向量

1.3 特征点匹配

本文利用最近邻法[8]匹配特征点,即若特征点的最近邻与次近邻的欧氏距离比值小于阈值,则该特征点与其最近邻点为匹配特征点。

2 改进相似三角形法筛选匹配点

在待配准2幅图像中取任意3对匹配点,在2幅图像中分别形成1个三角形,组成1个三角形对。三角形具有平移、缩放、旋转不变性,可以适应图像平移、尺度变化、旋转变化的情况,根据三角形对的关系,利用三角形上匹配点的对应位置,可筛选匹配点。正确的匹配点相对位置满足一定的变换关系,若2幅图像中1个三角形对满足三角形的边长比例差和对边夹角差均近似相等(在阈值范围内),则这2个三角形为相似三角形,相似三角形对所对应的2幅图像中的匹配点为正确匹配点。

张东兴等[9]提出在待配准2幅图像中任取3对匹配点组成2个三角形,若它们是相似三角形,则取其中2点为基准点,与图中任一剩余匹配点组成三角形对,判断其相似性。因为基准点是任意选择的,后面所有三角形的相似性验证都包含基准点,若基准点选择不当,则导致错误匹配点数量激增,算法失败。本文提出一种改进算法,不设固定基准点,任取2幅图像的1对匹配点,在以其为中心的圆形邻域内任选2对匹配点,与中心点组成三角形,判断这2个三角形的相似性,相似三角形对应的匹配点为正确匹配点。重复以上过程直至所有特征点均被选择过。

相似三角形判定条件为

(8)

(9)

其中:l为对边比例差阈值;θ为角度差阈值。则满足式(8)、式(9)的三角形对为相似三角形对。

算法步骤:

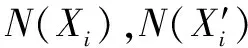
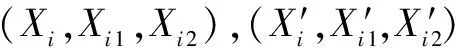
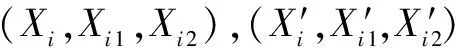
6) 返回步骤1),直至图像I1,I2中所有未选择过的匹配点均被选中。

3 图像变换模型

2幅图像间的平移、旋转和变形,可用仿射变换[10]描述,即

(10)

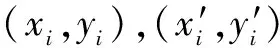
(11)

4对匹配点可得8个方程即可求解变换矩阵H,把I1,I2对应起来。

4 计算变换模型

4.1 利用改进K-means算法对特征点分组

RANSAC算法[11-12]随机选取4对匹配点,若选取的匹配点距离过近,则变换矩阵偏差会较大,无法正确匹配图像。利用K-means算法[13-14]为特征点分组,同一片特征点分为一组,各组之间相隔较远,再从各组中随机抽取匹配点进行RANSAC运算,计算变换矩阵,以免算法陷入局部最优。

经典的K-means算法随机选择类初始中心点,相邻近的点也有可能成为不同类的初始中心点,而分类结果不确定,可能会导致特征点分组失败。本文根据特征点的约束关系,计算特征点的紧密度,从而选出高质量的类初始中心点,优化算法性能,特征点可得更好的分组。

4.1.1 选择类初始中心点

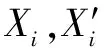
(12)

式(12)为以特征点Xi为中心的圆形邻域内,Xi与m个最近邻点的欧氏距离均值的倒数,代表了Xi与周围点的紧密度。特征点的紧密度越大,周围类似的匹配点就越多,越适合做类中心点。

利用式(12)计算每一个特征点的紧密度,保留紧密度大于阈值的特征点。将保留下来的特征点的紧密度按降序排列,最大紧密度对应的特征点作为第1个类中心点μ1,取距离μ1最远的特征点作为第2个类中心点μ2,取距离前2个类中心点μ1,μ2距离之和最大的点作为第3个类中心点μ3。据此类推,取距离前i-1个类中心点μ1,μ2,…,μi-1距离之和最大的点作为第i个类中心点μi,至此得到所有类初始中心点。

4.1.2 特征点分组

1) 按上文所述方法,利用式(12)计算所有特征点的紧密度,并确定各类初始中心点{μ1,μ2,…,μk},各类为{C1,C2,…,Ck};

2) 计算其余特征点到各类中心点的欧氏距离,将特征点归入与类中心点距离最小的类中;

3) 再次计算各类中心点,即

(13)

重复2),3),直至各类中心点稳定。

4.2 利用改进的RANSAC算法求取变换模型

经典的RANSAC算法作为一种估算数学模型的优秀算法,从数据集中随机抽取4对匹配点估算变换模型,计算对应的内点。重复选点计算,对应内点最多的变换模型为最优解。但若选取的匹配点距离过近,只会得到局部最优解而非全局最优,只能找到很少的内点,浪费大量时间用于无用计算,增加时间成本。

本文利用改进的K-means算法根据特征点到各类中心点的欧氏距离进行分组,使图像中处于同一区域的点聚集,不同区域的点远离,将特征点分为N组,令RAN-SAC算法从不同组中选取特征点,避免选取的特征点距离过近,导致算法失败。具体算法为先从N组中随机选取6组,再从每组随机选1个点,用前4个特征点计算变换矩阵,后2个特征点预检验变换矩阵[16],以免在错误的模型上浪费大量时间用于计算。

算法步骤:

1) 利用上文改进K-means 算法将特征点分为N组;

2) 从N组中随机选取6组,再从选出的6组中每组随机抽取1个特征点;

3) 将这6个特征点分为{a1,a2,a3,a4},{a5,a6}2组;

4) 用第1组{a1,a2,a3,a4}及其对应的匹配点利用式(11)计算变换矩阵H,第2组{a5,a6}及其对应的匹配点预检验变换矩阵H。若第2组匹配点中至少有一对匹配点满足H,则H作为候选变换矩阵予以保留。

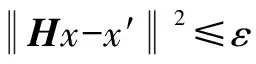
6) 重复步骤2)～5),直至所有的特征点均被选中;

7) 选取内点数最多的候选变换矩阵为最终变换模型。

5 实验

5.1 实验环境和参数

实验环境。硬件环境为Intel®CoreTMi5-9500 3.0 GHz,8 GiB,1000 GiB,软件环境为Windows10,Visual C++6.0。

实验参数。尺度空间中尺度算式为:σn=ωnσ0,σ0=1.5,ω=1.4,n(n=1,2,…,6),σD=0.7σ1。多尺度Harris中k=0.04,Harris阈值为1000,特征匹配r=0.85。相似三角形筛选匹配点中l= 0.05,θ=1°。改进K-means算法中圆形邻域的半径R=35,最近邻点m=20,紧密度阈值为50。RANSAC算法的内点距离阈值ε为1.25。

5.2 测试实验

为验证本文算法的优越性和稳定性,分别利用Harris+RANSAC算法、SIFT+RANSAC算法和本文算法对2组图像进行测试。其中,一组为经过旋转的图像(实验1),另一组为偏差较大、特征较少的图像(实验2)。实验结果如图2、图3和表1所示。

图2 实验1

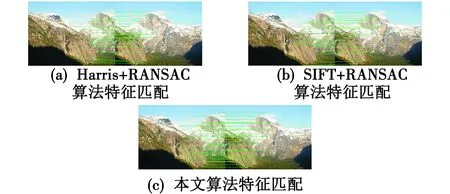
图3 实验2

由测试结果可知,图2中:经典的Harris+RANSAC算法匹配正确率较低,算法性能较差;SIFT+RANSAC算法和本文算法对抗旋转的性能都较好,但SIFT+RANSAC算法提取的特征点数量较多,运算时间较长,匹配正确率一般;本文算法提取特征点数量较少,运算时间和匹配正确率都明显优于SIFT+RANSAC算法。图3中:经典的Harris+RANSAC算法和SIFT+RANSAC算法都有明显误匹配,匹配正确率较低;本文算法特征匹配的误匹配较少,匹配正确率较高,运算时间略长于Harris+RANSAC算法,比SIFT+RANSAC算法短,算法的整体性能优于前2种算法。

5.3 实验分析

本文各部分算法平均耗时为特征提取与粗匹配1.821 s;相似三角形筛选特征点0.85 s,K-means算法特征点分组0.962 s,RANSAC算法计算变换模型0.9635 s。整体算法平均耗时4.635s,平均匹配正确率92.3%。Harris+RANSAC算法平均耗时3.2395 s,平均匹配正确率71.75%;SIFT+RANSAC算法平均耗时5.189s,平均匹配正确率78.55%。

综合分析,本文算法与Harris+RANSAC算法相比,耗时略有增加,匹配正确率有较大提高,与SIFT+RANSAC算法相比,运算时间和匹配正确率都有较大优势。

6 结束语

本文针对现有的多尺度Harris算法运算量大、精度不高的问题,提出一种优化简便算法,为图像建立多尺度空间,Harris算子在尺度空间提取特征点,简化了SIFT特征描述符,用32维向量描述特征,来利用最近邻法进行特征点匹配。利用改进的相似三角形法筛选匹配点,采用改进的K-means算法对特征点分组,将同一片特征点分为一组,使改进的RANSAC算法从图像不同区域选取特征点,得到图像间正确的映射关系,实现配准。最后给出了算法涉及的数据,实验验证了本文算法的性能。