基于自适应多普勒滤波的雷达欺骗干扰抑制

张家林, 吕永胜, 孙殿星, 武星蕊, 韦文斌

(1.哈尔滨工程大学,哈尔滨 150000; 2.青岛哈尔滨工程大学创新发展中心,山东 青岛 266000;3.海军航空大学,山东 烟台 264000)

0 引言

电子战是现代战争的重要组成部分,基于数字射频存储技术(Digital Radio Frequency Memory,DRFM)的欺骗干扰可以在短时间内形成与雷达目标回波高度相干的干扰信号,且当干扰进入雷达天线主瓣后会导致雷达“看不清”、“看不准”,严重影响雷达的作战性能,因此研究其对应的抑制方法具有重大意义。以灵巧噪声干扰[1]和C&I(Chopping and Interleaving)干扰为例[2],都可以在雷达接收端产生大量的假目标干扰[3-4]。

文献[5]通过对信号进行时频分析和反卷积处理来估计干扰信号参数,根据估计的参数重构干扰信号,最后通过迭代对消的方法对干扰进行抑制;文献[6]通过分析C&I干扰时频特征和其对相参雷达的干扰特性,结合快慢时间域处理估计干扰位置、幅度、采样频率和其多普勒频率等参数后重构干扰信号实现对干扰的对消抑制,上述两种方法需要估计的干扰参数较多,且对估计的干扰参数的准确度较为依赖;文献[7]提出一种基于傅里叶变换和分数阶域滤波的方法对灵巧噪声进行抑制,但是该方法对信噪比较为敏感;文献[8]提出了一种捷变频联合Hough变换的抗密集假目标干扰的算法,针对时间不连续的假目标干扰,采用Hough变换和峰值提取实现对目标信号的运动轨迹提取和干扰抑制;文献[9]提出一种基于线性调频(LFM)解线调算法的灵巧噪声干扰抑制方法;文献[10]提出了一种基于多脉冲互补序列和接收滤波器联合设计的抗干扰方法,并针对方法中的非凸优化问题提出了一种基于优化最小化方法的交替迭代算法,但该方法是在获得敌方干扰参数先验信息的前提下开展的研究;文献[11]提出了一种根据估计得到的回波时延截取受干扰的回波段,再通过调制回波段改变不同重复周期内假目标的快时间位置分布,通过相参雷达完成干扰抑制,该方法较为依赖调制信号的参数和个数,如果调制信号较大,则其计算量会大大增加,实时性难以得到保证。

1 干扰特性分析

1.1 C&I干扰特性分析

设雷达发射信号为LFM信号,其零中频时的复数形式为[12]

(1)

式中,k=B/Tp,为调频斜率,B为带宽,Tp为信号脉宽,t为采样时间。

C&I干扰分为Chopping和Interleaving两个阶段[13],在Chopping阶段采用脉冲串对雷达发射信号进行采样,设脉冲串为[14]

(2)

式中:Tc为脉冲信号采样周期;δ(·)为冲击函数;*表示卷积;τ为采样脉宽;b表示从负无穷到正无穷的周期变化。

采样后得到

ji(t)=s(t-ty)p(t)

(3)

式中:ji(t)为采样后的干扰信号;s(t-ty)为干扰机截获的雷达信号;ty为延迟时间。

Interleaving阶段是将抽取到的信号经过调制填充到抽取的空隙中,其表达式为

(4)

式中,G=Ts/τ,Ts为脉冲宽度。根据傅里叶变换性质,ji(t)频域表达式为

Ji(f)=S(f)·P(f)

(5)

式中:f为频率;S(f)为雷达发射信号频谱;P(f)为p(t)的频谱,即

(6)

式中:fc=1/Tc;n表示从负无穷到正无穷的周期变化。根据相位驻留原理[15],当信号TpB≥1时,其频谱S(f)可近似表示为

(7)

由式(4)可知干扰信号频谱为

(8)

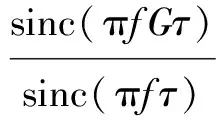
(9)

式中,S*(f)为雷达的匹配滤波器的频率响应函数。由式(9)可以得出,干扰通过匹配滤波后,可以产生与原目标高度相关的假目标。

设干扰机的径向速度为vj,则雷达在干扰机方向接收到的C&I基带干扰信号为[6]

(10)

式中:W为C&I干扰个数;Aw为第w个C&I干扰的幅度;jw为第w个干扰信号;t为采样时间(即快时间);tm为慢时间;tw为干扰的延时;γ为信号波长;fw为干扰机调制的多普勒频率。

脉冲压缩处理后的信号为

(11)

对jcp(t,tm)进行相参积累为在慢时间域对其进行傅里叶变换,设其tw(tm)=tw,fw(tm)=fwtm,则相参积累结果为

(12)

式中,fm表示相参积累后慢时间域频率的变量。由式(12)可得,C&I干扰信号在经过雷达接收机的脉冲压缩和相参积累后在RD域上能量会与目标回波一样获得积累。

1.2 灵巧噪声干扰特性分析

本文主要针对卷积灵巧噪声进行抑制。卷积灵巧噪声干扰由干扰机将截获存储的雷达发射信号与调制信号进行卷积生成,调制信号可以选用噪声或锯齿波。根据信息论,高斯白噪声在平均功率固定的情况下拥有的任意随机波形的熵值最大,所以一般选用高斯白噪声为调制信号。由此得出卷积调制的灵巧噪声干扰的数学表达式为[16]

js=s(t)*ξ(t)

(13)

式中,ξ(t)为标准高斯白噪声。干扰信号经过匹配滤波后的输出信号可以表示为

jsp(t)=js*s*(-t)

(14)

干扰信号频谱为

(15)

式中,N(f)为ξ(t)对应的频谱函数。对式(15)做傅里叶逆变换,可以得到Js(f)的时域输出为

(16)

式中,Js(t)为Js(f)的时域输出。

2 基于YOLOv5的干扰识别

2.1 YOLOv5模型结构

YOLOv5的整体网络结构大致可以分为输入端、Backbone网络、Neck网络和Head输出端4个部分。YOLOv5在Backbone网络中采用了CSPDarkNet53结构,从而在减小计算量的同时保证其识别的准确率。YOLOv5将FPN+PAN模块应用于Neck网络,且通过CSP2结构增加了其特征融合的能力,使其可以提取目标更加全面的深层特征[17-18],从而在低信噪比情况下对较小的目标拥有更好的识别能力。此外YOLOv5还具有更快的识别速度,更加符合干扰抑制的使用场景。

2.2 干扰参数初步估计

信号在经过脉冲压缩和相参积累之后,其干扰的多普勒频率及其时延在RD谱上表现为不同的多普勒通道和距离通道。本文首先通过识别锚框(在目标检测任务中进行预测的像素框就是锚框)的位置坐标及其RD谱的坐标的比例关系来对干扰和目标的多普勒频率进行大致估计,得出干扰信号的一个初步位置范围。其多普勒频率转换式为

fdmax=(ymax-ymaxpos)/(ymax-ymin)·fl

(17)

fdmin=(ymax-yminpos)/(ymax-ymin)·fl

(18)

其中:ymax和ymin分别是多普勒域坐标轴对应的锚框位置的最大值和最小值;ymaxpos和yminpos分别为识别结果锚框对应的位置在多普勒域的最大值和最小值;fl为整个多普勒域的量程。

3 自适应多普勒干扰抑制

3.1 基于量测信息的精确估计

在上述初定位的基础上对干扰的多普勒频率进行精确估计。根据上述的初步估计,利用门限及均值函数对干扰信号参数进行精确估计。

C&I干扰及灵巧噪声干扰与雷达信号具有很强的相关性,在经过脉冲压缩及其相参积累后,根据最大信噪比原则可得干扰相对噪声有较强增益[19]。相关公式在此不再赘述。

图1为当信噪比为-15 dB时接收信号经过脉冲压缩和相参积累后的RD谱图。

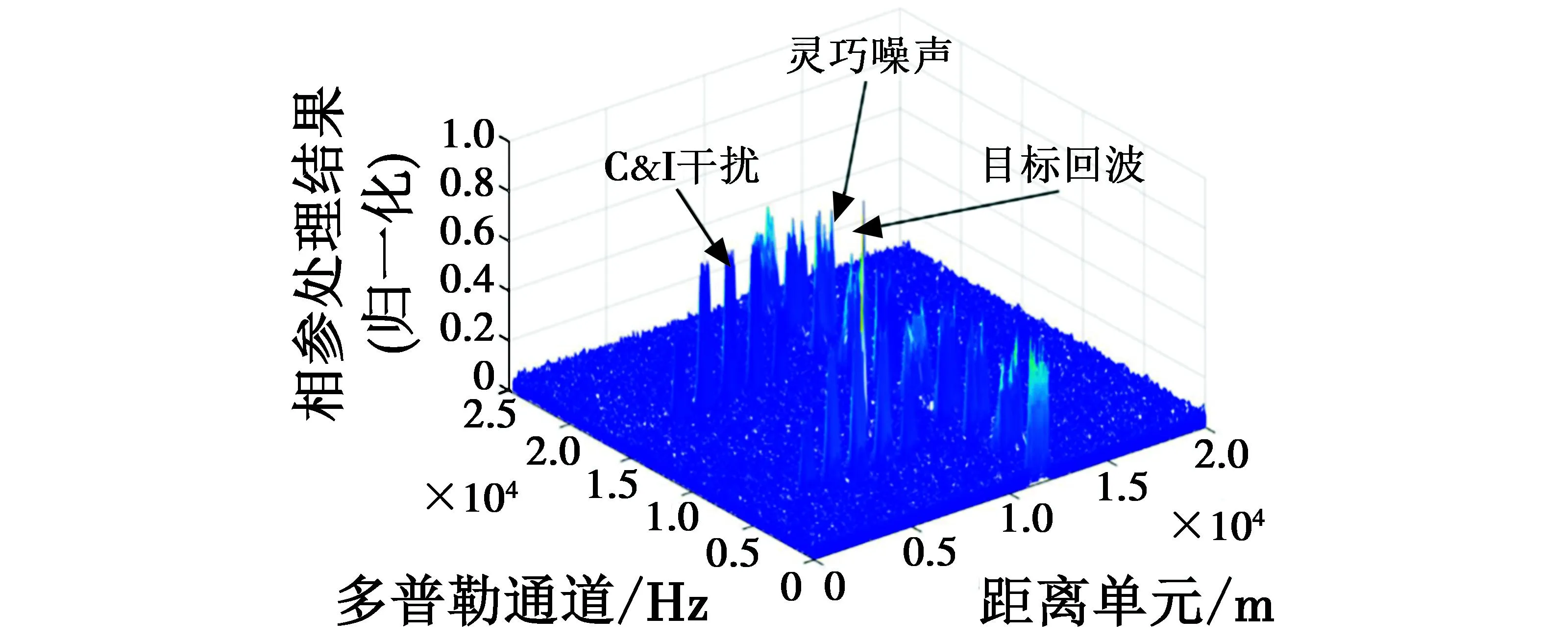
图1 接收信号RD谱图

由图1可以看出,即使在信噪比十分低的情况下,目标回波、C&I干扰和灵巧噪声干扰的幅值依然明显大于噪声。

通过采集无发射信号状态下的噪声信号,对其进行脉冲压缩和相参累计。为减小误检概率,本文以其峰值的3倍作为检测判定门限F,并依照从左到右、由上到下的顺序进行门限检测。在检测多普勒频率时,在相同多普勒通道,对不同距离门限的信号幅值进行求和平均;最后搜索均值的峰值,实现对回波和干扰的粗略定位。

由于在进行多普勒频率的估计时,受其脉冲数量的限制,对其估计的误差相对较大,故本文采用局部内插法,实现精细定位。在上述RD谱定位处,取出其对应的RD域谱切片,对每个频率点处的幅值利用二次多项式进行拟合,进而对其进行精细化内插。为满足系统对多频率估计的精度要求(速度精度为1 m/s),其在多普勒频率处内插值Ni应满足

Ni>2faN/FPRF

(19)

式中:fa为雷达发射信号的载频;N为相参积累脉冲个数;FPRF为脉冲重复频率。

最后依照门限进行搜索,对其多普勒频率及其距离门进行精确估计。

3.2 自适应欺骗干扰抑制

基于上述干扰识别结果和参数估计信息,当干扰与目标的多普勒频移不重叠时,本文提出改进基于数字综合算法的FIR滤波器组的MTD实现方法,在干扰的频率(即多普勒频率)处形成较深的零陷,从而抑制干扰并滤除噪声信号。

设多普勒滤波器的输入信号为X=S+Xn。其中:S表示慢时间域期望信号,采用向量表示;Xn为噪声和待抑制干扰信号在慢时间域的矢量。设滤波器组权矢量为W(n)=[W1(n),W2(n),…,WN(n)]T,其中,Wi(n),i=1,2,…,N,为第i个滤波器的权矢量。

慢时间域期望信号为

S=(s1,s2,…,sn,…,sN)T

(20)

sn=Aeiω(n-1)Trn=1,2,…,N

(21)

其中:A为包含幅度的复系数;ω为期望信号多普勒频率;Tr为信号重复周期。

滤波器对信号进行滤波处理后的结果[20]Y为

Y=Wi(n)S+Wi(n)Xn

(22)

则输出的期望信号功率和杂波的功率比[21]为

(23)

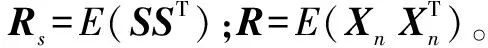
现假设SNJ最大,设R为正定矩阵,则R=R1/2·R1/2。插入中间变量β=R1/2Wi(n),则SNJ可写为

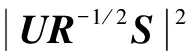
(24)

式中,U=β/β,为归一化单位向量。

由此可得,当β=R-1/2S时SNJ最大。最后得

Wi(n)=R-1S。

(25)

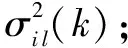
(26)

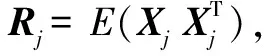
然后,根据式(25)得出滤波器的权矢量Wi(n),再根据权矢量求滤波器在整个多普勒频段的频率响应,即

(27)

此时,根据主瓣峰值h(f)与上文设置的衰减程度,求频率响应在待抑制干扰频率和副瓣处所期望电平值d1,d2,即

(28)

得到的电平值是滤波器在待抑制干扰多普勒频率区域和副瓣区域期望的幅频响应幅值。之后根据待期望幅频响应和真实幅频响应的差值来更新虚设干扰的功率值,以此实现滤波器权数的迭代更新。下一次迭代虚设干扰各频点的功率为

( 29)

式中:[ffl,ffr]为滤波器主瓣区域;[fjl,fjr]为待抑制干扰区域;其他为副瓣区域;μij(k)和μil(k)分别为

(30)

(31)

其中:H(k,fl)为第k次迭代fl频点的功率值;K为迭代增益。之后进入下一轮的迭代,直至期望幅频响应和真实幅频响应相同或迭代次数达到上限。

自适应多普勒滤波器流程如图2所示。

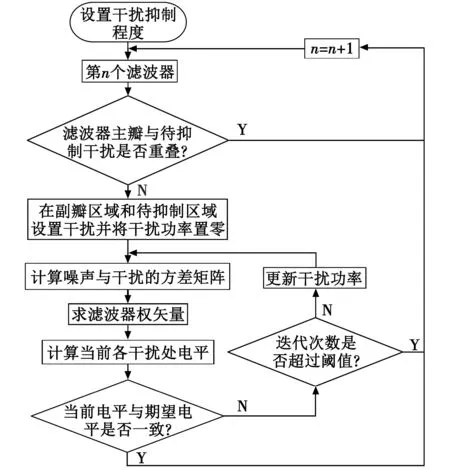
图2 自适应多普勒滤波器流程图

假设原始接受信号的RD矩阵可以表示为F(t,f),根据多普勒滤波器组处理过后的信号G(t,f)可以表示为

(32)

式中,fij为其待抑制干扰信号的多普勒频率。

在信号经过多普勒滤波器组的处理之后,为了减少图像识别的次数,本文根据抑制后的结果设计一个干扰参数监测系统。因为密集假目标数量较多,所以在有密集假目标的多普勒通道中,信号的起伏程度相对无干扰信号的状态下较为剧烈,导致有密集假目标的多普勒通道的信号方差值与无干扰的多普勒通道的信号方差值相比具有很大差异,因此,本文通过方差检验来判别其干扰是否发生改变。

不失一般性,本文假设输入噪声为高斯白噪声,根据I/Q双通道测量原则,则有对应的I通道信号nI和Q通道信号nQ。输入噪声为

n(t)=nI(t)+j·nQ(t)

(33)

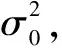
根据上文分析构建相应的方差检验统计量χ2为

(34)

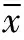
(35)

xi为集合Va中的样本。假设H0为总体方差为σ2成立,从而得到干扰变化判别准则为

(36)

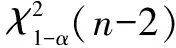
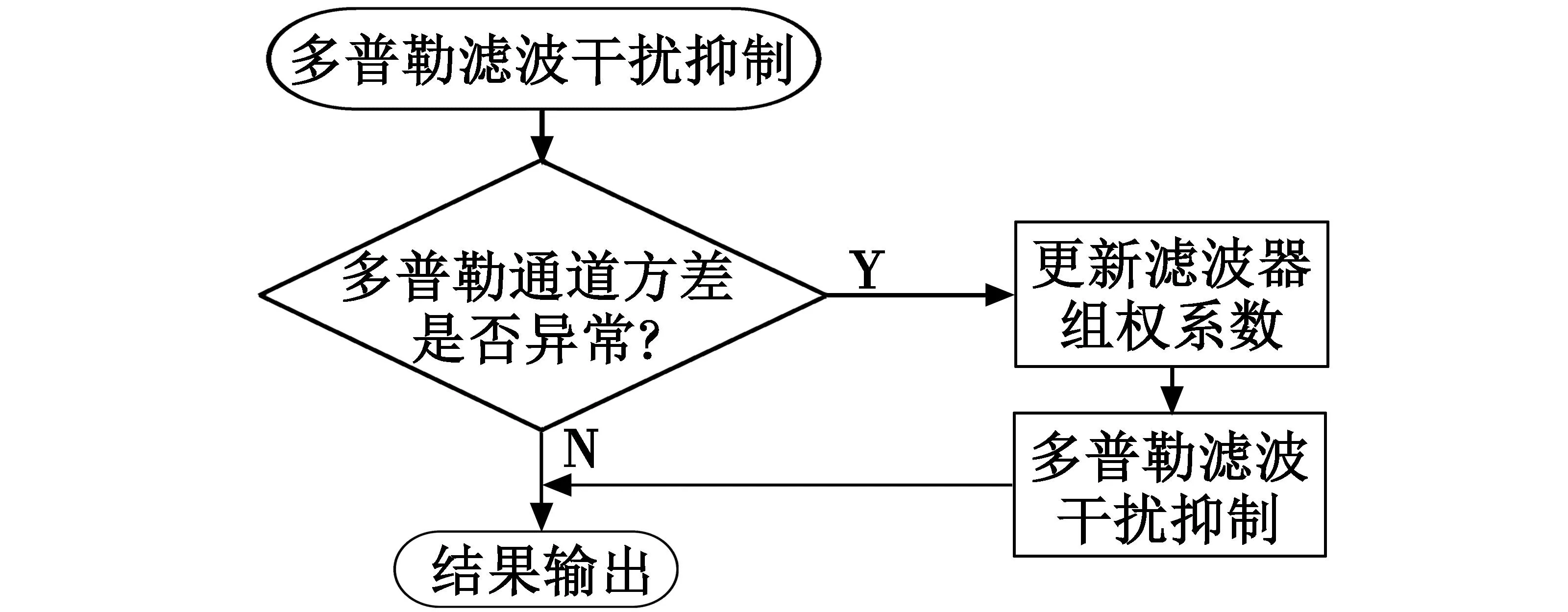
图3 自适应干扰抑制流程图

4 仿真验证

4.1 参数设置

为验证本文所提方法的有效性,设置以下仿真实验进行验证,雷达的各参数如表1所示。

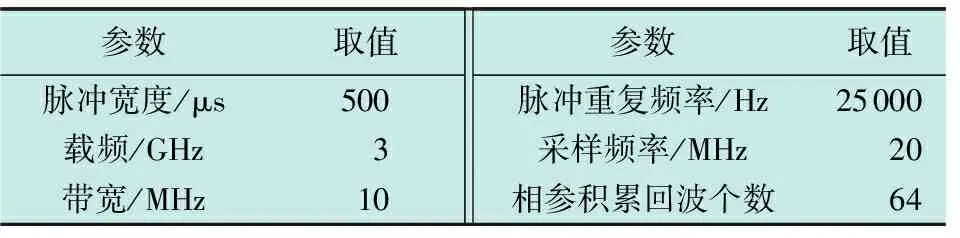
表1 雷达仿真参数

本文所抑制的密集假目标干扰主要是C&I干扰和灵巧噪声干扰。目标及其各参数如表2所示。

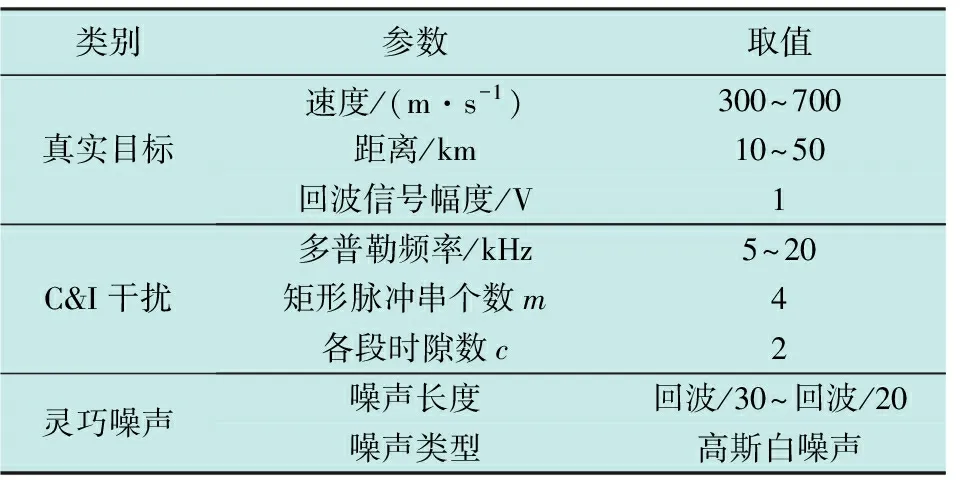
表2 目标及其干扰仿真参数

不失一般性,本文加入高斯白噪声作为其噪声信号,信噪比为-10～15 dB。

4.2 干扰识别仿真

本文中的数据集为目标回波信号、C&I干扰和灵巧噪声干扰随机排布进行处理,其位置、多普勒频率等参数都为在4.1节的给定范围中随机产生的。同时,为了使产生的密集假目标信号与其实际场景类似,单类干扰分量的干噪比设定为-15～0 dB。设置训练数据集为600张,测试集数量为100张。最终识别效果如图4所示。

图4 识别效果图

由图4可以看出:当信噪比超过-8 dB时,干扰的识别率可以达到97%以上,且目标回波的识别率可以达到100%,有较好的识别效果。当信噪比高于-6 dB时,本文所提方法对两种干扰的识别率都可以达到100%。由此可见,本文所提方法对雷达有源复合干扰是有效可行的,相比于文献[22],C&I干扰在0 dB信噪比时的识别率高出39%,保证了后续参数初步估计的准确性。

4.3 参数估计仿真

由干扰识别给出的锚框所确定信号时延及其多普勒频率所在的大致位置,并且根据上文分析与对应的公式转换,可以得出其RD信息所在的局部范围,显著减小在参数估计时的计算量。转换结果如表3所示。

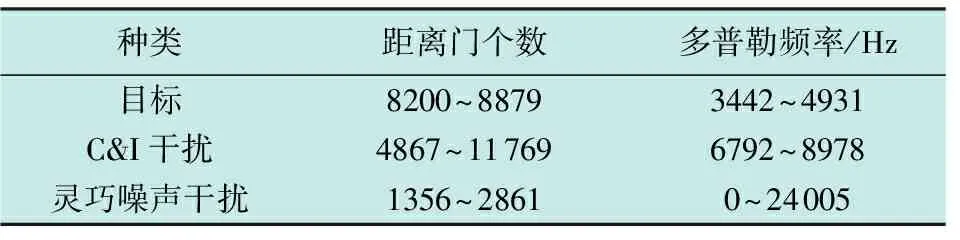
表3 参数初步估计结果

本文计算检测后的多普勒频率的绝对误差为

(37)

式中:Xi为第i次实验的估计结果;Yi为第i次实验对应的真实值;M为实验的次数。

实验结果如图5所示。

图5 多普勒频率误差分析

设置信噪比分别为5 dB,0 dB,-5 dB,-10 dB,进行400次蒙特卡罗实验,为保证其随机性,在实验过程中从随机数区间中随机抽取距离门和多普勒频率的值。由图5可以得出,当信噪比大于0 dB时,多普勒频率估计绝对误差逐渐趋于稳定,并保持在50 Hz,误差值小于速度分辨率。

4.4 干扰抑制仿真

本文设MTD滤波器组的阶数为64,滤波器总数为64,设置C&I干扰多普勒频率分别为5105 Hz和14628 Hz、灵巧噪声卷积噪声长度为雷达信号长度的1/20,仿真结果如图6所示。

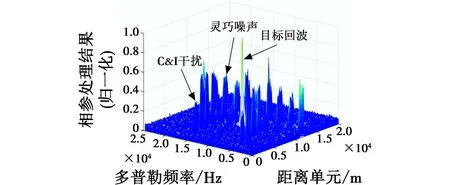
图6 回波信号RD图

从图6仿真结果可以估计出,其灵巧噪声干扰的多普勒频率为2387 Hz,5058 Hz,7431 Hz,10087 Hz,12513 Hz,14900 Hz,17557 Hz,19906 Hz和22601 Hz,估计出的C&I干扰的多普勒频率为5060 Hz和14596 Hz。根据估计出的多普勒频率设计其MTD滤波器组,最终滤波器组的幅频响应如图7所示。

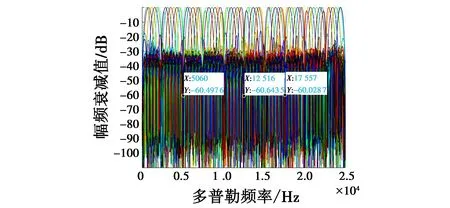
图7 滤波器组幅频响应

由图7可以看出,滤波器在干扰的频率点处均存在-60 dB的衰减。原始回波信号通过上文设计的滤波器组得到最终抑制结果,最终的RD图见图8。

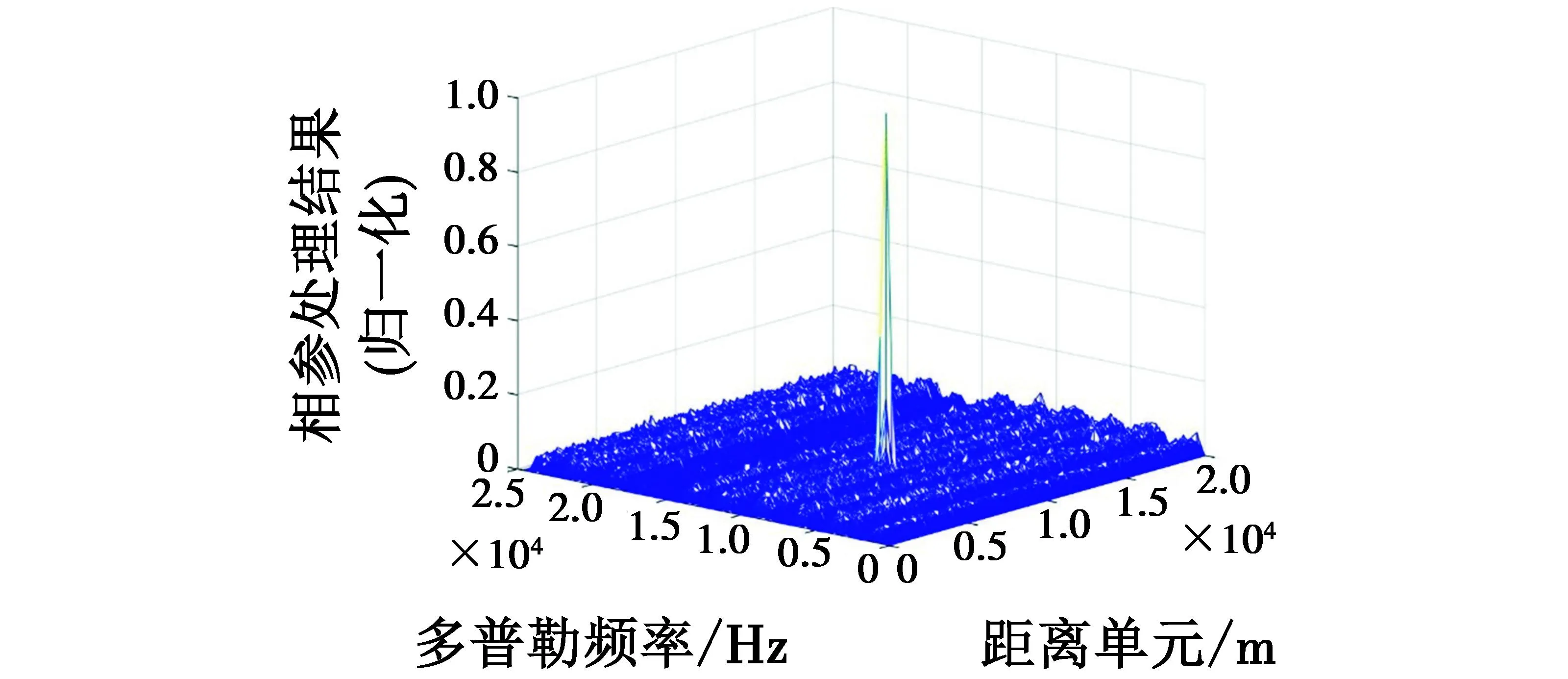
图8 最终抑制结果

由图8和图6对比可得,干扰抑制后,目标在RD图中明显突出,灵巧噪声与C&I干扰都得到了有效的抑制。

现假设下一个CPI的干扰参数发生变化,若多普勒滤波器的参数不进行更新,抑制结果如图9(a)所示。

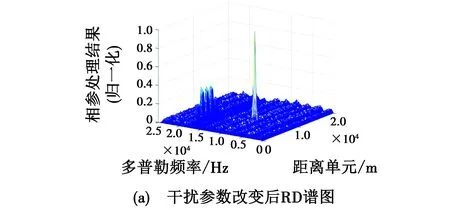
图9 仿真结果

由图9(a)可以看出,干扰并未得到完全抑制。仿真其多普勒通道方差可以看出其多普勒通道的方差波动较大,如图9(b)所示。可以看出,其在第41个多普勒通道的幅值的方差出现了剧烈的变化,此时重新进行干扰识别和参数估计以校准多普勒滤波器,如图9(c)所示。可以看出,经过校准后的滤波器组处理后的信号的多普勒通道的方差值再次进入稳定。

5 结束语

本文提出了一种基于自适应多普勒滤波的干扰抑制方法。首先,通过提取回波信号的RD图像,利用YOLOv5识别干扰类型并对参数进行粗略估计;然后,利用二维重构和插值法对干扰参数进行精细估计;最后,根据估计得到的参数设计多普勒滤波器组对干扰进行抑制处理,利用抑制后的信号构建检验统计量,利用方差检验判别是否需要更新多普勒滤波器权重,实现自适应调节。仿真实验验证了所提方法的有效性,在信噪比大于-8 dB时,对干扰的正确识别率达到99%以上,多普勒参数估计误差小于65 Hz;最终利用设计的多普勒滤波器,对干扰进行了有效抑制。本文针对的是干扰和目标回波多普勒频率不同时的情况,而当干扰和目标回波的多普勒频率交叠时本文方法便不再适用。后续将进一步研究如何在干扰和目标回波交叠时对干扰进行抑制。