基于改进遗传算法的舰载机弹药挂载调度
2024-01-15吕晓峰杨东泽郑晓梅
吕晓峰, 杨东泽, 马 羚, 郑晓梅
(海军航空大学岸防兵学院,山东 烟台 264000)
0 引言
航母作为海上作战平台,需要为舰载机提供各种保障工作,其中弹药挂载是舰载机保障的重要内容之一。舰载机弹药转运至航母甲板后,待舰载机允许进行弹药挂载工作时,需将每架舰载机所需的弹药快速、有序地挂载到位。弹药挂载作为舰载机弹药保障的最后一个环节,作业时间较长,且弹药数量较多,挂载方案复杂。目前,弹药挂载方案基本依靠人力计算,计算时间较长,在舰载机日常训练与战时作战过程中多机、多波次循环出动的背景下,得到的调度方案难以满足时效性和稳定性要求。因此,在考虑舰载机弹药保障时,弹药挂载工作作为重要一环对舰载机保障效率的提高具有重要意义。
目前,国内外针对舰载机弹药挂载调度的研究较少,大多数是对完整的舰载机弹药保障进行研究。张洪亮等[1]基于满足任务所需的弹药数量约束条件,以任务完成时间最短为优化目标建立舰载机弹药调度模型;马登武等[2]根据建立的舰载机弹药调度模型求解了武器升降机转运弹药以及将弹药转运至各个停机位的调度方案;陶俊权等[3]以弹药转运车为基础运输单元建立模型,求解了武器升降机与弹药转运任务的分配方案;夏国清等[4]在考虑到调运系统不确定条件下的情况,运用T-S模糊非线性优化方法优化弹药调度方案;史文强等[5]对航母飞行甲板作业进行了梳理,分析了作业流程与时间分配。上述研究都是将弹药挂载工作并入整个弹药保障进行考虑,根据国外先进航母经验,由于训练和作战过程中舰载机机群多机、多波次循环出动的需求,在该背景下弹药保障会受到飞机起降工作的影响,使得弹药从甲板下弹药舱至舰载机机位的保障流程不能时刻保持畅通。在实际保障中,舰载机所需的大部分弹药是从甲板缓冲准备区转运至舰载机战位,因此研究舰载机的弹药挂载调度问题时需将其从整个弹药保障工作中独立出来。对于调度问题的求解方式多种多样,在实际中应用较为广泛的有禁忌搜索算法[6-7]、模拟退火算法[8-9]、遗传算法[10-11]、蚁群算法[12]以及粒子群算法[13]等优化算法,其中,遗传算法全局搜索能力较强,具有较强的鲁棒性,适合求解复杂的优化问题[14-16]。
基于以上分析,本文结合舰载机弹药挂载工作的实际保障流程,建立了弹药挂载调度模型,并对遗传算法进行改进,以提升算法性能,最终能够得到高效的调度方案。
1 舰载机弹药挂载调度模型
1.1 问题分析
在考虑舰载机弹药挂载调度问题时需要考虑以下几点。
1) 舰载机弹药从甲板缓冲准备区转运至舰载机战位过程中,是以弹药转运车为载体进行运输,在舰载机弹药挂载调度时实际上是对弹药转运车的调度,因此在弹药挂载调度时以弹药转运车为单位进行调度。舰载机执行作战任务时会挂载不同型号的弹药,会根据弹药的大小匹配不同类型的弹药转运车,其中,某些类型的弹药转运车可同时携带多枚弹药,这会给弹药挂载调度方案增加复杂度。
2) 舰载机在挂载弹药时会受到挂弹空间约束,在进行弹药挂载时,机翼同侧会受到空间限制而不能同时挂载2枚弹药。
3) 舰载机的保障工作除了弹药挂载工作之外还有众多其他保障工作,因此在对多架舰载机进行弹药挂载时各架舰载机的起始挂载时间会有所差异。
1.2 模型建立
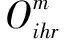
由于各架舰载机的弹药挂载起始时间并不完全相同,可能会出现个别舰载机弹药挂载起始时间较晚的情况,若以最小化最大完工时间为优化目标,则针对弹药挂载起始时间较早的舰载机,其完工时间也会较早,难以找到其最优的弹药挂载方案。因此设置所有舰载机弹药挂载时间之和为优化目标,即
(1)
约束条件为
(2)
(3)
(4)
(5)
(6)
(7)
(8)
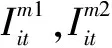
2 算法设计
由于舰载机的弹药挂载需求不同,若按照未改进的遗传算法进行交叉和变异操作会产生大量不可行解,影响算法的求解效率。针对该问题,对遗传算法进行改进,提出一种基于染色体片段的编码操作,并基于染色体片段进行交叉与变异操作,以提高算法的收敛速度。
2.1 编码
在保障多架舰载机弹药挂载工作时,不同的舰载机弹药需求不同,即对舰载机保障的弹药转运车不同。若按照以往的随机编码方式则会造成大量的不可行解,需要对生成的编码进行调整。在编码时,本文为避免上述情况的出现提出了一种基于染色体片段的编码方式:根据舰载机的数量生成多个染色体片段,每个片段为该舰载机所需弹药来源,如图1所示,片段1表示第1架舰载机所需的4枚弹药分别由第1,3,9和10辆弹药转运车提供,依此类推。

图1 染色体编码示意图
2.2 解码
算法的解码操作是将求得的解转换为一个可执行的调度方案,实现染色体与舰载机弹药挂载方案之间的映射,对于本文所研究的问题,需要确定保障舰载机的弹药转运车开始工作时间和结束时间。按照染色体片段顺序依次对其进行解码,同样,片段内也是依次对基因进行解码,并规定在舰载机机翼两侧都具备挂载条件时优先挂载左侧机翼,依次从片段中的编码值开始解码。
解码步骤如下。
Step 1 若该编码值代表的弹药转运车为首次挂载弹药,则需经过缓冲准备区至挂载区的转运时间t0,并判断此时该舰载机机翼两侧有无挂弹任务,若一侧空闲则可直接挂载,否则需等待至在两侧中任务优先的一侧开始挂载。
Step 2 若该编码值代表的弹药转运车从其他机位转运过来,则需经过机位间转运时间TS,iec,同理并判断此时该舰载机机翼两侧有无挂弹任务,若一侧空闲则可直接挂载,否则需等待至在两侧中任务优先的一侧开始挂载。
Step 3 其他片段重复Step 1和Step 2的操作。
2.3 适应度函数
评价调度方案好坏的标准就是适应度值的大小,结合建立的舰载机弹药挂载调度模型,根据目标函数将适应度函数设为
fitness(i)=f。
(9)
2.4 选择算子
本文在选择染色体时采用了轮盘赌选择方法,该方法操作简单,也是遗传算法常用的选择算子。轮盘赌选择操作根据个体染色体适应度值在种群染色体适应度值总和的比例,依次确定该染色体被选中的概率,即适应度值比例法。选择方式为
(10)
式中,pi(i)表示染色体被选择的概率。
2.5 交叉算子
算法设计中的交叉方式主要包括单点交叉、多点交叉和部分匹配交叉等[17],在进行上述交叉操作时,染色体的编码会发生变化,由于给舰载机提供弹药的转运车并不相同,并且还需受到弹药转运车上携带弹药数量的约束,因此考虑到上述情况,提出了基于染色体片段的交叉方式,将编码中的片段视为一个整体,可缩小交叉位置的范围,并避免了不可行解的发生,提高了算法的搜索速度,图2为染色体的交叉操作示意图,图3为交叉后染色体调整示意图。
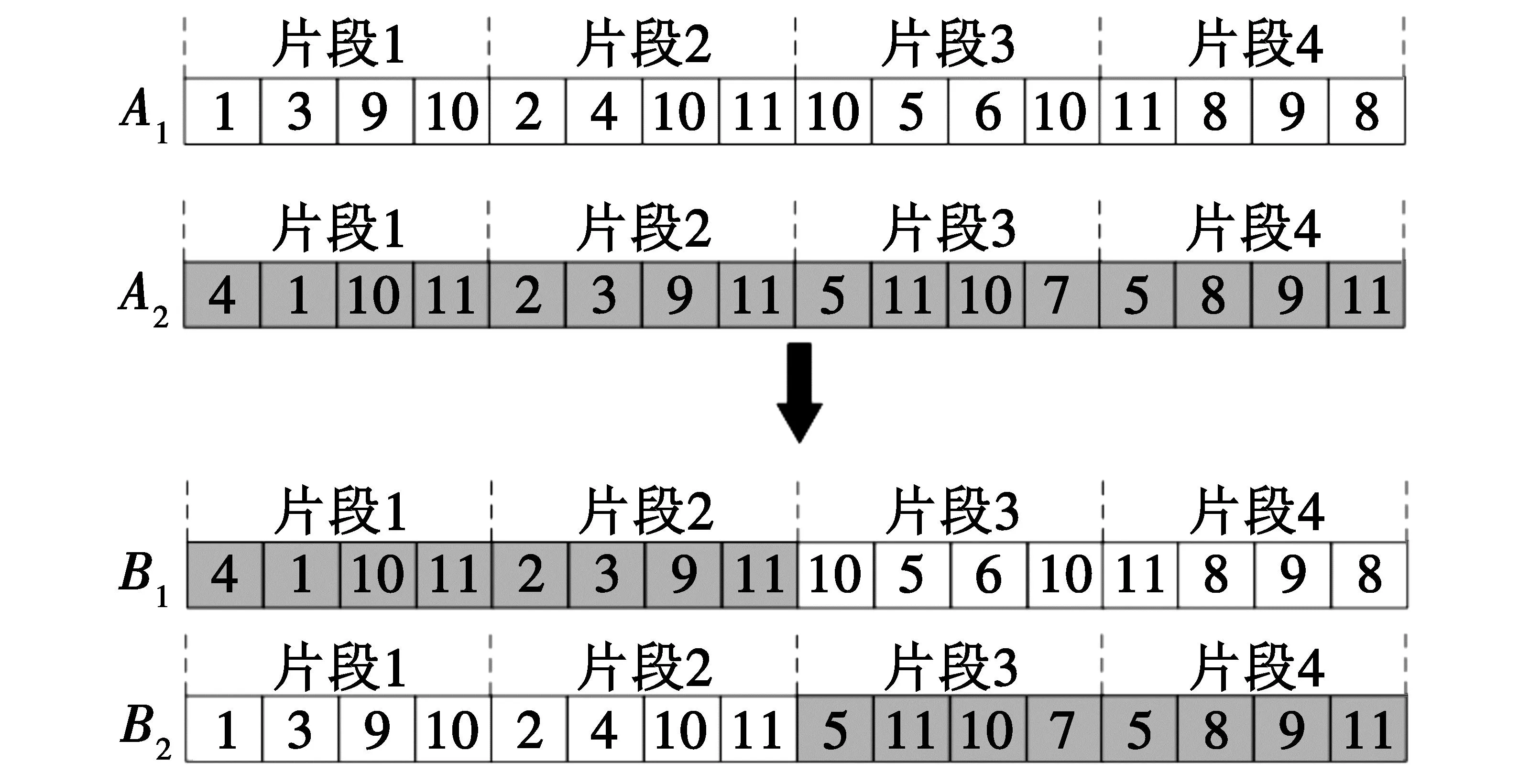
图2 染色体交叉操作示意图
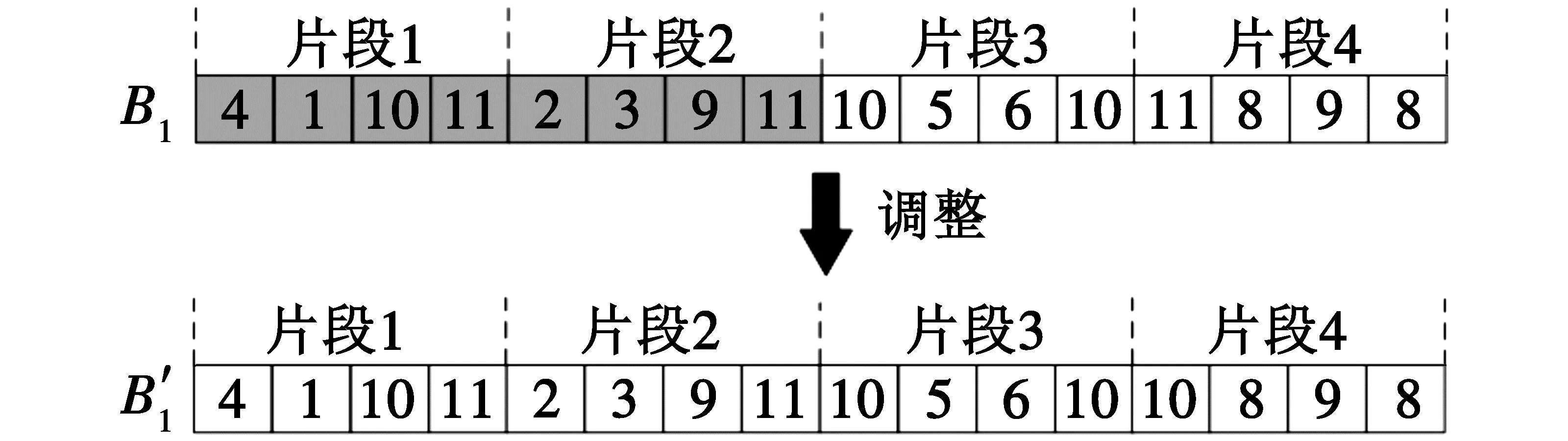
图3 染色体调整示意图
具体操作方法如下。
Step 1 令交叉概率为p1,随机生成α(0≤α≤1),设参加交叉操作的两个父代个体分别为A1和A2。若α≥p1,则进行Step 2,否则直接进行变异操作。
Step 2 生成片段选择参数b(b∈[1,nn]),nn为染色体片段数量,通过参数b确定染色体的交叉点s1。
Step 3 将A2的前s1片段与A1的后nn-s1片段进行组合形成子代个体B1,同时将A1的前s1片段与A2的后nn-s1片段进行组合形成子代个体B2。
Step 4 染色体交叉后弹药转运车提供弹药的数量会发生变化,如图2中染色体A1中第10辆弹药转运车提供4枚弹药,第11辆弹药转运车提供3枚弹药,而交叉后第10辆弹药转运车提供的弹药数量少了1枚,而第11辆弹药转运车提供的弹药数量多了1枚,需针对该情况进行调整(见图3)。
2.6 变异算子
通过变异算子可提高算法的全局搜索能力,维持种群的多样性,并对交叉搜索功能起到辅助作用。遗传算法在寻找最优解时较易陷入局部最优,为了增强算法的局部搜索能力,在迭代的前期设置较小的变异率更有利于较优个体的保留,在迭代的后期设置较大的变异率有利于避免种群的“早熟”。因此,本文采用了自适应变异率,迭代至第k代的变异率为
p2=l1+l2×(k/Ncg)
(11)
式中:l1为设置的最小变异率;l2为设置的最大变异率;Ncg为算法最大迭代次数。
由于随机变异生成的染色体不再满足弹药转运车上携带弹药数量的约束,本文设计了基于染色体片段的变异操作,图4为染色体变异操作示意图。
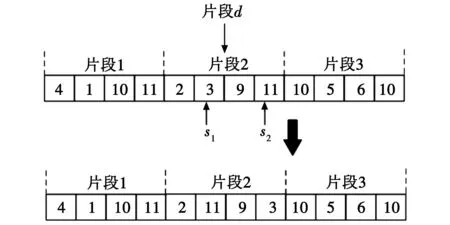
图4 染色体变异操作示意图
具体操作方法如下。
Step 1 根据迭代次数生成变异概率p2,随机生成β(0≤β≤1)。若β≥p1,则进行Step 2,否则跳过变异操作。
Step 2 生成片段选择参数d(d∈[1,nn]),nn为染色体片段数量,通过参数d确定染色体的变异片段位置,并随机生成变异点位置数值s1和s2,其中变异点位置数值s1和s2需小于该片段中的基因数。
Step 3 在染色体片段d中交换变异点s1和s2两处的基因。
2.7 算法流程
本文提出的改进遗传算法流程,具体步骤如下:
Step 1 设置算法基本参数,包括种群数量、迭代次数、交叉率和变异率,并根据本文设计的编码方式进行染色体编码;
Step 2 根据式(9)计算初代适应度值;
Step 3 运用轮盘赌选择方法选择染色体,并按照本文设计的交叉和变异操作对种群进行迭代更新;
Step 4 若达到算法终止条件则输出种群中的最优方案,否则转至Step 3。
3 案例分析
本文以某航母为例,在本次弹药挂载工作中同时保障6架舰载机,需挂载的弹药有3种,对应3类弹药转运车。本次弹药挂载工作中各舰载机的弹药需求见表1,弹药转运车携带的弹药数量以及转运时间见表2。

表1 各舰载机的弹药需求
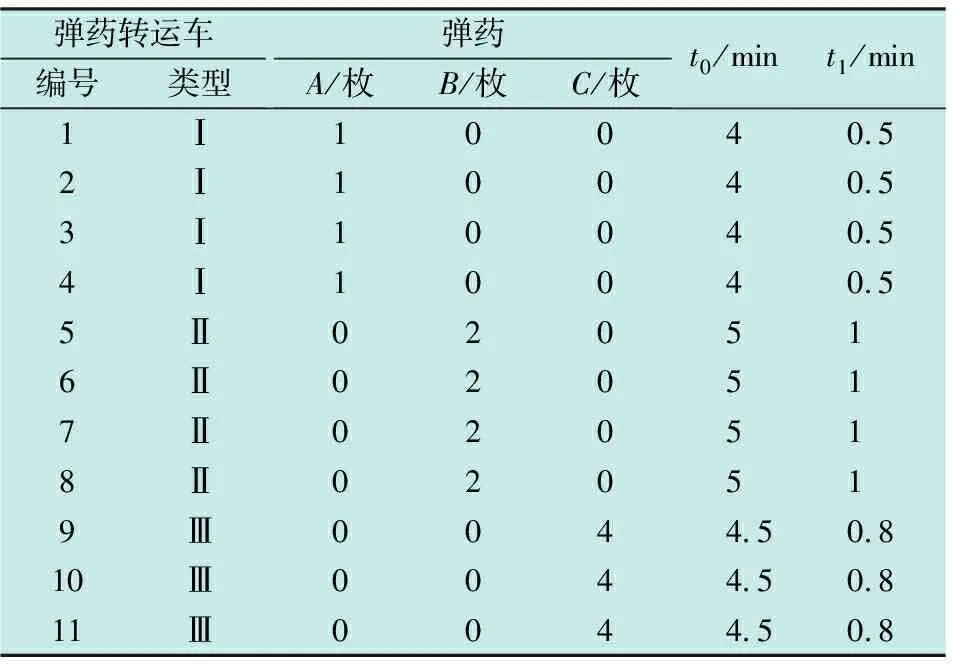
表2 弹药转运车携带的弹药数量以及转运时间
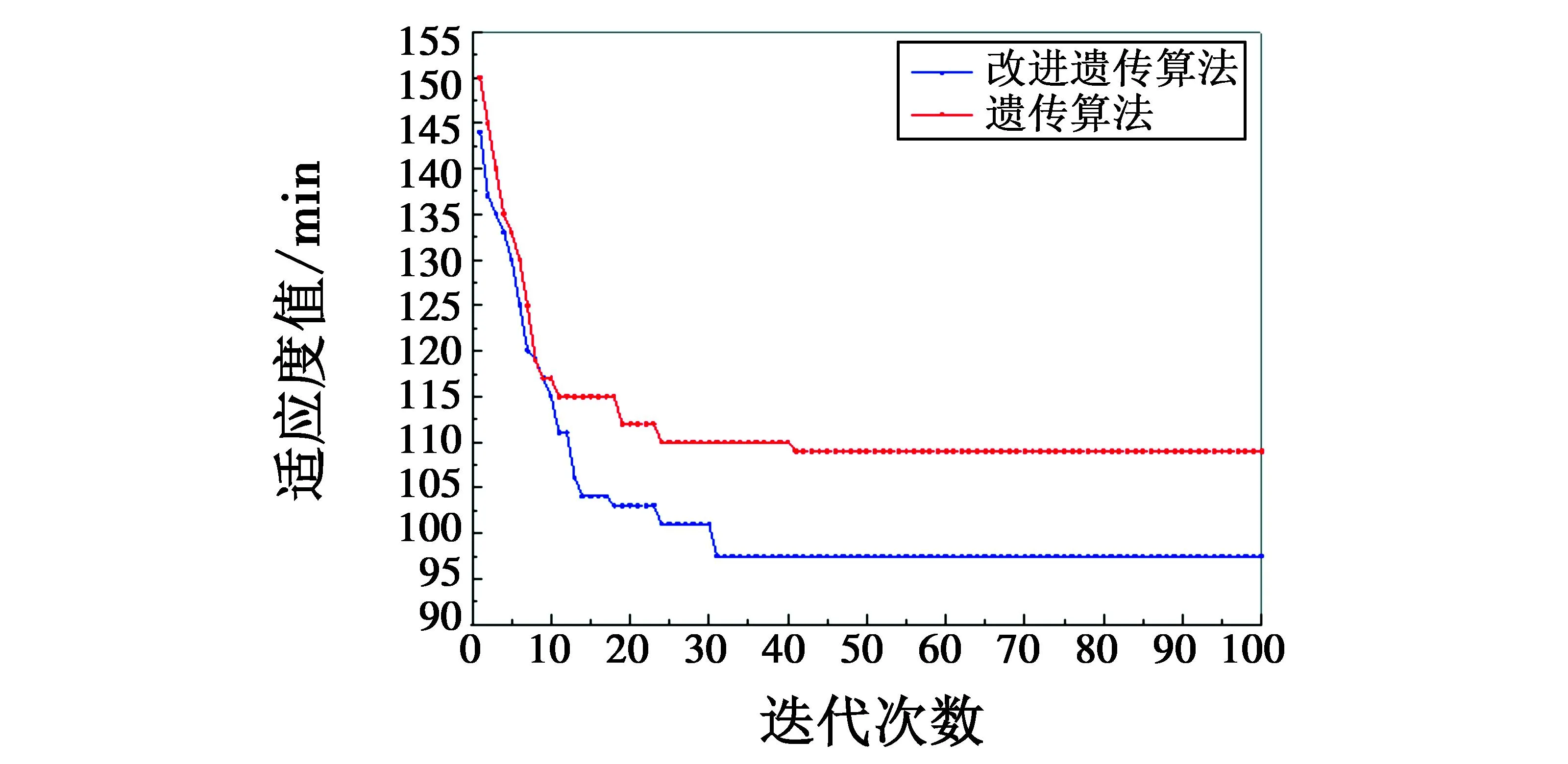
图5 改进遗传算法与遗传算法迭代过程
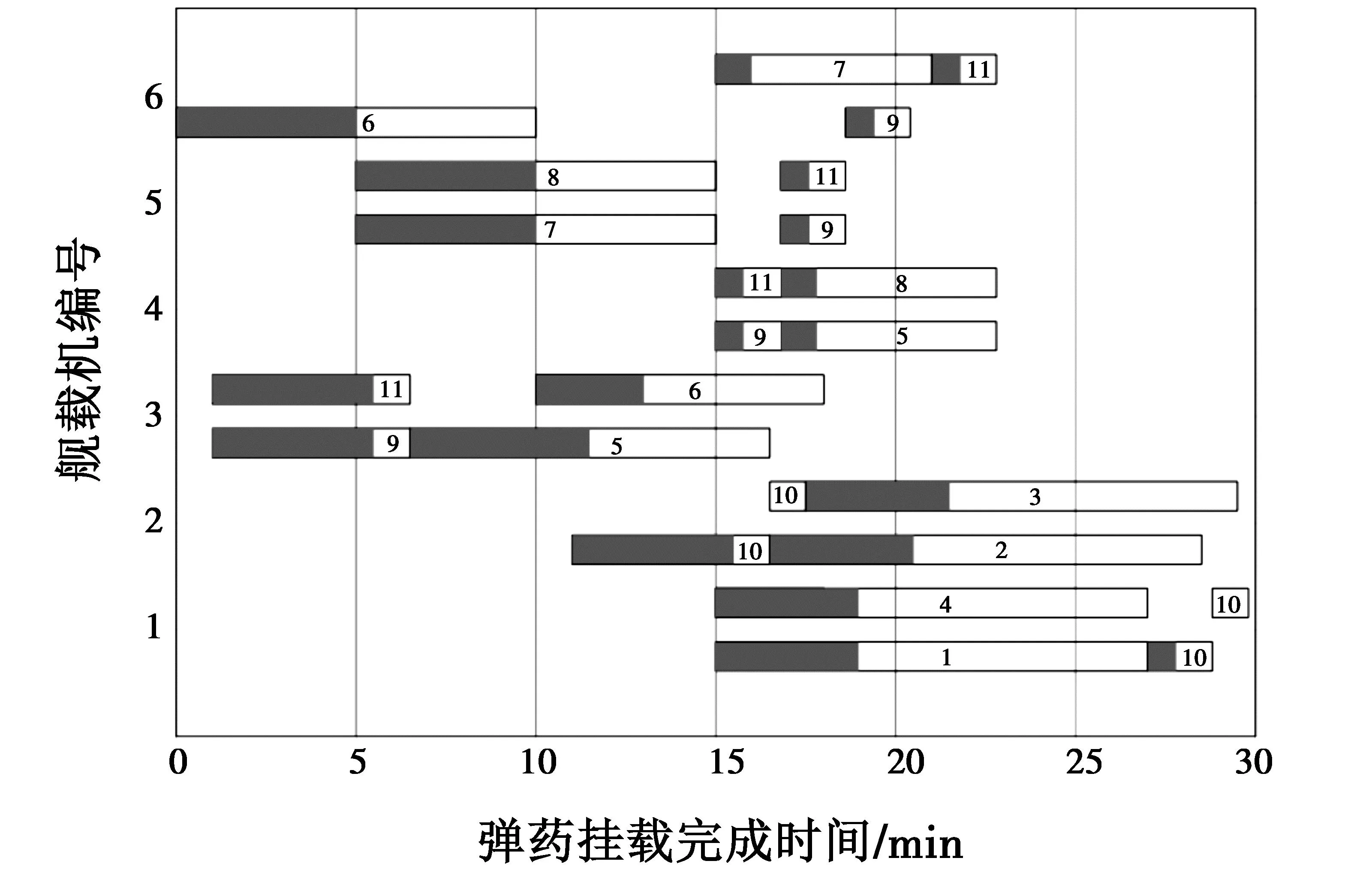
图6 舰载机弹药挂载甘特图
根据图5可看出,改进的遗传算法在迭代至31代时收敛至最优解,而遗传算法迭代至41代收敛至最优解,改进的遗传算法收敛速度更快,并且改进遗传算法最终最优解可达到97.5 min,而遗传算法最终最优解为109 min,说明改进遗传算法搜索能力更强,更有利于避免算法“早熟”的情况发生。图6中数值表示弹药转运车编号,每架舰载机的两行甘特图对应机翼两侧的弹药调度方案,灰色部分表示弹药转运车机位间转移时间。
4 结束语
本文针对舰载机弹药挂载调度中通常忽略的约束问题,建立了舰载机弹药挂载调度模型,该模型以所有舰载机弹药挂载时间之和为优化目标,考虑了舰载机起始挂载时间不同和弹药挂载空间约束条件,提出了一种基于染色体片段编码的改进遗传算法以求解该问题,并采用自适应变异率对变异算子进行改进,获得了更优的舰载机弹药挂载方案。然而,本文所建立的模型仅是考虑各种设备正常工作的状态,若设备发生故障,如何给出实时调度方案是下一步的研究方向。
