基于扰动流体与TD3的无人机路径规划算法
2024-01-15陈康雄
陈康雄, 刘 磊
(河海大学,南京 211000)
0 引言
近年来,无人机由于其快速部署和可控机动性,在围捕[1]等方面得到了广泛应用。然而,如何使得无人机在未知环境下,避开障碍物安全地到达终点成为研究人员的热门研究课题,这是无人机安全并且高效完成任务的重要前提[2]。面对复杂的未知环境,研究人员提出很多路径规划方法,最常见的方法有A*[3],RRT[4],Kino-dynamic RRT*[5]等,然而,这些基于模型的解决方案很难应用于不确定的环境。
为克服上述问题,近年来基于学习的路径规划方法受到了极大的关注。强化学习(RL)[6]算法通过智能体与环境交互从而获取行动策略,换句话说,RL算法独立于环境模型与先验知识之外。之后DeepMind创新性地将深度学习(DL)算法与RL算法相结合,形成深度强化学习(DRL)算法,DRL算法将高维输入转换为更真实的低维状态,其中,深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG)算法的连续性被广泛用于路径规划,但其面对复杂的环境收敛性往往不稳定,因而,FUJIMOTO等[7]提出TD3算法。近年来,有学者提出了Soft Actor Critic (SAC)[8]算法,即在Actor-Critic框架下引入了熵的技巧,进而提升动作选取的随机性。XIAO等[9]通过SAC算法来训练无人机穿过倾斜的狭窄缝隙,并将学习到的策略成功地应用于真实环境。
文献[10]验证扰动流体动态系统(Interfered Fluid Dynamic System,IFDS)[11]与DDPG融合的算法相比于单独的IFDS算法在路径规划上的优势。
1 无人机航迹规划系统模型
为了满足无人机路径规划任务中避障的实时性,并保证航迹的平滑度,本文提出了基于扰动流体与TD3算法的无人机路径规划算法,图1所示为其系统模型。
无人机路径规划系统模型搭建过程如下。
首先,构造环境空间,包括4个动态球体;其次,设计路径规划任务中的强化学习要素,根据环境与无人机的相对信息设计状态空间,依据无人机的动力学模型与扰动流体方法中的对应参数设计动作空间,结合稀疏奖励的思想设计奖励函数;最后,经动作选取时引入正态分布的TD3算法训练得到的Actor网络可以对受限制的扰动流体动态系统(Limited Interfered Fluid Dynamic System,LIFDS)算法中对应系数进行优化,该优化机制包括并行的多个TD3算法训练得到的深度神经网络,数量与当前检测到的动态障碍物数量相同。每个Actor网络的输入为无人机与障碍物的相对位置、速度、距离以及无人机自身航向角,输出为LIFDS算法中参数,结合无人机当前位置、障碍物状态信息等计算得出无人机下一时刻的位置,并形成航迹。
2 问题制定与强化学习要素
2.1 马尔可夫决策过程
无人机与环境进行交互得到动作的路径规划过程可以视作序列决策过程,可以建模成马尔可夫决策过程,再用强化学习算法进行求解。马尔可夫决策过程中当前时刻的状态与动作只与前一时刻的状态与动作有关,而与其他时刻的状态与动作无关,可表示为
M=(S,A,P,R)
(1)
式中:S为智能体感知的状态集合;A为其动作空间;P为状态转移概率矩阵;R为智能体在当前时刻执行该动作从环境中获得的奖励。
2.2 障碍环境设计
本文主要考虑三维空间下动态障碍物环境,将动态障碍物等效为动态球体,建立如下的动态障碍物的等效球体包络方程
(2)
式中:B=[x,y,z]T,表示无人机的当前位置,B0=[x0,y0,z0]T,表示障碍物的几何中心;a>0,决定了球体的半径;Γ(B)<1,Γ(B)=1,Γ(B)>1,分别表示无人机位于球体的内部,表面以及外部、从而可根据Γ(B)的取值情况判断无人机在路径规划的过程中是否发生了碰撞。
2.3 无人机动力学模型
稳定飞行的无人机运动学模型[10]如下
(3)
式中:φ和ψ分别为俯仰角与偏航角;V为无人机的飞行速度;Ix,Iy,Iz分别表示控制输入沿x,y,z轴方向上的过载;g为重力加速度。
2.4 强化学习要素
无人机路径规划任务中的强化学习要素主要包括无人机感知到的状态空间,当前的状态到下一状态执行的动作和执行当前动作所得的奖励。
2.4.1 状态空间
本文中,为了增强避开障碍物的目的感,提高收敛速度,状态空间由无人机和障碍物之间的相对关系组成,将其定义为
(4)
式中:s1表示无人机与障碍物h之间在惯性坐标系下3个坐标轴上的相对位置;s2为无人机到目标之间的相对位置;s3为障碍物的速度。
2.4.2 动作空间
基于无人机的动力学模型以及LIFDS算法,除了优化LIFDS算法中的参数ρh与σh,还需要优化一个切向系数θh。本文将动作空间定义为
A=[ρh,σh,θh]T
(5)
式中:ρh∈[1,5];σh∈[1,5];θh∈[0,π]。
2.4.3 奖励函数
奖励函数是强化学习的核心部分,极大地影响了算法的收敛性,同样决定了无人机的行为策略。本文的奖励函数设置见表1。
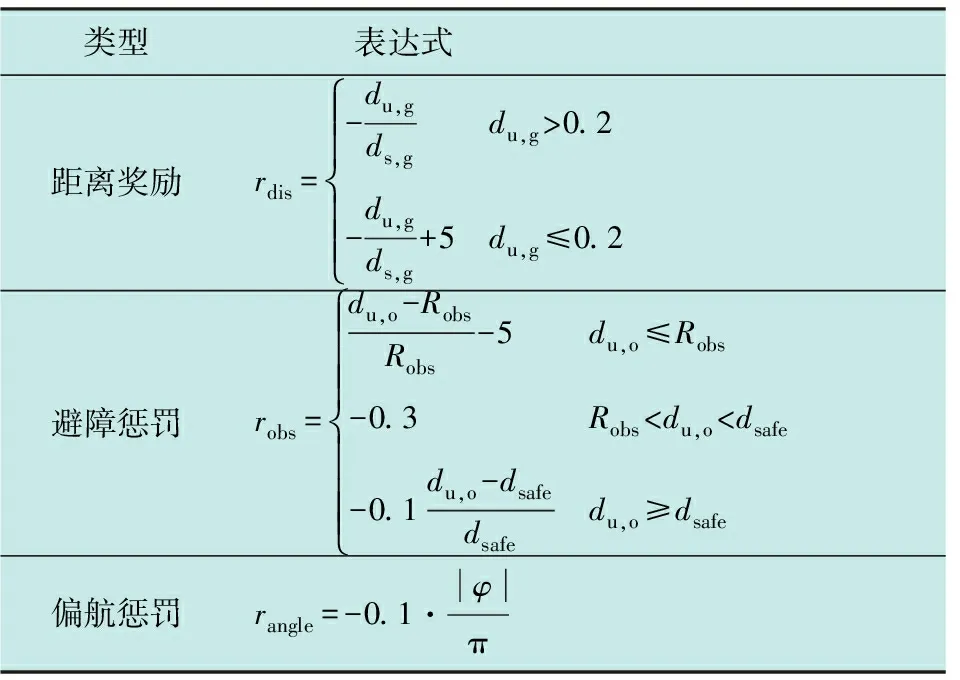
表1 奖励函数的设置
表1中:du,g为无人机到目标点的距离;ds,g为初始点到目标点的距离;du,o为无人机到障碍物的距离;Robs为球体障碍物的半径;dsafe为最小安全距离;|φ|为无人机航向与目标方向之间的夹角。
因此,无人机从环境中获取的奖励表示为
R=rdis+robs+rangle。
(6)
3 本文所提路径规划框架
3.1 受限的扰动流体动态系统算法
由于大多数算法规划出路径质量不够理想,WANG等[12]提出了IFDS算法。IFDS算法的初衷是模拟自然界的流水避石原理,即流水在无障碍时轨迹呈直线,在遇到障碍物时总能平滑地绕开障碍物,最终到达终点。该算法主要缺点是局部最小问题[11],造成此问题的主要原因是扰动矩阵的定义不全面,导致流线分布有限。因此,YAO等[11]提出了IIFDS算法,对该算法介绍如下。
矢量示意图见图2。

图2 矢量示意图
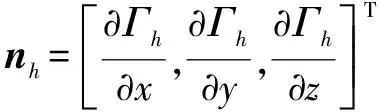
(7)
(8)
然后分别以th,1,th,2和nh为x′轴、y′轴和z′轴建立切线参考系o′-x′y′z′。因此,来自切平面的任何切向量都可以表示为
(9)
式中,θh∈[-π,π],为切向系数,是沿z′轴的旋转角度。那么在惯性参考框架o-xyz中,th可以转换为
(10)
式中,Rh为o′-x′y′z′到o-xyz的坐标变换矩阵。
定义第h个障碍物的扰动矩阵为
(11)
式中:ρh为排斥反应系数;σh为切向反应系数;Mh的第1部分即单位矩阵I为吸引矩阵,第2部分为排斥矩阵,第3部分为切向矩阵。
IIFDS的算法流程如下。
算法1 IIFDS。
以汇流体为初始流体,其速度为
更新障碍物或威胁信息:模型函数Γh,速度vh,h∈1,2,…,H。
计算加权系数
根据式(10)计算切向量。
根据式(11)计算扰动矩阵。
结束循环。
算法1中,v0为汇流体初始速度,B=[x,y,z]T,为无人机当前位置;Bt=[xt,yt,zt]T,为目标点的位置,Bk,Bk+1分别指k时刻与k+1时刻无人机的位置,ΔT为k时刻与k+1时刻的时间间隔。
可看到,IIFDS算法未对无人机的偏航角与俯仰角加以限制,将俯仰角速度的最大值设为10 rad/s,偏航角控制在[-75°,100°],即规划出无人机的俯仰角速度与偏航角度超过限制时进行截断,从而符合无人机动力学模型,将其命名为受限制的扰动流体动态系统(LIFDS)算法。
3.2 动作选取时引入正态分布TD3算法
DDPG算法因其在连续的高维动作空间中选择唯一动作的优点,可保证航迹规划的实时性,文献[10]将DDPG算法用于优化IFDS中相应的参数。本文在TD3[13]算法基础上按照正态分布进行动作选取后优化IFDS算法中相应的参数,进而实现无人机的路径规划。
TD3算法的工作流程如图3所示。
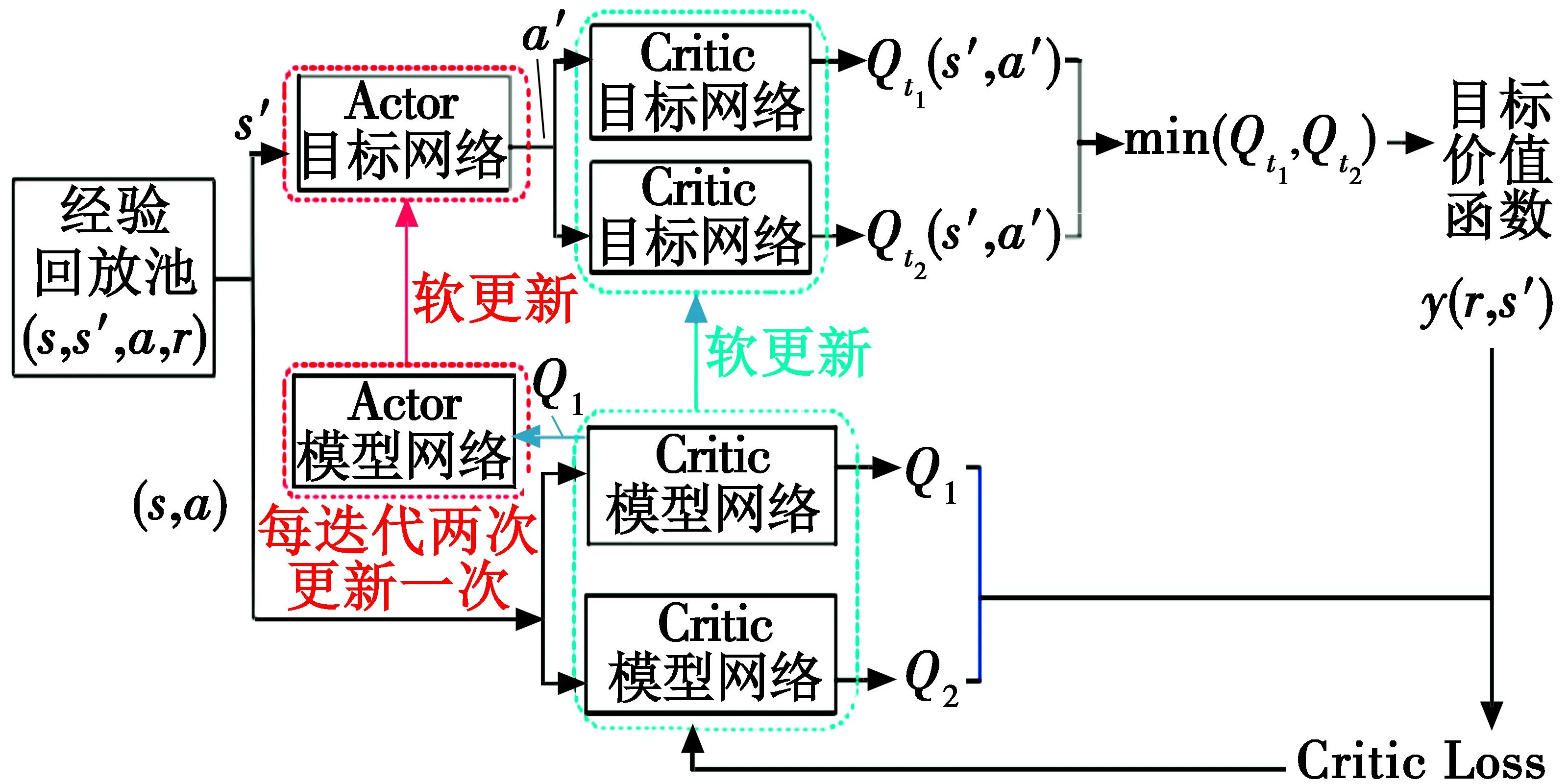
图3 TD3算法的工作流程图
作为DDPG算法的改进版本,TD3算法主要有3个改进:1) 目标策略平滑,避免DDPG算法中会因为Q值评估对某些动作-状态对产生错误尖峰而使得策略受影响,导致错误表现;2) 为了防止过高估计[7]而引入被剪切的Double-Q学习;3) 为了抑制DDPG算法中的波动,在得到值函数的准确估计后再更新策略。
从上文介绍的TD3算法中可以看出,TD3算法相对于DDPG算法的主要改进即为消除DDPG算法的错误尖峰、值函数的过高估计,同时保留了DDPG算法动作选取确定性的特点,即按照值函数最大的方向进行动作选取,这样有可能会错过一些优质的动作,因而,SAC[8]算法通过增加策略熵的技巧来增加TD3算法动作选取的随机性,受其启发,通过在TD3算法中按照正态分布进行动作来增加动作选取的随机性,引入正态分布的TD3算法的伪代码,具体如下。
算法2 动作选取时引入正态分布的TD3算法。
使用随机参数φ1,φ2,δ初始化Critic网络Q1,Q2和Actor网络Aμ
初始化经验回放池D
for episode=1 toGdo
重置环境
fort=1 toTdo
在D中存储转换元组(s,a,r,s′)
从D中抽样一批E=(s,a,r,s′)
计算目标动作
计算目标Q值y(r,s′)
使用如下梯度下降一步更新Q函数
ifjmodpolicy_delay= 0 then
使用如下梯度上升一步更新策略
更新目标网络
end if
end for
end for。
3.3 网络结构
上文介绍的Actor网络与Critic网络所采用的网络结构设计如图4所示。

图4 TD3算法的网络结构
Actor网络由输入层、全连接的神经网络层(FC)、修正线性单元(ReLU)激活函数层、双曲正切(tanh)激活函数层构成;Critic网络将状态-动作对作为其输入,并生成状态动作值函数,即Q值,由输入层、全连接的神经网络层(FC)、修正线性单元(ReLU)激活函数层和双曲正切(tanh)激活函数层构成。
3.4 本文算法的总体流程
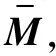
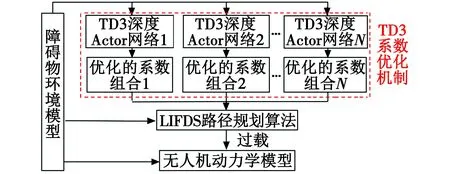
图5 本文算法总体流程图
4 仿真与分析
4.1 实验平台设置
图6所示为仿真的6种环境。
图6中,每个环境中存在4种运动方式的动态球体,黑色轨迹为动态球体的轨迹,蓝色轨迹为所提算法规划出的无人机运动轨迹,为了验证本文算法的泛化性,在环境Ⅱ,Ⅳ与Ⅵ中加入一个随机运动的球体。球体半径为0.8 m,无人机从绿色的起始点飞向红色的目标点,偏航角速度最大值限制为10 rad/s,最大俯仰角速度限制为10 rad/s,偏航角范围限制为[-75°,100°]。
在本文算法中,最大回合数为3000,最大步数为500。Adam Optimizer[14]用于学习网络参数,Actor和Critic网络学习率都设置为0.001。此外,折扣因子γ=0.99,软更新率τ=0.005,经验回放池为106,min-batch为128,探索噪声中σ=0,剪切噪声限制c=0.5,延迟步数为2。
4.2 本文所提算法的性能
图7所示为无人机LIFDS与DDPG算法、原始TD3算法、SAC算法融合与本文算法在6种测试环境中所获得的平均回合奖励。
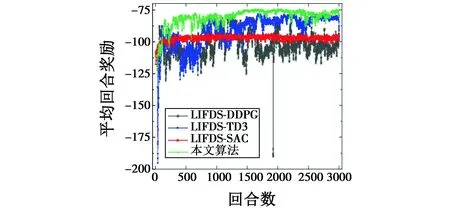
图7 平均回合奖励
由图7可以看出:本文算法在500回合左右基本实现了奖励函数的收敛,而原始的TD3算法在1500回合后才基本实现收敛;虽然SAC算法收敛速度很快,但收敛的奖励值比本文算法低;DDPG算法虽有收敛的趋势,但会出现剧烈的振荡。因而验证了对TD3算法的改进提升了算法的性能。
表2所示为6种测试环境中1000回合后平均回合奖励、路径的描述性统计结果。

表2 描述性统计
由表2可以看出,虽然LIFDS与SAC算法结合的算法标准差最小,但其平均奖励比其他算法都低,而本文算法的平均奖励值高于所有对比算法,且标准差仅有2.932,验证了本文算法在训练稳定性方面与平均奖励值方面达到了平衡。另外,将训练过程中最好的模型用于路径规划,表2展示了6种测试环境中的平均路径长度以及飞行过程中最大飞行方向变化(LS)的平均值,可以看出,到本文算法在路径平滑度方面都优于对比算法,验证了所提算法相对其他算法在动态障碍物环境下无人机路径规划任务的有效性。
4.3 奖励函数的效果
为验证所设计的奖励函数有效性,本文增加关于奖励函数的消融实验,3种不同的奖励函数设计如下:1) 本文算法的奖励函数,已在3.3节详细阐述,命名为“our algorithm”;2) 去掉“偏航惩罚”,命名为“wo off-route”;3) 去掉“安全屏障”,即当Robs 图8 不同奖励函数的平均回合奖励 由图8可以看出,与其他奖励函数相比,本文的奖励函数在训练神经网络时可以加快收敛速度,并且更稳定,说明所设计的奖励函数中的部分对引导智能体完成路径规划的任务都是有效的。 针对动态障碍环境,提出了一种基于扰动流体与TD3算法的无人机路径规划框架,使得无人机在实时避障与规划路径的同时,能够尽量满足路径的平滑性。为了增强TD3算法对环境的探索,在TD3算法中按照正态分布选取动作。为了增大测试环境的复杂度,从而验证本文所提算法的泛化性,在起点与终点中间添加了随机运动的球体,仿真结果验证了所提算法相对传统算法以及对比算法在路径平滑度、长度以及网络训练的收敛速度、稳定性方面的优势,并通过对所提奖励函数的消融实验验证其对提升训练速度以及稳定性方面的优势。关于进一步的研究,尝试在Gazebo[15]环境中进行更接近真实环境的仿真以及可视化。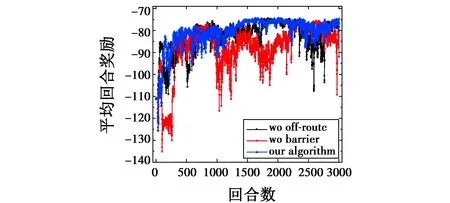
5 结论
