一种新型趋近律的PMSM 模糊自适应终端滑模控制*
2024-01-15冯琪茗董秀成
冯琪茗 董秀成, 刘 元
(1.西华大学电气与电子信息学院 成都 610039;2.四川大学锦江学院电气与电子信息工程学院 眉山 620860)
1 引言
永磁同步电机(Permanent magnet synchronous motor,PMSM)由于效率高、转矩能力大、构造简易、功率密度高等优点,通常用于高性能应用中[1]。因此,为了在设计过程和实施中提高效率,需要对PMSM 进行速度控制。在电机控制领域中,PI 控制器一直因其结构简单、调节方便而备受青睐,但是,传统PI 控制器仍然存在大量的问题,在现实控制中,大多数系统都是非线性系统,而PI 控制器属于线性控制器,用线性控制非线性,会导致精度降低。而且在实际控制中,传统PI 控制器无法应对系统参数变化带来的问题。在高精度控制场景下,PI 控制器已经无法胜任[2]。
随着现代控制理论的发展,为解决传统PI 控制器的不足,大量学者开始结合现代控制理论研究新的控制器,如神经网络控制、预测控制、模糊控制、滑模控制(Sliding mode control,SMC)等[3-6];从首次提出到现在,经过长期的发展,SMC 一直是控制领域无法绕开的话题。SMC 也被称为变结构控制,因其对系统自身参数变化和外部扰动不敏感,具有响应快速、鲁棒性强和容易实现的优点,广泛应用于PMSM 控制系统中,而且其控制的优越性也得到了证实[7]。但是传统SMC 仍然存在问题,一是在满足稳定性条件下,必须使滑模切换增益大于系统不确定项的上界,这样会造成SMC 产生严重的抖动[8]。二是由于传统SMC 采取的滑模面是线性的,所以会存在收敛速度慢的问题,只有在时间趋于无穷时,误差才会收敛到零[9-10]。
在解决传统SMC 问题的研究过程中,国内外学术专家付诸了很多的努力,也取得了诸多的研究成果。针对滑模抖振问题,研究发现是由于系统状态轨迹在滑模面上做高频切换运动而产生的,为了抑制因抖振产生的影响,文献[11]提出了一种基于新型变速趋近律的滑模控制器,选取变带宽的趋近方式,能够很好地抑制稳态转矩脉动。文献[12]提出采用可变边界层的饱和函数取代传统的符号函数来抑制抖振,虽然抖振在一定程度上能够得到抑制,但系统的响应速度比较慢。文献[13]提出采用分数阶终端滑模控制,并设计基于半正定屏障函数的自适应控制,对不确定扰动的上界进行估计来削弱不确定性因素对系统的影响,可以保证跟踪误差在有限时间得到收敛,避免过高的控制增益估计且削弱了系统抖振。文献[14]提出一种新型的模糊滑模速度控制器,通过系统状态量到达滑模面的距离和滑模增益来设定模糊规则,使得滑模趋近速度可以进行动态调整,然后选取连续的sigmoid 函数取代不连续的符号函数,让系统可以进行平滑切换,提高了控制系统的响应速度并且增强了控制系统的抗干扰能力。
目前,无传感器策略是一种可测量变量技术,对消除布线和降低信号噪声起到了较大的作用[15-16]。国内外的学者们在对无传感器控制技术的研究过程中,也取得了诸多的研究成果。例如,文献[17]提出一种新型指数型函数,该方法可以降低滑模函数带来的抖振。文献[18]提出一种新型方波注入法,该方法可以降低高频电压矢量信号畸变,提高观测器估计角度的精度。文献[19]提出了改进型滑模观测器,该观测器在抑制抖振的同时,也能提高算法的估计精度。
本文在模糊滑模控制的基础上,提出了一种改进的算法。一是在全局快速终端滑模控制的基础上,根据文献[20]所提趋近律,设计了一种新的复合趋近律,很大程度上提高了系统的收敛速度,为抑制抖振问题,采用将饱和函数放入幂次项中,实现了和幂次趋近律相同的性质,抖振也能得到很好的抑制。二是根据线性化反馈技术,以误差函数导数的绝对值为补偿构建了自适应干扰估计项,并将估计结果作为补偿传递到速度控制器,避免开关增益的使用,试验仿真表明,本文所设计速度控制器能使电机转动抖振得到有效削弱,电机控制系统的动态响应能力和稳定性得到提高。
2 PMSM 数学模型
三相永磁同步电机是一种非线性、强耦合的多变量系统,并且结构较为复杂,为了便于分析,常常将三相PMSM 看为理想型电机,同时满足理想条件。为了方便控制器的设计,需要选取合适的坐标变换对三相PMSM 的数学模型进行解耦和降阶变换,本文采取同步旋转坐标系对其进行解耦与降阶,故PMSM 的数学模型在d-q旋转坐标系下可以表示为
式中,ud与uq分别表示对应的d轴、q轴电压,id与iq分别表示对应的d轴、q轴电流,ωm表示机械角速度,ψf表示永磁体磁链,pn表示极对数,Rs表示定子电阻,Ls表示定子电感,J表示转动惯量,TL表示负载转矩。
3 新型复合趋近律的设计与分析
3.1 传统滑模趋近律
一般来说,传统滑模控制器的设计主要有两个部分,一是滑模面的选取,二是趋近律的选择,前者保证系统误差的收敛,而后者则保证滑模趋近运动的动态品质。传统滑模趋近律通常选择高为炳院士提出的指数趋近律,如下所示
式中,ε、q为任意正实数,sgn(⋅)代表符号函数。
假设系统状态在t时刻到达滑模面,对式(2)在0 到t进行积分可得到达时间t为
式中,s(0) 为t=0 时刻滑模面的初始位置。
由式(3)可知,若要减小到达滑模面的时间,则需要增大ε,但过大的ε值又会使系统产生剧烈的抖振现象,使系统的抗干扰能力降低。
3.2 新型复合趋近律
基于上述指数趋近律的缺点,本文提出了一种新型复合趋近律
式中,a>0 ,0<α<1 ,0
相比于符号函数,采用饱和函数可以保证在边界层里面使用线性控制,在边界层外面使用切换控制,从而可以抑制由于滑模面切换运动所带来的抖动。
由式(4)可知,新型复合趋近律由三部分构成,当系统状态远离滑模面时, -a|s|αsat(|s|-1)s起主要作用,即当|s|> 1时,趋近律约等于 -a|s|αs,故状态变量能很快地收敛到滑模面,从而保证系统有更短的到达时间,增强了系统的动态响应性能。而当系统状态趋近滑模面时,f(x,s) ≈kg(|x|),故趋近律约等于kg(|x|),在控制律的作用下,|x|将会逐渐趋近于零,所以趋近速度也会逐渐趋近于零,能有效解决因固定增益带来的抖振问题。
为验证所提趋近率的效果,在Simulink 中进行仿真,不同趋近率下滑模函数的收敛过程如图1 所示。
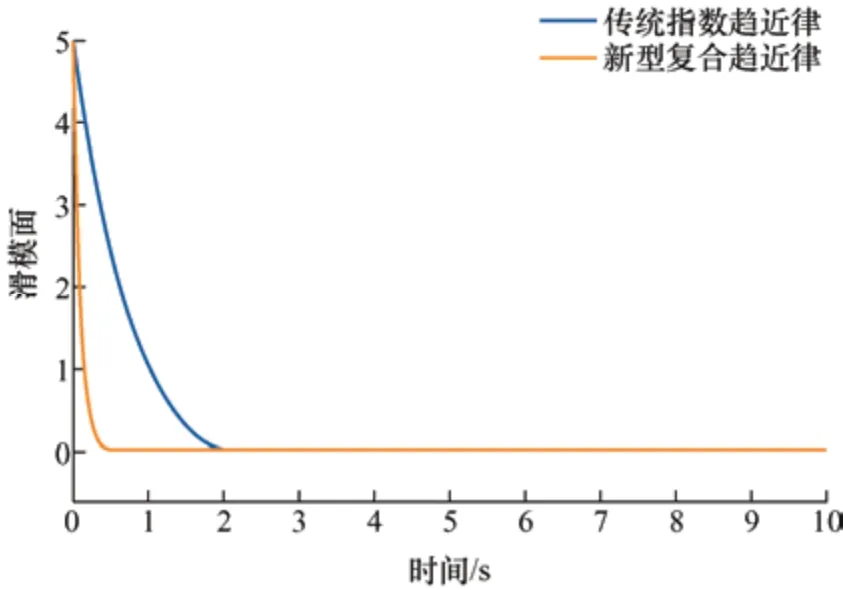
图1 不同趋近律下s 变化曲线
由图1 可知,与传统指数趋近律相比,新型复合趋近律的趋近速度和响应速度有明显的提升。
4 自适应全局快速终端模糊滑模控制器的设计与分析
4.1 传统滑模控制器
定义电机系统的状态变量为
式中,reω表示电机的参考转速,mω表示电机的实际转速。
根据式(1)和式(6)可知
传统滑模控制一般选取滑模面为
式中,c> 0。
选取指数趋近率使PMSM 驱动系统具有较好的动态品质,故控制器的表达式为
式中,ε、q>0。
q轴参考电流可由传统的滑模控制器获得
由滑模到达条件ss˙<0,可以很容易验证在式(11)的作用下,控制系统是渐进稳定的。
4.2 全局快速终端滑模控制器
由于传统滑模控制器通常使用线性超平面,误差无法快速收敛至零界点。基于线性滑模表面和快速终端吸引子设计全局快速终端滑模控制器,以保证控制系统在有限时间内从任意初始状态迅速达到平衡状态。
定义全局快速终端滑模面函数为
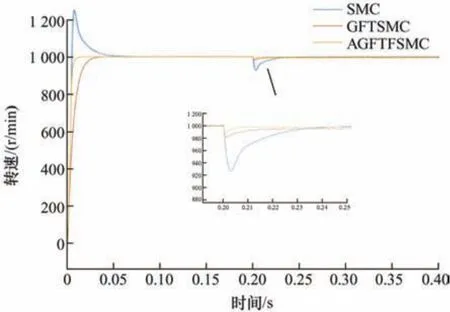
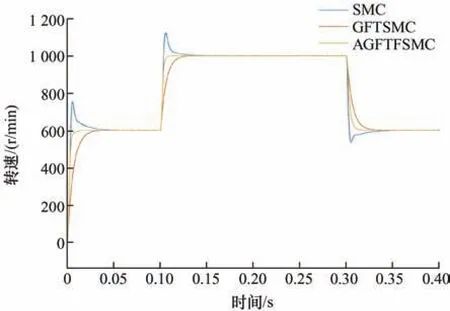
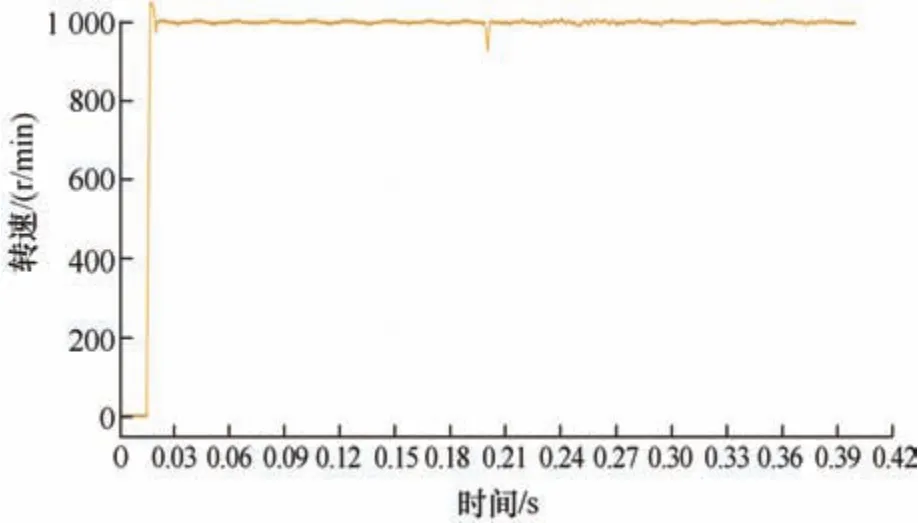
式中,α> 0,β> 0,为正奇数且q 在系统状态趋近于平衡点的情况下,收敛时间的确定由x˙ =-αx占主导地位;在系统状态离开平衡点的情况下,收敛时间由占主导地位,故有 联立式(7)、式(12)和式(13)可得全局快速终端滑模控制器(Global fast terminal sliding mode controller,GFTSMC)的表达式为 GFTSMC 采取转速误差为状态变量构建滑模面,当转速误差沿滑模面运动到平衡点时,可以得到q轴参考电流。 加入新型复合趋近率得到速度控制器表达式为 构建李雅普诺夫函数 故有 根据李亚普洛夫稳定性定理,全局快速终端滑模控制器是稳定的。 由于在电机运转过程中,伴随着不确定项,除了外部负载带来的扰动之外,还有自身内部参数的变化带来的扰动,为了便于分析,用d(t)来表示包含负载转矩TL的一切扰动,即 式中,d(t)是有界的,且具有某一上界k(t),使d(t) ≤k(t)。 考虑扰动之后,根据式(15)设计滑模控制器为 由式(19)可知,将扰动当作已知量反馈到控制率中,当出现外部扰动时,控制器可以及时响应扰动的变化。 由于扰动d(t)时变不确定,为保证系统的稳定性,当d(t)较大时,扰动上界k(t)也要足够大,但过大的上界会造成系统的抖振,针对这一问题,将采用模糊理论的模糊推理来解决。 为消除系统抖振,k(t)应随着扰动d(t)的变化而变化,且k(t)必须时刻大于扰动d(t)。为保证估计扰动处处大于实际扰动,设计一种自适应扰动估计办法,首先采用李亚普诺夫函数的导数作为系统的输入,系统的输出为 Δk(t),其次采用模糊系统将切换项导数的绝对值作为优化项,进而使得出的估计值更加接近真实的扰动值,减小系统抖振。 设基础的模糊系统由IF-THEN 形式的模糊规则构成 R(j):IFx1isA1jand ··· andxnisA1jTHENyisBj。 选取乘积推理机、单值模糊器和中心平均解模糊器,则模糊系统的输出为 引入模糊向量ξ(x),式(20)变为 式中,θ=(y1,…,ym)T,ξ(x) = (ξ1(x) , … ,ξm(x))T。 根据线性化反馈技术,并且采用模糊系统逼近,本文使用积分的方法对k(t)进行估计,则 在估计值的基础上加一个很小的常数η(η> 0)得到扰动估计值,确保处稍大于实际扰动d(t),如下所示 根据模糊逼近理论,自适应模糊系统可以实现使逼近误差非常小。因此≤ 0。 基于模糊理论设计如下系统。 根据模糊规则,以V˙为输入,Δk为输出,模糊集设置如下 式中,NB、NM、NS、ZO、PS、PM、PB 分别对应的是负大、负中、负小、零、正小、正中、正大,隶属度函数图像如图2 所示。 图2 隶属度函数 为了使估计值更靠近真实值,设计如下的模糊规则,如表1 所示。为了使PMSM 系统迅速调节到稳定状态,应该快速增大,也就意味着Δk迅速增大,故当为PM 和PB 时,Δk为PB。而当为PS 时,Δk可保持不变。相应地,为使抖振得到快速削弱,Δk应迅速减小,故当为NM 和NB 时,Δk为NB。同理,当为其他值时,Δk可保持跟随。 表1 永磁同步电机参数 综上所述,自适应全局快速终端模糊滑模控制器(Adaptive global fast terminal fuzzy sliding mode controller,AGFTFSMC)结构图如图3 所示。 图3 控制器结构框图 由于传统滑模观测器观测的反电动势带有不连续的高频信号,这些高频信号的滤除过程会影响观测精度[21],故本文采用超螺旋滑模观测器代替传统滑模观测器。 超螺旋算法的数学表达式如下 式中,k1、k2表示滑模增益,ρ1(x1,t)、ρ2(x2,t)表示外部扰动项。式(27)中扰动项满足 式中,σ1表示任意正常数,式(27)中的增益满足 式(27)所述系统中,由于原点是一个平衡点,所以该点在全局上具有逐渐趋近稳定的特性,故系统经过一段时间后,其状态变量的值将会趋向于零,并最终稳定在原点处。系统状态的稳定性可以通过控制系统的设计和参数调整来实现。 超螺旋滑模观测器设计如下所示 当超螺旋滑模观测器的估计误差到达滑模面时,可以得出估计值约等于真实值,即=0,故可以根据滑模控制的等效原理得到反电动势值,即 本文采用反正切函数来获得转子位置。永磁同步电机整体控制框图如图4 所示。 图4 系统控制框图 在Matlab/Simulink 中进行仿真研究,以验证本文所提改进算法的有效性,下面对SMC、GFTSMC、AGFTFSMC 三种控制方式进行仿真对比试验,仿真中均采用超螺旋滑模观测器来获得转速和转子位置信息。 试验仿真中采用固定步长ode3 算法,且固定步长时间设定为2×10-7s,仿真时间设定为1 s,永磁同步电机参数如表2 所示。 表2 永磁同步电机参数 (1) 工况一(空载工况)。仿真过程中,在电机空载起动后转速从0 升至1 000 r/min,图5、图6 对比了三种控制方式的性能,可以看出采用SMC 控制方式虽然响应速度较快,但出现了明显的超调,而且调节时间较长,采用全局快速终端滑模控制器虽然可以很好地抑制超调,但响应速度却降低了,而本文所提方法不仅能抑制超调,而且相比传统控制方法,响应速度也得到了提高,电磁转矩脉动也得到了抑制。 图5 三种方法转速曲线对比 图6 三种方法电磁转矩曲线对比 (2) 工况二(负载工况)。仿真过程中,在电机空载起动后转速从0 升至1 000 r/min,并且在0.2 s时负载转矩从0 突增至5 N ⋅ m。三种控制方式的性能对比如图7、图8 所示,可以看出,在突加负载后,传统SMC 方法转速波动最为明显,转速下降了73 r/min,而且再次到达给定转速时间较长,采用GFTSMC 方法转速波动次之,下降了18 r/min,再次达到稳定转速时间明显提高,相比之下,本文所提AGFTFSMC 方法转速波动明显减小,且再次回到给定转速时间进一步缩短,达到稳定控制的效果,抗扰性能更优。 图7 三种方法转速曲线对比 (3) 工况三(变转速工况)。仿真过程中,在电机空载起动后转速从0 升至600 r/min,在0.1 s 时转速升至1 000 r/min ,在0.3 s 时转速再次降至600 r/min。三种控制方式的性能对比如图9、图10所示,可以看出,在变转速状况下,采用传统SMC控制器依然存在较大的超调,抗扰性能明显不足,GFTSMC 方法响应速度最慢,响应性能不足,抗干扰能力稍差,而本文所提AGFTFSMC 方法响应依然更快且没有超调,能很好地适应各种工况,抗干扰性能优。通过仿真最终验证了本文所提方法具有更优的动态性能。 图9 三种方法转速曲线对比 图10 三种方法电磁转矩曲线对比 为了验证所提自适应模糊滑模控制器的可靠性,搭建永磁同步电机控制试验平台,如图11 所示。该试验平台以TI公司TMS320F28335数字芯片为控制芯片,试验系统为模块化设计,共有三个主要部件组成,分别为DSP 核心模块、IPM 功率模块、电机试验平台。 图11 试验平台 基于试验平台对所提AGFTFSMC 方法进行验证,试验过程中,电机从零速开始起动到1 000 r/min,运转过程中,在0.2 s 加入负载,变转速工况,试验结果如图12~15 所示。 图12 SMC 突加负载转速变化 从图12 和图13 可以看出,突加负载后,采取AGFTFSMC 方法电机转速在轻微波动后,能够很快回到给定转速,而SMC 波动较为明显;由图14 和图15 可以看出,AGFTFSMC 方法可以快速响应转速变化,与仿真结果基本一致,进一步验证了所提方法的准确性与可靠性。 图13 AGFTFSMC 突加负载转速变化 图14 SMC 变转速曲线 图15 AGFTFSMC 变转速曲线 本文在全局快速终端滑模控制的基础上,设计改进型复合趋近律,结合模糊滑模控制,提出新型滑模控制器。并结合超螺旋滑模观测器进行了仿真试验,结论如下所述。 (1) 所提新型复合趋近律可以大幅缩短到达滑模面的趋近时间,并有效抑制滑模抖动,提高系统动态响应速度。 (2) 以函数导数绝对值构建的自适应扰动估计项,将扰动估计值反馈补偿到控制器中,加强了系统的抗扰能力。 (3) 试验结果表明,AGFTFSMC 能应对各种工况,在抑制系统抖动的同时,转速没有出现超调,提高了系统的响应速度,改善了观测器的跟踪效果,超螺旋滑模观测器的观测精度得到提高,系统的抗扰动性能也得到加强,具有更优的动态性能。4.3 稳定性证明
4.4 自适应扰动估计
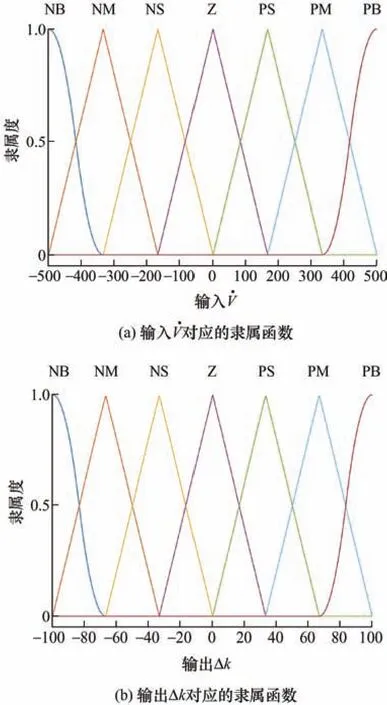
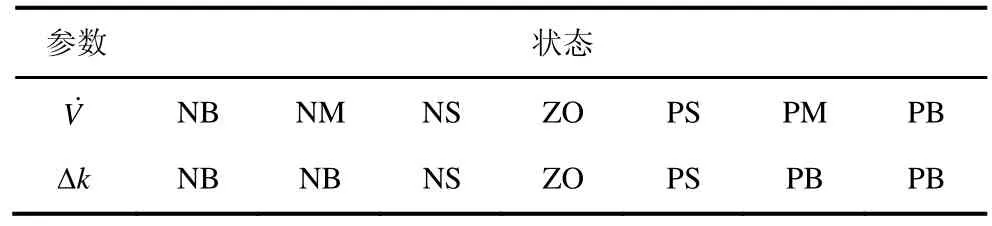

5 超螺旋滑模观测器的设计
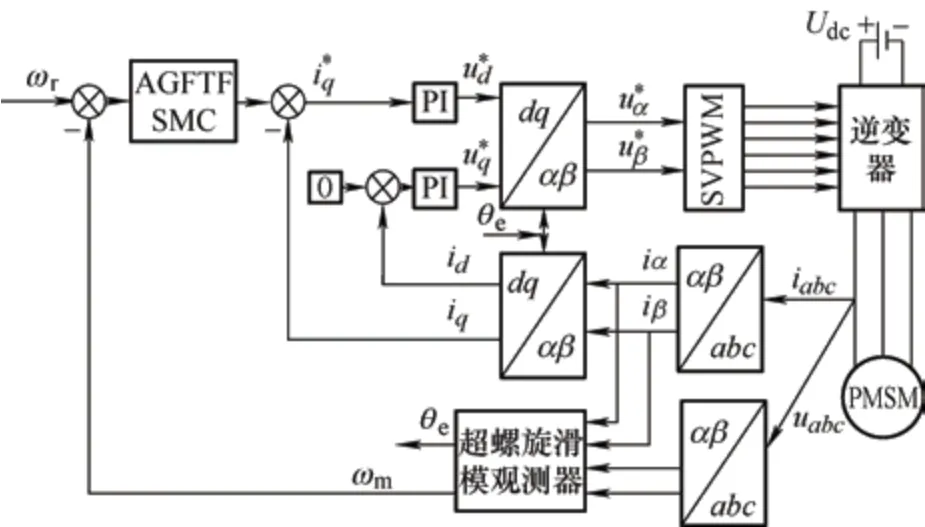
6 试验仿真及结果分析
6.1 仿真验证



6.2 试验验证




7 结论
