永磁游标电机转矩特性研究*

林宝全 李 捷 杨公德

(1.福州大学电气工程与自动化学院 福州 350108；2.福州大学福建省新能源发电与电能变换重点实验室 福州 350108)

1 引言

永磁游标电机具有转矩密度高、结构简单、效率高等优点，广泛应用于电动船舶、风力发电和机器人伺服等低速大转矩驱动系统[1-4]。永磁游标电机的定转子具有不同的极对数，定转子间无直接耦合关系。基于气隙磁场调制效应，永磁游标电机可实现永磁磁场和电枢反应磁场的间接耦合，并产生稳定电磁转矩[5-8]。相比于传统永磁同步电机，永磁游标电机的转矩密度得到大幅度提高。

随着气隙磁场调制理论的提出，永磁游标电机的工作原理得到了广泛研究[9-11]。文献[12]提出一种精确子域解析模型，考虑了定子开槽效应和调制齿对气隙磁场的影响，计算得到永磁游标电机的气隙磁场谐波分布，并采用有限元法验证了解析模型的正确性。文献[13-14]对比研究了具有相同机械结构的永磁游标电机和传统永磁同步电机，并分析了永磁游标电机转矩脉动较小、反电动势正弦度较高的原因。

目前，针对永磁游标电机转矩特性的研究主要集中在拓扑结构创新，如分裂极永磁游标电机、复合结构[15-16]等，文献[17]提出了一种交替极永磁游标电机，该电机在双向气隙磁场调制效应作用下，能有效提高气隙磁场谐波含量，具有更高的转矩密度。文献[18]提出了一种切向励磁游标电机，虽然辐条型永磁体结构能产生聚磁效应，但该结构应用于永磁游标电机中，将产生磁障效应，削弱电机转矩密度。现有文献分析了定转子结构对永磁游标电机转矩性能的影响[19-20]，但其本质是永磁游标电机的磁动势和磁导分布不同，气隙磁场有效工作谐波存在差异，导致不同定转子结构下永磁游标电机的转矩性能变化较大。因此，永磁游标电机关键结构参数对气隙磁场调制效应和电机转矩性能的影响仍需得到进一步研究。

基于气隙磁场调制理论，以一台三相12 槽/20极永磁游标电机为研究对象，探索永磁游标电机的转矩产生机理。为提升永磁游标电机的转矩性能，采用基于响应面模型的遗传算法对电机关键结构参数进行多目标优化。利用麦克斯韦应力张量法定量分析气隙磁密谐波对电磁转矩的贡献。通过分析不同结构参数下永磁游标电机气隙磁密谐波，研究关键结构参数对电机气隙磁场调制效应的影响。

2 永磁游标电机工作原理分析

2.1 永磁游标电机结构

图1 为三相12 槽/20 极永磁游标电机(PMVM)的结构示意图，N 极和S 极永磁体交替排列放置于转子铁心表面上，定子采用半开口槽结构。PMVM的基本结构参数如表1 所示。

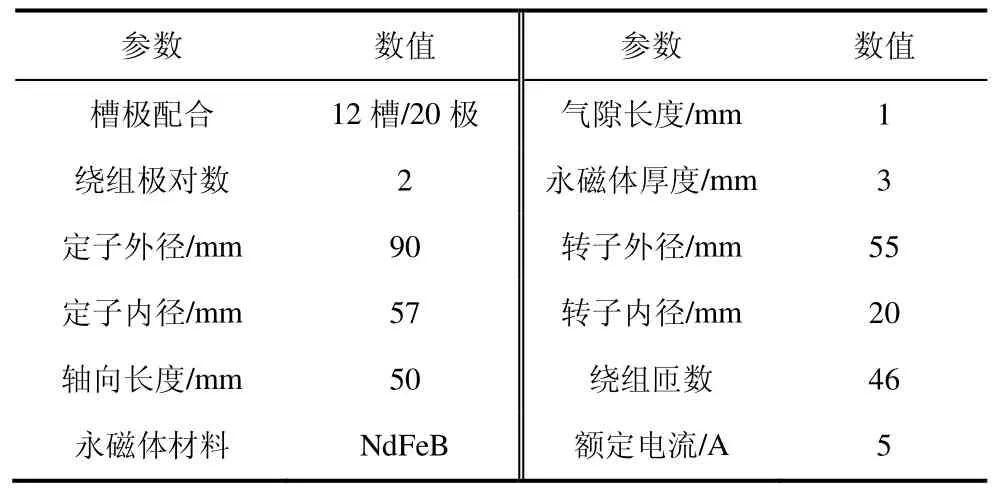
表1 PMVM 基本结构参数

图1 PMVM 结构示意图

2.2 气隙磁场调制原理分析

PMVM 定子的齿槽结构起到调制器的作用，定子齿槽的交替排布引起定子磁导变化，导致PMVM在气隙中调制产生大量磁场谐波，在极对数相等且转速相同的磁场谐波的相互作用下，PMVM 产生稳定电磁转矩。

以定子齿的中心线作为永磁磁动势的参考轴，建立相对极坐标系，永磁磁动势可以表示为

式中，FPMi为永磁磁动势第i次谐波幅值，ωr为永磁转子机械角速度，θ为气隙周向位置，0θ为永磁转子的初始位置。

忽略漏磁和定转子铁心局部磁饱和，由定子齿槽结构引起的定子磁导调制函数可表示为

式中，Λs0为定子磁导直流分量幅值，Λsm为定子磁导m次谐波幅值。

永磁气隙磁场可表示为永磁磁动势和定子磁导调制函数的乘积，表达式为

由式(3)可知，定子磁导直流分量不改变永磁磁动势的谐波次数和谐波旋转速度。因此，仅由永磁体产生的永磁气隙磁场中存在iPr次谐波分量，谐波旋转速度为ωr；在定子磁导谐波的调制作用下，永磁体产生的永磁气隙磁场谐波次数为|iPr±mNs|，谐波旋转速度为iPrωr/(iPr±mNs)。

PMVM 三相电枢绕组在空间上互错π/6，则单相电枢反应磁动势为

式中，Fj为单相电枢反应磁动势第j次谐波幅值，ωe为电角速度，φ0为电枢电流初相位。

由式(2)和式(4)可求得电枢反应气隙磁场为

由式(5)可知，由电枢绕组产生的电枢反应磁动势在定子磁导的调制作用下，产生一系列谐波分量，谐波次数包括jPa和|jPa±mNs|，对应的谐波旋转速度分别为ωe/jPa和ωe/(jPa±mNs)。

在PMVM 电磁转矩的产生过程中，永磁气隙磁场谐波可以与次数相等、转速相同的电枢反应气隙磁场相互耦合，产生稳定电磁转矩；而当永磁气隙磁场谐波与相同次数的电枢反应气隙磁场谐波具有不同旋转速度时，将产生转矩脉动。为获得最大输出转矩，PMVM 电枢绕组极对数、定子槽数和转子永磁体极对数遵循如下设计原则

式中，Pr为转子永磁体极对数，Ns为定子槽数，Pa为电枢绕组极对数。

3 电磁转矩性能优化设计

为保证PMVM 低速大转矩工况需求，选取电磁转矩作为PMVM 转矩性能优化目标。此外，转矩脉动是衡量电机负载运行时转矩波动情况的重要性能指标，而齿槽转矩则会引起电机空载运行时的振动和噪声。虽然齿槽转矩是引起转矩脉动的重要因素，但非正弦畸变的反电动势和气隙磁场谐波分量同样会导致电机的转矩脉动，并且二者所反映的电机转矩品质也并不相同。因此，针对PMVM 转矩性能的优化设计，有必要同时考虑转矩脉动和齿槽转矩。以提高平均电磁转矩Te、减小转矩脉动Tr和降低齿槽转矩Tcog作为优化目标，PMVM 电机结构参数标注如图2 所示。

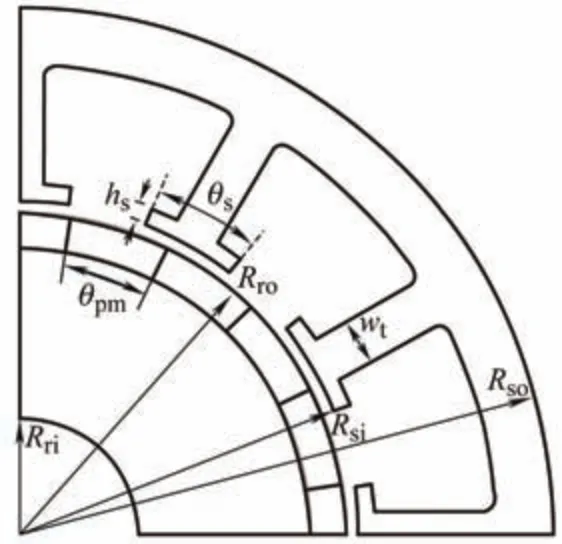
图2 PMVM 结构示意图

基于气隙磁场调制效应，PMVM 能够实现低速大转矩的输出特性。永磁体排列方式决定了永磁磁动势的分布，定子齿槽结构决定了定子磁导调制函数。因此，选取永磁体极弧系数θpm、定子齿宽wt、齿靴厚度hs和定子极弧系数θs作为PMVM 电磁转矩性能优化的结构参数。

为准确分析结构参数对PMVM 电磁转矩性能的影响，并根据影响程度确定合理的结构参数，利用有限元对电机性能进行初步分析，引入敏感度系数衡量结构参数对各优化目标的敏感程度，其中敏感度系数Si可定义为

式中，xi为结构参数；f(xi)为优化目标；E(f(xi)/xi)为结构参数xi取不同数值时，优化目标f(xi)的平均值；V(E(f(xi)/xi))和V(f(xi))分别表示E(f(xi)/xi)和f(xi)的方差，敏感度系数Si越高，表示xi的变化对f(xi)的影响程度越大。

根据图3 所示结构参数的敏感度分析结果，定子齿槽结构参数对PMVM 电磁转矩、转矩脉动、齿槽转矩均具有较大影响，确定结构参数的取值范围如表2 所示。

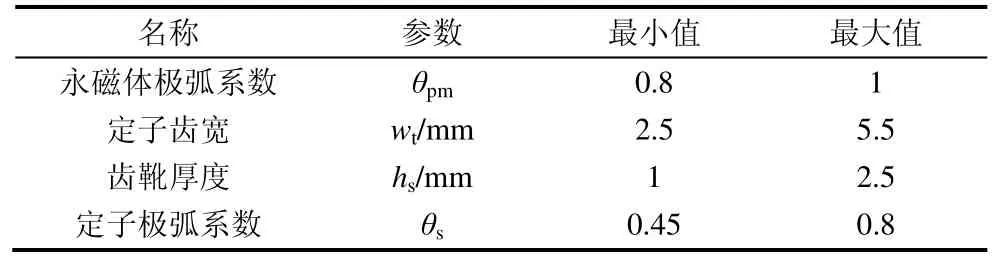
表2 PMVM 结构参数取值范围

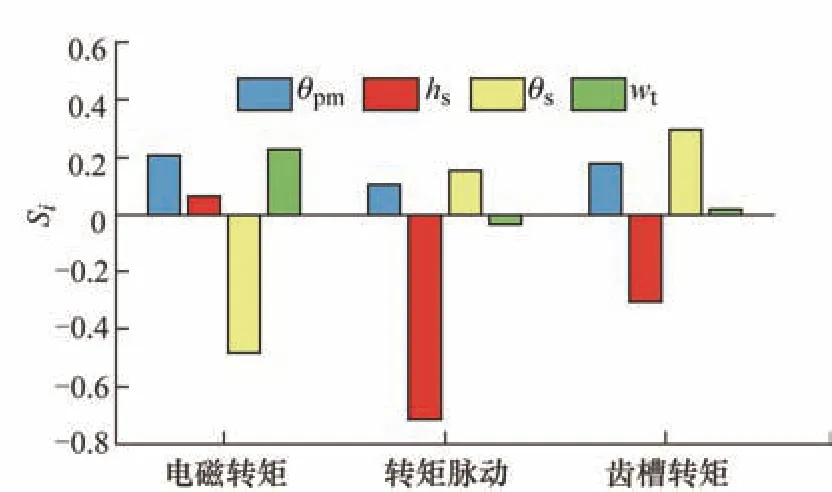
图3 敏感度分析结果

根据PMVM 结构参数的变化范围，建立中心复合试验设计(Central composite design, CCD)试验矩阵，并采用有限元法对指定试验设计点进行求解，得到响应面函数模型如 图4 所示。

由图4a 可知，随着θs减少，定子槽口减小，PMVM 电磁转矩明显增大。对比图4b 和图4c 可知，θpm、hs对转矩脉动和齿槽转矩的影响近似相同。转矩脉动和齿槽转矩均随着θpm的增大而逐渐增大。当hs增大时，转矩脉动和齿槽转矩减少。而当θs减小时，转矩脉动和齿槽转矩先增大后减小。各个响应面模型均存在极值，结构参数同样存在最佳取值范围，但在不同响应面模型中结构参数的最佳取值范围不同。因此，为平衡不同优化目标间的相互影响，采用带精英策略的非支配排序遗传算法(NSGA-Ⅱ)进行多目标优化，设置初始样本数为4 000，每次迭代样本数为800，经9 次迭代计算后，得到帕累托(Pareto)解集及最优点，如图5 所示。

为验证多目标优化效果，对比分析PMVM 优化前后的转矩性能，优化前后的PMVM 结构参数如表3 所示。图6 给出了空载和负载两种工况下PMVM 转矩性能优化前后的比较结果。由图6a 可见，通过对永磁体和定子齿槽结构参数进行优化，周期性变化的齿槽转矩受到明显抑制，PMVM 齿槽转矩由优化前的峰峰值0.291 N·m 降低到优化后的峰峰值0.066 N·m，减少了77.3%。PMVM 电磁转矩如图6b 所示，优化后的PMVM 平均转矩提高了0.7%，而转矩脉动由优化前的13.4%降低到优化后的2.5%。

表3 PMVM 结构参数初始值与优化值

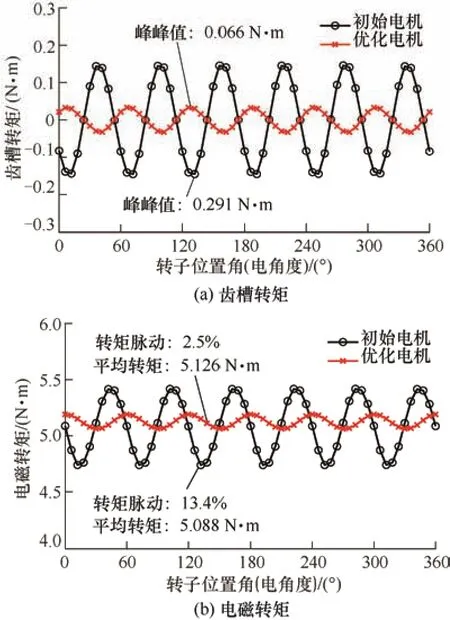
图6 优化前后的PMVM 转矩性能

4 转矩量化分析

采用麦克斯韦应力张量法建立气隙磁密谐波分量与电磁转矩的对应关系，PMVM 电磁转矩可表示为

式中，rg为气隙半径；μ0为真空磁导率；la为电机轴向长度；Br(θ,t)和Bt(θ,t)分别为电机负载时气隙磁密的径向和切向分量，可分别表示为

式中，Brk和θrk分别为径向气隙磁密k次谐波的幅值和相位；Btk和θtk则分别为切向气隙磁密k次谐波的幅值和相位。

根据式(9)中的径向和切向气隙磁密谐波计算得到瞬态电磁转矩为

根据式(10)可知，次数相等的径向和切向气隙磁密谐波存在一定相位差时，可产生稳定电磁转矩。由于幅值较小的气隙磁密高阶谐波所贡献的电磁转矩较小，忽略其所产生的电磁转矩。

分别对负载工况下PMVM 的径向和切向气隙磁密进行傅里叶分解，得到12 槽20 极PMVM 径向和切向气隙磁密主要谐波幅值和相位如图7 所示，其中气隙磁密的Pr(10 次) 谐波分量占主要成分，其次，|Ns-Pr|(2 次)、|Ns+Ps|(14 次)和|Ns+Pr|(22 次)谐波分量的幅值也相对较大，表明PMVM 存在显著的气隙磁场调制效应。由图7c 和图7d 可以看出，不同次数的气隙磁密谐波的旋转方向有所不同，其中2 次、14 次谐波与10 次、22 次谐波具有相反的旋转方向。气隙磁密各次谐波的径向和切向分量间的相位差基本保持不变，气隙磁密10 次谐波的径向和切向分量的相位差为75°，而2 次、14 次和22次谐波的径向和切向分量的相位差均为270°。

图7 径向和切向气隙磁密谐波特性

图8 为气隙磁密主要谐波贡献的电磁转矩分量波形，PMVM 主要谐波贡献转矩占比如表4 所示。PMVM 的总平均转矩为5.126 N·m，气隙磁密10 次谐波产生的电磁转矩为5.026 N·m，占总平均转矩的98%，而其他气隙磁密谐波贡献电磁转矩占比较低，基本可忽略。考虑到电机漏磁和磁饱和等因素，误差在合理范围内。因此，12 槽/20 极PMVM 仅气隙磁密10 次谐波可产生稳定电磁转矩。

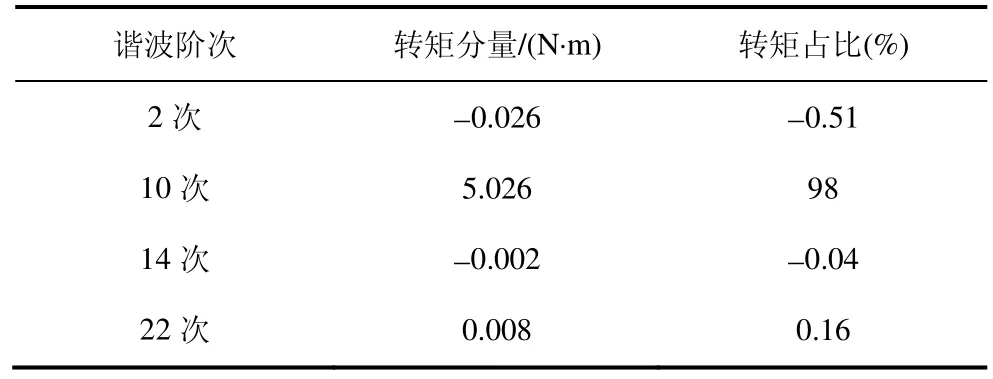
表4 PMVM 主要谐波贡献转矩分量占比

图8 PMVM 主要谐波贡献转矩分量波形

5 不同结构参数下气隙磁场调制效应

为探究PMVM 气隙磁场调制效应受定子磁导调制函数的影响，选择定子极弧系数θs分析气隙磁场谐波及其贡献的电磁转矩分量的变化规律。不同定子极弧系数θs下PMVM 气隙磁密谐波和定子磁导谐波变化情况如图9 所示。首先，随着θs的增大，定子磁导直流分量增加，而定子磁导Ns(12 次)谐波分量占比降低，气隙磁场调制效应削弱。径向永磁气隙磁密Pr(10 次)谐波在定子磁导的调制作用下产生|Pr-Ns|(2 次)谐波。因此，随着θs的增大，径向永磁气隙磁密Pr(10 次)谐波增大，而径向永磁气隙磁密|Pr-Ns|(2 次)谐波却显著减小。

图9 不同定子极弧系数下磁场调制效应

由气隙磁密|Pr-Ns|(2 次)和Pr(10 次)谐波贡献的电磁转矩如图10 所示。随着θs的增大，切向气隙磁密Pr(10 次)谐波减小，由气隙磁密Pr(10 次)谐波所产生的电磁转矩分量逐渐降低，导致PMVM 平均转矩也随之降低，表明PMVM 气隙磁场调制效应对电机转矩性能影响较大，而PMVM 的定子槽结构参数对改善气隙磁场调制效应至关重要。

图10 不同定子极弧系数下平均转矩

6 结论

基于气隙磁场调制理论，从永磁磁场和电枢反应磁场谐波耦合的角度，揭示了永磁游标电机的气隙磁场调制效应和转矩产生机理。选取永磁游标电机转矩性能作为优化目标，结合响应面法和遗传算法对电机转矩性能进行优化。为验证多目标优化结果的可行性，对比优化前后电机的电磁转矩和齿槽转矩，优化后的PMVM 的平均转矩增加了0.7%，转矩脉动减少了10.9%，齿槽转矩减少了77.3%。采用麦克斯韦应力张量法定量分析了PMVM 气隙磁密谐波对电磁转矩的贡献，结果表明PMVM 电磁转矩仅由单一气隙磁密工作谐波产生。通过分析PMVM 在不同定子极弧系数下的气隙磁密谐波，研究定子槽结构参数对永磁游标电机气隙磁场调制效应的影响规律，为进一步提高永磁游标电机转矩性能提供了理论依据。