压力容器碟形封头焊接结构应力数值计算及安全评定

代文广,周广涛,余作恒

(1.厦门宏发电力电器有限公司,厦门 361021;2.华侨大学机电及自动化学院,厦门 361021;3.致微(厦门)仪器有限公司研究生工作站,厦门 361021)

0 引 言

埋弧焊具有生产效率高、焊缝质量好、节省焊接材料与电能等显著优势,成为工业生产中最常用的焊接方法之一,被广泛应用于化工容器、锅炉、船舶、桥梁等金属结构的焊接。压力容器一般由壳体、封头、法兰、密封元件、支座、开孔和接管等部件组成,在石油化工、能源、核电等重要领域应用广泛。在服役过程中受到密封、承压、介质等因素影响,压力容器易发生爆炸、燃烧等安全事故,造成巨大的人员伤亡、环境污染和财产损失。为减少安全事故的发生,压力容器在设计及制造中必须遵守相关标准和规范[1]。目前,全球压力容器分析设计规范总体分为ASME VIII-2和EN 13445两大体系,其中,ASME VIII-2规范是基于第四强度理论(畸变能理论[2])对当量应力进行评定。根据ASME VIII-2,在压力容器壳体、封头等关键部位上开孔并接管时,其开孔区域易产生复杂的应力状态,从而破坏结构连续性,减弱壳体强度,使得壳体与接管连接区域出现应力集中[3];壳体上产生的局部高应力将严重影响其承载能力,从而成为设备的破坏源。因此,对开孔部位作较详细的应力分析和强度评定是确保压力容器安全运行必不可少的内容[4-5]。

某型压力容器采用常见的碟形封头,其碟形封头组合件之间采用埋弧焊焊接。为对该型压力容器在工作条件下的结构应力情况进行安全校核,作者采用有限元分析方法,对其碟形封头焊接组合件进行应力场数值模拟计算,根据模拟结果确定较大应力点并进行试验验证,并根据ASME VIII-2中各应力与许用应力的对应关系对碟形封头进行应力评定,以期能丰富压力容器安全校核方面的理论体系,为相关企业在压力容器的优化设计方面提供理论指导。

1 试验方法与结果

某型压力容器碟形封头材料为SA-240M 304不锈钢,工作温度为148 ℃,工作应力为0.35 MPa,设计许用应力为103 MPa,屈服强度为205 MPa,抗拉强度为515 MPa。碟形封头结构如图1所示,由上(上盖)、下(侧壁)两部分焊接而成。上盖厚度为4 mm,侧壁内壁中部球径为425 mm,边缘过渡圆角半径为42.5 mm,内壁最大口直径为425 mm,壁厚为4 mm。焊接工艺如下:采用机加工方法在上盖、侧壁两部分上加工Y型坡口并装配,背面加贴陶瓷衬垫,采用KAIYUAN MZC-1250型埋弧自动焊机进行焊接,焊接电流为385 A,电压为32 V,焊接速度为68 mm·min-1。目视检验,确保焊接结构正、背面焊缝表面均无裂纹、气孔、夹渣、未熔合、明显的焊瘤和咬边等缺陷。

对焊接接头进行砂纸打磨、抛光后,在母材和接头(垂直于焊缝)处截取如图2所示的拉伸试样,对焊缝进行铣平处理。由图3可见:接头屈服强度与母材相近,均为260 MPa左右,断后伸长率与抗拉强度略低于母材。由此可知,可将碟形封头焊接件作为一个整体进行有限元模拟。

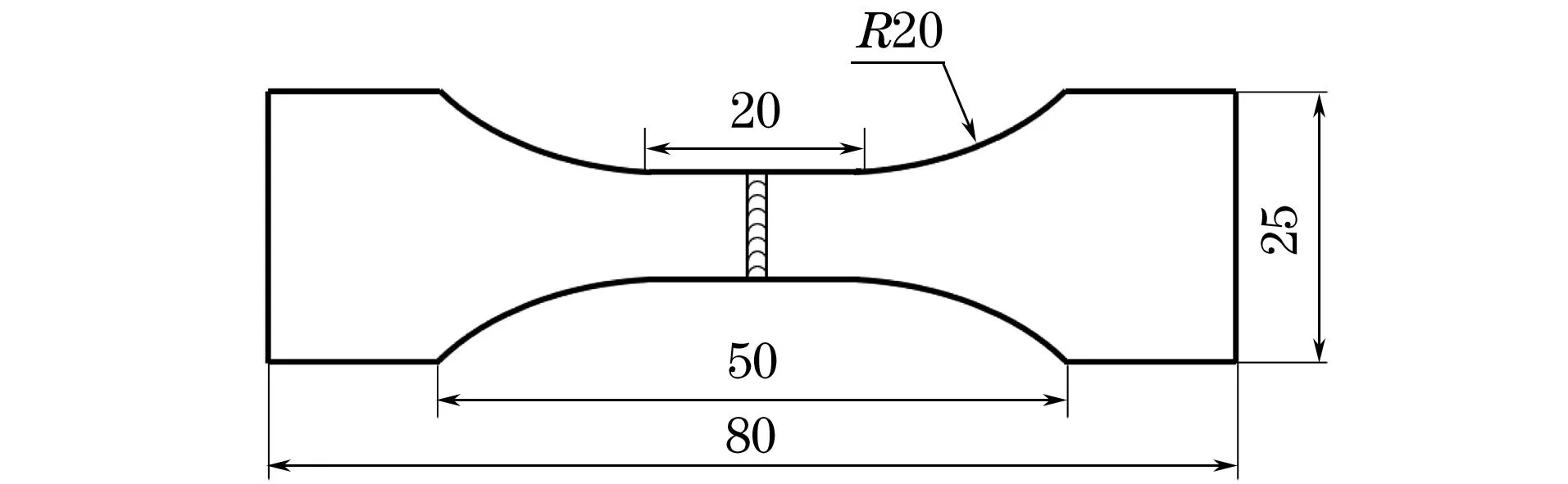
图2 拉伸试样的形状和尺寸Fig.2 Shape and size of tensile specimen

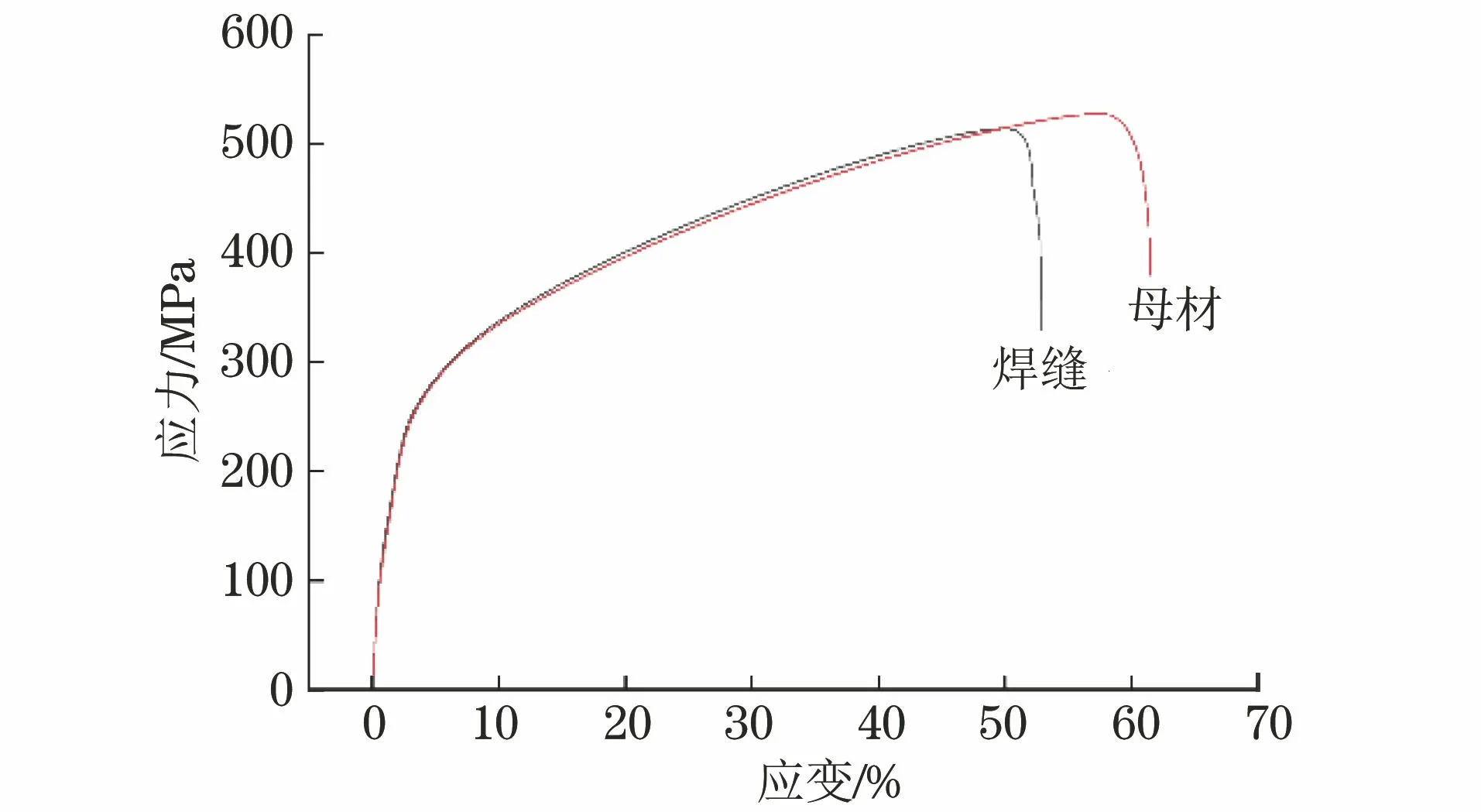
图3 焊缝与母材的拉伸应力-应变曲线Fig.3 Tensile stress-strain curves of weld and base material

2 应力校核理论基础

在结构应力校核前,需计算结构件各处的当量应力,从而与许用应力进行比较,以确定该结构件是否适合预期设计条件。当量应力Se是由各应力分量采用Von Mises屈服准则得到的应力度量,计算公式[6-7]如下:

(1)

式中:σ1,σ2,σ3分别为第一、第二、第三主应力。

应力线性化是基于板壳理论,应用于压力容器强度校核的一种方法,主要包括应力积分法、以节点力为基础的结构应力法和以应力积分为基础的结构应力法3种,其中应力积分法是目前最常用的方法。应力线性化就是将沿着应力分类线的实际应力按照合力和合力矩等效原理分为薄膜应力σij,m、弯曲应力σij,b、峰值应力σij,F(x)丨x=t[8-10]。薄膜应力是沿着应力分类线每一应力分量的平均值,弯曲应力由沿应力分类线的各应力分量的线性变化部分组成,峰值应力为非线性部分,表达式分别为

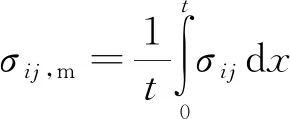
(2)

(3)

σij,F(x)丨x=t=σij(x)丨x=t-(σij,m+σij,b)

(4)

式中:σij为应力分类线上某点的应力张量;t为应力分类线长度,即壁厚;x为沿应力分类线距外壁距离。

3 有限元模拟与试验验证

3.1 有限元网格模型建立

该型压力容器碟形封头的三维模型如图4(a)所示,该三维模型的尺寸与实际尺寸相同,同样以插销联动的形式对封头进行固定,8个销轴通过旋转分别进入8个封头长圆孔右侧区域,与长圆孔中心处径向夹角为30°。采用MSC.Marc非线性有限元仿真软件建立碟形封头有限元网格模型,如图4(b)所示,网格划分采用疏密过渡的形式,可能产生应力集中的8个长圆孔区域的网格划分较密,其他区域较稀疏。共计68 448个网格单元,92 742个节点,单元类型为八节点六面体单元,在厚度方向上分为3层。

图4 碟形封头的三维模型及有限元网格模型Fig.4 Three dimensional model (a) and finite element mesh model (b) of dished closure head

3.2 边界条件

碟形封头的边界条件包括位移边界条件和载荷边界条件。实际工作中,封头的固定由联轴销施加,当采用刚体面约束作为位移边界条件时,该刚体的形状和作用区域与联轴销实际尺寸相吻合,如图5所示,计算得到等效应力值为122.7 MPa。载荷边界条件是上盖内表面圆弧半径为425 mm的顶部和42.5 mm过渡位置处0.35 MPa的均布压力,模拟的是实际工况中的气压加载。

图5 联轴销三维模型和刚体面约束模型Fig.5 Three dimensional model of coupling pin (a) and rigid face constraint model (b)

3.3 应力状态模拟及验证

由图6可知:碟形封头的长圆孔右侧圆弧中间区域的Mises等效应力最大,达到139.8 MPa,为危险区域,这是因为该区域是被联轴销固定的位置,且联轴销对封头采取右侧偏置约束,所以长圆孔右侧圆弧的Mises等效应力大于左侧。

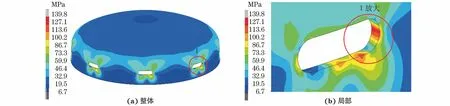
图6 模拟得到碟形封头Mises等效应力云图Fig.6 Simulated Mises equivalent stress nephogram of dished closure head: (a) complete sample and (b) local zoom

在拉伸过程中采用应变片测试危险区域应变,应变片采用45°应变花形式,分别测试0°,45°,90°方向的主应变εx,ε45,εy。测试得到危险区域,即长圆孔右侧圆弧中间外壁应变εx,εy,ε45分别为0.002 3,0.001 2,0.001 6,内壁应变εx,εy,ε45分别为0.002 4,0.001 2,0.001 7。根据以上数据可以计算出薄膜应力σm,计算公式如下:

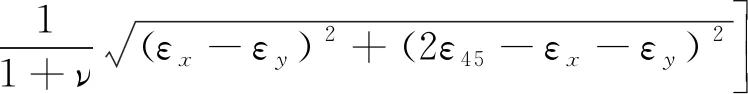
(5)

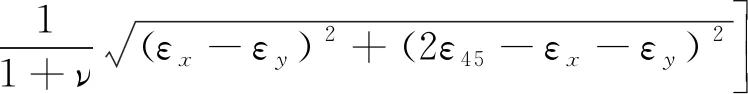
(6)

(7)

式中:E为弹性模量;ν为泊松比。

计算可得右侧圆弧中间区域的外壁,内壁薄膜应力分别为133.2,134.1 MPa。Mises等效应力为3个主应力方向的综合应力,薄膜应力为平面应力,即2个主应力方向的综合应力,但由于该处壁厚较小,且内外壁薄膜应力相差较小,因此厚度方向的应力可以忽略。试验结果与模拟结果(139.8 MPa)的相对误差仅为4.7%左右,验证了应力模拟的有效性。

4 应力安全评定

有限元模拟得到碟形封头的法向应力分布如图7所示。碟形封头应力评定前需要对危险区域的法向应力进行等效线性化处理,这是因为有限元模拟得到的法向应力结果为总应力,等效线性化的目的就是将总应力进行分解。先根据应力分类法将应力分类线上的法向应力分为一次局部薄膜应力Pl、一次弯曲应力Pb和峰值应力F;而由于封头上的8个长圆孔属于结构不连续区域,封头内部还存在由温度引起的二次弯曲应力Q[11]。二次应力为由温度引起的热应力,与力学载荷无关,因此不存在二次薄膜应力和二次峰值应力。二次应力模拟方法与一次应力不同,将模型加热至工艺温度(148 ℃)并保温,按同样方法进行应力线性化处理。

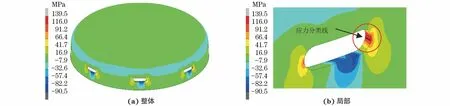
图7 模拟得到碟形封头法向应力云图Fig.7 Simulated normal stress nephogram of dished closure head: (a) complete sample and (b) local zoom

结合式(2)～(4), 图8为危险区域应力分类线上法向应力的等效线性化结果。可知,一次局部薄膜应力、一次弯曲应力、峰值应力、二次弯曲应力分别为135.19,3.54,0.774,42.83 MPa。根据ASME VIII-2对一次、二次应力进行安全评定,评定条件为

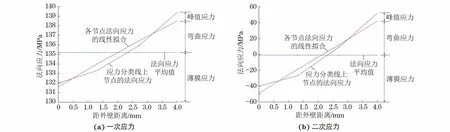
图8 碟形封头危险区域法向应力的等效线性化结果沿应力分类线(从外壁到内壁)的分布Fig.8 Equivalent linearization results distribution along stress classification line (from outer wall to inner wall)of normal stress in dangerous region of dished closure head: (a) primary stress and (b) secondary stress

Pl≤1.5S

(8)

Pl+Pb+Q≤3S

(9)

式中:S为设计温度下304不锈钢的许用应力,103 MPa。

根据式(8)、式(9)可得其评定安全。

5 结 论

(1) 采用所建立的有限元模型模拟得到的SA-240M 304不锈钢埋弧焊碟型封头的长圆孔右侧圆弧中间区域的Mises等效应力最大,为危险区域,与由实测应变计算得到应力的相对误差仅为4.7%,验证了模型的准确性。

(2) 根据ASME VIII-2对危险区域沿应力分类线的法向应力进行等效线性化处理,得到埋弧焊碟型封头一次薄膜应力、一次弯曲应力、峰值应力、二次弯曲应力分别为135.19,3.54,0.774,42.83 MPa,评定为安全。