数形结合思想在二次函数问题中的巧用
2024-01-12谢成强
谢成强



【摘 要】 二次函数的图象与性质是中考的必考内容.二次函数是数形结合的好素材,考查学生画图、识图、用图的能力,考查学生数据处理能力和数学运算能力.
【关键词】 初中数学;数形结合;二次函数
二次函数是中学数学的重要内容,其很多性质都在图象上得以呈现.正如华罗庚说“数无形时少直觉,形少数时难入微”,二次函数的图象会告诉我们二次函数系数之间的关系以及更多的有用信息.本文分类剖析数形结合思想在二次函数问题中的应用.
1 利用二次函数图象求参数范围
例1 (2022·四川南充)已知点在抛物线上,当且时,都有,则m的取值范围为( )
(A). (B). (C). (D).
分析 根据题意可得,抛物线的对称轴为,然后分四种情况进行讨论分析,最后进行综合即可得出结果.
解析 根据题意可得,抛物线的对称轴为,
①当0<m<时,恒成立;
②当时,恒不成立;
③当时,使恒成立,
∴m,
∴m,,
④当时,恒不成立;
综上可得:,故选(A).
点评 本题考查抛物线与点的关系,考查二次函数的基本性质,学会从题目中提取有用信息,熟练掌握二次函數的基本性质是解决本题的关键.
2 利用二次函数图象解决代数式的最值问题
例2 (2022·凉山州)已知实数a、b满足a﹣b2=4,则代数式a2﹣3b2+a﹣14的最小值是 .
分析 根据a﹣b2=4得出b2=a﹣4,代入代数式a2﹣3b2+a﹣14中,然后结合二次函数的性质即可得到答案.
解析 ∵a﹣b2=4,
∴b2=a﹣4,
∴原式=a2﹣3(a﹣4)+a﹣14
=a2﹣3a+12+a﹣14
=a2﹣2a﹣2
=a2﹣2a+1﹣1﹣2
=(a﹣1)2﹣3.
∵1>0,
又∵b2=a﹣4≥0,
∴a≥4,
∵1>0,
∴当a≥4时,原式的值随着a的增大而增大,
∴当a=4时,原式取最小值为6,
故答案为:6.
点评 本题巧妙之处就在于:从求代数式的最值问题联想到二次函数的最值.解题的关键是灵活掌握配方法,熟练运用代数式的性质,完成本题.
3 利用函数图象确定其他函数图象
例3 (2020自贡)函数与y=ax2+bx+c的图象如图1所示,则函数y=kx﹣b的大致图象为( )
图1
(A)(B)(C)(D)
分析 先利用已知图中的反比例图象判断k的符号,利用二次函数图象判断b的符号,即可判断正误.
解析 根据反比例函数的图象位于一、三象限知k>0,
根据二次函数的图象,知a<0,b<0,
∴函数y=kx﹣b的大致图象经过一、二、三象限,
因此本题选(D).
点评 本题考查了反比例、一次函数、二次函数的图象与性质等知识,考查二次函数的顶点坐标、开口方向和对称轴等.
4 利用两个图象的交点个数求参数范围
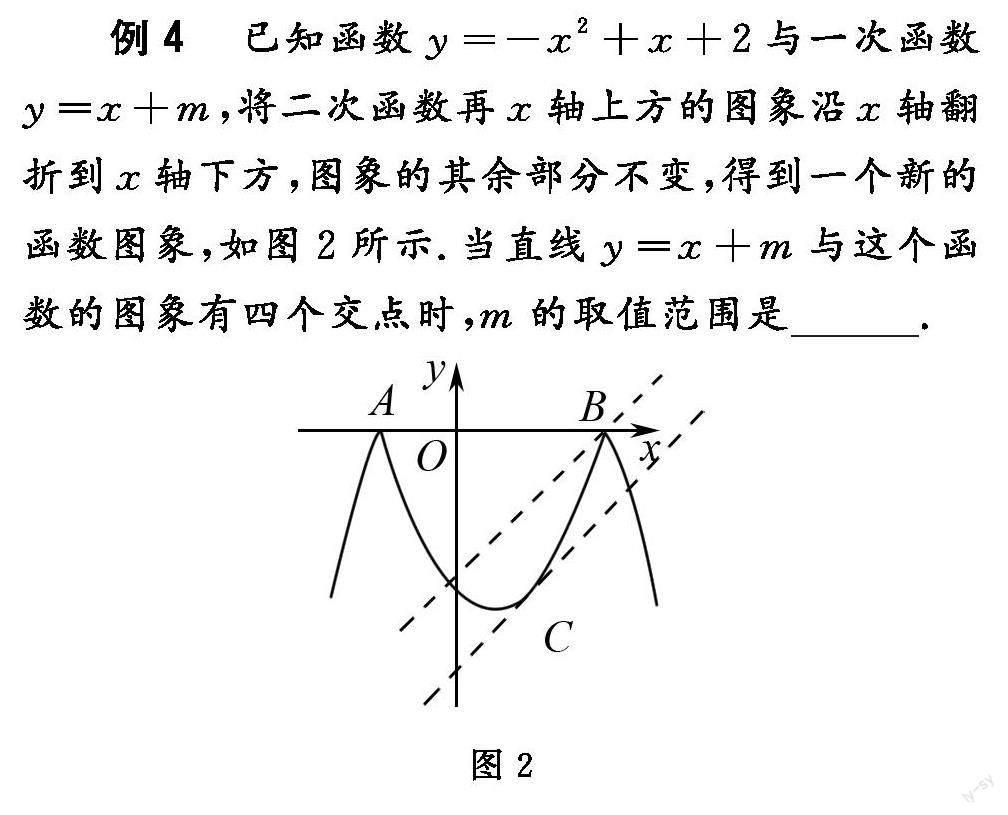
例4 已知函数y=-|﹣x2+x+2|与一次函数y=x+m,当直线y=x+m与这个函数的图象有四个交点时,m的取值范围是_______.
分析 函数y=-|﹣x2+x+2|的图象是将二次函数y=﹣x2+x+2在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新的函数图象,如图2所示,过点B作直线y=x+m1,将直线向下平移到恰在点C处相切,则一次函数y=x+m在两条直线之间时,两个图象有4个交点,即可求解.
解析 如图所示,过点B作直线y=x+m1,将直线向下平移到恰在点C处相切,
则一次函数y=x+m在两条直线之间时,两个图象有4个交点,
令y=﹣x2+x+2=0,解得:x=﹣1或2,即点B坐标(2,0),
翻折抛物线的表达式为:y=(x﹣2)(x+1)=x2﹣x﹣2,
将一次函数与二次函数表达式联立并整理得:x2﹣2x﹣2﹣m=0,
由Δ=b2﹣4ac=4+4(2+m)=0,解得:m=﹣3,
当一次函数过点B时,将点B坐标代入y=x+m,得0=2+m,则m=﹣2.
点评 本题是二次函数图象与其他函数图象相结合问题,解决此问题时,先作出函数图象,结合两个函数的图象,求解参数范围.
5 由二次函数图象判断二次函数系数关系
例5 (2022·湖北随州)如图3,已知开口向下的抛物线与x轴交于点对称轴为直线.则下列结论:①;②;③函数的最大值为;④若关于x的方数无实数根,则.正确的有( )
图3
(A)1个. (B)2个. (C)3个. (D)4个.
分析 根据二次函数的图象,结合二次函数的对称轴和顶点坐标的性质得出a,b,c的关系.
解析 由图象可知,图象开口向下,a<0,对称轴为x=1,故,故b>0,且,则,故②正确.
∵图象与y轴的交点为正半轴,∴c>0,则abc<0,故①错误.
由图象可知当x=1时,函数取最大值,将x=1,代入,中得:,
由图象可知函数与x轴交点为(﹣1,0),对称轴为x=1,故函数图象与x轴的另一交点为(3,0),
设函数解析式为:,
将交点坐标代入得:,故化简得:,
将x=1,代入可得:,故函数的最大值为-4a,故③正确.
变形为:要使方程无实数根,
则,将c=-3a,,代入得:,
因为a<0,则,则,
综上所述,因此④正确.
所以②③④正确,故选(C).
点评 本题主要考查二次函数的交点式和一般式,同时考查二次函数的最值,对称轴及交点坐标,数形结合思想化解本题的难点.根据二次函数的图象与性质,对四个结论逐一判断即可.
