江苏新高考再选科目赋分方案评析与仿真研究*

仝 虎 刘明岩

自2014 年《国务院关于深化考试招生制度改革的实施意见》[1]颁布至今，已经有29 个省（市、自治区）分五批启动新高考改革。其中第四、第五批改革省份和第三批省市方案基本相同。江苏省作为第三批新高考改革8 个省市之一，在总结吸取前两批改革省市经验的基础上采用了“3+1+2”模式[2]。新高考改革最大的亮点是取消文理分科，考生可根据自身兴趣爱好、个性特长和高校专业对选考科目设置的要求，自主选择考试科目，在共性基础上强调体现学生的个性化与差异性。然而，伴随着科目选择的自主性增强，新高考在实施过程中也遇到了一些问题，这些问题大多和选考科目赋分方式有关。本文从分析等级赋分方式引发的问题入手，对江苏再选科目赋分方案及学者们提出的优化改进方案进行评析，并进行数据模拟仿真演算。

一、等级赋分方式问题探究

新高考改革方案中，由于学生可以自主选择3 门科目并计入高考总分，计分方式成为大家关注的重心和焦点。为实现不同科目间的可比可加，新高考为选考科目设计了等级赋分方案。但自新高考改革试点启动以来，等级赋分方案开始显露出自身的局限性。以第一批试点省市为例，等级赋分方案如下：浙江方案对选考科目设置21 等级，赋分区间为[40-100]；上海方案设置11 等级，赋分区间为[40-70]。两地设置的等级间隔均为3 分，各等级人数所占比例的分布有均匀性、对称性的特征。两个试点省市在改革方案实施第一年暴露的问题，主要有以下四个。

问题一是选考科目在总分中权重过低。必考科目语数外3 科按原始分计，每门150 分。浙江方案中选考科目分数区间[40-100]，分数全距为60 分；上海方案中分数区间[40-70]，分数全距只有30 分。朱邦芬院士指出，浙江方案中，物理成绩对高考总成绩的贡献率只有60/750=8%，而外语的权重为150/750=20%，二者相差非常之大。上海方案中也存在同样情况，物理成绩对高考总成绩的贡献率只有30/660=4.5%，外语的权重为150/660=22.5%。一门外语考试成绩对于升学的贡献，等于5 门物理，远远超过物理、化学、生物等3门科学课程之和[3]。这样的制度设计导致选考科目地位大大被轻视和弱化。从高校招生的角度来看，一门物理科所携带的信号可能还比不过数学英语卷中一道题目来得重要[4]。

问题二是等级划分和比例设置科学性不足[5]。不同选考科目之间的难易程度有差异，由于选择的灵活性，考生人数大不相同，考生群体水平大概率存在差异，其考试成绩分布必然会不同。而现行的等级分方案，为了破解不同科目的不等值问题，使科目成绩具有可比性和可加性，提前对选考科目的原始分强行划分等级和比例，所有选考科目都依照这个标准执行。这就相当于把所有选考科目成绩都转化成了相同的分布形态，这本身就缺乏合理的科学依据，这种处理方法在摆平各科难度的同时，也抹平了各科考生群体能力的差异[6]。有关研究认为五个等级的划分是合适的[7]，但各等级比例的赋值具有一定的人为性。具体到浙江、上海方案，其等级比例的赋值呈均匀性、对称性，这符合正态分布的特点。而相关研究显示，学生成绩并非一定服从正态分布，大体上是：对同一考生群体，难度低的科目成绩呈负偏态，难度高的科目成绩呈正偏态；对相同难度的科目，水平高的考生群体成绩呈负偏态，水平低的考生群体呈正偏态[8-9]。这种强制按正态分布赋等级比例的做法并不严谨，缺乏科学依据，带有一定的人为性和随意性。

问题三是等级边界相隔3 分的设计充满隐患。浙江、上海两地在给各等级赋分时，为了淡化考生“分分计较”的观念，为每个等级赋了一个固定分数，且相邻等级间相隔3 分。这种设计存在很大的公平隐患。对于高考这种全民关注的高利害考试，最终以总分来排名录取，考生必然会分分计较。实际情形中，由于考生数量巨大、成绩分布呈现两边疏、中间密的特征，在成绩分布密集区域，同分会大量出现，1 分可能会超过千人，而处于两个等级边界的考生群体，原始成绩的1 分之差，却导致等级成绩出现3 分的差距。这个等级成绩计入高考总分，必然会导致不公平现象。换言之，选考科目的原始成绩少1 分，就很可能需要语数外成绩多3 分来弥补。另外，因为考生可以选择3 门科目，在极端的情况下，这种情形还会被放大。例如：两个水平相当的考生A 和B，选择了3 门相同的选考科目，B 的每门科目原始成绩都恰好比A 低1 分，且都恰好位于边界分，3 门选考科目成绩都被划分到低一级的等级，这样就导致B 的3 门选考科目总成绩原始分只比A少3 分，而转换后的等级分却比A 少9 分，如此结果显然是不公平的。

问题四是“物化遇冷”，考生“弃理选文”“避强邻弱”等功利化选科现象迅速蔓延。这个问题是由前序问题引发而来的，具有因果关系。正如问题二所描述的，在各学科考生成绩分布形态相同或相似的情况下，按事先定好的等级和比例标准来切割不同科目考生群体的方法是可行的。但实际情况是，不同选考科目之间的难易程度有差异，选考群体的数量和能力水平也大不相同，所以科目考试成绩的分布形态必然会有较大的差异。在这种情况下，不考虑科目实际难度，也不考虑选考群体水平差异，而只追求形式上的可比，仍用固定的等级赋分方式来处理，不但会强行抹平不同科目之间的难度差异，而且会强行抹平不同考生群体水平间的差异。举例说明，同样是100 分的试卷，一个大学生得满分和小学生得满分代表的难度是不一样的，大学生不论是从认知水平、理解能力，还是需要掌握知识的难度，与小学生都不能同日而语。但按新高考计分方式，会得出大学生和小学生得分一样、水平一样的结果。

这样的结果，忽略了两个群体之间存在的差异，忽视了试卷的难度，显然不合理。由于考生的转换分数与其在该科目当中的排名相关，两个人选修了不同的科目，只要在相同的排位水平，不管原始成绩是多少，高考的选考科目就会得到相同的分数。在这种计分模式下，学生为了追求自身利益最大化，在选科时大概率不会从自身兴趣出发，而是以分数目标为导向，去计算选择哪个科目对自身更有利。家长、学校为了自身的利益和声誉也会鼓励学生去这么做。因此，出现“物化遇冷”“避难选易”“避强邻弱”等现象也就不足为奇了。据陈爱文、胡银泉对浙江省选考情况的粗略调查[10]，2016 级高中生在2017 年选定选考科目时，某中学近千人中只有7 个学生选考物理；某一级普通高中特色示范学校也只有不到50 人选考物理；某县所有中学只有不到100 人选考物理；某市2016 级约一万名学生，只有不到900 名学生选考物理。这些现象虽然仍在动态变化中，但“惧选物理”的情绪由落后地域向发达地域、由二级普通高中特色示范学校向一级普通高中特色示范学校快速蔓延。这种选科结果已经严重背离高考改革者的初衷，从长远来看，学生、学校、社会三方无一赢家。

江苏省作为第三批改革省份采用“3+1+2”模式：必考科目语文、数学、外语每门150 分计入总分；选考科目每门均为100 分，其中首选科目（物理、历史）以原始分计入总分，再选科目（化学、生物、思想政治、地理）以等级分计入总分，等级分赋分起点为30 分，满分为100 分。再选科目等级分具体转换规则和步骤[11]如下：第一步，按照考生原始分从高到低划定A、B、C、D、E 共五个等级，各等级人数所占比例分别约为15%、35%、35%、13%和2%。第二步，将A 至E 五个等级内的考生原始分，依照等比例转换法则，分别对应转换到100～86、85～71、70～56、55～41 和40～30 五个分数段，从而将考生的原始分转换成为等级分。江苏省采用的选考科目计分方案已有很大进步：首选科目（物理、历史）以原始分计入总分，分数全距为100 分，再选科目（化学、生物、思想政治、地理）赋分范围从30 至100，分数全距为70 分。相比于前期改革省市，江苏省的选考科目在总分中的比重有所增加；五个等级的比例分布非均匀有负偏态倾向，更加符合考生实际成绩分布特征；在原始分转换成等级分时使用等比例转换方式规避了等级间隔3 分的隐患。这些都是吸取前期试点经验进行优化改进的地方，值得充分肯定。江苏现行的等级计分方案在一定程度上缓解了考生“弃理选文”“避强邻弱”“田忌赛马”等功利性选科的问题，但在等级赋分具体操作和执行上，以及在对考生的选考指导方面，还有进一步优化的空间。

二、保障机制的优化改进

针对“弃理选文”“避强邻弱”等考生功利性选科问题，现有的应对措施主要是政策引导。比如在解决“物理遇冷”问题时，浙江、上海都推出了物理选考科目保障机制，浙江的物理保障基数为6.5 万人，上海的物理保障基数为1.5 万人，如果物理选考人数低于保障基数，在计算考生的物理等级分时将用保障基数替代实际选考人数。朱明宇的研究指出物理保障机制存在不足之处[12]：一是阈值人数设定不够严谨，将阈值人数设定为本科理工类专业每年在本省市招生的计划数不够严谨，因为选择物理的考生并非全部报考本科理工类专业，并且每年考生人数呈现动态变化，每年的保障人数都无法确定；二是填充基数的方式缺乏科学性，保障机制的修正策略仅参考选考人数，未与考生能力分布建立联系，注定其必然出现“纠偏失策”；三是将物理保障机制扩展至其他选考科目，普适性存疑。也有学者对不同条件下物理科目保障机制的运行结果模拟研究后指出[13]：在学生群体成绩呈正态分布或正偏态分布情况下，保障机制能够吸引很多学生加入选科；当学生群体成绩呈负偏态分布时，保障机制对最优学生和最差学生更为有利，对中等水平或中高水平的学生作用很小。然而需要启动保障机制的，恰恰是呈负偏态分布的物理科目。这种情况下，保障机制所能起到的作用十分有限，它可以保障一定的考生数量，但无法保障考生质量，无法吸引真正对物理科目有兴趣的中高水平考生，却会吸引一些低水平学生的“投机报考”。

江苏省的“3+1+2”模式虽然很好地解决了“物理遇冷”问题，选考物理的比例逐年提高，但又出现了化学选考人数下降的问题。针对此问题，江苏省在参照浙江、上海物理保障机制的基础上推出了再选科目保障机制[14]，使用保障比例替代保障基数。首先在化学科目上执行了保障机制，依据相关学科（专业）对化学科目选考要求和全国高校近5 年面向江苏的招生计划数进行测算，以当年高考总实考人数的25%作为化学科目划分等级比例的基数。再选科目保障机制用保障比例替代保障基数，化静态保障基数为动态保障基数，规避了静态保障基数带来的弊端，比浙江、上海的物理保障机制更进了一步，但其修正策略依然只是填充基数，未与选考科目考生群体能力分布建立联系，“纠偏失策”的情况依旧可能存在。范美琴在肯定江苏再选科目保障机制的积极作用的同时指出：“在快速缓解眼前矛盾的同时，还须加强对不同再选科目赋分弹性机制的研究，使得现行赋分办法对流动现状下的选考群体有更强的适应性和纠偏功能。”[15]所以，对再选科目保障机制和等级计分方式进一步改进和完善是今后的方向。

三、等级赋分校准方案评析

针对现行等级赋分方式暴露出来的“理化遇冷”“避难就易”“避强邻弱”等功利性的选科问题，许多学者从技术角度提出了赋分改进方案。根据出发点不同，主要分为两类：

第一类是学业质量水平参照划等法。即制定学科统一标准，以学业水平质量为参照，把现在学业水平考试的常模参照计分方式改为质量水平参照计分方式。诸多专家学者都提到过这个办法[16-18]，这是一劳永逸的理想解决方案，但方案实施难度很大，对改革者的专业要求很高，成本也很高，目前国内时机、条件都不具备。

第二类是对现有等级赋分方式进行校准的方案。根据校准参照不同，又细分为以选考人数为参照、以学业水平合格考试成绩为参照、以必考科目成绩为参照三种。以下笔者对这三种校准方案做简要评析。

（一）以选考人数为参照的校准方案

杨燕燕撰文指出新高考选科失衡的主要原因在于现行等级赋分方式是静态赋分[19]，静态赋分体现在两方面：（1）固定的等级划分；（2）各等级既定不变的人数比例。该文认为选考科目学科本身的难度和高校对于学科的限定性要求等因素会影响学生的选科，既然各选考科目实际选考人数和科目难度有关，便可以根据各科目的实际选考人数来衡量学科间不同的难度等级。为此，该文提出“改静为动”的修正方案，以选考人数为参照来判定科目难度等级并给出科目难度系数，然后根据科目难度系数动态调整各等级的人数比例。笔者认为，“改静为动”的思路很新颖，让人眼前一亮，但以选考人数为参照、利用选考人数来判定选考科目的难度差异，既不科学也不稳定。并且，各科选考人数比例是动态的，每年都在变动，有其不稳定性，可以用来定性，但不能用来定量和计算。

（二）以学业水平合格性考试成绩为参照的校准方案

一些学者提出以学业水平合格性考试成绩为参照，对选考科目等级划分和成绩进行校准修正，具体细节做法又有所不同。比如，周文阔提出利用“合格考样本”作为参考样本，计算出相应的合格考“修正分数”，以此对选考科目等级分进行补充和调整[20]；张华提出以选考科目的合格考平均成绩为参照，计算选考科目的“可比系数”，利用“可比系数”来衡量不同选考科目群体之间的水平差异，以此对考生等级分进行校准[21]；李金波提出以学业水平合格考成绩为参照，对各等级选考学生的固定比例进行调整，变固定占比为可变占比[22]。这些校准调整方法各不相同，但都以合格考成绩为参照，因此归为一类。诚然，学业水平合格考是所有学生都要参加的考试，但其与高考有着本质的区别：学业水平合格性考试的难度较低，难度系数通常控制在0.8 左右，而高考属选拔性考试，难度系数一般在0.6 左右[23]，两者定位不同，并且合格考与高考时间通常不一致。因此，使用合格考成绩为参照的各种校准方法并不合适。

（三）以必考科目成绩为参照的校准方案

温忠麟提出一种基于正相关假设理论使用必考科目统考成绩对选考科目进行统计校准的方案，有一定现实意义[24]，但其计算过程较为复杂；随后，针对一些问题和质疑，他又发文做了澄清和解释[25]，并提出校准方案的多种简单变式，使校准方案具备了很强的指导意义和实践意义。黄恕伯提出依据必考科目成绩为选考科目分指标（FZB）的方案[26]有着相似的思路。

笔者认为，以必考科目统考成绩为参照对选考科目进行校准的方案是可行的，其科学依据和理论基础主要有以下两个：

（1）加德纳多元智能理论[27]。哈佛大学认知心理学家加德纳提出的多元智能理论认为人类拥有九种智能：语言、数理逻辑、空间想象、身体运动、音乐节奏、人际交往、内省、自然探索和存在感知。根据加德纳多元智能理论可以发现，高考必考科目（语文、数学、外语）考查的主要是语言、数理逻辑、空间想象的能力；选考科目（物理、历史、化学、生物、思想政治、地理）考查的内容也以语言、数理逻辑、空间想象为主。因此，除了音乐、体育、美术以外，可以假设考生的选考科目能力分布与必考科目（语数外作为整体）的能力分布相同或相近。

（2）相关性理论[28]。相关性分析是分析客观事物之间相关性的数量分析方法，研究两个变量间的线性相关问题称为线性相关分析，两个变量间的相关程度强弱用相关系数r 来描述。r 的取值范围为[-1，1]，r>0 表示两个变量为正相关，r<0 表示两个变量为负相关，r 绝对值越大，表示两变量间的相关程度越密切。在研究两个变量之间的线性相关程度时通常采用Pearson 相关性分析法。Pearson 方法中相关系数r 的计算方法参见公式1，其中n 为样本数量，xi、yi分别为两个变量的取值，表示两个变量的算术平均值。必考科目成绩能对选考科目成绩进行校准的相关性理论依据是：对于同一考生群体，选考科目成绩与必考科目成绩之间呈正相关。当选考科目与必考科目的相关系数r 取值在介于0.3 与0.95 之间，使用必考科目校准选考科目则是可行的，并且在这个范围内，r 取值越大，校准精度越高[29]。

笔者选取江苏新高考改革后连续两年（2021 年、2022 年）的考生高考成绩，计算各科目之间的相关性，得到化学、生物、思想政治、地理四门科目与语数外科目之间相关系数表（详见表1）。由表1 可以看出，再选科目单科与必考科目语数外总分之间相关系数r 的取值在[0.63-0.84]，这说明使用语数外总分去校准再选科目成绩是合适的，再选科目成绩与必考科目成绩之间有着正相关联系和规律：某个再选科目考生群体的整体水平（语数外总分）越高，该科目的整体成绩也会越好。

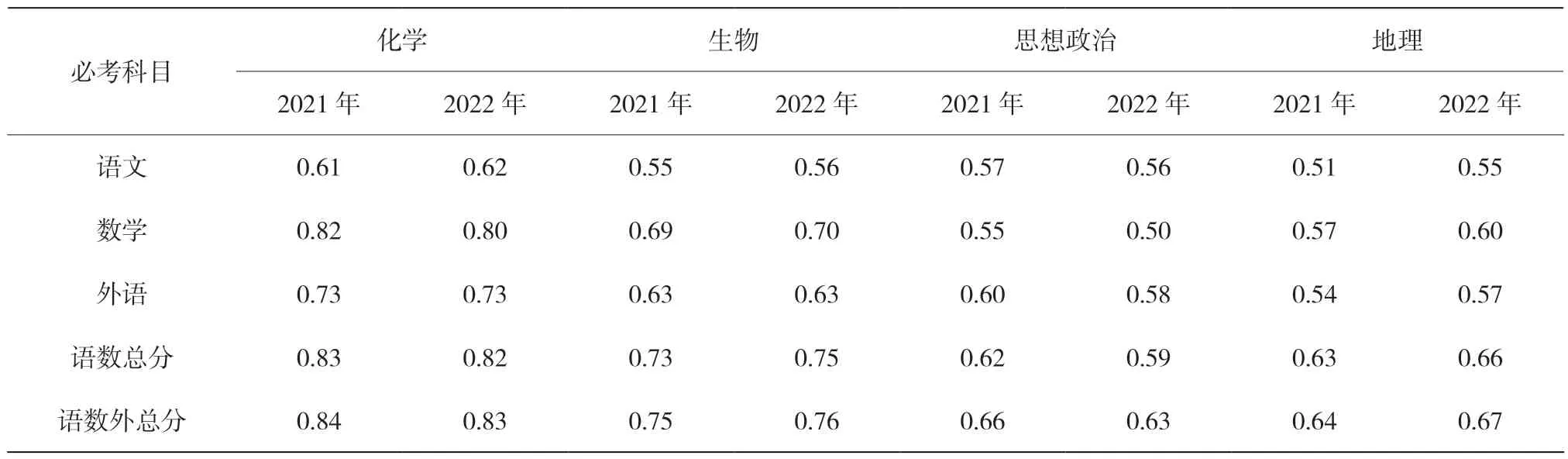
表1 再选科目与必考科目相关系数表

另外，笔者建议采用以语数外总分为参照对现有计分方式进行校准而不采用单科（或语文，或数学，或外语）校准，理由有两个：第一，根据加德纳多元理论，必考单科考查的能力有限，只用某个单科来校准再选科目的话，其校准效度不如语数外总分；第二，表1 数据显示，再选科目与语数外总分的相关度明显大于其与语数外单科的相关度。

四、保障机制的仿真研究

不管哪种等级赋分校准方案，其最终目的都是借助某种参照，将赋分策略与选考科目考生群体的实际能力分布建立联系，通过校准使赋分结果更贴近考生与考生群体的真实能力水平。校准方案恰好可以作为再选科目保障机制的有益补充，使保障机制的修正策略不仅基于选考人数，也能更贴近选考考生群体实际能力水平的分布。通过前文几种校准方案的分析与比较，以语数外总分为参照的校准方案，具有更强的科学性、有效性和可行性。目前该方案尚停留在理论研究阶段，并无实证数据验证。为了比较再选科目现有等级赋分方案、保障机制方案、以语数外为参照的校准方案之间的差异和优劣，考察验证保障机制和校准方案的有效性，本文特进行模拟数据演算。

（一）模拟数据准备

笔者参照某年江苏高考数据用计算机模拟了5 万条数据作为全体考生数据（详见表2），模拟数据中1 万名优秀考生群体选考化学，2 万名次优考生群体选考生物，3 万名普通水平考生群体选择地理，4 万名较差考生群体选考思想政治。这里的优秀考生群体指的是语数外总分均值较高的选考科目考生群体，较差考生群体指的是语数外总分均值较低的选考科目考生群体。之所以这样模拟考生数据，一方面是为了体现出不同科目选考群体水平的差异性，另一方面将化学选考比例设置成20%，以模拟启动化学保障机制，对保障机制启动后的效果进行仿真研究。本文重点研究化学科目考生在三种赋分方案下的差异。

表2 全体考生模拟数据表

（二）现有赋分方式演算

再选科目现有等级赋分方式计算过程：

步骤1，划分等级、分配比例。按化学原始分从高到低排序，将化学科目考生划为A、B、C、D、E 五等，等级比例取值A-15%，B-35%，C-35%，D-13%，E-2%。

步骤2，计算等级人数、切分考生。根据等级比例计算出每个等级对应的考生人数，按照每个等级的考生人数切分考生数据。因为等级边界通常会存在同分考生，所以此时切分出的各等级考生人数并非最终实际人数，需要进行微调。

步骤3，同分微调。对于边界同分考生，依据同分考生必须划分到同一等级的原则，采用“就高不就低”的微调方法，将每个等级的下边界同分考生都划到该等级。经过微调后的考生人数才是各等级的实际人数。

步骤4，考生赋分。依据等比例转换法则，计算每个考生的等级分。等比例转换计算方法参见公式2，其中t1、t2代表某个等级的上、下边界等级分，x1、x2代表相应等级的上、下边界原始分，x 代表该等级某个考生的原始分，t 代表转换后的相应等级分。在未启用保障机制情况下，根据现有等级计分方式计算过程，得到化学考生等级赋分数据表（详见表3）。

表3 化学考生数据表—现有等级赋分方式

依据江苏省再选科目保障机制规则，模拟考生数据中化学选考人数比例为20%，因而需要启用化学保障机制。启用保障机制后，其计算过程和上述步骤一样，只是要将化学科目考生人数用保障基数代替，保障基数=全体考生人数*保障比例（即：50000*25%=12500）。在启用保障机制的情况下，经计算得到等级赋分结果参见表4。

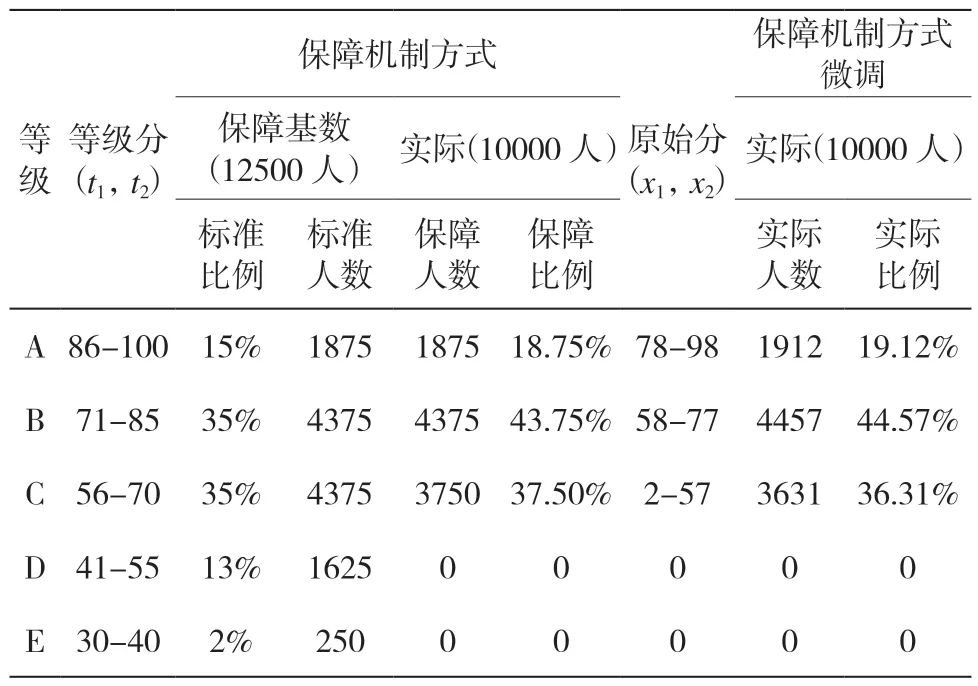
表4 化学考生数据表—保障机制方式

（三）语数外总分校准方式演算

参考前文校准方案思路对以语数外总分为参照的校准方式进行细化，细化后的校准方式计算过程分为三个阶段：

第一阶段，对全体考生数据进行切分：

步骤1，首先将全体考生按语数外总分从高到低排序。

步骤2，对全体考生进行等级划分，划分成A、B、C、D、E 五个等级，等级比例取值：A-15%，B-35%，C-35%，D-13%，E-2%，即标准比例。根据全体考生人数和各等级标准比例，计算出各等级标准人数，同时记录每个等级下边界的标准累计排位名次。

步骤3，把每个等级下边界排位名次考生（该等级最后一名考生）的语数外总分作为等级下边界分S2。每个等级的下边界分确定后，次一级等级的上边界分S1同时也被确定下来。

步骤4，重复步骤3，记录每个等级的上下边界分（语数外总分S1、S2）。

第二阶段，对再选科目考生数据进行切分：

步骤1，对再选科目进行等级划分，同样划分成A、B、C、D、E 五个等级，五个等级对应的等级分区间：A[86-100]，B[71-85]，C[56-70]，D[41-55]，E[30-40]。各等级人数及比例待定。

步骤2，根据第一阶段得到的各等级上下边界分（语数外总分S1、S2），去统计每个再选科目（化学、生物、思想政治、地理）考生群体中语数外总分符合对应等级要求的考生人数。

步骤3，根据统计出来的各等级人数，计算出每个再选科目相应等级的考生人数比例，这个比例大概率与标准比例不同，这里的人数、比例信息就体现出不同再选科目考生群体水平的差异性。由于边界考生同分的问题，这里计算出的考生人数、考生比例并不是最终切分的实际人数、比例，需要进行微调。

步骤4，将再选科目原始分（比如，化学科目用化学原始分，生物科目用生物原始分）从高到低进行排序，根据步骤3 计算出的各等级的考生人数找到每个等级的上下边界分（再选科目原始分x1、x2），对于边界同分考生，依据同分考生必须划分到同一等级的原则，采用“就高不就低”的调整办法，将每个等级的下边界同分考生都划到该等级。如此计算得到的各等级的考生人数和比例才是最终切分后各等级的实际考生人数和比例。

第三阶段，对再选科目考生赋分：

根据第二阶段切分考生数据后得到各等级的上下边界分（再选科目原始分x1、x2），对照相应等级既定的上下边界等级分（t1、t2），使用等比例公式（参见公式2）计算出每个考生的转换分t，即校准等级分。

以语数外总分为参照校准再选科目等级分的方案关键之处有两点：其一，统计每个再选科目（化学、生物、思想政治、地理）考生群体中语数外总分符合对应等级要求的考生人数；其二，依据此人数去定位相应等级的再选科目原始分，然后根据各等级的边界分（再选科目原始分x1、x2）去调整再选科目人数。使用细化后的校准方式对考生数据进行演算，结果参见数据表5。

表5 化学考生数据表—校准方式

（四）三种方式比较

笔者将三种赋分方案下化学科目考生的等级划分和计算结果放在一起形成表6，对数据进行对比分析后，得出以下两点结论：

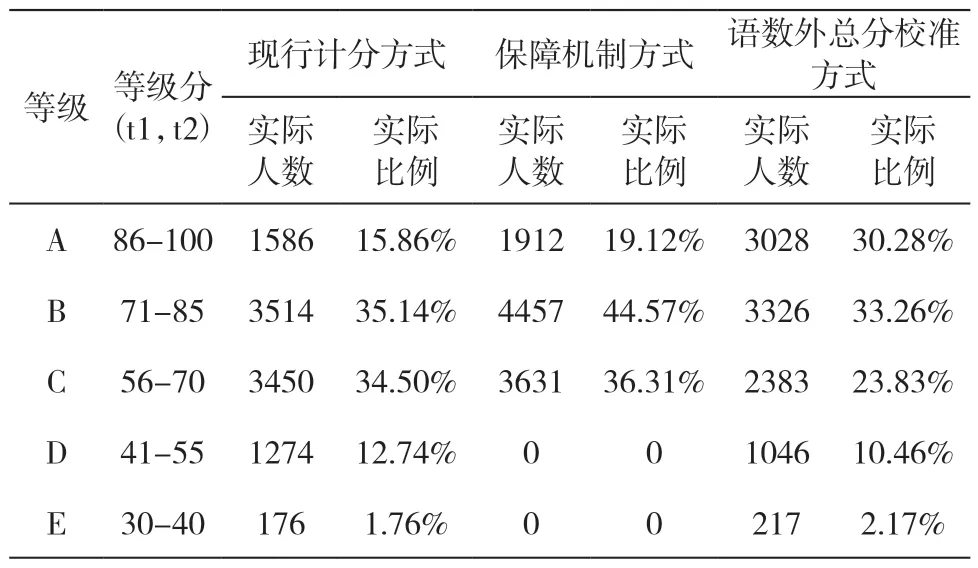
表6 化学考生数据表—三种方案对比

第一，比较现有等级赋分方式与保障机制方式，以现有计分方式为参照，考察启用保障机制前后考生等级变化情况。经过保障机制方式调整，化学科目考生受益群体：E 等级176 人（100%），D 等级1274 人（100%），C 等级考生1269 人（36.78%），B 等级考生326人（9.27%）。根据模拟数据演算结果，在化学保障机制方式下，E、D 等级所有考生都升级至C 级，C 级有很多考生（36.78%）升级至B级，B级只有少数考生（9.27%）升级至A 级。这说明保障机制对低水平考生保障力度要高于对高水平考生的保障力度，江苏再选科目保障机制可以从加大对高水平考生保障力度的角度进行优化和完善。

第二，比较现有等级赋分方式与语数外总分校准方式，以现有计分方式为参照，考察以语数外总分进行校准前后考生等级变化情况。经过校准后，化学科目受损群体：D 等级考生41 人（3.22%）；受益群体：D 等级考生187 人（14.68%），C 等级考生1254 人（36.35%），B 等级考生1442 人（41.04%）。仿真结果显示，在以语数外总分为参照的校准方式下，中高水平考生群体受益面积很大（C 等级考生36.35%升级至B 等级，B 等级考生41.04%升级至A 等级）。说明该校准方式有利于优等生报考的科目，可以提高高分段考生的等级赋分，这恰好可以作为保障机制的有益补充，引导中高水平考生积极报考难度较大、优等生相对集中而总报考人数较少的化学科目，而这也正是保障机制政策的初衷之所在。

（五）其他科目数据仿真

笔者使用现有赋分方式与以语数外总分为参照的校准方式对其他三门再选科目（生物、思想政治、地理）进行数据仿真演算，得到数据表7。

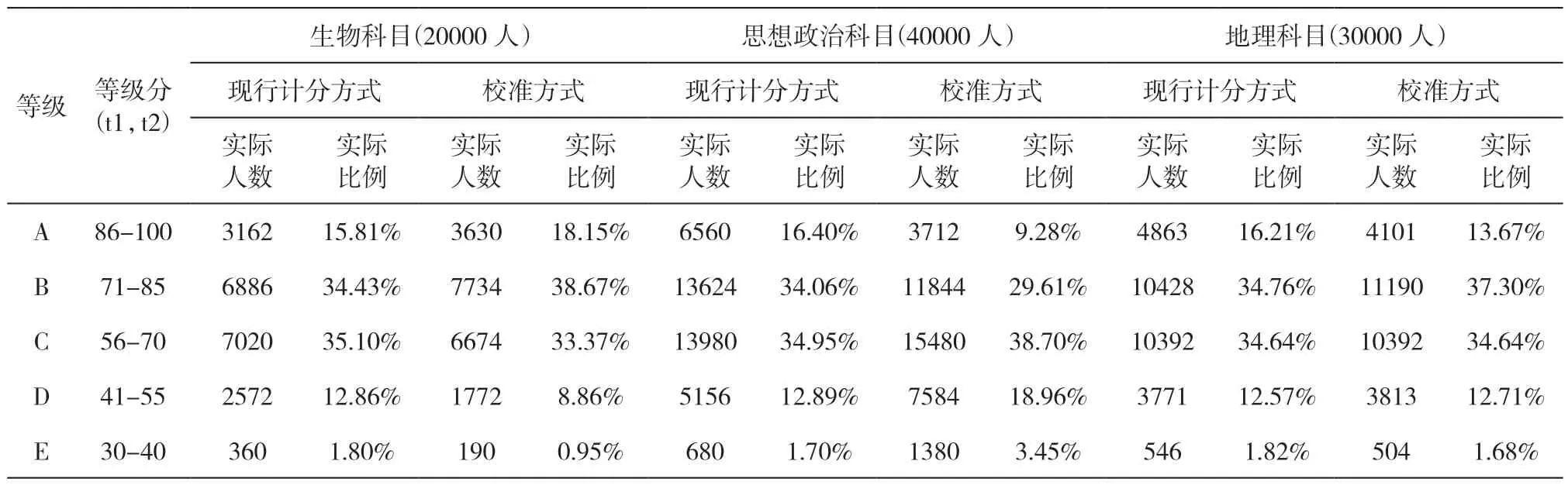
表7 其他三门科目赋分方式对比表

分析数据表7，以现有计分方式为参照，考察以语数外总分进行校准前后考生等级变化情况，得到以下结果：

1.经校准后，生物科目受益群体：E 等级考生170人（47.22%），D 等级考生970 人（37.31%），C 等级考生1316 人（18.75%），B 等级考生468 人（6.8%）。

2.经校准后，思想政治科目受损群体：D 等级考生700 人（13.58%），C 等级考生3128 人（22.37%），B 等级考生4628 人（33.97%），A 等级考生2848 人（43.41%）。

3.经校准后，地理科目受损群体：A 等级考生762人（15.67%）；受益群体：E 等级考生42 人（7.7%）。

根据模拟仿真结果，以语数外总分为参照进行校准后显示：生物科目所有等级考生都出现升级情况，其中E、D 等级考生升级比例很大（E 等级47.22%，D 等级37.31%），B 等级考生升级比例偏小（6.8%）；思想政治科目与生物科目相反，所有等级考生均出现降级情况，其中中上成绩考生降级比例最大（A 等级43.41%，B 等级33.79%）；地理科目A 等级少部分考生降至B等级（15.67%），E等级少部分考生升级至D等级（7.7%）。仿真结果显示，以语数外为参照的校准方式有利于生物科目考生，不利于思想政治科目考生。

通过四门再选科目各等级考生比例校准前后对比图（详见图1、图2），结合再选科目语数外总分均值表（详见表2）可以看出，校准后再选科目各等级的考生比例趋于合理，更符合各科目考生群体的实际水平层次，可以说，校准前是形式上的公平合理，校准后是实质上的公平合理。

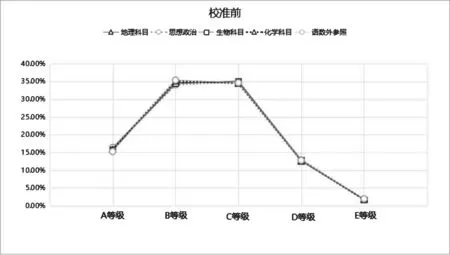
图1 再选科目各等级考生比例图-校准前

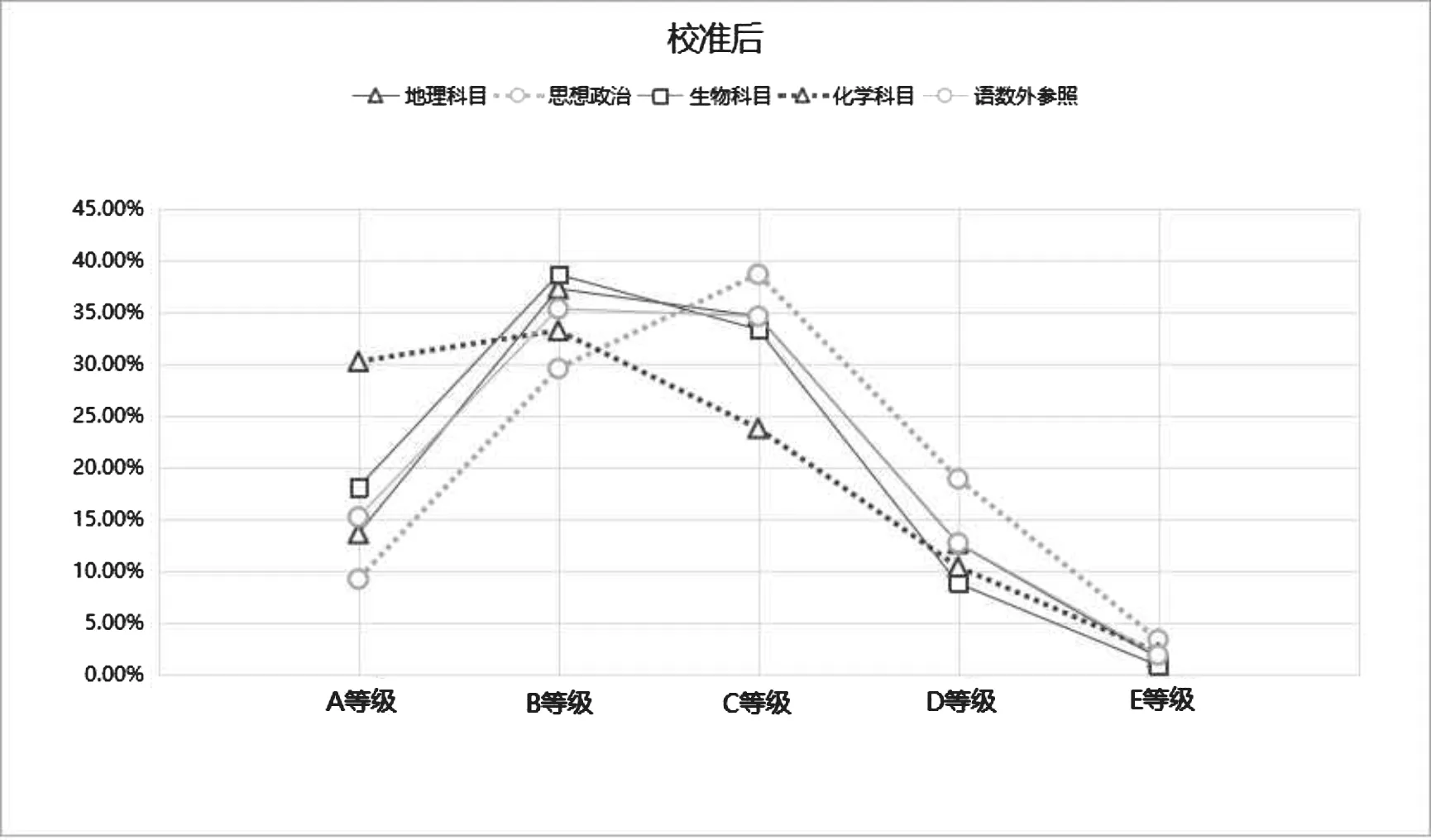
图2 再选科目各等级考生比例图-校准后

五、结语

新高考改革中的等级赋分方案初衷是为了实现选考科目间的可比可加，但这个设计有其内在缺陷，它在试图摆平各科难度差异的同时也抹平了选考群体能力差异，所以转换效果出现偏离，从而引发了考生功利性选科的现象发生。本文模拟仿真结果表明，江苏保障机制方式在引导考生正确选科方面起到了积极的作用，但其对低水平考生的保障力度要大于对高水平考生的保障力度，仍有进一步优化和改进的空间；以语数外总分为参照的校准方式可以作为保障机制的有效补充，校准后的等级转换分更贴近考生在群体中的真实水平层次，但该校准方式计算过程较为繁琐，且有不足之处，比如语数外加权分数校准是否比语数外总分校准更加合理等，需要进一步研究和验证。

综合考量学术研究与实践操作，由于语数外总分校准方式只是一种模拟尝试，且计算过程较为繁琐，大众理解方面也有待考量，而江苏再选科目保障机制方式形式简单、大众易于理解，且有实际数据支撑，在引导学生正确选科方面起到了积极的作用，建议目前仍使用保障机制方式，但不要放弃优化改进的空间，积极探索进一步优化改进和完善的办法。