整体化归思想在初中数学解题中的妙用

肖 凡

(三明市第八中学,福建 三明 365000)

初中数学是培养学生逻辑思维能力和解决问题能力的重要阶段.在解题中,一些思想方法的应用,能够帮助学生更好地理解和解决各类数学问题,而整体化归思想就是其中一种重要的思想方法[1].本文旨在探讨整体化归思想在初中数学解题中的妙用,通过具体例题的分析和研究,总结出整体化归思想在简化计算、提高解题速度和解题正确率等方面的作用,以期为初中数学解题教学提供一些有益的思路和方法.

1 化简代数式类问题

整体化归思想在代数式的化简中有着重要的应用.通过将代数式看作一个整体,我们可以更好地理解这个整体与已知量之间的关系,从而更加灵活地运用各种代数技巧,如合并同类项、提取公因式、配方等,将复杂的代数式化简为更加简单的形式[2].这种思想可以大大简化计算过程,提高解题效率.

利用整体化归思想化简代数式主要包含以下几个步骤:首先,分析代数式结构,观察代数式的特点,将其分解成多个部分,并确定各部分之间的关系.其次,提取公因式或“已知条件整式”(已知条件中给出的整式,一般会给出该整式的具体值或代数值,如整式2x2+3y=5,或2x2+3y=a),将代数式中的公因式提取出来,以简化代数式.然后通过变形和化简,将代数式转化为更加简单和易于计算的形式,计算过程中可以通过各种代数技巧,如乘法分配律、结合律等来实现[3].最后,将代数式中的各项进行运算和化简,得出化简后的结果.

整体化归思想在代数式的化简中有着广泛的应用,它可以帮助学生更加灵活地运用各种代数技巧,提高解题速度和准确率.同时,这种思想也可以培养学生的思维能力和创新能力,帮助他们更好地解决各种数学问题.

例1 提示“用整体思想解题:为了简化问题,我们往往把一个式子看成一个数(整体).”试按提示解答下面问题.

(1)若代数式2x2+3y的值为-5,求代数式6x2+9y+8的值.

(2)已知A+B=3x2-5x+1,A-C=-2x+3x2-5,求当x=2时B+C的值.

解析(1)设m=2x2+3y=-5,所以6x2+9y+8=3m+8=3×(-5)+8=-7,即所求式的值为-7.

(2)由已知条件,可以进行整体配凑B+C=(A+B)-(A-C).

代入已知条件得到(3x2-5x+1)-(-2x+3x2-5)=-3x+6=-3×2+6=0,因此,当x=2时,B+C=0.

点评整体化归思想可以帮助学生将复杂的代数式或几何问题简化,从而更容易地找到问题的答案.本题难度略低,是一道培养整体思想在初中数学解题中应用的题目.先给出整体化归思想的条件,奠定解题思路,然后由易到难设计两个题目进行整体化归思想的锻炼.可根据已知条件直接进行整式配凑,最后将整式具体值代入配凑好的部分进行“整式消去”,从而得到最终答案.

2 解方程类问题

在解方程时,有时直接入手比较困难,这时可以使用整体化归的思想.将方程的某部分看作一个整体,通过转化和变形,便可以将这个整体用已知量表示出来.整体化归的思想在解决方程问题时非常重要,通过将方程的解看作一个整体,我们可以更好地理解方程的解和已知量之间的关系[4].这种思想可以帮助我们更加灵活地运用方程的变形和化简方法,从而更容易找到方程的解.同时,整体化归的思想也可以培养我们的数学思维和解决问题的能力,使我们能够更好地应对各种复杂的数学问题.

第二问中:

在方法一中,通过利用第一问的结论,将x+y,x-y看作整体,使用整体化归思想解题,大大简化了计算过程.

方法二同样是利用整体化归的思想,只是没有结合第一问的结论.该方法较方法一稍显复杂,但该方法是整体化归思想的通用思想,可以推广使用.

方法三整理原方程组,

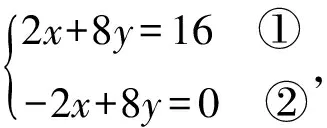
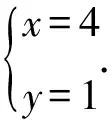
方法三没有用整体化归的思想,在计算方面考查细致度,计算过程需要精确拆括号,变换正负号.

点评本题考查了二元一次方程组的解法,解二元一次方程组的基本思想是消元,加减消元法和代入消元法是常用的方法.运用整体思想,把第二问中的方程组转化成第一问的方程组,简化了计算.方法三没有明显地运用整体化归的思想,而是更注重于计算方面的考查.在具体操作中,需要精确地拆括号和变换正负号,这需要一定的细心和耐心.比较这三种解法,我们可以发现方法一最为简单,方法二次之,而方法三则相对较为繁琐.整体化归思想在数学中有着广泛的应用,它可以帮助我们将复杂的问题化整为零,将未知转化为已知,从而使问题更易于解决.从这三种解法中,我们可以看出方法一和方法二都运用了整体化归的思想,将问题进行了整体把握和转化,从而使问题的解决更为简洁和高效.因此,在数学学习中,要注重培养自己的整体化归思想,学会将问题进行整体把握和转化,从而更好地解决数学问题.同时,也需要注重计算的训练和提高,以更好地运用整体化归思想来解决数学问题.

令①-②,得x2-3xy+4y2=11.所以x2+xy+4y2=11+4xy,所以,把xy=2代入得x2+4y2+xy=11+8=19,即整式x2+4y2+xy的值为19.

点评本题考查了整体化归思想的应用,这种方法在处理复杂问题时具有很大的优势,可以大大简化计算过程,提高解题速度和正确率.对于问题一,由于已知条件和所求结果之间存在明显的整体代入关系,因此只需要直接将所给的整体代入到结果中即可求出答案.对于问题二,需要先将原式进行适当的整理和变形,找出已知条件中的某些量的关系,并将它们分别代入到计算公式中.在进行整体代入时,需要注意两点:首先,要认真分析问题中各个量之间的关系,确定哪些量是相互独立的,哪些量之间存在某种比例关系;其次,在将已知条件中的式子进行“配凑”时,要尽可能地使代入后的式子保持对称性或规律性,以便于计算和分析.因此,整体化归思想在初中数学解题中具有广泛的应用价值,通过培养学生的整体化归意识,可以提高学生的解题能力和数学素养.